基于Jackson模型的高频海底散射研究

杨玉春

(声纳技术重点实验室 第七一五研究所，杭州，310023)

基于Jackson模型的高频海底散射研究

杨玉春

(声纳技术重点实验室 第七一五研究所，杭州，310023)

高频海底声散射是一个非常复杂而重要的过程，根据海底散射强度可以进行海底底质参数估计和识别分类等，因此一个合理的高频海底散射模型有非常重要的理论意义和工程价值。文章以Jackson散射模型为基础，将海底散射分为界面散射和体积散射两部分，定量研究了高频海底散射强度的空间分布特性，为某些海底图像声呐（如侧扫声呐、多波束测深声呐等）的应用奠定了良好基础。

Jackson模型；海底散射；散射空间分布；底质参数

为了更好的研究和分析海底特性，高频海底声散射一直以来受到高度关注，国内外学者也提出了各种各样的散射模型。例如Dale D Ellis等人结合Lambert法则和Kirchhoff近似理论得到一个三维散射函数，并用此函数计算收发分置混响；彭朝晖等人结合Ιvakin等的射线管积分法和Hines的最速下降法，提出了一个计算随机非均匀海底和海底粗糙界面引起的平面内海底散射模型。1986年Jackson等人提出了一种应用复合粗糙模型的高频海底散射模型（简称Jackson模型），Steve Stanic等人将试验测得的数据结果与多个散射模型进行比较分析，认为此模型计算的结果在不同条件下都能更加合理地反映真实数据。本文以Jackson模型为基础，对高频海底散射进行理论建模，模型包含散射强度与入射声波频率、声波掠射角、海底环境参数等一系列参数，它将海底散射分为粗糙海底界面散射和海底沉积物体积散射。

1 高频海底散射模型

由于高频声波穿透海底能力不强，因此将体积散射等效为薄层界面散射，并引用Urick给出的定义，将散射强度定义为其中，分别是界面散射截面和体积散射等效散射截面。

1.1 海底界面散射

该模型中假定海底界面起伏为各向同性、二维的高斯随机过程，海底沉积物为流体状态，不考虑其弹性、粘滞性、沉积物分层的影响。该模型引入二维高度谱的概念对界面的不平整性进行描述。

式中，W(k)为界面的二维高度谱密度，H(r)为高度随机分布函数h(r)的自相关函数。

在高度分布为各向同性高斯随机过程的假设前提下可求得二维高度谱密度的表达式为

式中k是二维矢量波数，w2和2γ分别为二维海底界面的谱强度和谱指数，谱指数的取值范围是，h0是参考长度，通常取值为h0=1 cm。

海底界面散射示意图如图1所示，为了计算方便，建立坐标系时，令入射波矢量方位角。

图1 海底散射示意图

分别将入射波矢量和散射波矢量分成两个部分

影响海底界面散射强度的因素很多，例如海底粗糙度、声波掠射角、入射声波频率等，国内外学者提出了许多不同的方法来计算海底界面散射强度，其中Kirchhoff近似法和微扰近似法是两种较为经典的方法，本文将采用这两种方法分别对海底界面散射进行计算。

1）Kirchhoff近似法

Kirchhoff近似方法适合海底较为光滑（粗糙度较小）、且掠射角较大的情形，原则上界面每一点处的曲率半径Rc需满足如下条件：

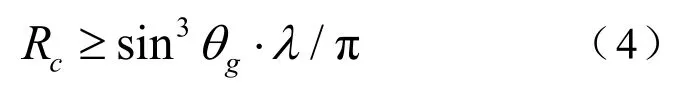
其中gθ是声波掠射角，λ是入射声波波长。当声波的波长和界面曲率半径固定不变时，随着掠射角的减小，Kirchhoff近似的适用性也逐渐变差。

Jackson在模型中还引入了两个所谓的“结构函数”参数：

按照Kirchhoff近似方法，其散射截面可写为

式（7）中相关参数说明如下：

其中ρ是海底沉积物密度与海水密度之比，v是沉积物中声速和海水声速之比，δ是沉积物中波矢量的虚部和实部之比，J0(⋅)为零阶贝塞尔函数。

在高频近似下，（7）式中的积分部分可作近似计算，简化为

2）微扰近似法

微扰法近似适合声波掠射角较小的情形，经过一系列复杂的推导[2]，其海底界面散射强度可写为：

Kirchhoff近似法和微扰近似法在计算海底界面散射强度方面各有优势，但也有不足之处：Kirchhoff近似法在小掠射角部分计算出的散射强度并不准确；而微扰法在大掠射角部分计算出的散射强度不准确。

取如下一组典型的海底环境参数ρ=1.87，v=1.126，δ=0.016 6，γ2=3.67，w2=0.004 42。在入射声波的频率f=20 kHz，分别用Kirchhoff近似法和微扰法计算出的海底界面反向散射强度变化。

图2 海底界面反向散射强度随掠射角的变化

综上所述，在掠射角为0°～90°的变化范围内，为了得到较准确的海底散射强度，需要将两种近似法进行很好的融合。方便可靠的方法是将Kirchhoff近似法和微扰法计算出的结果进行内插而得到总的界面散射截面，其内插形式如下：

其中η为插值系数，一般取η=-2。

1.2 沉积物体积散射

在体积散射中，需要用三个参数来描述沉积层中的密度不均匀性和可压缩程度：密度不均匀性谱密度Wρρ、可压缩性谱密度Wkk和两者的交叉谱密度Wkρ。

类似于二维海底界面高度谱密度，沉积层密度不均匀性可用三维、各向同性的密度谱来描述：

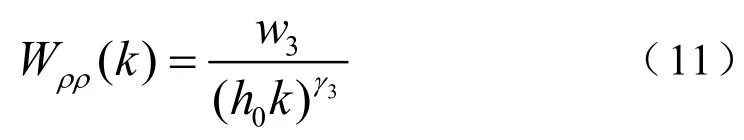
其中，w3和3γ分别为体积谱强度和谱指数。可压缩性谱密度为

其中，μ是海底沉积物密度扰动的可压缩比。

密度不均匀性和可压缩性的交叉谱为

与前面类似，在沉积物中，入射声波波矢量可写为

同理，散射波矢量

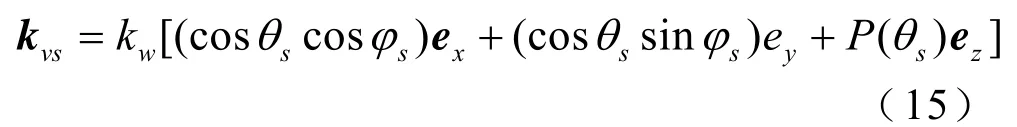
从而可推得

经过一系列的近似和化简，体积散射等效散射截面最终可写为：

取如下一组典型的海底环境参数：ρ=1.87，v=1.126，δ=0.016 6，γ2=3.67，w2=0.004 42，γ3=3，w3=1.27×10-4，μ=-1。同样在入射声波的频率f=20 kHz时，计算出海底界面散射强度和沉积物散射强度见图3。图中反向界面散射强度是经过Kirchhoff近似法和微扰近似法分别计算出结果按照（10）式进行内插产生的。从图中可以看出，虽然声波频率很高，但沉积物体积散射依然不能忽略，在掠射角较小时，沉积物反向散射强度随掠射角的增大而迅速增大，但超过临界角后，便没有太大变化，基本维持在一个固定值，当然这个值的大小是由海底沉积物参数决定的。

图3 海底界面散射和体积散射强度

图4是海试时利用某侧扫声呐采集到的反向散射回波数据计算出的海底反向散射强度。从图中可以看出，根据侧扫声呐接收到的回波计算出的海底反向散射强度，与根据Jackson模型算出的理论值总体上吻合得较好，同时可以反演出海底可能是细沙和淤泥的混合海底。

图4 实测值与Jackson模型理论值比较

2 海底散射强度的空间分布

前面推导了海底界面散射和沉积物散射强度的表达式，并对海底反向散射强度进行了一些计算和仿真，也通过海试实验数据验证了该散射模型的正确性。下面主要是对海底散射强度的空间分布做一些仿真计算，也就是在某个入射角情形下，不同掠射角方向上的散射强度分布，当然这里主要研究的是入射声线与散射声线在同一平面内的情形，这也是实际工程中最为关注的。

同前面一样，在入射声波的频率f=20 kHz时，取如下一组典型的海底环境参数进行计算：ρ=1.87，v=1.126，δ=0.016 6，γ2=3.67，w2=0.004 42，γ3=3，w3=1.27×10-4，μ=-1。

图5 海底散射强度的空间分布仿真

从图5中可以看出，在上述典型海底环境参数下，镜像反射方向附近的散射强度是最大的，为了表述方便，将这个散射强度最大的方向叫镜像散射方向。入射声波掠射角越小，散射能量越集中到镜像散射方向，随着掠射角增大，这种情形有所好转。从仿真计算结果来看，这是符合实际情况的。

3 结论

随着对海洋资源的开发和利用，海底地形地貌的测绘工作显得越来越重要，而利用高频声波的海底散射是研究海底特性的重要手段，因此建立一个合理的高频海底散射模型有非常重要的理论意义和工程价值。本文对基于Jackson散射模型进行了较为详细的研究，对其理论进行离散化数值仿真，还对海底反向散射强度用海试数据进行了验证，另外在掠射角为0°～180°方向范围内的散射强度进行了仿真计算，结果符合预期，具有较大的工程参考价值。

[1]JACKSON D R,ANDREW M,JOHN J.Highfrequency bottom backscatter measurements in shallow water [J].JASA,1986,80(4):1188-1199.

[2]JACKSON D R,KEVΙN B.High-frequency bottom backscattering:Roughness versus sediment volume scattering [J].JASA,1992,92(2):962-967.