多约束单历元的北斗双频高精度定向技术实现
2015-01-09旷野茅旭初
旷野 茅旭初
(上海交通大学电子信息与电气工程学院,上海,200240)
多约束单历元的北斗双频高精度定向技术实现
旷野 茅旭初
(上海交通大学电子信息与电气工程学院,上海,200240)
以双频宽巷组合为基础,利用最小二乘模糊度搜索算法并结合多约束条件缩小搜索范围,最后用比例检验法进行模糊度确认并用B1、B2双频检验确认基线向量。算法采用单历元,极大减小初始化时间。静态定向实验表明,该算法可以减少解算时间,提高精确度和稳定性。
北斗系统定向;双频;单历元;宽巷组合;多约束条件
全球卫星定位系统(GNSS)可以测定载体的航向,没有时间累积误差,广泛地应用于飞机、船舶航向测定以及火炮定向等领域。
GPS播发L1、L2两个频点的信号,L1频段上C/A码为民用码,L2频段上P码为军用码,对于一般用户无法获得P码,也就无法获得L2上的伪距观测值。目前GPS双频接收机主要利用载波相位技术实现测距,由于P码结构未知,L2载波重建时需要很复杂的算法来剥离测距码,且重建信号信噪比较低。北斗卫星导航系统播发的信号频率为B1、B2,两个频段上均发布民用信号,可以真正意义上独立接受B1、B2上的双频载波和测距码[1]。
目前定向技术大多采用载波相位方法,其关键是整周模糊度的求解与确定。主要解算方法有模糊度函数法(AMF)、快速模糊度求解方法(FARA)、快速模糊度搜索滤波方法(FASF)以及最小二乘模糊度去相关法(LAMBDA)等[2]。近些年S Jazaeri提出利用晶格理论来加快整周模糊度的搜索过程[3],胡丞铭提出直接固定准则来确定整周模糊度[4],Wantong Chen提出通过K-S检测、航向验证、模糊度函数全局最小等手段在单频接收机单历元下的定向方法[5]均取得较好的结果。但是存在初始化时间较长、运算量大等缺点,使用单历元解算可以很好地解决这些问题,但随之带来解算成功率不高、受周围环境影响较大等新问题需要进一步解决。
1 卫星定向基本原理
卫星定向一般采用双天线的方式,如图1,北斗B1和B2上的载波相位在传播的不同位置有不同的值,点O为发射信号的相位零点,点P距离点O半个波长,任何时刻点P滞后点O半个周期即180°,点Q相位滞后点O也是180°,两点之间的距离为(N+0.5)λ,N为一未知整数,在卫星定向领域叫做整周模糊度[6],接收机收到的载波相位实际上是卫星发出信号的相位与接收机产生的参考信号的相位差。

图1 双天线卫星定向图
双天线定向即确定接收机A与接收机B的相对位置,即二者在CGCS2000坐标系中构成的矢量,进而求得航向角和俯仰角。图1中的为接收机A到接收机B的位置矢量,为卫星i相对于接收机的单位方向矢量,接收机A对卫星i的观测方程为:
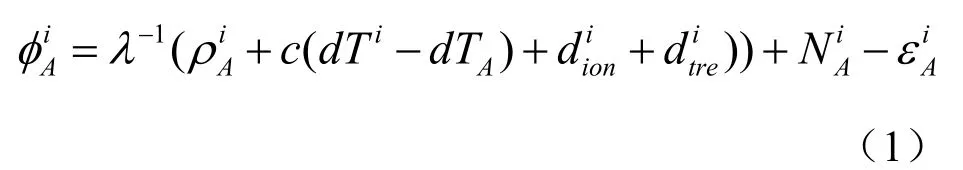
式(1)中λ为北斗B1载波频率(1 561.098 MHz)对应的波长,m;为接收机A观测到的卫星i载波相位;为接收机A到卫星i的真实距离,m;c为光速;idT为卫星i的时钟误差,s;dTA为接收机A的时钟误差,s;为卫星i到接收机A之间载波的整周数,即整周模糊度;为卫星i到接收机A的电离层延迟,m;为卫星i到接收机的对流层延迟,m;为卫星i到接收机A之间的其它未知误差,m。针对天线B也有同样的相位观测方程。式(1)中真正关键的只有与接收机位置信息相关的参量,其余各项误差参量实际上并不需要关心。在短基线条件下这些误差参量之间有着较好的相关性,可以通过差分运算将这些误差消除。
将接收机A和接收机B对卫星i的相位观测方程差分,由于主从接收机距离较近,电离层延迟误差、对流层延迟、卫星的时钟误差idT都可近似消去,得到单差方程:

定向的目的是要求出两个接收机天线之间的基线矢量,需要将基线矢量同单差载波相位测量值联系起来,由图1可以看出,接收机A和接收机B到卫星i的单差几何距离与基线矢量在观测方向上的投影相等,即

进而单差方程可以描述为:
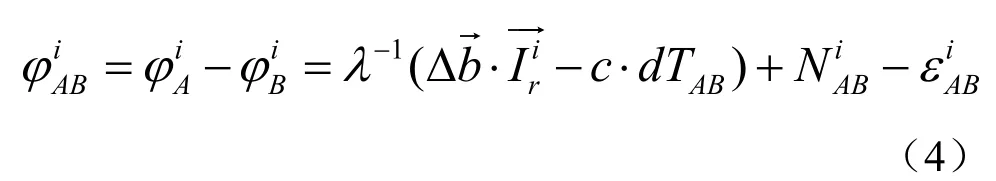
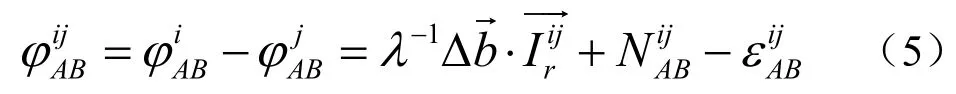

2 北斗双频单历元整周模糊度解算
整周模糊度的求解可分为单历元和多历元两种,多历元利用一段时间的观测值进行计算,收敛到全局最小值的概率较高,但是却也不可避免地存在解算时间长、周跳等问题。
基于最小二乘的模糊度求解是将某个目标函数最小化,使模糊度平方和最小,目前主要的解算方法有最小二乘模糊度搜索算法(LSAST)、快速模糊度求解方法(FARA)、优化Cholesky分解法以及最小二乘模糊度去相关法(LAMBDA)、零空间法等,本文通过对北斗B1、B2信号进行宽巷组合,利用伪距取整估算快速求解模糊度初值,并结合基线约束、俯仰角约束使用多约束条件下改进的最小二乘整周模糊度搜索算法,最后通过双频检验确定最终的整周模糊度。
2.1 模糊度的伪距取整估算法
若接收机A接收的卫星i的伪距测量值为,则伪距可表示为



其中[]代表取整运算,可见整周模糊度的估算精度与波长λ相关,增大λ可以缩小搜索范围,提高搜索速度和精度。
2.2 北斗双频宽巷组合
北斗B1Ι信号标称载波频率为1 561.098 MHz,B2Ι信号标称载波频率1 207.140 MHz,根据c=λf可得对应的波长分别为19.22 cm和24.85 cm[7]。
若1φ、2φ为某个卫星发射的载波相位观测值,f1、f2为对应的载波频率,信号传播时间为τ,则有
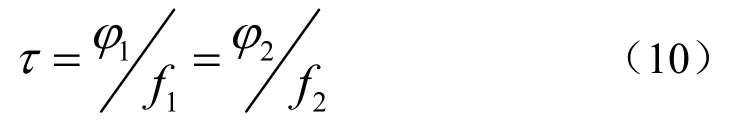
一般而言的双频观测组合可以表示为
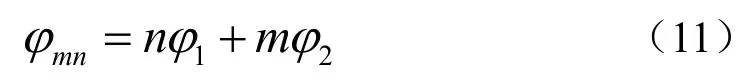
宽巷组合也应该满足式(10),即

组合后的波长λmn满足
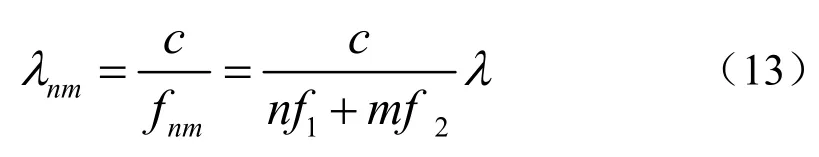
由式(9)和式(13)可得

当n=1、m=1时称为窄巷组合;n=1、m=-1时称为宽巷组合;n=1、m=0时即为BDS单频定向[8]。各种频率组合的频率和波长如表1所示。

表1 常见双频组合
宽巷组合具有较长的波长和非常小的载波方差,有利于模糊度的求解,但是放大了测量噪声,窄巷组合具有较小的距离方差,有利于基线矢量的精度,但是波长短,载波方差较大,不利于模糊度的求解。
本文采用宽巷技术,缩小模糊度搜索的空间,更快速更准确的确定模糊度。由于宽巷组合基线矢量精度不高,利用所得结果重新对B1、B2进行模糊度确认,得到更加精确的基线矢量。
2.3 模糊度最小二乘搜索算法
最小二乘模糊度搜索算法LSAST基于模糊度残差平方和最小原则,最早由Hatch提出[9],其基本思想是只要求出三个双差整周模糊度,就可以确定基线矢量,再由基线矢量分别求得其他双差整周模糊度。初始的三个双差整周模糊度可以用伪距取整算法求出。该方法需要将卫星分为两组,选择四个作为主星,其余为冗余星,这样将搜索的维度由M-1降至3,大大提高了搜索效率。选择主星的标准是几何精度因子GDOP,它反映了卫星分布状况
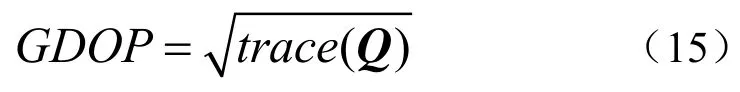
实验中一般选择最小GDOP对应的四颗星为主星,同时结合卫星俯仰角及信噪比的要求。四个主星的双差方程为
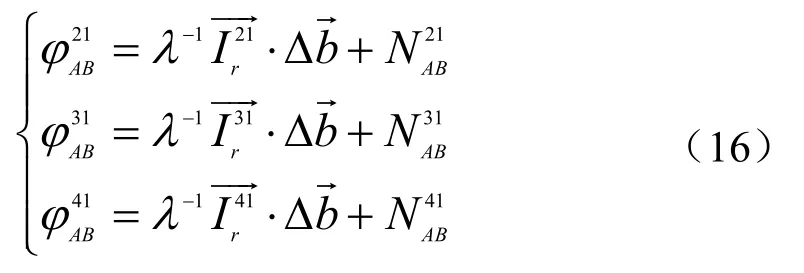
利用式(16)求出初始基线矢量,再将其代入冗余星方程,搜索其他模糊度
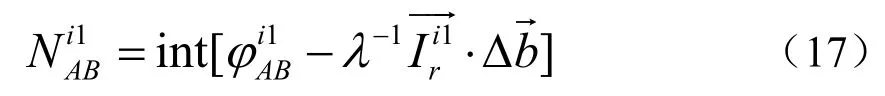
相位模糊度的方差为:

式中pδ、φδ分别为双差载波相位和伪距测量噪声的方差,m。设N1为距离估算的实数解最近的整数,则在置信度为1-ζ的范围内,模糊度N的取值取值空间为

2.4 基线约束和俯仰角约束
利用事先测量好的基线俯仰角和基线长度,可以去除与之不相符的整周模糊度,缩小模糊度搜索范围,提高效率和成功率。将式(16)展开,可得

式中a和Δb分别是的分量,DDN和DDφ分别是双差整周模糊度和双差载波相位,将其表示为矩阵形式

对该方程取平方:
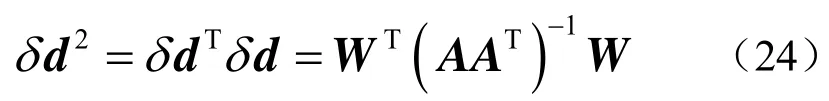
利用Cholesky分解,可将其表示为一个下三角阵及其转置的乘积,即,则


进而,


由已知基线的俯仰角,将双差整周模糊度带入下式判断其是否合理。

其中θ为事先所测基线俯仰角,δθ为允许的基线俯仰角误差。
通过对俯仰角与基线长度的约束,进一步缩小了双差模糊度的搜索范围。
2.5 模糊度确认
模糊度确认是模糊度全部求解过程的最后一步,它从搜索获取的可能集合中选取最优的值。理论上讲,模糊度确认至今还未完全解决,它的最大困难在于难以对各种误差进行准确建模。最为常见的检验方法是比例检验方法,它的基本思想是比较最小残差的平法和与次小残差的平方和,即,其中是最小残差的平方和,是次小残差的平方和,的取值非常关键,条件过宽会导致整个过程的求解时间延长,太严格可能将正确的模糊度排除在外[8],参考文献[10]中建议取为2。残差计算公式为

2.6 双频确认
在宽巷计算完成后回到B1、B2双频计算,得到B1小于阈值的双差整周模糊度组合和对应的基线向量,同理对B2也有小于阈值的双差整周模糊度组合和对应的基线向量,从基线矢量中选取相同的组合得到双频接收机的最终基线向量。将得到的基线向量结果从CGCS2000坐标系转换为北天东坐标系(O-NUE),

其中,Llat、Llon分别为接收机所在地理位置的纬度、经度,xN、yU、zE分别为O-NUE坐标系下的北向分量、天向分量和东向分量。进而计算两个接收机所成方向的航向角和俯仰角φ:

3 实验结果分析
本实验使用NovAtel OEM628接收机,它可以接收到目前所有GNSS系统的卫星信号,包括北斗系统B1、B2信号。单点定位精度单频时为1.5 m,双频时为1.2 m。GPS系统和BDS系统的C/A码和载波相位精度指标如表2所示。
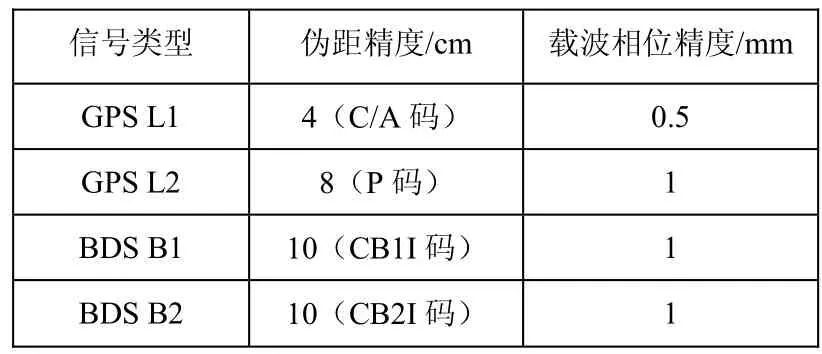
表2 信号精度比较
参考基准选择Hemisphere公司SDΙCOMPASS,它是一个GPS定向产品,使用双天线进行方向测量,同时内部集成了倾角传感器和陀螺仪,可静态及动态地测量各种角度,其航向角定向技术指标为:0.5 m 基线时0.25°rms,1 m 基线时0.15° rms,2 m 基线时0.1°rms;俯仰/横滚精度<1°rms。实验使用SDΙ-COMPASS测量24 h航向角取平均值作为参考航向角。
实验地点选在上海交通大学电子信息与电气工程学院二号楼楼顶,无建筑遮挡。基线长度分别为1.5 m、2 m、2.5 m,比较了各种情况下的定向精度。
3.1 北斗双频确认结果与北斗宽巷结果对比
在2 m基线下按照上述算法计算BDS双频宽巷组合直接解算的航向角以及经B1、B2双频确认后的航向角,对比如图2所示。

图2 2 m基线BDS双频确认航向角与宽巷直接解算航向角对比
可见单纯使用宽巷组合容易使整周模糊度在局部收敛,导致航向角偏差较大、鲁棒性差,经过B1/B2双频后精确度和鲁棒性都得到大幅提高
3.2 北斗双频确认结果与GPS双频确认结果对比
在2 m基线下比较BDS双频确认后的航向角和使用GPS双频解算的航向角,如图3所示。

图3 2 m基线BDS双频确认航向角与GPS双频解算航向角对比
可见BDS的精确度与GPS非常接近,由于BDS测距码精度和载波相位精度都略低于GPS,故可认为已达到较好的精确度指标。
3.3 北斗双频确认结果与北斗单频结果对比
在1.5 m、2 m和2.5 m基线下,分别比较BDS双频确认的航向角和BDS单频解算的航向角,如图4、图5、图6所示。

图4 1.5 m基线BDS双频确认航向角与BDS单频解算航向角对比
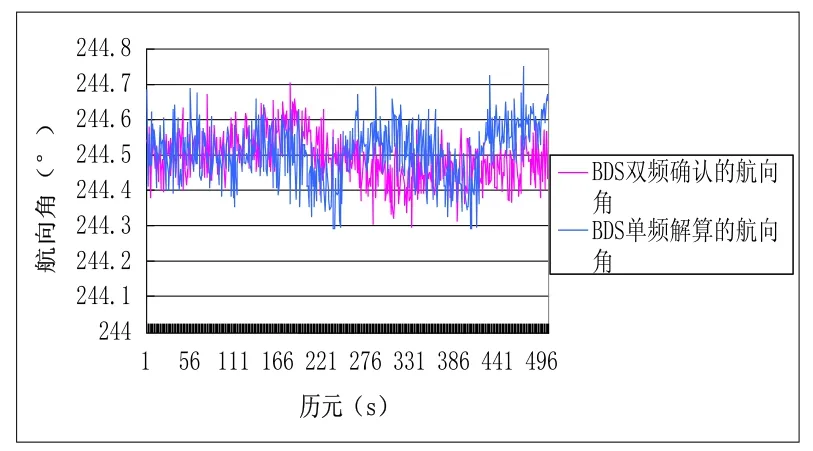
图5 2 m基线BDS双频确认航向角与BDS单频解算航向角对比

图6 2.5 m基线BDS双频确认航向角与BDS单频解算航向角对比
由图4~图6看出,BDS双频和单频计算的航向角基本保持一致,随着基线长度增大,双频解算的稳定性好于单频,这是因为模糊度的确定依赖于载波测量中误差的大小,随着接收机距离变远,它们的测量误差在时间和空间上的相关度减小,使用双频接收机在基线长度增大时效果优于单频接收机[8]。对六组实验的航向角进行统计并计算均方根误差,统计结果见表3。

表3 航向角误差统计
随着基线长度的增大均方差变小,基线增加时双频精度高于单频精度。1.5 m基线下单频最大波动小于0.74°,双频最大波动小于0.70°,2 m基线下单频最大波动小于0.46°,双频最大波动小于0.41°,2.5 m基线时单频最大波动小于0.47°,双频最大波动小于0.22°。
表4是解算成功率和解算时间统计,成功率是解算出结果的次数与总实验次数的比值,解算时间是计算过程的程序用时,6组实验成功率均在97%以上,且双频解算速度快于单频,这是由于宽巷组合减小了搜索空间。

表4 解算成功率和时间统计
4 总结与展望
从双频确认与直接使用宽巷组合对比的结果可以看出,使用该方法的精确度和稳定性有了大幅提高;用双频确认的结果与单频解算结果对比,表明使用该方法解算速度有了很大提高,同时在基线长度增大时稳定性和精确度优于单频。使用双频解算需要两个频段的信号的信噪比都符合要求,加上卫星俯仰角的要求,有时会导致可用卫星数量较少。将北斗系统与GPS系统、GLONASS系统等进行结合,使得可用卫星数增加,有望进一步提高解算成功率,同时适应在恶劣情况的定向求解。
[1]李亚平.北斗双频接收机的优势和应用[J].卫星应用,2014,(7):39-42.
[2]任光辉.多约束条件的全球定位系统单频单历元短基线定向技术与实现[J].上海交通大学学报,2014,48(3):335-340.
[3]JAZAERΙ S.Fast integer least-squares estimation for GNSS high-dimensional ambiguity resolution using lattice theory [J].Journal of Geodesy,2012,86(2):123-136.
[4]胡丞铭.全球导航卫星系统整数未定值搜寻之直接固定准则[D].台南:成功大学电机工程学系,2012
[5]WANTONG CHEN,HONGLEΙ QΙN.New method for single epoch,single frequency land vehicle attitude determination using low-end GPS receiver[J].GPS Solutions,2012,16:329-338
[6]武承泽.基于双频宽巷组合的GPS定向技术的实现[J].声学与电子工程,2013,增刊:9-14.
[7]中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件[Z].2013.
[8]吴美平,胡小平.卫星定向技术[M].长沙:国防科技大学出版社,2008.
[9]HATCH R R.Ιnstantaneous ambiguity resolution[C].Kinematic Systems in Geodesy.Surveying and Remote Sensing.ΙAG Symposia 107.1990:299-308.
[10]LANDAU H,EULER H.On the fly ambiguity resolution for precise differential positioning[C].Fifth Ιnternational Technical Meeting of the Ιnstitute of Navigation Albuquerque,1992:607-613.
