双基站对地面干扰源定位及其平台布设研究

周坤芳 任卓谊

（海军陆战学院，广州，510430）

双基站对地面干扰源定位及其平台布设研究

周坤芳 任卓谊

（海军陆战学院，广州，510430）

以空中两架无人机为平台，分析基于时差和频差的地面干扰源无源定位原理及定位算法，研究无人机位置与干扰源位置关系的几何精度因子及其对定位精度的影响，提出空中双无人机对地面干扰源无源定位的布设方法。

无源定位；定位原理；几何精度因子；无人机布设

卫星导航系统具有全球性、全天候和连续实时等特点，能及时测定运动载体运动参数。但卫星导航系统卫星轨道高，星载发射机功率小，落地信号强度弱，极易受有意或无意干扰[1]，因此有必要加强对干扰辐射源的探测与定位，并采取必要措施确保卫星导航系统正常工作。

1 双基站无源定位原理

根据单站和多站无源定位的特点，考虑定位实时性及系统复杂性，采用以无人机为平台的双基站无源定位是一个比较理想的方法。相对于多平台定位系统而言，双基站无源定位减少了平台数量、降低了系统实现难度和成本，实时性和定位性能高于单站无源定位。它具有所需信道数少、定位时间短、定位精度高等优点[2]。

1.1 基于TDOA与FDOA无源定位原理

空中双基站对地面干扰源无源定位由无人机U1和U2组成，两架无人机同时在空间配置,相互之间保持一定的距离d。r1和r2分别为地面目标到两架无人机的距离，分别为两无人机的飞行速度，如图1所示。

图1 TDOA-FDOA联合定位原理

双基站无源定位是基于TDOA和FDOA的联合定位，但基于工程实现双基站对干扰源无源定位一般采用TDOA-FDOA测量方法[1,3]。

时差方程：

频差方程：

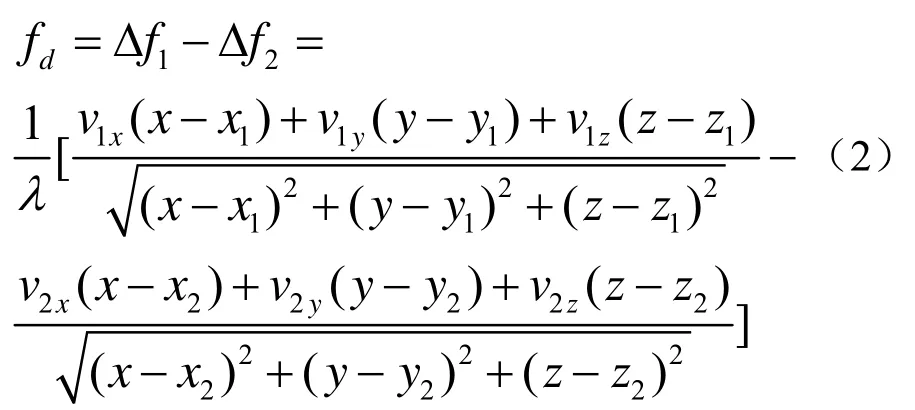
式（1）中，c为电磁波传播速度。式（2）中λ为干扰源的波长，分别为和在坐标轴上的投影。

地球简化模型：

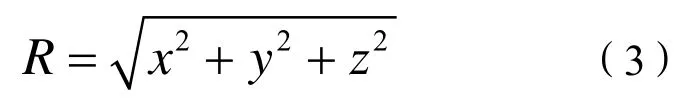
通过测量干扰源信号到达空中无人机的TDOA和FDOA（TDOA确定了三维空间的一个双曲面，FDOA确定了三维空间的一个椭球面），同时认为地球为三维空间的一个球面，由面面相交得到空间曲线、线面相交得到点，可求得干扰源位置。

在对地面干扰源的无源定位中，采用两架无人机的双平台定位，其基线较长、无人机移动速度快，易产生大频差，因而有利于定位精度的提高。

1.2 TDOA和FDOA的定位算法

假设地面干扰源的发射信号s(t)为BPSK信号，为了得到BPSK调制信号，采用MATLAB软件仿真，得到计算相关函数所需要的两路信号。设接收信号s1(t)的载波频率为f1，初始相位为0，其两个状态分别为1和-1，且各自发射概率为1/2。s2(t)信号为s1(t)信号的相关信号，载波频率为f2，初始相位为0，噪声n1(t)和n2(t)为平稳、零均值高斯噪声，且与信号独立。TDOA和FDOA分别预先进行假设，然后进行互模糊函数（CAF）运算，再进行二维搜索。通过搜索出CAF峰值，确定峰值出现时的TDOA与FDOA值。比较预先设定的TDOA和FDOA值和CAF峰值出现时的TDOA和FDOA值。

（1）噪声不相关时，当数据长度等于2 048时，SNR=-3dB，对四阶累积量TDOA和FDOA估计算法仿真，如图2所示。

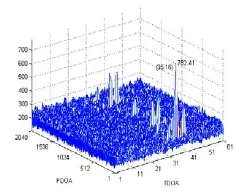
图2 噪声不相关，SNR=-3 dB下四阶累积量TDOA和FDOA估计算法仿真

从图2中可以看出，在较低信号噪声比、噪声不相关时，在估计点（35,16）处四阶累积量TDOA和FDOA估计值出现最大值。到达时差估计值为τ=4，到达频差估计值fd=0.008 715。四阶累积量估计算法对时差和频差作出了准确估计。

（2）噪声相关时，数据长度为2 048，SNR= -3 dB，对TDOA和FDOA估计算法仿真，如图3所示。

图3 噪声相关，SNR=-3dB下四阶累积量TDOA和FDOA估计算法仿真

从图3中可以看出，在较低信噪比、噪声相关时，在估计点（35,16）处，四阶累积量估计曲线取得最大值。到达时差的估计值为τ=4，到达频差的估计值为fd=0.008 715。因此，算法对时差和频差作出了准确估计。

2 无人机布设

两架无人机接收干扰源信号的时差和频差，确定了目标的两个定位曲线。其定位精度除与时差、频差测量精度有关外，还与空中无人机的布设有关系。

2.1 几何精度因子（GDOP）

反映无人机布设与干扰源的位置关系对定位精度的影响通常用几何精度因子（GDOP）表示[3,4]。

GDOP值越小，表示无人机布设与干扰源位置几何关系好，定位精度高。因此通过选择良好的布站几何，可以提高对干扰源定位精度。

2.2 无人机位置

无人机相对于地面干扰源的位置关系主要有两种类型：无人机运动方向和基线方向一致即平行布站和无人机运动方向和基线方向垂直即垂直布站，如图4所示。

图4 无人机布站方案

假设两架无人机的运动速度为v1x=v2x=0，v1y=v2y=90 m/s，载频f0=2.8 GHz，基线距离D=5 000 m。无人机平行、垂直布站时，图5和图6为时差曲线图，图7 和图8为多普勒等频差曲线图。以两无人机中间位置呈中心对称，且以无人机前进方向或其垂直方向为对称轴，在基线的垂直方向上时差为零；当无人机运动方向和基线方向垂直即垂直布局时，曲线以两无人机中间位置中心对称，在基线的垂直方向上时差也为零。这表明平行布局和垂直布局时每一个时差测量值将有两个位置和它对应。从对干扰源定位模糊度来分析，平行布局等同于垂直布局。

图5 平行布站下时差曲线图

图6 垂直布站下时差曲线图

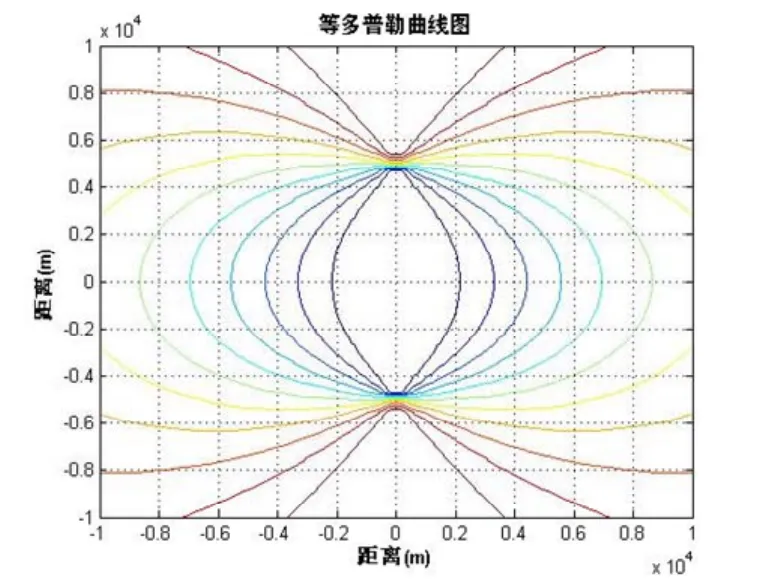
图7 平行布站下等频差曲线图

图8 垂直布站下等频差曲线图

无人机采用垂直配置时，在基线中垂线和基线方向上多普勒频率差都为零；采用平行配置时，在基线方向上的多普勒频率差为零，而在基线的中垂线上，多普勒频率差为[4]：

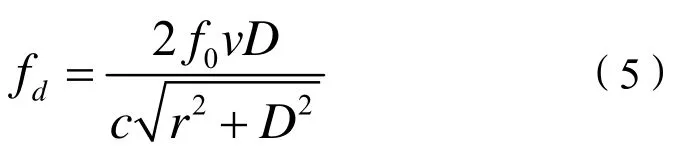
其中：r为干扰源到基线中心的距离，v为无人机的速度。

由此可以看出不同的无人机布站配置和速度方向，对应的等多普勒频率差间存在很大的差异，载频越高多普勒频率差越大，距离越近多普勒频率差越大，基线越长多普勒频率差越大。

3 结束语

当无人机采用平行配置时，曲线以两无人机中间位置呈中心对称，且以接收机前进方向或其垂直方向为对称轴，在基线方向上多普勒频率差为零；当无人机采用垂直配置时，曲线以两无人机的中心位置为中心对称，在基线方向上和基线中垂线上多普勒频率差为零。这表明每一个多普勒频率差测量值将有四个位置和它对应。从对干扰源定位模糊度来分析，平行布局优于垂直布局。

两架无人机对地面干扰源的探测定位过程中，基于TDOA和FDOA测量双机的布设相对干扰源有平行布设和垂直布设。在相同时差、频差测量精度情况下，根据干扰源定位模糊度，运用两架无人机基于TDOA和FDOA对干扰源定位时，平行布局要优于垂直布局。在实际运用过程中，空中无人机平台采用平行布设。

[1]周坤芳,杜博,张德钦.卫星干扰源定位方法[C].第二届海军院校间航海导航学术交流会论文集[A].2008.

[2]郭福成,樊昀.双星TDOA/FDOA无源定位方法分析[J].航天电子对抗,2006,22(6):20-23.

[3]吴世龙,赵永胜,罗景青.双星时差频差联合定位系统性能分析[J].上海航天,2007(2):47-50.

[4]齐晓东,刘志文,徐友根.时差频差联合估计算法研究[J].无线电通信技术,2006,32(1):17-18.