自动舵性能检测平台中船舶运动模型的建立
2015-01-09许星光刘勇臧涛贾玉柱
许星光刘勇臧涛贾玉柱
(1.海军工程大学导航工程系,武汉,430033;2.海军驻武汉701所军代室,武汉,430060)(3.武汉船舶职业技术学院,武汉,430050)
自动舵性能检测平台中船舶运动模型的建立
许星光1刘勇1臧涛2贾玉柱3
(1.海军工程大学导航工程系,武汉,430033;2.海军驻武汉701所军代室,武汉,430060)(3.武汉船舶职业技术学院,武汉,430050)
以国际电工委员会制定的“航迹控制系统性能及检测方法”为标准,基于MMG分离型建模思想,建立五自由度的船舶运动数学模型,搭建自动舵性能检测平台。实现在陆基条件下对自动舵的性能进行检测,并在测试过程中模拟船舶的运动。
自动舵;船舶运动数学模型;性能检测平台;分离型建模
自动操舵仪是现代船舶上不可缺少的导航设备,用于自动控制舵机,保持船舶按规定航向航行。搭建自动操舵仪性能检测平台的主要目的是实现在陆基条件下构建自动舵的模拟运行测试及性能检测环境。建立模拟运行环境,要求自动操舵仪与性能检测平台之间的各种输入、输出信号的电气特性要与实际相一致。本设计采用的是物理模拟与数字模拟相结合的方式来搭建自动操舵仪性能检测平台,由自动操舵仪、船舶运动数学模型以及舵角、航向模拟装置组成的闭环系统,符合国际电工委员会制定的航迹控制系统性能标准[1],并在其基础上进行了扩展。
检测自动舵的运行与性能的标准不同,性能检测要求船舶运动模型更为精确合理。现有运行平台采用的是线性化模型经简化后的野本方程[2],将操纵运动看作舵角的输出响应。而船舶运动本身是非线性的,因此,本设计参考MMG(Manoeuvring Mathematical Group)分离型建模的理论,建立了五自由度的船舶运动数学模型。
1 检测平台运行流程
性能检测平台对自动操舵仪进行性能检测的流程主要分为如下4步。
1)设定参数 船舶基本参数、船舶运动以及海浪干扰的相关参数是建立船舶数学模型的基础。选择典型船型作为不同吨位船舶的参考,也可以手动输入船体以及舵、螺旋桨的相关参数,以实现对各类船舶运动过程的精确模拟。船舶运动初始参数包括船速、初始舵角、初始航向、初始船位等。海浪的相关参数主要包括海浪周期和有义波高等参数。
2)设定航线 航线由各个航路点串联而成,船舶运动过程中以此作为基准,依次通过各个航路点,最后到达指定位置。
3)建立模型 将船舶基本参数、船舶运动初始参数以及海浪的相关参数送入性能检测平台中,建立船舶运动数学模型,利用龙阁-库塔法对相关参数进行计算,求解出船舶位置以及船舶线速度、纵摇和横摇角速度,将数据按照一定的格式发送给自动操舵仪。
4)数据分析 将实际航线(/航向)与设定航线(/航向)相比较,针对偏航量进行分析讨论,从而检测自动操舵仪的性能。

图1 自动操舵仪性能检测平台运行流程
2 船舶运动数学模型的建立
船舶运动模型可分为线性化模型和非线性化模型。线性数学模型是船舶操纵性的理论基础,但非线性模型不容忽视。船舶运动十分复杂,在平台中建立船舶运动数学模型需采用非线性化模型,只有这样,才能在更广阔的范围内更精确地反映原型的特性细节,发挥更好的效能。
船舶在水面运动时,存在六自由度的运动。在船舶运动和控制领域,人们首先关心的是航向角及航行轨迹的变化。对于大多数船舶来说,纵摇、横摇和垂荡影响较小,可忽略其对船舶水平面内的运动,即只考虑纵向、横向和艏摇三自由度的运动,但对于回转时横倾角比较大的船舶,如集装箱船、滚装船和高速军舰,横摇、纵摇运动使得船体所受流体动力发生显著变化,从而影响船舶在水平面内的运动,因此需要从五个自由度对船舶运动进行分析。
2.1 MMG模型简介
日本拖曳水池委员会(JTTC)为适应开发高性能船舶操纵模拟器的需要,于上世纪70年代末提出了MMG船舶运动模型。该模型的特点是将作用于船舶上的流体动力和力矩按照物理意义,分解为作用于裸船体、敞水螺旋桨和敞水舵上的流体动力和力矩,以及它们之间的相互干涉流体动力和力矩。
MMG模型建立在深层次的理论分析与广泛的试验研究相结合的基础之上,其优点是模型中的各项都具有明确的意义,便于进行设计上的局部修改,通过实验求得数学模型中的各项系数。
2.2 坐标系的选取
在分析船舶在海平面上的五自由度运动时,通常使用双坐标系统:即惯性坐标系与附体坐标系。Oξηζ为固定于地球表面的惯性坐标系,取作基准参考系统。O可取为海面或海中某一点,Oξ轴保持水平,一般以船舶的主航向为Oξ轴的正向,Oξ轴和Oη轴置于水平面内,Oζ轴垂直于坐标平面,其正向指向地心,该坐标系固定不动,用来描述波浪运动;Gxyz是原点位于船舶重心G上的附体坐标系,规定x轴指向船艏,y轴指向右舷,z轴指向龙骨,用来描述船舶运动。

图2 惯性坐标系和附体坐标系
惯性坐标系与附体坐标系有如下的转换关系:
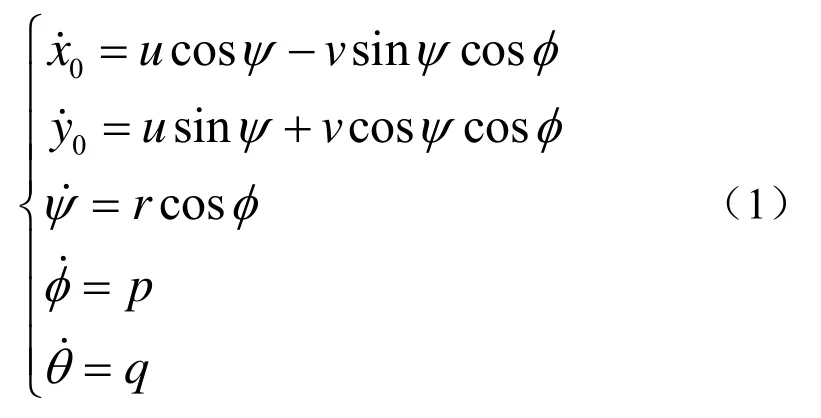
在惯性坐标系中,x0和y0为航行轨迹,ψ为航向角,φ和θ分别为船舶横倾角和纵倾角。在附体坐标系中,u和v分别为纵向和横向速度,r、p和q分别为艏摇、横摇和纵摇角速度。
2.3 运动方程
本文基于MMG分离型建模的基本思想,分析船舶在水中的运动规律,将作用于船体上的力和力矩分为船体、螺旋桨、舵和波浪干扰力和力矩[3]。船舶五自由度方程是一个非常复杂的方程组,涉及多个变量的求解,下式为性能检测平台中建立的船舶运动数学模型:

式中,m为船舶质量,mx和my分别为x和y方向上的附加质量,Ixx、Iyy和Izz分别为船舶对于x、y和z轴的转动惯量,Jxx、Jyy和Jzz分别为对x、y和z轴的附加惯性矩,下标H、P、R和WAVE分别表示船体、螺旋桨、舵和波浪。
本文主要研究的是包括纵向、横向、转艏、纵摇和横摇在内的五个自由度的运动。利用龙阁-库塔法求解上述微分方程的数值解,得到船舶运动位移和欧拉角以及相应的速度和角速度,提供给自动操舵仪性能检测平台中的其他模块。
本文以S175集装箱船作为研究对象,该船舶主尺度如表1所示。船体、螺旋桨以及舵的水动力采用多元回归公式或者估算公式进行计算。

表1 船舶主尺度表
以纵向流体动力的计算为例,对船舶所受的力和力矩进行计算。
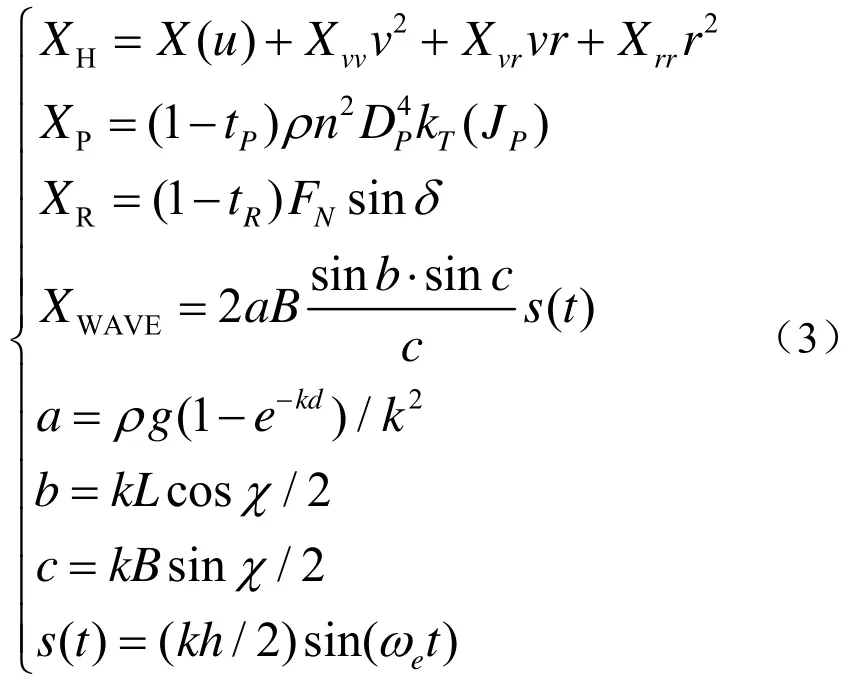
其中,X(u)为船舶直航阻力,在实际表达上,直接将X(u)拟合成u的多项式;Xvv为流体动力导数;tP为螺旋桨推力减额系数;JP为进速系数;n为螺旋桨转速;DP为螺旋桨直径;tR为舵力减额系数;FN为垂直于舵叶平面的舵的正压力;δ为舵角;X为遭遇角。
分别对初始舵角为5°、10°、15°、20°、25°、30°、35°的船舶回转运动进行数值模拟,图3为在静水中船舶在不同操舵下的轨迹图(从左舵35°到右舵35°)。航迹曲线形成了稳定的回转圈,且随着舵角的增大,回转圈直径越来越小,符合操纵规律。

图3 不同舵角下的回转运动仿真
Z型操纵试验的目的是评价船在中、小舵角下改变和保持航向的能力,图4给出了船舶初速度为16 kn时,±15°舵角下的Z型操纵仿真结果,仿真结果与相似船舶试验结果符合较好。

图4 ±15°舵角下Z型操纵仿真
3 海浪建模与仿真
3.1 ITTC双参数谱
船舶在海中航行时,总会受到来自海浪的干扰。对于无限水深的海面,第15届ΙTTC会议推荐使用修正的Pierson-Moskowits波谱(MPM谱)来描述海浪运动。其谱密度为

该谱为双参数谱(ζ1/3,T1),ζ1/3为有义波高,T1是平均海浪周期,ω为海浪角频率。在ζ1/3=4 m,T1=7 s的条件下,ΙTTC双参数海浪谱如图5所示。

图5 ΙTTC双参数谱
3.2 建模与仿真
国际上按波浪等级划分海况,根据不同的有义波高,一般分为0~9级。对随机海浪仿真的思想是,先将随机海浪在仿真阶段进行离散化,根据离散的海浪谱确定在各个特定频率下的谐波波倾角,再确定各谐波的初相角,然后将各个谐波的波倾角叠加起来就得到仿真的长峰波随机海浪波倾角。根据上述仿真思想,空间某一固定点的海浪波倾角的仿真模型为:
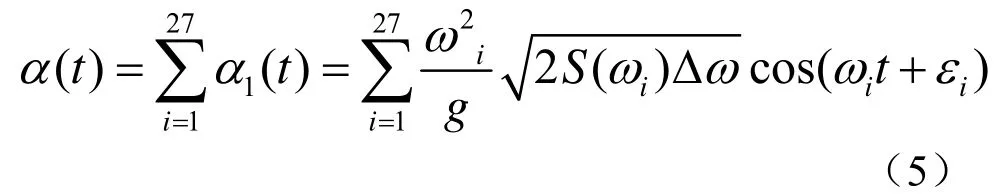
各个谐波的初相角(iε)为在0~2π间均匀分布的随机相位,在系统仿真时可以通过一个在(0,1)均匀分布的伪随机数来产生。图6为五级海浪(ζ1/3=4 m)的波面图。

图6 五级海浪下波高仿真图
3.3 海浪作用下的船舶运动
船舶在回转过程中所受的波浪力主要为波浪干扰力和波浪漂移力。在附体坐标系上,除横向波浪力外的其他各波浪力都是以波浪主干扰力为主,横向波浪力以波浪漂移力为主。在船舶航行过程中,波浪的二阶漂移力会对船舶航行的航向和航行轨迹产生影响。图7和图8分别是在29 kn航速,左舵35°,迎浪和横浪条件下船舶的回转轨迹仿真结果。

图7 迎浪条件下回转轨迹

图8 横浪条件下回转轨迹
从图中可以看出,船舶航行轨迹会沿着波浪方向移动。回转圈向波浪前进方向拉伸,形成类似椭圆形的轨迹曲线。
4 结语
利用船舶运动数学模型,根据计算机仿真进行船舶操纵性能的预报是较为有效的,也是最经济的一种方法[4]。本文基于MMG分离型思想,通过分析船体、螺旋桨、舵以及海浪产生的力和力矩,建立船舶运动数学模型。对于各种流体动力导数和干扰系数的确定,从实用的角度出发,将理论计算结果与约束船模试验结果、数据库中的数据相结合而总结出的近似估算公式来确定船体流体动力的导数。研究证明,这种方法的计算精度已达到工程要求。
应用该数学模型,可以模拟船舶在不同操舵模式下的运动。通过与文献[3]中的实验对比,回转运动以及Z型操纵运动仿真结果与实验结果较为相似,说明模型正确合理,可以应用于自动舵性能检测平台中。
[1]ΙEC.Track control systems - Operational and performance requirements,methods of testing and required test results:ΙEC 62065-2002 [S].2002.
[2]陈永冰,周岗,李文魁.舰船航迹控制系统运行检测平台的设计与实现[J].海军工程大学学报,2011,23:38-42.
[3]HΙRANO M,TAKASHΙNA J,TAKAΙSHΙ Y,et al.Ship turning trajectory in regular waves[J].West Japan Society of Naval Architects,1980,60:17.
[4]KAWABE HΙROSHΙ,OZAKΙ,HAKUYA.2007s-G6-2 Estimation of sailing condition of ryukyuan tribute ship[C].The Japan Society of Naval Architects and Ocean Engineers,2007:125-128.
