基于嵌入式linux的无人机双目视觉系统

李源哲 茅旭初

（上海交通大学电子信息与电气工程学院，上海，200240）

基于嵌入式linux的无人机双目视觉系统

李源哲 茅旭初

（上海交通大学电子信息与电气工程学院，上海，200240）

无人机技术持续发展，立体视觉技术由于其强大的环境感知能力，被广泛应用于无人机导航的障碍物检测中。针对无人机障碍检测的特定场合，设计了基于嵌入式Linux的双目视觉测距系统，系统具有体积小、重量轻、精度较高的特点，可用于无人机障碍物检测。

双目立体视觉；嵌入式；无人机

1 引言

近年来，无人机在民用领域逐渐发展开来。导航技术是无人机技术中相当关键的部分，也是无人机技术的难点[1]。大型无人机的飞行高度较高，很少受到周围物体的阻碍，一般使用GPS+ΙMU的组合导航来完成。对于多旋翼无人机，尤其在城市、山地等复杂地形中低空工作的多旋翼无人机，由于建筑、地形的阻挡，GPS信号较弱，搜不到足够的卫星数目，导致导航精度不理想。并且，对于在低空甚至室内飞行的飞行器，仅仅知道位置信息往往不够，飞行器随时会遇到墙壁、树木等低空障碍物，这时，就需要能够感知外部环境的导航系统。目前主要的导航方式分为两大类：

（1）基于非视觉传感器的导航

非视觉传感器，主要是超声波、激光等能够探测障碍物距离的传感器。超声波传感器是通过计算超声波发射和接收的时间差来计算障碍物的距离，因其简单、轻便，在多款飞行器上使用。但超声波的探测角较小，只有某一特定方向的障碍物才会被检测出来；且超声波对被测物体的要求较高，若物体无法有效反射超声波，如树叶、海绵等，则无法被探测到。因此超声波传感器无法全面感知周围的环境。 激光雷达，通过向不同方向发射激光束来探测物体距离，具有精度高、视场宽、分辨率高的特点。但是激光雷达成本高、重量大，不适合载荷较小的飞行器。

（2）基于视觉传感器的导航

视觉传感器，一般指摄像头，具有质量轻、成本低、信息量大的特点，十分适合用在小型无人机的导航。随着图像处理技术的蓬勃发展，对图像处理、目标识别、特征提取、3D视觉等技术的研究愈加深入，视觉导航的技术也将更加成熟。在单目视觉中，主要通过光流法来检测障碍物，这种方式依赖于摄像机与目标的相对运动，若飞行器处在静止或者低速状态，则效果不明显。多目视觉能够直接计算出空间中特征点的三维坐标，与光流法相比，对飞行器运动的依赖较小，结果更加精确。

通过上述比较可以看出，立体视觉技术能够很好地感知位置场景，帮助无人飞行器进行低空的障碍物检测，辅助飞行器进行运动控制，拥有巨大的应用前景。

本文提出了一种在嵌入式linux系统上实现双目视觉检测的方法。系统基于ARM cortex-A9 架构的单板电脑，读取两个USB摄像头的信息，经过3D解算得到周围环境特征点的3维坐标，可用于无人机导航。

2 双目立体视觉原理

2.1 摄像机成像模型

图1是摄像机的针孔成像模型。针孔成像模型由光心、光轴和成像平面组成。光心为一凸透镜，物点P的反射光经过光心后，投射到成像平面为一个倒立的像p。其中f是相机的焦距，Z是相机和实际物体之间的距离，X是实际物体的长度，x是实际物体在成像平面上的像[2]。在图1中，根据相似三角形原理，可以得到：

图1 摄像机针孔成像模型

2.2 成像模型中各坐标系之间的关系

摄像机成像模型中包含四个坐标系：世界坐标系、摄像机坐标系、图像物理坐标系和像素坐标系。物点（实际空间中的点）到像点（投影到成像器件上的点）之间的关系可以通过坐标变换来表示。

2.2.1 从世界坐标系到摄像机坐标系的坐标变换

摄像机被放置在三维空间中，在这个三维环境中建立的坐标系是世界坐标系，如图2中的(Ow-XwYwZw）。以摄像机的光心O为原点，光轴为Zc轴，建立的坐标系为摄像机坐标系，如图2中的(O-XcYcZc)。

图2 成像模型中的各个坐标系

摄像机坐标系与世界坐标系的关系可利用旋转矩阵R和一个平移矩阵t表示，变换过程如下：

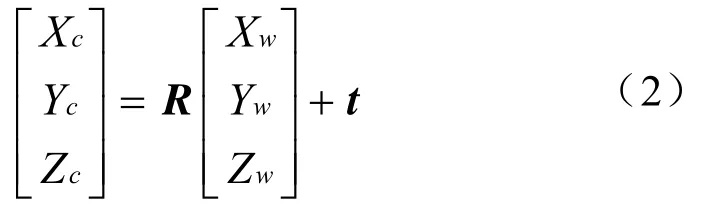
其齐次坐标可表示为：

2.2.2 从摄像机坐标系到图像物理坐标系的坐标变换

图像物理坐标系是建立在成像平面上的直角坐标系。原点O1是光轴与成像平面的交点，x轴与Xc平行，y轴与Yc平行。根据三角形相似的性质，摄像机坐标系到图像物理坐标系的变换如下：

用齐次坐标与矩阵形式可以将上式表示为：

2.2.3 从图像物理坐标系到图像像素坐标系的坐标变换

拍摄到的照片以矩阵的形式保存，每个矩阵元素都是一个像素。与之对应，图像像素坐标系是定义在图像上的平面直角坐标系，其单位是像素。图2中，O0-uv是图像像素坐标系。原点O0位于图像的左上角，u和v分别与x轴和y轴平行，坐标(u,v)表示位于第u行v列的像素点。

由于图像物理坐标系的原点O1和图像像素坐标系的原点O0未必重合，假设O1在图像像素坐标系中的坐标为(u0,v0)。设每个像素在图像物理坐标系x轴和y轴方向上的物理尺寸分别为k和l，则：

用齐次坐标与矩阵形式可以将上式表示为：

综合上述坐标变换，可以将世界坐标系中的物点P（Xw,Yw,Zw）变换到成像平面上的投影点Pu（u,v）：

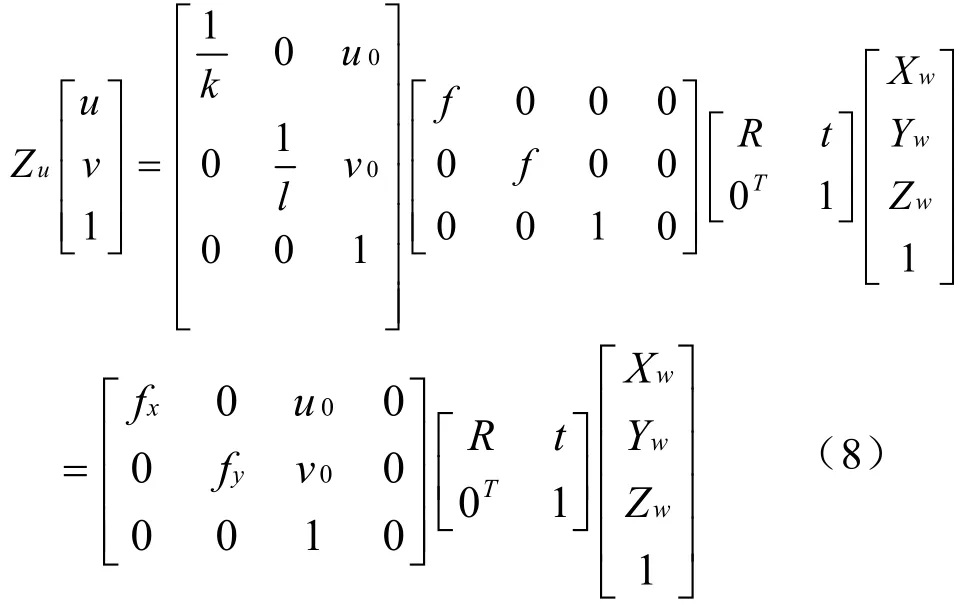
2.3 立体视觉成像模型

双目立体视觉成像模型如图3所示，两个摄像头并排放置。Ol和Or分别是左右摄像机的光心，两个光心间的距离为T，P为真实空间中的一点，它在左右两个摄像机的成像平面上的成像分别是pl(xl,yl)和pr(xr,yr)。在这个简化的模型中，深度与两张图的不一致性成反比，其中，不一致性定义为d=xl-xr。根据相似三角形原理，深度为：

图3 双目视觉成像模型

2.4 立体视觉工作流程

立体视觉系统的工作主要分为五个步骤：图像获取、摄像机建模、特征提取、立体匹配和三维深度确定[1]。

（1）图像获取

采集两个并排放置的USB摄像头的图像。

（2）摄像机建模

摄像机建模的工作是为了确定摄像机的内外参数，将复杂的模型转换为简单的基础模型，并确定空间中的点与像素点的对应关系。摄像机标定可以确定摄像机的参数。

（3）特征提取

图像特征是把图像中的像素点或者像素点的集合抽象表达的过程。图像中包含大量的信息，特征提取的作用就是从大量信息中提取出感兴趣的部分，以便后续的分析。

（4）立体匹配

立体匹配是在两张图像的特征点中，找到分别对应相同实际物体的两个特征点，即找到了实际物体在两张图片中的像素值。

（5）三维坐标确定

立体匹配确定实际空间中的点在两张图片中的图像坐标，根据多重视觉几何算法，可以解算出空间点的三维坐标。

3 摄像机标定

摄像机标定包括单目摄像机标定和立体摄像机标定。单目摄像机标定是为了确定摄像机模型中各个坐标系之间的关系，从而确定摄像机的内外参数[1]。立体摄像机标定是为了确定两个摄像机坐标系之间的刚体变换关系，即一个摄像机坐标系相对于另一个摄像机坐标系的旋转和平移[3]。

3.1 内外部参数

引入两个不同的焦距fx和fy。fx=f/k,是焦距与像素点宽度的比值，fy=f/l，是焦距与像素点长度的比值，fx和fy的单位是像素。fx、fy、u0、v0构成摄像头的内部参数。两摄像头之间的旋转矩阵R和平移向量T构成了摄像机的外部参数。除上述参数外，由于工艺的原因，摄像机透镜可能存在畸变。因此，需要进行标定消除畸变。

对于某些透镜，光线在远离透镜中心的地方比靠近中心的地方更加弯曲，这种畸变称为径向畸变。径向畸变在成像中心处畸变为0，越靠近边缘畸变越显著。可以用r=0周围的泰勒级数展开来定量描述径向畸变：

式中，(x,y)是畸变点在图像中的原始坐标，（xcorrected,ycorrected）是校正后的新坐标，k1、k2、k3是校正参数。

另一种畸变是切向畸变。切向畸变是由于透镜与成像芯片不平行造成的。切向畸变可描述为：

其中，p1、p2是校正参数。

3.2 标定过程与结果

本文使用标定板进行标定，标定板长30 cm，宽20 cm，由直径16 mm、等距离间隔4 cm的6×5圆点组成。从不同距离、不同角度拍摄标定板，得到图4所示的标定照片，一般左右两个摄像头各拍摄十几张照片。标定后的各参数(以右摄像头为例)见表1。

图4 标定照片

表1 标定后的参数值

4 特征识别与匹配

4.1 SURF特征匹配

本文使用SURF(Speeded Up Robust Features)算法提取特征点。SURF算法能够检测图片中的角点，对于每个角点，SURF得到一个特征向量，该向量描绘了特征点周围的强度样式。两个特征点越相似，它们的特征向量也越靠近[4-5]。若两幅图像中的某特征点特征向量靠近，则有理由认为它们对应空间中的同一点。

数学上，SURF算法对每个像素计算Hessian矩阵，Hessian矩阵如下：

Hessian矩阵的行列式即曲率的强度，定义角点为具有较高局部曲率的图像点。为了使特征点具备尺度无关性，在进行Hessian矩阵构造前，对图片高斯滤波：

其中，σ是滤波器的高斯函数的方差，它定义滤波核的大小。

通过高斯滤波和Hessian矩阵，可以得到局部极大值，经过插值，得到亚像素精度的特征点以及对应的尺度值[6]。

编写程序，对两张照片进行SURF特征点匹配。结果如图5所示，其中，圆圈标记识别出的特征点，直线连接两图相匹配的特征点。

图5 SURF匹配效果

4.2 RANSAC算法去除错误匹配

从图5可见，大部分特征点都匹配正确，仍有少数点错误匹配。本文借助Ransac算法降低错误匹配的概率。

Ransac（随机抽样一致）算法可以从一组包含“局外点”的观测数据集中，通过迭代方式估计数学模型的参数。本文通过简单的例子解释Ransac，在图6中，白色点为局外点。为了找到点集的拟合直线，每次选取两个点，确定一条直线。定义一个距离阈值（在图中由虚线标出），落在虚线间的点构成一个一致集。每次选取不同的两个点，并确定它们的一致集，认为一致集最大的直线为拟合直线。在一致集外的点则被当做误差剔除。

图6 Ransac算法的简单应用

在立体视觉成像模型中，pl和pr之间存在如下关系：

该方程体现了两个对应点之间的联系，被称作极性约束。8个对应点可以确定F矩阵。因此，在所有特征点中，每次选取8对特征点，由此确定F。给定距离阈值△，选取满足以下关系的匹配点进入一致集：

一致集中匹配点最多的F即为选定的F，一致集中的匹配点则为所有选定的匹配点。匹配结果如图7所示。

图7 Ransac去除错误匹配后的效果

5 三维坐标计算

本文使用线性三角方法计算三维坐标。由射影几何的性质，空间中的点X与左右两个摄像头的像素点x、x′具有以下关系：

其中，P和P′分别为左右两个摄像头的投影矩阵，该矩阵可以通过标定得到。由式(18)可以得到方程：

将其展开：

其中，piT是P矩阵的第i行。令：

解线性方程AX=0，即得到三维坐标X。

6 硬件系统

本文使用radxa rock卡片电脑作为处理核心。radxa rock长10 cm，宽8 cm，搭载四核ARM Cortex-A9处理器，2G RAM，最高主频可达1.6 GHz，在节能状态下主频可低到324 MHz。板上安装ubuntu操作系统作为编程环境。用USB摄像头作为图像采集设备，系统借助V4L2采集摄像头的视频流（是V4L的升级版本），V4L全称是Video for Linux，是在linux内核中关于视频设备的APΙ接口，涉及开关视频设备、采集并处理视频图像信息。通过调用V4L2 APΙ中的函数，可以实现视频的采集。视频采集主要分为4个步骤： 打开视频设备，设置视频设备属性及采集方式，视频数据处理，关闭视频设备。流程如图8所示。系统通过V4L2采集左右两个摄像头的图像、提取特征点并对特征点进行匹配。最后，综合标定的参数，计算得到特征点的三维坐标。

图8 V4L2图像采集流程

7 实验结果及分析

为了测试系统的精度，制作了一个测量板，上面刻有10 cm长的标尺。系统分别计算标尺两个端点的三维坐标，求取它们的距离，得到标尺长度的测量值，并与真实值比较。本文中分别将标尺放在与摄像头相距50 cm、60 cm……150 cm的位置，测量结果在表2中列出。

表2 系统精度测量信息

对系统精度的测试中，在0.5～1.5 m的距离上，测量10 cm的标尺，误差在5 mm左右，相对误差在5%左右，其中，这5%的误差大部分是系统误差，经过更加仔细的定标之后，可以将误差降低至2%左右。

双目立体视觉系统体积小、质量轻，经地面测试，精度满足需求，可以用于无人机导航。接下来的工作将进一步把系统安装到无人机上，辅助无人机导航。

[1]罗桂娥.双目立体视觉深度感知与三维重建若干问题研究[D].中南大学,2012.

[2]BRADSKΙ G,KAEHLER A.Learning openCV:computer vision with the openCV library[M].O'Reilly Media,Ιnc.,2008.

[3]王建华,冯帆,梁伟,等.双目立体视觉测量系统的设计与实现[J].舰船电子工程,2012,32(4):107-109.

[4]Laganière R.openCV 2 computer vision application programming cookbook:over 50 recipes to master this library of programming functions for real-time computer vision[M].Packt Publishing Ltd,2011.

[5]HARTLEY R,ZΙSSERMAN A.Multiple view geometry in computer vision[M].Cambridge university press,2003.

[6]王平,韩燮,韩焱,等.基于双目视觉技术的物体深度信息的提取[J].科学技术与工程,2014 (2):56-61.