基于“空间双拐点”估计的环境库兹涅茨曲线

刘舜佳

(湖南农业大学 商学院，湖南 长沙 410128)

【统计应用研究】

基于“空间双拐点”估计的环境库兹涅茨曲线

刘舜佳

(湖南农业大学 商学院，湖南 长沙 410128)

基于污染空间扩散这一遗漏掉的非观测变量将传统线性环境库兹涅茨曲线在空间维度扩展成能同时测度环境污染与不同地区经济增长之间关系的“空间双拐点”模型。基于中国31个省区1990—2012年工业废气面板数据的检验结果显示：某一地区工业废气污染与辖域内、外不同地区经济增长之间的关系均呈倒U型，这一结论即使在置换包含不同邻域数的空间权重矩阵之后也具有稳健性，因此遏制工业废气污染需同时逾越辖域内、外经济发展“拐点”。随着产生污染空间扩散的毗邻地区数增加，改善工业废气污染所要求的辖域内经济发展水平趋于严格，辖域内“拐点”到来呈滞后趋势；而改善工业废气污染所要求的辖域外其他地区经济发展水平则随着地理毗邻关系减弱而趋于宽松。政策提示污染治理需国家层面整体推进、缩小区域间经济发展水平差距以及杜绝落后产业的区域间转移。

空间拐点；环境库兹涅茨曲线；空间扩散

一、问题提出

近期随着纪录片《穹顶之下》的播出，关于大气污染与经济增长之间的争议再一次引起普通民众的强烈关注。而学界对此研究可追溯到较早提出的环境库兹涅茨曲线(EKC)，Grossman和Krueger认为人均收入与环境污染之间存在倒U形曲线关系：经济发展初期，随着收入上升，环境污染指标上升；但当人均收入水平达到一定门槛后(经济“拐点”)①“拐点”的数学定义是指凸曲线与凹曲线的连接点，即该点的二阶导数为零。很明显，环境库兹涅茨倒U形曲线的“极大值”点在数学上只能称为“驻点”，即该点一阶导数为零；但学界亦有不少文献将该“驻点”称之为“经济拐点”(王立平等，2010)，本文沿用这一称法。，环境污染指标则开始趋于下降，环境质量逐步改善[1]3 914。之后基于不同国家的实证研究也大都证实经济发展与环境污染之间所存在的这种密切关系。

但对环境库兹涅茨曲线的批评之声也不绝于耳，其中一点直指其忽略了环境污染的空间相关性。之后针对该曲线的经验研究大都基于空间数据自相关特征或是污染排放的空间相关性来构建空间计量模型[3-4]。如Rupasingha等以Anselin提出的空间计量方法对美国3 029个县的人均收入与大气污染之间的关联进行了检验，结果显示空间变量的引入大大提升了模型估计的准确性[5-6]。之后，Maddison基于欧洲国家样本的分析也显示污染存在着显著的国家间溢出效应[7]。考虑到环境污染的空间相关性，Poon、Hosseini等的空间计量检验分别发现大气污染在中国省域之间以及亚洲各国之间存在着显著的空间溢出效应[4][8]。Hossein和Kaneko基于六种空间权重矩阵的研究也证实国家间存在着污染的空间溢出[9]。国内学者的研究大都也证实了污染在省域间的空间关联性，如张可和汪东芳、马丽梅和张晓、沈能等[10-12]。

上述经验研究已证实环境污染的空间相关性，因此环境库兹涅茨曲线对环境污染与经济增长之间关系的刻画可能也需要分区域来考查。一方面，某一区域经济发展直接降低了辖域内环境质量；另一方面，辖域外毗邻地区经济发展过程中所排放的污染物经空间扩散也会恶化辖域内环境质量。综合这两方面，某一区域环境质量就同时与辖域内、外经济发展水平密切相关，要遏制环境污染就必须同时逾越辖域内、外经济发展的“空间双拐点”。尤其是当辖域内济发展“拐点”与辖域外毗邻地区经济发展“拐点”并不重合甚至是在辖域外经济发展“拐点”滞后于辖域内经济发展“拐点”的情况下，单纯针对所在行政区划的环境污染治理措施可能是无效的。由此可见，环境污染与经济增长之间的关系本质上应是一空间交互过程(Spatial Interaction Process)。有必要对环境污染与经济增长之间的关系进行空间剖分。

二、“空间双拐点”的环境库兹涅茨曲线

采用空间计量模型实证环境库兹涅茨曲线形状或是扩展研究污染影响因素，已经成为当下重要分析工具，本文亦遵循这一主流研究范式。但本文创新在于：基于前文分析所得的“空间双拐点”假定，通过对传统线性环境库兹涅茨曲线嵌入代表区域相关性的污染空间扩散这一非观测变量，从而将其在空间维度扩展成为具有Durbin结构的空间计量模型；并结合实证样本的数据生成方式(Data Generate Process)，就其模型设定形式是否有别于污染文献当中常用的两种空间模型进行稳健性检验，从而论证本文在“空间双拐点”假定下进行模型推导的合理性；最后基于空间计量模型非线性结构的参数释义，给出“空间双拐点”定义。

(一)“空间双拐点”环境库兹涅茨曲线的建立

依据前文对“空间双拐点”假定的分析，某一区域环境污染(P)有两个空间来源：一是辖域内经济增长所排放的污染物，按照经典线性环境库兹涅茨曲线的解释，这一部分污染直接与辖域内经济增长相关，可用辖域内人均GDP(Y)及其二次项形式(Y2)加以表达。二是辖域外其他地区经济增长所排放的污染物经由空间扩散给辖域内所带来的污染增量，这一部分污染物虽来自辖域外其他地区经济增长过程中的排放，但经空间扩散后抵达到辖域内的污染增量并不完全取决于污染源地区的经济增长水平，而是在很大程度上受制于空间扩散的地理距离，本质上是一非观测变量(Z)，而经典环境库兹涅茨曲线恰恰未能对来自不同地区的污染物加以区分，导致这一非观测变量的遗漏。现予以补足后重写环境库兹涅茨曲线：

P=α+β1·Y+β2·Y2+θ·Z

(1)

其中α为截距项，β1和β2分别代表辖域内人均GDP及其二次项对环境污染的影响系数，θ则代表辖域外空间扩散而来的污染对辖域内环境质量产生的影响。如果这一具有非观测性的域外污染增量不与辖域内经济增长具有相关性，那么经典线性环境库兹涅茨曲线的估计也就不会带来任何估计偏误。然而，由于专业化分工所带来的区域间经济增长的正相关性，同时污染又是经济增长过程中的必然产物，因此某一地区经济增长与来自辖域外的污染增量之间势必存在着不可分割的关联，同时域外污染空间扩散增量的侵入也会对辖域内经济发展产生阻滞效应，因此，两者之间应互为因果关系[13-15]。对污染空间扩散增量这一非观测因素的遗漏势必会导致模型内生性偏误。考虑到污染空间扩散属性，参照Parent和LeSage处理空间遗漏变量的作法，用下列空间向量自回归式(Spatial Autoregressive Process)来对这一非观测因素进行描述[16]：

Z=ρ×W×Z+ε

(2)

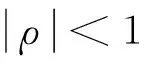
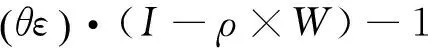
(3)

另外，一方面有大量文献指出一国经济增长绩效与其良好的制度因素密不可分，尤其是中国自20世纪80年代以来实施的改革开放政策对中国经济的快速发展提供了制度保障[17]；另一方面也有不少文献指出污染排放与制度安排紧密相关[18]。因此，再一次对式(3)中模型内生性问题进行审视，不能否认隐没于随机扰动项部分(θε)的另一非观测因素——制度变量，与模型当中经济增长变量之间所存在的关联，对于这一潜在相关性所可能导致的模型内生性问题，通常以经典计量回归关系式来予以控制：

θε=λ1·Y+λ2·Y2+v

(4)

其中参数λ1和λ2分别代表随机扰动项当中的非观测变量(制度因素)与模型当中观测变量(人均GDP)之间的相关性，v是在模型随机扰动项当中控制了这种相关性之后的剩余成份，通常可按经典计量作法假定其服从独立正态分布。在将式(4)代入到式(3)后，通过移项合并最终有：

P=C′+ρW·P+ξ1·Y+ξ2·Y2+ζ1W·Y+ ζ2W·Y2+v

(5)

其中C′=α(I-ρ×W)，ξ1=λ1+β1，ξ2=λ2+β2，ζ1=-β1ρ，ζ2=-β2ρ。式(5)与线性模型式(1)的区别在于其包含每一个自变量的空间滞后项，该空间滞后项衡量的是经空间加权平均后的辖域外经济增长对辖域内环境污染的影响，其结构形式与空间Durbin模型(spatial Durbin model，SDM)相同，即用于实证检验的“空间双拐点”环境库兹涅茨曲线。

(二)“空间双拐点”环境库兹涅茨曲线的稳健性

之前对环境库兹涅茨曲线的空间建模文献大都采用的是空间滞后模型(SLM)和空间误差模型(SEM)，因此，本文推导得到的“空间双拐点”环境库兹涅茨曲线在模型设定形式上是否与这两种常用的空间模型存在着显著性差异，这就需要进行检验。借鉴Ehlorst提出的空间模型设定形式检验方案，在一个更大范围的模型族中，就“空间双拐点”环境库兹涅茨曲线在设定形式上是否有别于常用的两种空间模型以及经典线性环境库兹涅茨曲线进行选择性检验[19]。该检验方案基于表1的面板数据模型为备选集给出如下检验步骤。

表1 面板数据模型备选集表

注：μi、λt分别代表截面、时期特异效应；wij为空间权重矩阵元素；i(j)和t分别代表截面和时期。

首先，就空间面板模型是否有别于传统线性面板模型进行选择性检验。以包含(或不包含)截面单元固定效应在内的传统线性面板模型的估计残差为基础，进行空间滞后项(SLM)与空间误差自相关项(SEM)的(稳健)LM检验。若检验结果显示线性面板模型遗漏掉空间滞后项(SLM)与空间误差自相关项(SEM)，则应否决线性面板模型是对样本数据生成方式的最适拟合，进入下一阶段来检验空间面板模型设定形式。

其次，由于空间Durbin模型在设定形式上嵌套(Nested)空间滞后模型与空间误差模型，因此，就设定形式最具一般性(General)的SDM是否在设定形式上有别于设定形式具有特异性(Specific)的SLM和SEM可进行约束性检验。原假设Ho如下：

SDM与SLM设定形式并无本质性区别，Ho：ζ1φ1=0，ζ2=0

SDM与SEM设定形式并无本质性区别，Ho：ζ1+ρ·ξ1=0，ζ2+ρ·ξ2=0

(6)

检验统计量为LR检验与Wald检验。根据所得到的空间模型参数约束性检验结果，空间面板模型甄选原则如下：如果以上两个原假设全部被拒绝，则SDM是对数据样本的最适拟合；如果以上两个原假设均无法拒绝，则对数据样本的最适拟合应在SLM和SEM这两种设定形式更为简洁的模型之间选择，选择标准可依据模型估计后所得到的对数似然值，取最大值一个；如果不能拒绝第一个原假设，且第一步检验结果也无法拒绝SLM，则SLM是对数据样本的最适拟合，同理适用于SEM；如果第一步检验结果与第二步检验结果互有冲突，例如，有可能出现第一步检验无法拒绝SLM，而第二步检验又无法拒绝SEM，则应该选用设定形式更为一般化的SDM，以此避免模型设定特异化所带来的估计偏误。

最后，就空间模型当中的截面单元是采用固定效应还是随机效应进行Hausman检验。

(三)“空间双拐点”定义

经典环境库兹涅茨曲线认为经济发展越过某一“拐点”后，环境污染便开始趋于下降，对这一经济“拐点”的计算是用人均GDP(Y)及其二次项(Y2)的参数估计值(分别大于0和小于0)来构造。照此逻辑，对于本文估计得到的“空间双拐点”库兹涅茨曲线，辖域内经济“拐点”可用人均GDP及其二次项的模型参数估计值来构造，辖域外经济“拐点”可用人均GDP滞后项(WY)及其二次项(WY2)的模型参数估计值来构造。但LeSage和Pace指出，由于空间模型放宽了原线性模型区域观测值彼此不相关的严格假定，使得样本数据当中某一地区自变量观测值不仅可以影响到所在地区因变量观测值，而且还可以通过空间关联影响到其他地区因变量观测值。因此，不能将空间模型中自变量参数估计值当作辖域内经济增长对污染的影响，也不能将空间模型中自变量空间滞后项的参数估计值当作辖域外经济增长对污染的影响。LeSage和Pace建议采用偏导矩阵法重新界定自变量从辖域内、外两个空间区域对因变量所施加的影响[20]33-70。以式(5)为例，重组方程：

P=α+(I-ρW)-1[ξ1·Y+ζ1W·Y]+ (I-ρW)-1[ξ2·Y2+ζ2W·Y2]+ (I-ρW)-1v

(7)

以自变量Y为例，不同截面单元(i=1,…,N)因变量对不同截面单元自变量的偏导矩阵如下：

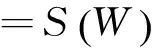
(8)

自变量Y对因变量P的影响是用式(8)中矩阵对角元素之和的平均值来衡量：*tr(·)代表对偏导矩阵对角元素的加总求和。t是元素值全为1的横向量，t=[1 … 1]1×N。

(9)

自变量空间滞后项WY对因变量P的影响是用式(8)中矩阵非对角线元素行和平均值来衡量：

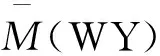
(10)

分别基于式(9)和式(10)定义的自变量及其空间滞后项对因变量的作用力与式(5)当中自变量参数估计值ξ1(线性模型下将其当作自变量Y对因变量P的影响力)及其空间滞后项参数估计值ζ1(线性模型下将其当作自变量空间滞后项WY对因变量P的影响力)在数值大小及符号方向上可能存在根本区别，这得到了Elhorst、LeSage和Pace实证结果的支持[19][20]33-70。*Elhorst(2012)和LeSage和Pace(2009)分别基于面板与截面数据的经验结果证实基于偏导矩阵定义的自变量对因变量影响的估计值与SDM参数估计值的数值符号是完全相反的[19-20]。

在得到空间模型当中自变量及其空间滞后项对因变量影响的准确测度后，按环境库兹涅茨曲线对经济增长与环境污染之间关系的描述，“空间双拐点”界定如下：

(1)辖域内经济增长“拐点”

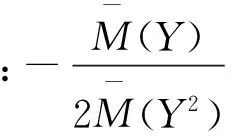
(2)辖域外经济增长“拐点”

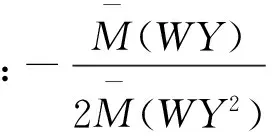
三、基于中国31省1990—2012年面板数据的实证检验

(一)数据指标

1.数据来源

由于废水和固体废物的空间扩散更多受制于地表环境以及人为因素的影响，因此考虑到污染物空间扩散的难易程度，本文选用最能体现污染物空间扩散的人均工业废气排放量(万立方米/人)作为实证研究的环境污染物指标，数据来源于《中国环境年鉴》。经济增长用1952年不变价衡量的人均GDP(元/人)代表，数据来源于《中国统计年鉴》。数据样本的各项统计指标表明各样本指标存在合理程度的变异，因此适宜回归使用。

2.空间权重矩阵

由于污染物空间扩散遵循“地理学第一定律”，即对污染源以外其他地区的污染强度随地理距离扩大而衰减，因此本文拟按k阶最近(Nearest)邻域数来设定空间权重矩阵。作法如下：以中国31省区为例，计算每一省与其他30省的地理距离，然后选取其中地理距离最近的k个省作为该省的毗邻区域，在空间权重矩阵当中相应位置设定元素值为1，其余30-k个省则不作为该省的毗邻区域，在空间权重矩阵当中相应位置设定元素值为0*空间权重矩阵为一N×N阶矩阵，矩阵当中的第一元素值均反映了任意两地区的地理毗邻关系，如矩阵当中第i行第j列的元素值(i≠j)则反映了地区样本当中i地区和j地区是否毗邻，如果毗邻则设定元素值为1，否则设定为0。矩阵主对角线上元素值全部设定为0，因为此时某一地区与自身重合。。由于大城市及其周边承担了所在地区经济发展重任，因此基于省会城市经-纬度坐标，采用Delauney三角剖分算法计算各省之间距离。由于中国各省所毗邻的省域数大都介于6～8个，因此，k阶最近邻域也分别按6～8来构建空间权重矩阵。设定完矩阵元素值后再进行标准化处理。

(二)模型设定形式的稳健性检验

前文基于“空间双拐点”假定推导得到的空间环境库兹涅茨曲线，其模型设定形式是否有别于经典线性环境库兹涅茨曲线及其另外两种空间模型设定形式，是实证验证“空间双拐点”假定的关键。就经典线性环境库兹涅茨曲线是否应扩展成空间模型，本文首先给出其是否应包含空间交互效应的检验结果。

1.线性环境库兹涅茨曲线遗漏空间交互效应的检验

表2给出了基于最近6阶邻域(W6)的估计结果。从中推测经典线性环境库兹涅茨曲线可能遗漏了空间交互效应：第一，经典线性环境库兹涅茨曲线无论是采用聚合模型还是其他三种固定效应设定形式，其空间交互效应的两种检验量——LM检验统计量和稳健LM检验统计量的估计值绝大多数均可在1%的置信度水平上拒绝样本数据当中“不包含空间滞后项和空间误差自相关项”的原假设，由此提示应当对经典线性环境库兹涅茨曲线嵌入可能遗漏掉的空间交互项，以包容辖域内环境污染与辖域外经济增长之间关系的刻画。而对截面和时期联合固定效应的检验结果也提示需在面板数据模型估计中同时考虑双向固定效应。第二，四种模型设定形式下的拟合优度均不高，尤其是设定形式较为准确的双向固定效应估计结果仅为0.047 2，由此提示在用线性模型拟合环境库兹涅茨曲线时，可能遗漏掉了比较重要的空间解释变量。第三，变换空间权重矩阵构建方式，基于最近7阶邻域和最近8阶邻域的检验结果均与此保持一致。

表2还显示在四种不同固定效应的设定形式下，估计结果均表明环境污染与经济增长之间的长期均衡关系呈现倒U形，这与绝大多数文献的估计结果保持一致；据此计算的经济增长“拐点”显示人均GDP大概在达到18 000～22 000元区间之后，工业废气污染水平便会开始显著下降。

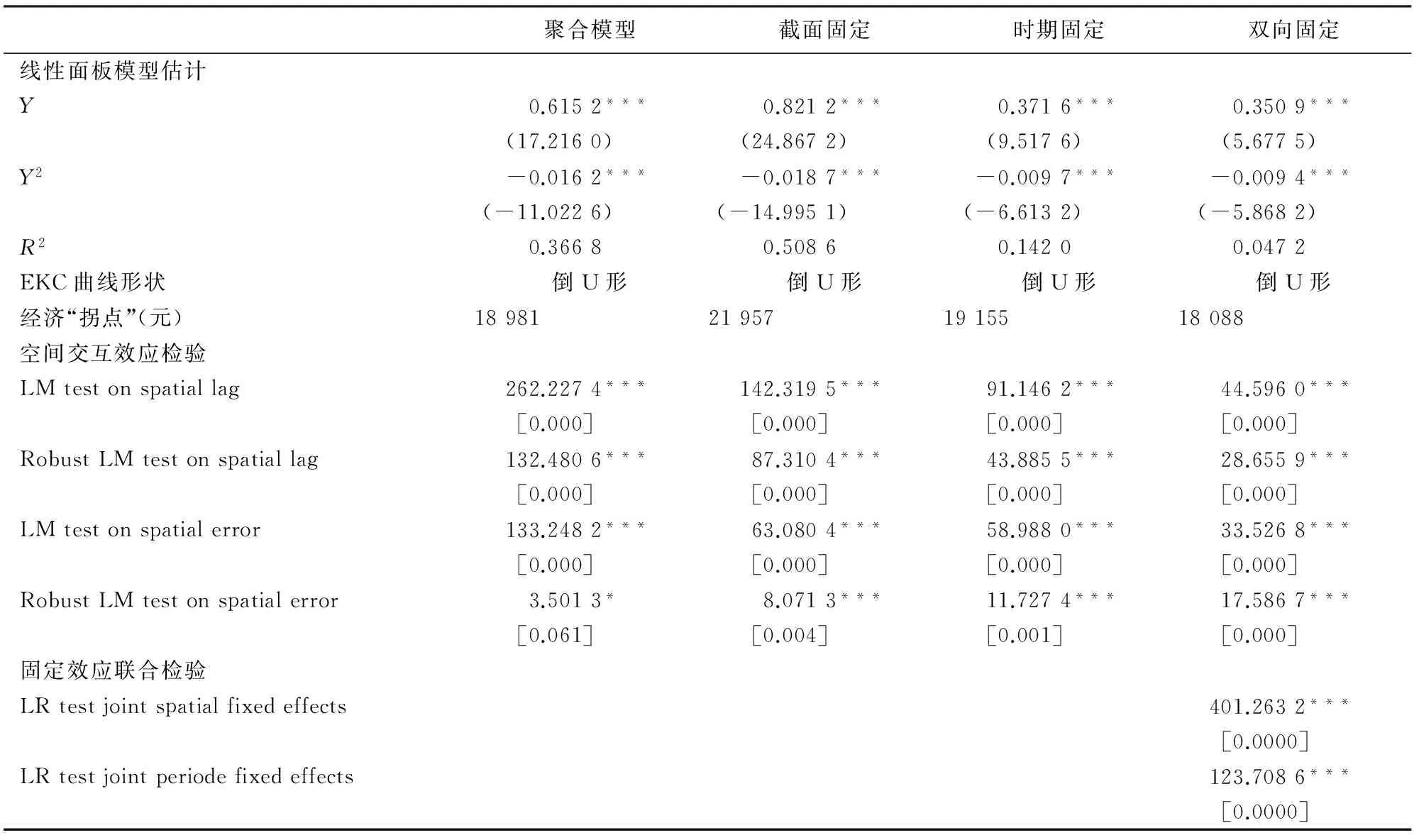
表2 线性环境库兹涅茨曲线估计及空间交互效应检验(W6)

注：省略常数项估计值；圆括号和方括号内分别为t值和p值；*、**、***分别代表在10%、5%、1%置信度水平上显著，下同。W6指基于最近6阶邻域的估计。

2. “空间双拐点”环境库兹涅茨曲线的稳健性检验

表2基于线性模型是否遗漏空间交互项的检验结果已表明需要将经典环境库兹涅茨曲线在空间维度进行扩展，这在一定程度上支持本文对环境库兹涅茨曲线空间建模的合理性，但推导所得到的“空间双拐点”环境库兹涅茨曲线在设定形式上是否与常用的两种空间模型存在实质性差异，这仍需要进行第二步检验(结果见表3)。

从表3空间模型估计结果不难发现，无论采用哪一种空间权重矩阵设定形式，空间模型的拟合优度均较之前线性模型的拟合优度要有了明显提升，其中固定效应模型拟合优度达到70%以上，随机效应模型拟全优度则为50%以上，表明空间交互解释变量的加入进一步全面了环境库兹涅茨曲线对经济增长与环境污染之间复杂关系的刻画。从代表污染物空间相关性的参数ρ的估计结果来看，无论哪种模型设定形式下，其估计值不仅为正而且均通过了置信度为1%的显著性检验，这就验证了之前绝大多数文献基于空间滞后模型和空间误差模型所得到的检验结论，即污染具有空间扩散属性。这也从另一方面说明突破以往线性模型所普遍遵循的“截面单元观测值彼此不相关”这一强假定而采用空间建模是较为科学的。

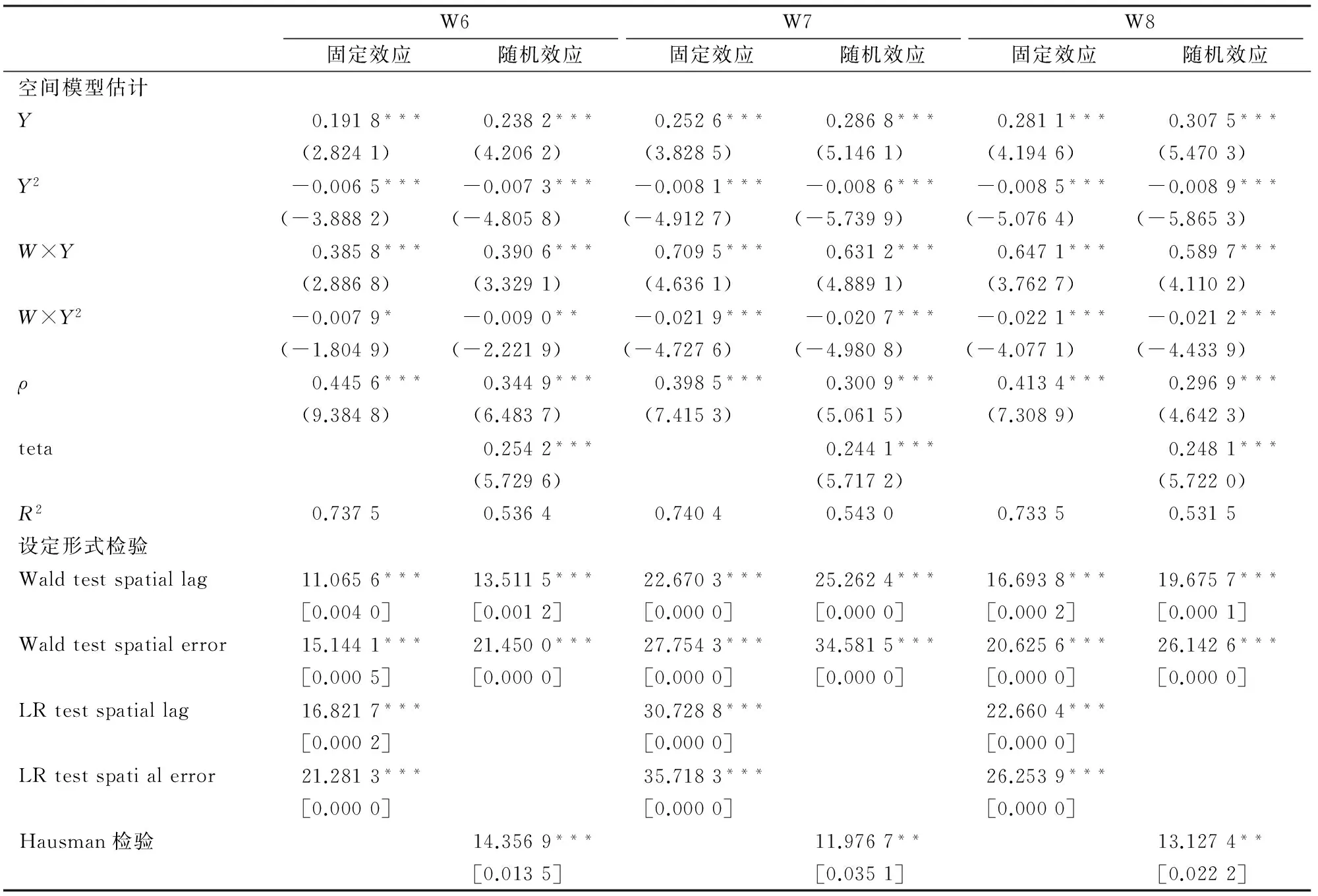
表3 “空间双拐点”环境库兹涅茨曲线的设定形式检验

注：随机效应设定形式下不支持针对原假设“SDM与SLM和SEM设定形式并无本质区别”的LR检验。W6、W7、W8分别代表最近邻域除数为6、7、8的空间权重矩阵，每一空间权重设定形式下均给出了截面单元为固定效应或随机效应的估计结果。

从表3设定形式检验结果不难发现，具有空间Durbin结构的“空间双拐点”环境库兹涅茨曲线退化成另外两种常用空间计量模型的Wald和LR检验结果均表明，可在1%的置信度水平上拒绝“空间Durbin结构可退化成空间滞后模型”以及“空间Durbin结构可退化成空间误差模型”的原假设。这就表明，实际面板样本的数据生成方式(DGP)更吻合于本文理论扩展所得到的“空间双拐点”环境库兹涅茨曲线，经济增长与环境污染之间的空间交互关系得到了验证。另外，Hausman检验结果表明无论采用哪一种空间权重矩阵设定形式，截面单元固定效应模型的设定形式优于随机效应设定形式。

(三)环境库兹涅茨曲线的“空间双拐点”计算

根据前文阐述，要计算空间环境库兹涅茨曲线的“空间双拐点”，首先必须基于偏矩阵法得到空间模型当中各解释变量对因变量影响系数的估计。表4首先按式(9)～式(10)给出人均GDP变量及其空间滞后项的估计值，进而计算出不同空间区域的经济“拐点”。

表4在3种空间权重矩阵情况下，分别给出了固定效应和随机效应设定形式下空间“双拐点”的计算结果。由于表3中Hausman检验结果表明应选用固定效应模型，因此基于固定效应模型的估计结果给出相应解释。结果表明无论是辖域内还量辖域外，人均GDP变量的参数估计值均大于0，而人均GDP变量平方项的估计值均小于0，这就说明辖域内大气污染同辖域内经济增长和辖域外经济增长之间的关系均是倒U形。

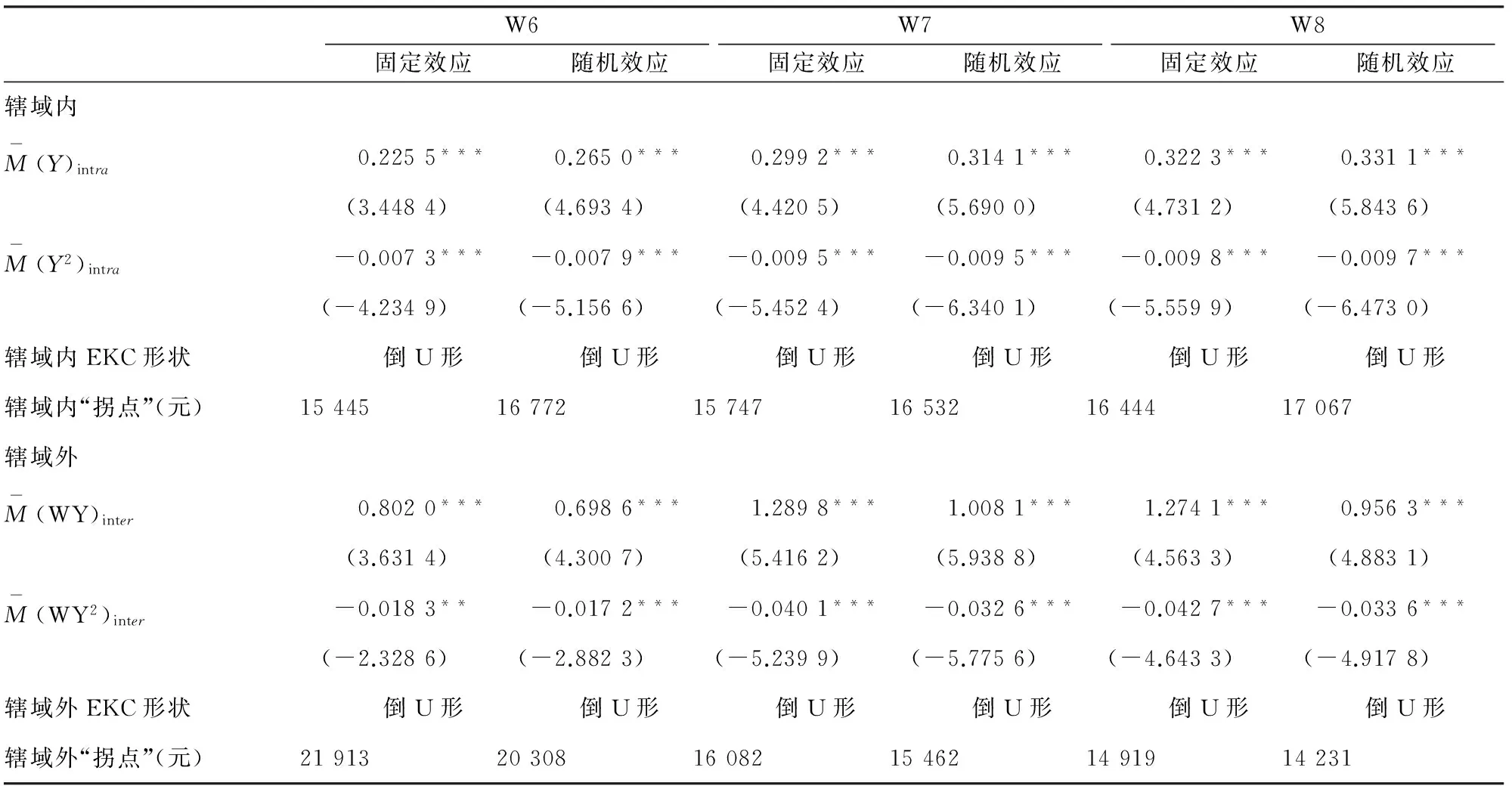
表4 “空间双拐点“计算

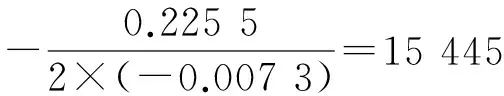
随着能够产生污染空间扩散的邻域数越来越多，对上述基于6阶邻域数得出的结论会产生何种影响？本文基于最近7阶邻域和最近8阶邻域的空间权重矩阵来对“空间双拐点”环境库兹涅茨曲线重新估计，发现：1.大气污染同辖域内外经济增长之间的长期关系较为稳定。估计结果显示无论采用哪一种空间权重矩阵设定形式，大气污染同辖域内外经济增长之间均呈现倒U形关系。2.随着能够产生污染空间扩散的邻域数不断增加，遏制大气污染所要求的辖域内经济“拐点”趋于严格。基于最近7阶邻域(W7)的估计结果显示，当产生污染空间扩散的毗邻地区数由6增加到7时，辖域内经济“拐点”则由原来最近6阶邻域的15 445元上升到15 747元，增幅302元；而当产生污染空间扩散的毗邻地区数由7增加到8时，辖域内经济“拐点”则由原来最近7阶邻域的15 747元上升到16 444元，增幅697元，增幅还呈上升趋势。这就表明随着污染源地区数目的不断增加，空间扩散至辖域内的污染增量也会不断上升，遏制大气污染所要求的经济发展水平也会进一步攀高。3.随着能够产生污染空间扩散的邻域数不断增加，遏制大气污染所要求的辖域外经济“拐点”随着地理距离延长而趋于宽松。基于最近7阶邻域(W7)的估计结果显示，当产生污染空间扩散的毗邻地区数由6增加到7时，辖域外(平均)经济 “拐点”则由原来最近6阶邻域的21 913元下降到16 082元，降幅5 831元；而当产生污染空间扩散的毗邻地区数由7增加到8时，辖域外(平均)经济 “拐点”则由原来最近7阶邻域的16 082元进一步降至14 919元，降幅1 163元，增幅还呈下降趋势。这说明随着产生污染空间扩散的邻域数不断增加，为扭转污染空间扩散影响，对遥远地区所要求的经济发展水平就比邻近地区要低，这主要是因为污染空间扩散存在地理衰减效应，符合“地理学第一定律”原旨。

四、结论及政策建议

考虑到空气污染物的强空间扩散属性，本文将传统线性的环境库兹涅茨曲线在空间维度扩展成具有空间Durbin结构的计量模型，同时涵盖大气污染与不同地区经济增长之间的长期关系。基于中国31省1990—2012年面板数据的实证研究发现：1.具有空间Durbin结构的“空间双拐点”环境库兹涅茨曲线，其空间模型设定形式较之文献当中常用的空间滞后模型和空间误差模型更适宜用来拟合实证样本的数据生成方式。2.大气污染同辖域内、外不同地区经济增长之间关系的估计结果符合经典环境库兹涅茨曲线所描述的倒U型关系，即使在变换不同空间权重矩阵设定形式后这一结论仍然稳健。3.随着能够产生污染空间扩散的毗邻地区数不断增加，大气质量改善所要求的辖域内经济发展“拐点”趋于严格；而大气质量改善所要求的辖域外其他地区经济发展“拐点”则随着地理距离延长而趋于宽松。

政策建议如下：1.污染治理需要中央集权式统筹管理。本文检验结果再一次证实大气污染的强空间扩散属性，因此地区间污染治理需要协同性和高度一致性，这个角色就只能由中央政府来扮演。2.缩减地区间收入差距至合理区间。本文检验结果证实大气污染与辖域内、外经济增长之间皆呈倒U型关系，并且大气质量改善对辖域外地理距离越近地区的经济发展水平要求也就越高。因此，以往过分关注某一地区经济结构调整的政策需要适时调整，否则就难以顾及到周边欠发达地区落后经济增长方式所带来的污染空间扩散危害。3.重视对传统产业的技术升级改造，而非单纯区域间转移。本文检验结果证实污染空间扩散来自污染源所在地区低劣的经济增长水平，因此，产业输出地单纯的落后产业转移行为并不能有助于所在辖域空气质量的提升，反而会对输出地提出更为苛刻的人均收入增长要求。完全淘汰过剩产能和落后产业，或是强化技术革新改造，才是改善环境质量的根本出路。

[1] Grossman G M, Krueger A B. Environmental Impacts of the North American Free Trade Agreement[C]. NBER, Dordrecht: Working Paper, 1991.

[2] 王立平，管杰，张纪东.中国环境污染与经济增长：基于空间动态面板数据模型的实证分析[J].地理科学，2010，30(6).

[3] Anselin L, Getis A. Spatial Statistical Analysis and Geographic Information Systems[J]. Annals of Regional Science, 1992, 26(1).

[4] Poon Jessie P H, Casas I, He C. The Impact of Energy, Transport, and Trade on Air Pollution in China[J]. Eurasian Geography and Economics, 2006, 47(5).

[5] Rupasingha A, Goetz S J, Debertin D, Pagoulatos A. The Environmental Kuznets Curve for US Counties: A Spatial Econometric Analysis with Extensions[J]. Papers in Regional Science, 2004, 83(2).

[6] Anselin L. Spatial Effects in Econometric Practice in Environmental and Resource Economics[J]. American Journal of Agricultural Economics, 2001, 83(3).

[7] Maddison D. Modelling Sulphur Emissions in Europe: A Spatial Econometric Approach[J]. Oxford Economic Papers, 2007, 59(4).

[8] Hosseini H M, Rahbar F. Spatial Environmental Kuznets Curve for Asian Countries: Study of CO2and PM2.5[J]. Journal of Environmental Studies, 2011, 37(9).

[9] Hossein H M, Kaneko S. Can Environmental Quality Spread through Institutions[J]. Energy Policy, 2013, 56(5).

[10]张可，汪东芳.经济集聚与环境污染的交互影响及空间溢出[J].中国工业经济，2014(6).

[11]马丽梅,张晓.中国雾霾污染的空间效应及经济、能源结构影响[J].中国工业经济，2014(4).

[12]沈能,周晶晶,王群伟.考虑技术差距的中国农业环境技术效率库兹涅茨曲线再估计：地理空间的视角[J].中国农村经济，2013(12).

[13]Zhang Q，Felmingham B. The Role of FDI, Exports and Spillover Effects in the Regional of China[J]. Journal of Development Studies, 2002, 38(4)．

[14]Groenewold N, Lee G， Chen A. Regional Output Spillovers in China: Estimates from a VAR Model[J]. Papers in Regional Science, 2007, 86(1).

[15]潘文卿.中国的区域关联与经济增长的空间溢出效应[J].经济研究，2012(1).

[16]Parent O，LeSage JP. Using the Variance Structure of the Conditional Autoregressive Specification to Model Knowledge Spillovers[J]. Journal of Applied Econometrics, 2008, 23(2).

[17]孙圣民.制度变迁与经济绩效关系研究新进展[J].经济学动态，2008(10).

[18]刘超.管制、互动与环境污染第三方治理[J].中国人口·资源与环境，2015(2).

[19]Elhorst J P. Matlab Software for Spatial Panels[J]. International Regional Science Review, 2012, 8(1).

[20]LeSage James， Pace R Kelley. Introduction to Spatial Econometrics[M]. New York: CRC Press, 2009.

(责任编辑：马 慧)

Re-estimating Environmental Kuznets Curve with Two Spatial Break Points

LIU Shun-jia

(Business School, Hunan Agriculture University, Changsha 410128, China)

The classical linear Environmental Kuznets Curve is developed with two spatial break points which can analyzes relationship between environmental pollution and local economic growth, even relationship between environmental pollution and neighbor economic growth. By using a panel data including Chinese 31 provinces from 1990 to 2012 , the test shows that relationship of reverse U-shaped curve is depicted between environmental pollution and local economic growth, that is same to relationship between environmental pollution and neighbor economic growth. The conclusion is robust even using different spatial weighted matrix. So the environmental pollution can be suppressed only when both spatial break points are achieved. Along with polluting districts increasing, local economy development level has to be promoted to suppress pollution, which causes local break point of economic growth to be late to reach. Even lower economy development level of neighbor district can match the request of local pollution treatment when distance between them is extended. So it suggests that pollution must be treated by central government, with reducing economic gap between developed areas and developing areas, stopping industrial transfer among areas.

spatial break point；Environmental Kuznets Curve；spatial diffusion

2015-04-24

湖南农业大学国际经济与贸易专业重点学科、湖南农业大学商学院龙头项目《家庭农场的生成路径及成长性绩效研究》，湖南农业大学商学院涉农研究中心资助。

刘舜佳，男，湖南茶陵人，副教授，国际经济与贸易专业博士，研究方向：知识空间溢出。

F061.5

A

1007-3116(2015)11-0063-09