弹道中段带翼弹头章动微多普勒特性研究

姚汉英，李星星，孙文峰，马晓岩

(1.空军预警学院研究生管理大队， 武汉430019;2.解放军94878部队， 安徽芜湖241000)

0 引言

弹头在弹道中段惯性飞行时，需要采用自旋运动进行姿态控制以保证其能够小攻角再入和提高命中精度。同时，受重力矩作用，弹箭分离、诱饵释放及其他外部扰动的影响，会在自旋的基础上产生锥旋和摆动，进而形成进动和章动等微运动，这会引起雷达回波的多普勒调制和功率调制，其中，引起的多普勒调制称为微多普勒效应［1］。美国海军研究实验室 Victor C.Chen［2-3］首次将微多普勒概念引入雷达探测领域，并系统研究了微运动和微多普勒现象，对刚体目标旋转所产生的微多普勒进行了理论分析与研究。这为弹道中段目标特征提取及识别提供了新的途径，也成为了弹道中段目标特性研究的热点领域［4-9］。文献［10］通过微波暗室动态测量实验有效地观测了进动锥体目标的微多普勒特性，并分析了进动目标滑动型散射中心的微多普勒;文献［11-13］在对带翼弹头进动微多普勒研究的基础上，通过建立弹头章动数学模型，在理想点散射模型假设下，利用微动矩阵理论对弹道目标的章动微多普勒进行了仿真与分析。本文以典型的带翼锥体弹头为研究对象，建立了章动数学模型，依据带翼弹头的主要散射机理，改进以往固定不变的理想点散射模型，除面散射以外，将带翼弹头主要散射类型分为固定型和滑动型点散射中心两大类，并考虑尾翼的遮挡效应，分别推导了这两类点散射中心的章动微多普勒公式。基于电磁计算软件获取目标的静态电磁散射数据，模拟了带翼弹头的章动微多普勒现象，验证了理论微多普勒公式的正确性，并给出了一些重要结论。尤其是本文在此通过理论分析和仿真实验验证了带翼弹头进动或章动时尾翼散射中心包络内部微多普勒变化频率与自旋和锥旋频率均有关，修正了前面学者认为其仅与自旋频率有关的结论［11，13］。

1 带翼锥体弹头章动模型

自旋、锥旋和摆动的组合运动即产生弹头的章动，描述章动的主要参数有自旋频率、锥旋频率、锥旋角、摆动频率和摆动幅度［14］。假设弹头为带翼锥体目标，以目标质心(目标轴线与锥旋轴线的交点)为原点建立弹道中段目标章动模型，如图1所示。图中目标锥旋轴为Oz轴，锥旋轴与雷达视线确定的平面为yOz平面，再根据右手定则建立Oxyz参考坐标系。设Ox'y'z'为弹体坐标系，Oz'轴为目标的旋转对称轴，x'Oz'平面平行于锥体底面，Ox'轴指向初始方位，弹头绕其对称轴Oz'以角速度ωs做自旋运动，同时Oz'轴绕Oz轴以角速度ωc做锥旋运动，锥旋角为 θc，对称轴 Oz'以角速度ωc和幅度θw做摆动，ϑ为雷达视线相对弹道目标锥旋轴的夹角。于是俯仰角β为雷达视线与Oz'轴的夹角，方位角α为雷达视线在 x'Oy'平面上的投影与Ox'轴的夹角。图中A、B和C三点为下文将要介绍的三个点散射中心类型。

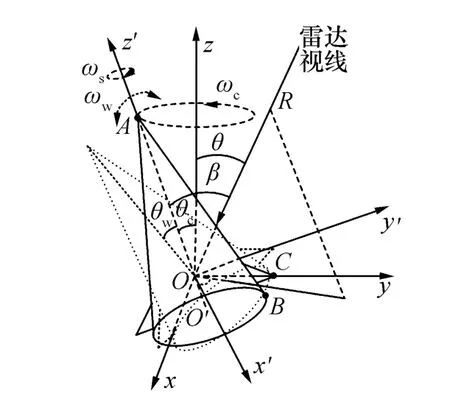
图1 带翼弹头章动模型

设t时刻锥体轴线在参考坐标系xOy平面内的相位角为φc=ωct+φc0，φc0为零时刻弹头顶部轨迹的圆心到弹头顶部连线与x轴的夹角，章动角是其与锥旋轴 Oz的夹角 θn=θc- θwsinφw，φw=ωwt+ φw0，φw0弹头摆动的初始相角。弹头自旋在x'Oy'平面内扫过的相角为φs=ωst+φs0，φs0为零时刻的初始相角。由空间直角坐标系的旋转变换关系，参考坐标系Oxyz到弹体坐标系O'x'y'z'的旋转变换矩阵为

其中

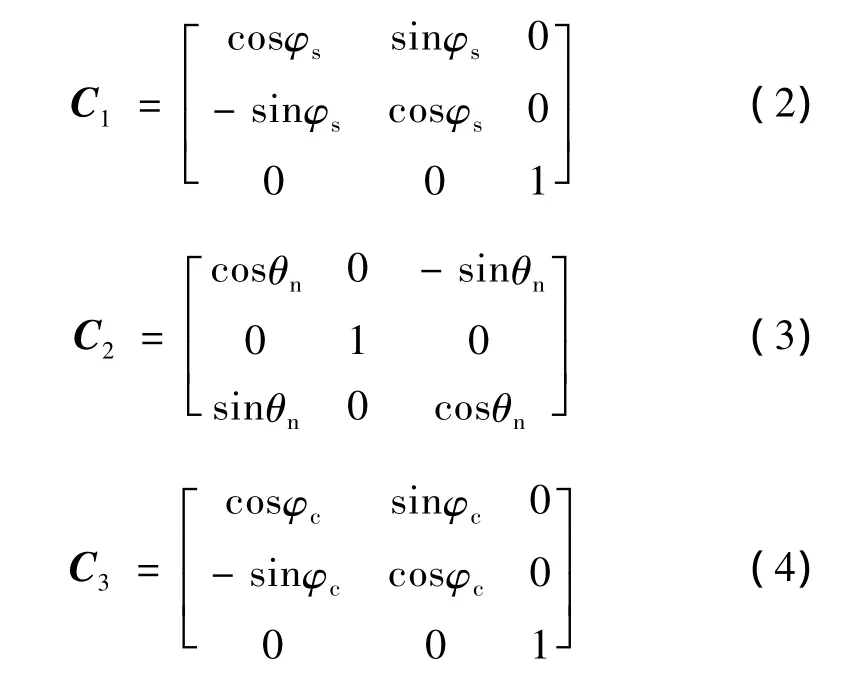
于是旋转变换矩阵R可以化简为

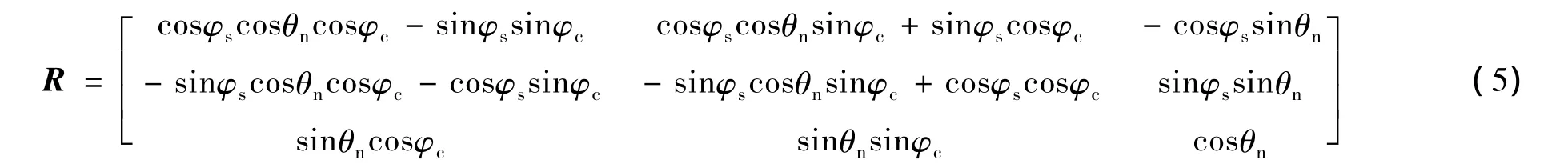
在Oxyz坐标系中，雷达视线的反方向单位矢量可表示为 er=(0，sinϑ，cosϑ)T，则其在弹体坐标系中可表示为

式中:ez'［0 0 1］T为坐标系 Ox'y'z'中 Oz'轴方向的单位矢量。式(7)中当 sinφc=1 时，β =|ϑ -θn|，当 sinφc=-1时，β=ϑ+θn，可见俯仰角的变化范围取决于雷达视线角和章动角，由于章动角是随时间摆动变化的，因此，章动时短时间内俯仰角的变化是在雷达视线角以锥旋角为幅度振荡的基础上调制了摆动角的变化。

同样，从式(6)可获得方位角的正切函数为

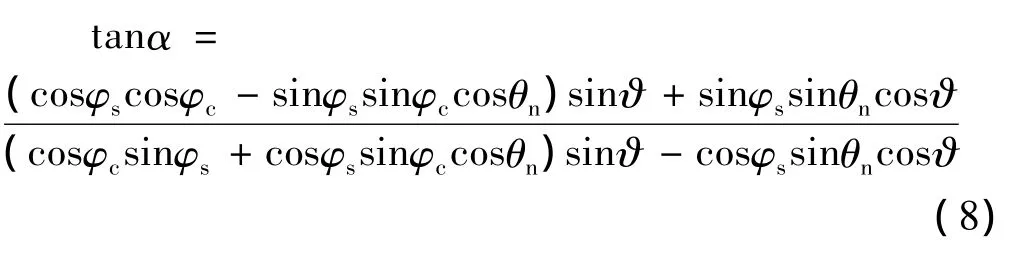
由式(8)可见，方位角较俯仰角更为复杂，为了后面更好地对弹头尾翼章动微多普勒特性进行分析，下面对方位角做如下讨论。当章动角θn较小时，式(8)可近似为

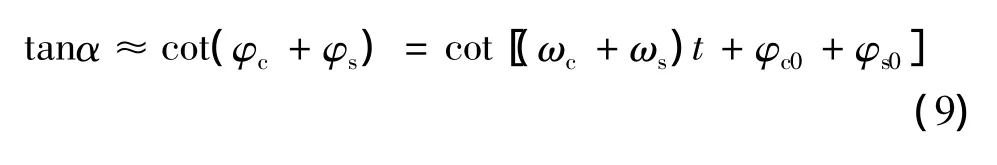
从式(9)可以看出，当章动角较小时，方位角的变化角速度为自旋和锥旋角速度之和(ωp+ωs)，即方位角的变化频率为自旋和锥旋频率之和。

2 带翼弹头章动微多普勒理论分析

一般而言，弹头形状比较简单，多为旋转对称体或有翼对称体。在地基X波段雷达体制下，若不考虑特定姿态角下目标的面散射，仅考虑其点散射中心时，依据目标的电磁散射机理，在此可将其点散射中心类型分为两大类，即固定型点散射中心和滑动型点散射中心［10］。固定型点散射中心是指目标上的散射中心在目标坐标系中的相对位置是固定不变的，如常见带翼弹头顶部及尾翼尖顶的散射(图1中A点和C点);滑动型点散射中心指目标上的散射中心在目标坐标系中的相对位置是滑动变化的，如常见弹头的底部边缘及不连续环处的电磁散射(图1中B点)。下面对两类点散射中心的微多普勒公式进行理论推导。

2.1 固定型点散射中心微多普勒分析

设质心为参考点，式(6)中雷达视线在弹体坐标系中单位方向矢量为er'=［A(t)B(t)C(t)］T，坐标系Ox'y'z'中点X的矢量坐标可以表示为rX'=［xX'yX'zX'］T，其在雷达视线方向上的投影距离为

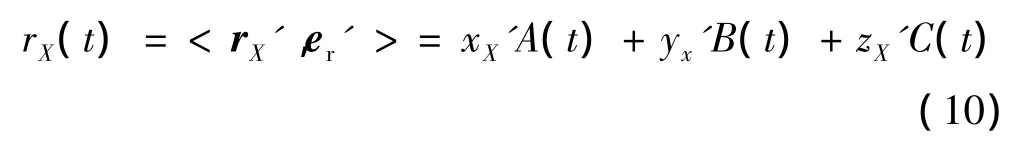
式中:＜·，·＞表示对两个矢量求内积。

于是，点X对应的微多普勒公式可表示为

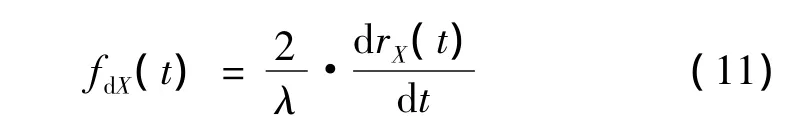
式中:λ为波长，对于一般固定型点散射中心而言，其章动微多普勒与摆动、自旋和锥旋参数均有关。下面针对带翼弹头，主要对两种固定型点散射中心进行分析。

2.1.1 顶部固定型点散射中心

对于顶部点散射中心A有rA'=［xA'yA'zA'］T，其中xA'=yA'=0，结合式(10)和式(11)可得顶部点散射中心A的微多普勒为

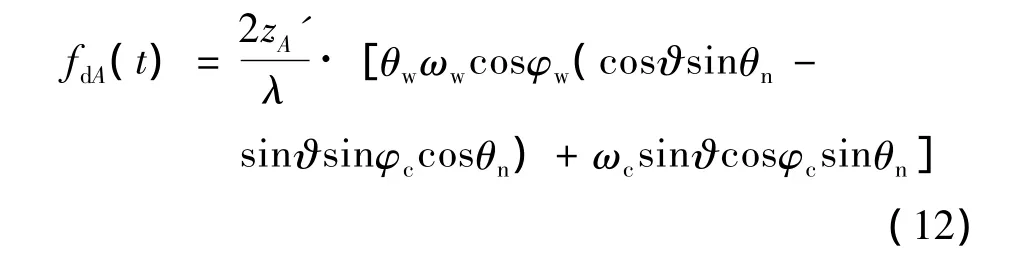
由式(12)可见，顶部点散射中心的章动微多普勒主要受摆动及锥旋运动参数的影响，与自旋参数无关，且章动微多普勒周期是摆动周期和锥旋周期调制的结果。

若 θw=0，此时有

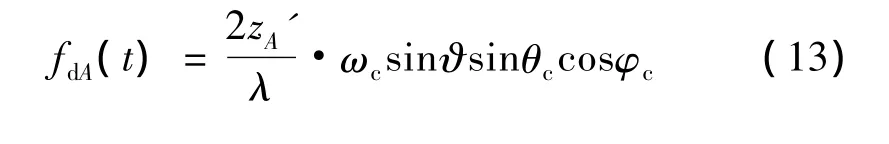
即在弹头进动情况下，顶部散射中心的微多普勒呈正弦规律变化，变化周期与锥旋周期一致，这与文献［10］的分析结果是一致的。

2.1.2 尾翼固定型点散射中心

对于尾翼点散射中心 C，有rC'=［xC'yC'zC'］T，设其在雷达视线方向上的投影距离为rC(t)。考虑其方位上的遮挡现象，带翼锥体弹头尾翼固定散射中心遮挡示意图如图2所示，设翼尖为其强散射点，其均在图中S、C、E三点构成的圆环上，Q为圆心，与其在同一平面内的内部圆环为平面SCE与锥体表面的交线，由图1中方位角的定义，在C处雷达视线方位角为90°，则C处尾翼被遮挡的时刻对应雷达视线方位角在小圆弧S⌒E段，此时SS'刚好与内圆环外切，∠S'QC=90°，φ可依据带翼弹头的尺寸获得，于是可得尾翼固定散射中心C的微多普勒为

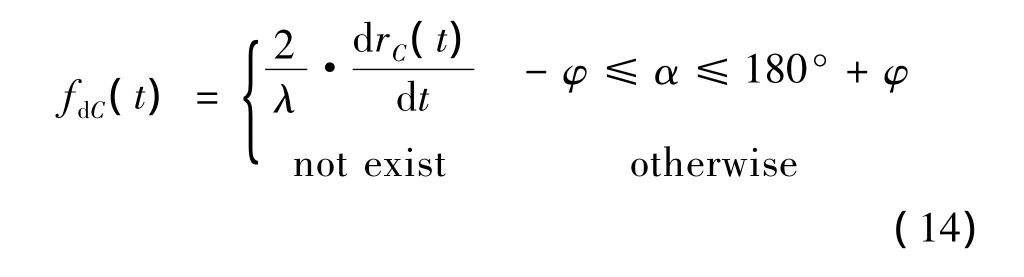
同理，依据其他尾翼固定型散射中心初始相角的不同，亦可分析其对应的微多普勒遮挡情况。

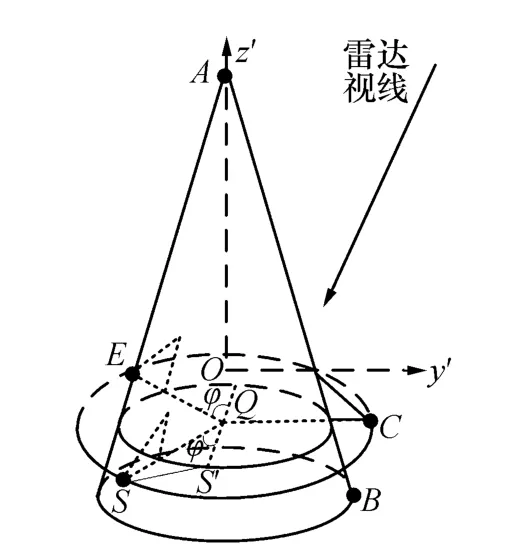
图2 带翼弹头遮挡效应

2.2 滑动型点散射中心微多普勒分析

边缘滑动型点散射中心为电磁波入射方向与目标旋转对称轴所构成的平面与底部边缘的交点，任一时刻其在坐标系Ox'y'z'中的位置是变化的，设其坐标为rB'(t)=［xB'(t)yB'(t)zB'(t)］T，则雷达视线与 z'轴构成的平面方程为

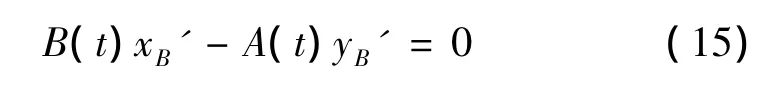
由于散射点在边缘滑动，设其到质心的水平距离为 RB，则有

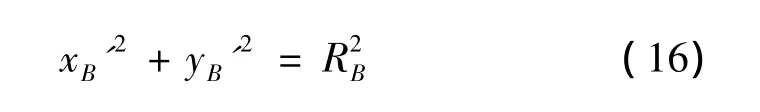
联立式(15)和式(16)，可解得

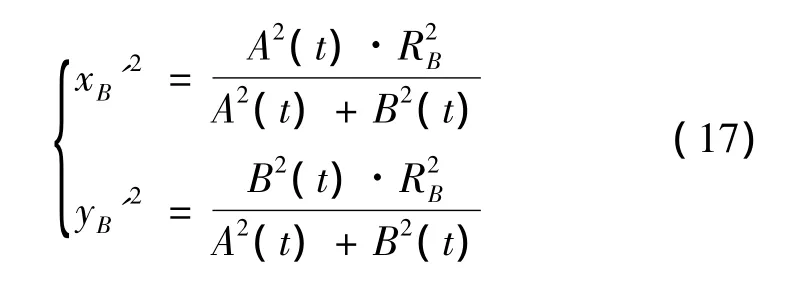
因在坐标系Ox'y'z'中滑动型点散射中心B的坐标zB'(t)是不变的，即其距质心的垂直距离为|zB'|，则其在雷达视线方向上的投影距离为

由式(21)可知，进动情况下其微多普勒变化除了一个余弦形式变化外，还有一个受实时姿态角余切函数调制的余弦波形，这会导致其微多普勒偏离正弦规律变化，与文献［10］分析也是一致的。

3 仿真与分析

为验证上述章动微多普勒公式的正确性，建立带翼锥体弹头的CAD模型如图3所示。图中，锥体高度为2.7 m，底面半径为0.7 m，半锥角为ε=14.53°，弹头质心位置O距底部高度为0.7 m，弹头的四个尾翼均是一样的，尾翼长0.4 m，高0.55 m，厚度0.05 m。为避免锥面、尾翼平面以及二者构成的二面角等强散射中心的出现，假设此处研究的目标俯仰角范围为［ε，π/2-ε］，这也是雷达探测目标的常见俯仰角范围，此时在章动情况下带翼锥体弹头的主要散射特性为顶部及四个尾翼对应的固定型点散射中心以及底部边缘滑动型点散射中心。设雷达的工作中心频率为10 GHz，脉冲重复频率为800 Hz，由于地基雷达相对目标距离较远，故短时间内可以认为雷达视线角是不变的，设平均视线角为60°。为方便理论仿真分析时微多普勒曲线的观察，设弹头顶部散射中心的散射强度为其他散射中心散射强度的两倍，弹头各尾翼被遮挡的视线角范围为240°。弹头章动微多普勒仿真时章动参数(包括自旋角速度ωs、锥旋角 θc、锥旋角速度 ωc、摆动幅度θw和摆动角速度)的设置如表1所示(此处参数设置主要为验证章动微多普勒的一些特性)。基于假设的带翼弹头各散射中心在弹体坐标系中的坐标位置，利用第2节中推导的理论微多普勒公式，应用短时傅里叶变换对目标的微多普勒进行理论仿真，得到不同章动参数情况下章动微多普勒理论仿真结果，如图4a)～图4f)所示。

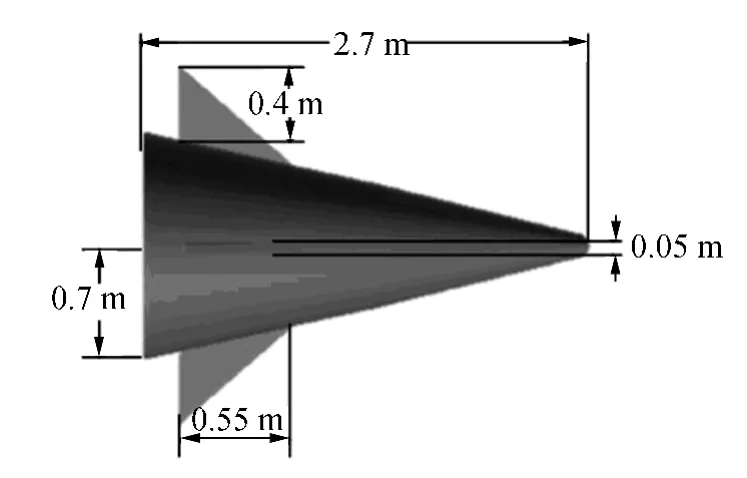
图3 带翼锥体弹头CAD模型

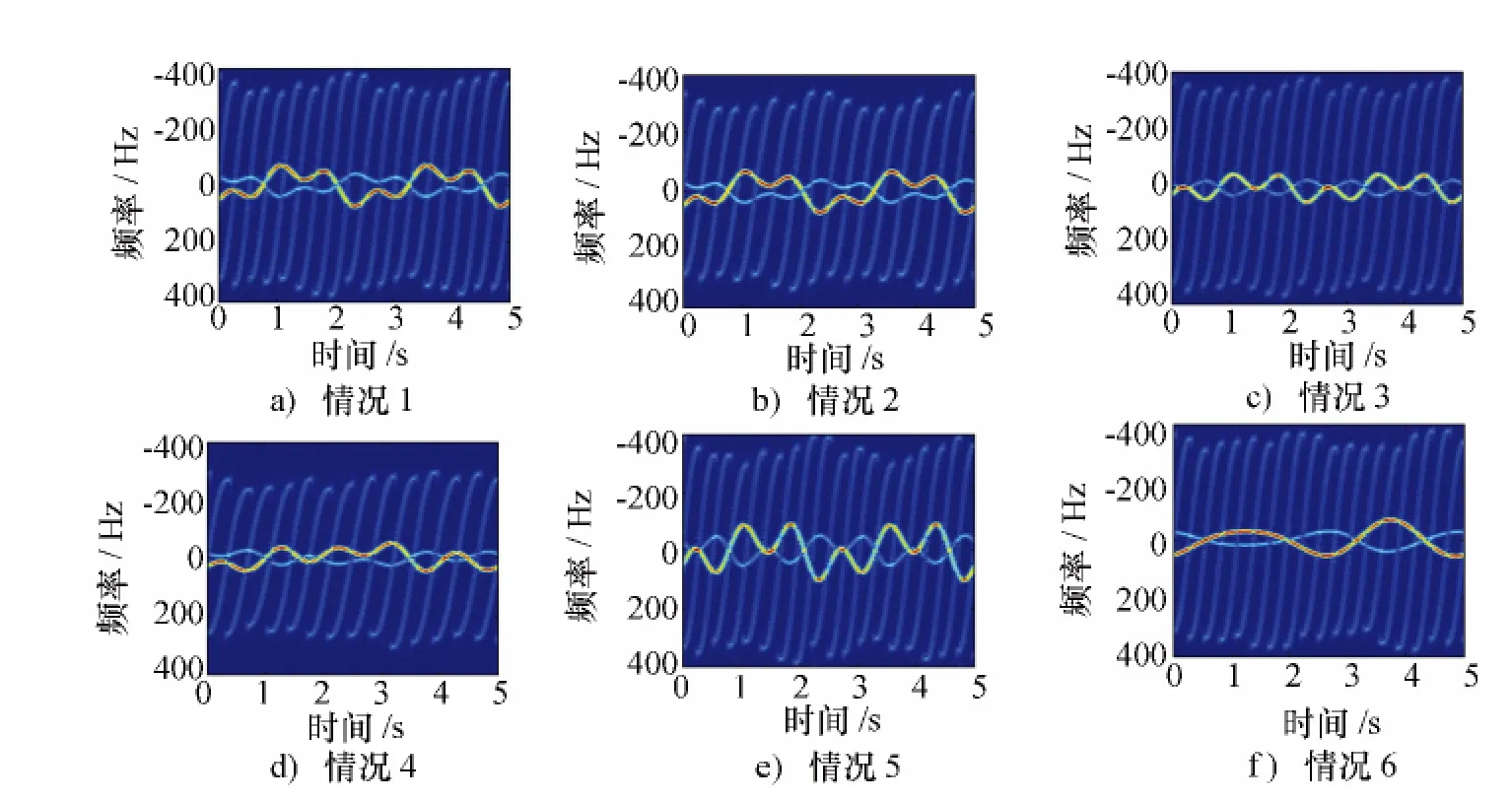
图4 章动微多普勒理论仿真结果

为比较分析带翼弹头章动微多普勒与进动微多普勒的异同，在雷达平均视线角仍为60°时，图5显示了表1中第1种情况下不考虑摆动，即在进动时的微多普勒曲线。

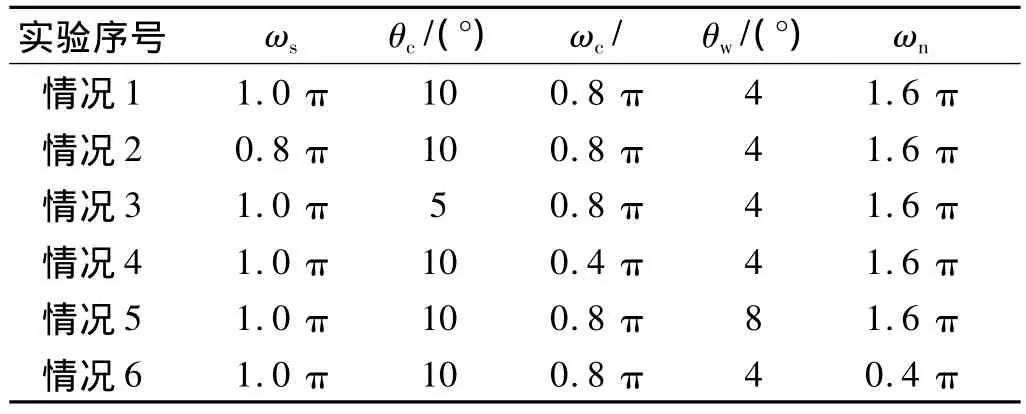
表1 目标章动微多普勒仿真参数 rad·s-1

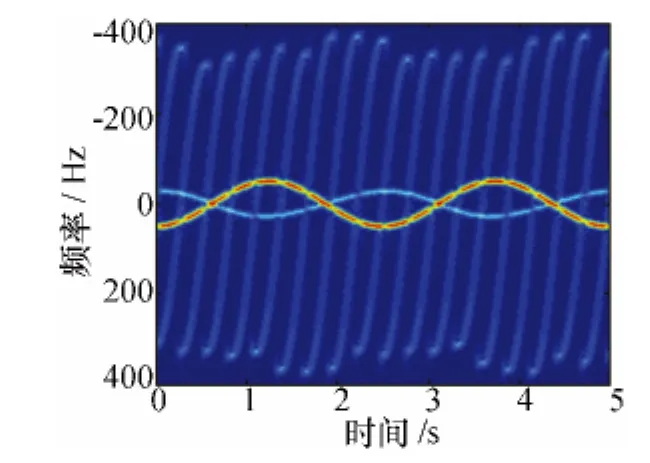
图5 进动微多普勒理论仿真结果

通过比较分析图4中带翼弹头在不同章动参数情况下的章动微多普勒理论仿真结果以及图5中进动微多普勒理论仿真结果，可以得出以下6点结论:

1)从总体上看，由尾翼散射中心进动和章动产生的微多普勒幅度要比顶部散射中心和边缘散射中心产生的微多普勒幅度大，这更有利于地基雷达对微多普勒的观测。

2)通过比较图4a)和图4b)可知，目标自旋对顶部和底部边缘散射中心的微多普勒以及尾翼产生的微多普勒包络形状均没有影响，但其对尾翼产生的包络内部微多普勒幅度及周期影响较大，这与理论微多普勒公式的分析是一致的。

3)由图4a)、图4c)和图4d)可以发现锥旋角对各散射中心的微多普勒曲线周期无影响，但对其幅度有一定影响、而锥旋频率对各散射中心的微多普勒曲线幅度和周期均影响较大。

4)由图4a)、图4e)和图4f)和图5可知带翼弹头章动的微多普勒幅度在进动微多普勒幅度的基础上增加了摆动的调制。摆动幅度和摆动频率均会影响各散射中心微多普勒曲线的形状，但摆动幅度不会影响其变化的周期，而摆动频率会对顶部和底部边缘散射中心的微多普勒以及尾翼产生的微多普勒包络的变化周期有一定影响。

5)由图4a)、图4d)和图4f)可知弹头顶部散射中心和底部边缘滑动散射中心的微多普勒以及尾翼微多普勒包络的变化周期都是一致的，其值等于锥旋周期和摆动周期的最小公倍数，与自旋周期无关。

6)对于带有4个尾翼弹头的尾翼微多普勒曲线包络内部变化频率近似为自旋频率与锥旋频率之和的4倍，与摆动频率无关，与理论分析一致。如图4a)和图4f)中尾翼的微多普勒断续出现18次，故变化频率为18/5=3.6(Hz)，其值刚好等于4×(0.5+0.4)=3.6(Hz)，同样，图4d)中有14/5=4 ×(0.5+0.2)(Hz)。

根据表1中第1种情况下的章动参数设置值，利用图3中建立的带翼弹头CAD模型，基于电磁仿真计算获取的目标电磁散射特性数据，在雷达平均视线角分别为30°和60°时得到的章动微多普勒的电磁仿真结果，如图6所示。图6a)中在雷达平均视线角为30°时，能明显看出各散射中心的微多普勒变化曲线，尾翼由于存在遮挡效应，其微多普勒曲线断续出现。图中弹头顶部和底部边缘散射中心的微多普勒以及尾翼微多普勒包络的变化周期均是一致的，为锥旋周期与摆动周期的最小公倍数2.5 s，包络内部尾翼产生的微多普勒曲线虽较模糊，但其断续出现18次，对应的变化频率为18/5=3.6(Hz)，恰好等于自旋频率与锥旋频率之和的四倍，这均与理论分析一致。

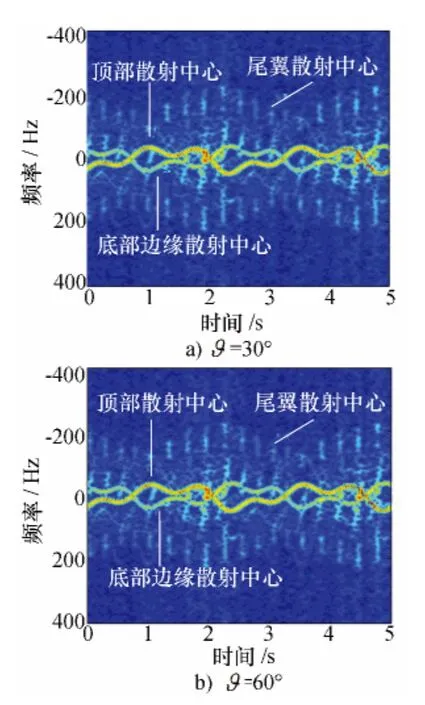
图6 章动微多普勒电磁仿真结果

图6b)为雷达平均视线角为60°时带翼弹头的章动微多普勒电磁仿真结果，与图6a)相比可知，随着视线角的增大，弹头章动的微多普勒幅度增大，这时对雷达工作的脉冲重复频率要求较高，否则会出现微多普勒模糊。比较图4a)和图6b)在相同条件下目标章动微多普勒的理论仿真结果和电磁仿真结果，二者总体的微多普勒曲线变化形式是相同的，微多普勒幅度及变化的周期均与理论分析一致。电磁仿真结果的微多普勒曲线较为模糊且明暗相间，尾翼散射中心的微多普勒包络与理论仿真差异较大，这是因为实际中带翼弹头各类散射中心的散射强度及尾翼的遮挡范围均是随姿态角变化的，所以电磁仿真结果更能反映带翼弹头电磁散射的真实情况。

4 结束语

章动是弹道中段弹头典型的微动形式之一，对其微多普勒特性的研究，可为弹道目标特征提取及识别提供新的途径。本文以一般的带翼锥体弹头为研究对象，通过理论推导获取的章动微多普勒公式和静态电磁散射数据模拟的雷达回波，分别得到了带翼章动目标微多普勒的理论和电磁仿真结果，通过比较分析验证了理论公式的正确性，总结了自旋频率、锥旋角、锥旋频率、摆动幅度和摆动频率对目标各散射中心章动微多普勒的影响情况，这对于弹道目标章动特性的模拟、特征参数反演及弹道防御系统中地基雷达的设计要求均具有一定的指导意义。

［1］庄钊文，刘永祥，黎 湘.目标微动特性研究进展［J］.电子学报，2007，35(3):520-525.Zhuang Zhaowen，Liu Yongxiang，Li Xiang.The achievements of target characteristic with micro-motion［J］.Acta E-lectronic Sinica，2007，35(3):520-525.

［2］Chen V C.Micro-Doppler effect in radar phenomenon，model，and simulation study［J］.IEEE Transactions on Aerospace and Electronic Systems，2006，42(1):2-21.

［3］Chen V C.The micro-Doppler effect in radar［M］.Boston:Artech House，2011.

［4］Schultz K，Davidson S，Stein K，et al.Range Doppler laser radar for midcourse discrimination:the firefly experiments［R］.［S.l.］:AIAA Press，1993.

［5］Liu L H ，Mclernon D，Ghogho M，et al.Ballistic missile detection via micro-Doppler frequency estimation from radar return［J］.Digital Signal Processing，2012，22(1):87-95.

［6］Niu J，Zhu Y P，Liu Y X，et al.Radar micro-motion feature extraction of cone target based on Hilbert-Huang transform［C］//IEEE International Conference on Information Science and Technology.Wuhan， China:IEEE Press，2012:401-404.

［7］姚汉英，孙文峰，马晓岩.基于高分辨距离像序列的锥柱体目标进动和结构参数估计［J］.电子与信息学报，2013，35(3):537-544.Yao Hanying，Sun Wenfeng，Ma Xiaoyan.Precession and structure parameters estimation of cone-cylinder target based on the HRRPs［J］.Journal of Electronics&Information Technology，2012，35(3):537-544.

［8］罗 迎，柏又青，张 群，等.弹道目标平动补偿与微多普勒特征提取方法［J］.电子与信息学，2012，34(3):602-608.Luo Ying，Bai Youqing，Zhang Qun，et al.Translational motion compensation and micro-Doppler feature extraction of ballistic targets［J］.Journal of Electronics&Information Technology，2012，34(3):602-608.

［9］田巳睿，蒋跃红，郭汝江，等.基于时频变换的弹道目标微多普勒特征提取［J］.现代雷达，2012，34(1):40-43.Tian Sirui，Jiang Yuehong，Guo Rujiang，et al.Ballistic target micro-Doppler feature extraction method based on the time-frequency analysis［J］.Modern Radar，2012，34(1):40-43.

［10］马 梁，刘 进，王 涛，等.旋转对称目标滑动型散射中心的微Doppler特性［J］.中国科学:信息科学，2011，41(5):605-616.Ma Liang，Liu Jin，Wang Tao，et al.Micro-Doppler characteristics of sliding-type scattering center on rotationally symmetric target［J］.Science in China:Information Sciences，2011，41(5):605-616.

［11］Gao H W，Xie L G，Wen S L，et al.Micro-Doppler signature extraction from ballistic target with micro-motions［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46(4):1969-1982.

［12］孙照强，李宝柱，鲁耀兵.弹道目标章动特性及其微多普勒研究［J］.现代雷达，2009，31(4):24-27.Sun Zhaoqiang，Li Baozhu，Lu Yaobing.A study on nutation property of ballistic target and its micro-Doppler［J］.Modern Radar，2009，31(4):24-27.

［13］孙照强，李宝柱，鲁耀兵.弹道中段进动目标的微多普勒研究［J］.系统工程与电子技术，2009，31(3):538-540.Sun Zhaoqiang，Li Baozhu，Lu Yaobing.Research on micro-Doppler of ballistic midcourse target with precession［J］.Systems Engineering and Electronics，2009，31(3):538-540.

［14］Huixia S，Zheng L.Nutation feature extraction of ballistic missile warhead［J］.Electronics Letters，2011，47(13):770-772.