掩护突防中雷达干扰无人机压制干扰航路优选

李子杰，刘湘伟，廖文龙，卢 高

(1.电子工程学院软件测评中心， 合肥230037;2.解放军77108部队， 四川崇州611233)

0 引言

近年来在局部战争中，无人机的使用几乎贯穿整个作战过程，其对战争行动的影响已经远远超过了人类的想象。雷达干扰无人机作为其中之一，在掩护突防作战、夺取战场制信息权行动中发挥了无与伦比的作用。雷达干扰无人机是以雷达干扰机为载荷、按照预先规划或临时指定航路飞行的、能够对目标雷达实施噪声压制或假目标欺骗干扰的一种电子战无人机［1］。目前，针对雷达干扰无人机的分析与研究方兴未艾，文献［2］从技术层面分析了雷达干扰无人机的干扰技术及干扰效果;文献［3-5］分析了不同作战背景下的电子战无人机运用，但并未予以定量研究;文献［6］对实施假目标干扰的无人机系统作战效能进行了定量分析。从已经发表的文献资料来看，针对执行压制干扰任务的雷达干扰无人机的作战运用定量分析较少。

遂行压制干扰任务时，雷达干扰无人机只能在相对较小空域内对雷达实施有效干扰，一般采用相对固定的几种典型航路，如跑道形和“8”字形。根据雷达干扰原理，雷达干扰无人机对雷达形成的干扰扇面随无人机运动而变化，对雷达形成的持久干扰扇面会小于瞬时干扰扇面。特别是无人机干扰距离较近，这一影响更加明显。一般情况下，指挥员希望持久干扰扇面尽量接近瞬时干扰扇面。本文拟通过提出“航路偏离代价”这一概念，对采用两种典型航路时无人机对雷达形成持久干扰扇面的大小进行对比，实现两种典型无人机压制干扰航路的优选。

1 两种典型的雷达干扰无人机压制干扰航路建模

在对雷达实施压制干扰时，为了保证良好的干扰效果，雷达干扰无人机往往在较小空间内对目标实施干扰。常见的干扰航路模式主要有两种:跑道形压制干扰航路和“8”字形压制干扰航路。

1.1 跑道形压制干扰航路模型

雷达干扰无人机跑道形压制干扰航路由两段半圆弧和两条平行直线航路构成，以雷达为坐标原点建立直角坐标系，如图1所示。

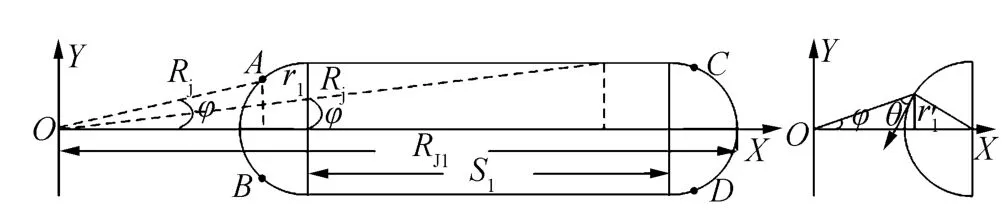
图1 雷达干扰无人机跑道形压制干扰航路示意图

基于图1，可将跑道形压制干扰航路的解析表达式描述为

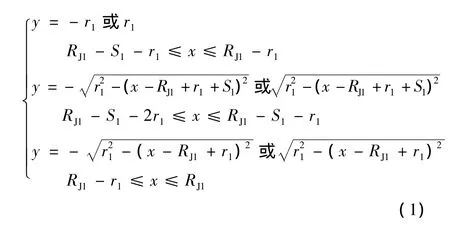
图1右图中r1'所示为:当无人机处在飞行航路雷达近端时，干扰波束离开雷达瞬间无人机离转弯中心距离在X轴上的投影。与之对应，当无人机处在飞行航路雷达远端时，干扰波束离开雷达瞬间无人机离转弯中心距离在X轴上的投影可用r1″表示。r1'、r1″如式(2)所示，其中，θfw为无人机干扰波束宽度。

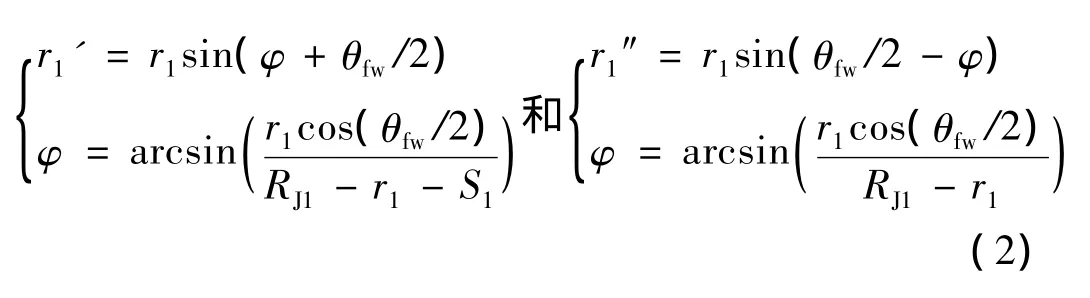
1.2 “8”字形压制干扰航路模型

雷达干扰无人机“8”字形压制干扰航路由两段半圆弧和两条相交直线航路构成，以雷达为坐标原点建立直角坐标系，如图2所示。

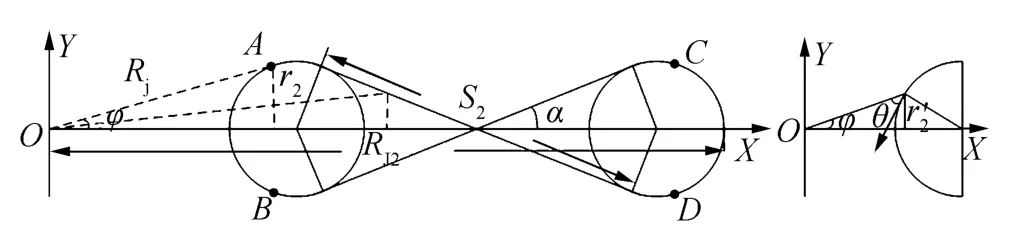
图2 实际天线方向图

基于图2，可将“8”字形压制干扰航路的解析表达式描述为

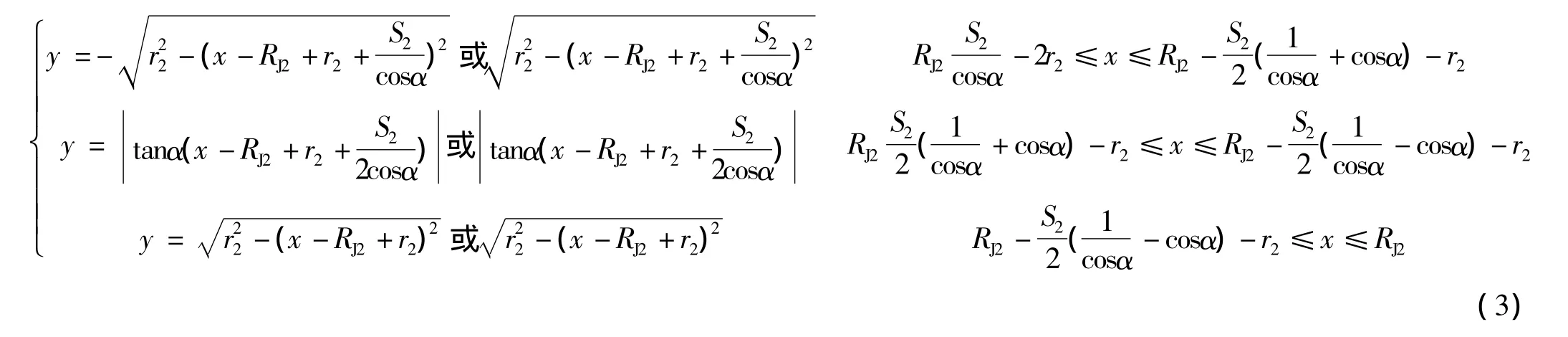
因雷达干扰无人机具有前向和后向干扰功能，所以存在4个干扰状态转换点，分别是A、B、C、D点。其中，A和B关于X轴对称，C和D也是关于X轴对称，无人机在弧AB和弧CD上不能对雷达实施干扰。

本文在同一区域对两种典型干扰航路进行研究，假设航路存在以下关系

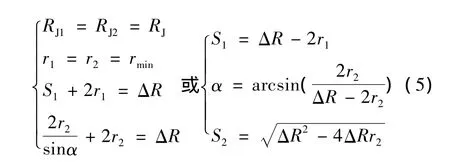
式中:RJ为航路远端与雷达之间距离;rmin为无人机最小转弯半径;ΔR为雷达干扰无人机航路纵向长度。

2 雷达干扰无人机压制干扰航路优选

2.1 航路偏离代价

航路偏离代价是航路上航程点和雷达连线，与中心轴(X轴)夹角的正切值，在整个航路上积分后取得的平均值。航路偏离代价描述的是航路整体偏离航路中心轴的程度。在干扰距离一定的情况下，两种航路对雷达形成的瞬时干扰扇面是相同的。航路偏离代价越大，航路整体偏离中心轴的程度越大，持久干扰扇面与瞬时干扰扇面之间差距越大，则持久干扰扇面越小，反之越大。

对于跑道形压制干扰航路而言，航路偏离代价求解的积分区间为［RJ1-S1-r1-r1'，RJ1-r1+r1″］。

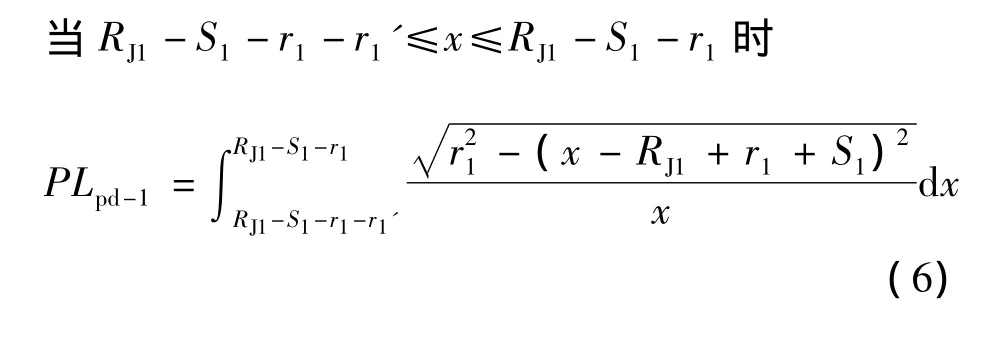
2.2 航路偏离代价与干扰距离关系

设 ΔR=10 km、rmin=1 km、θ=θfw/2=35°，得到航路偏离代价与干扰距离关系曲线，如图3所示。

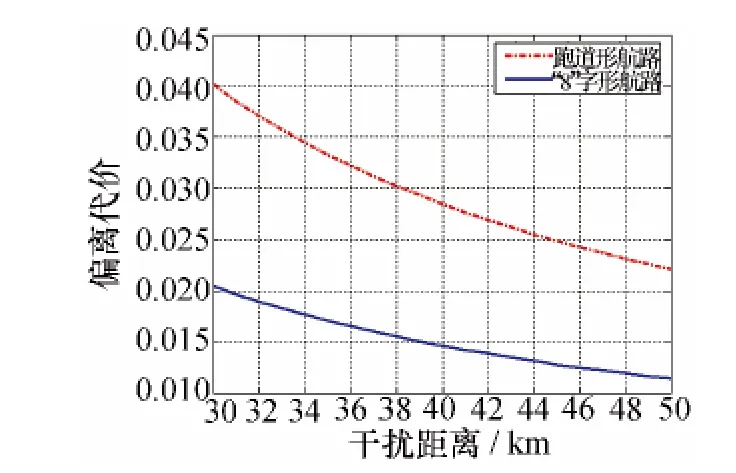
图3 航路偏离代价与干扰距离关系曲线

从图中可以看出，当航路纵向长度ΔR=10 km时，跑道形压制干扰航路与“8”字形压制干扰航路的航路偏离代价随着干扰距离的增大而减小，且“8”字形压制干扰航路的航路偏离代价始终小于跑道形压制干扰航路的偏离代价，说明采用“8”字形航路飞行的雷达干扰无人机对雷达形成的持久干扰扇面更大。

2.3 航路偏离代价与航路纵向长度关系

设 RJ=30 km、rmin=1 km、θ=θfw/2=35°，得到航路偏离代价与航路纵向长度关系曲线，如图4所示。

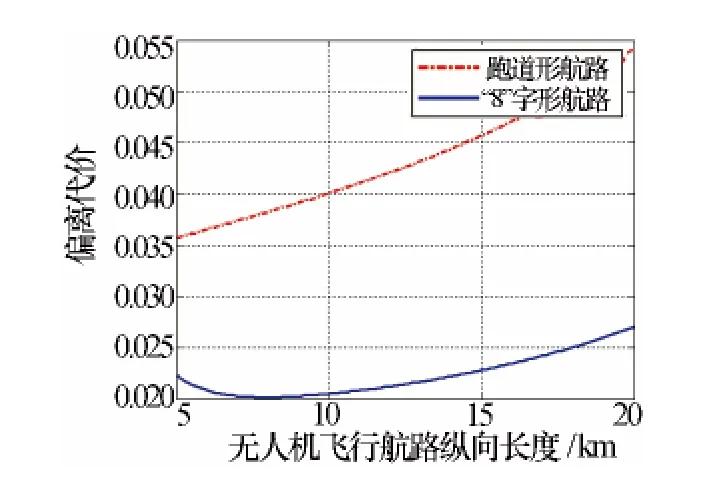
图4 航路偏离代价与航路纵向长度关系曲线

从图4中可以看出，在干扰距离RJ=30 km时，跑道形压制干扰航路偏离代价随着航路纵向长度的增加而增大;“8”字形压制干扰航路偏离代价随着航路纵向长度的增大先减小后增大，且“8”字形压制干扰航路的航路偏离代价始终小于跑道形航路，进一步说明，采用“8”字形航路飞行的雷达干扰无人机对雷达形成的持久干扰扇面更大。

“8”字形压制干扰航路偏离代价随着航路纵向长度的增大先减小后增大，“8”字形压制干扰航路偏离代价存在极小值。上述是在假设干扰距离固定的条件下得出的，当干扰距离变化，航路偏离代价最小值对应的航路纵向长度是否也发生变化?若航路偏离代价最小值对应的航路纵向长度随着干扰距离的变化而变化，那么变化趋势如何?

2.4 最佳航路纵向长度与干扰距离关系

为了解决上述一系列指挥员面临的问题，设干扰距离为 RJ∈［30 km，50 km］、rmin=1 km、θ=θfw/2=35°。经Matlab计算，航路偏离代价取得最小值时，对应的航路纵向长度与干扰距离之间关系，如图5所示。从图中可以看出，随着干扰距离的增大，最佳航路纵向长度随之增长。

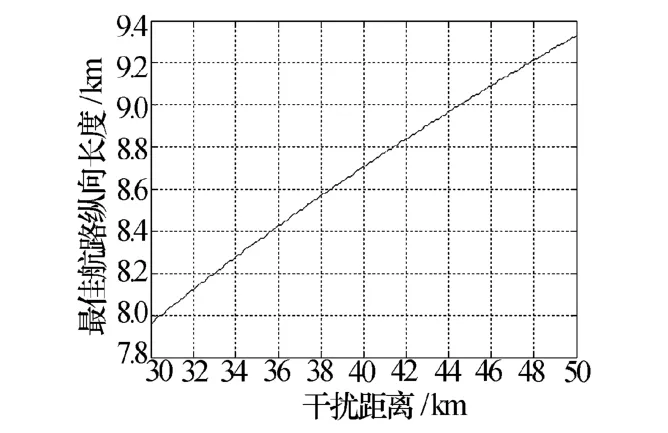
图5 最佳航路纵向长度与干扰距离之间的关系图

3 结束语

本文对两种典型雷达干扰无人机航路进行建模，利用“航路偏离代价”对二者进行评价。分析了航路偏离代价与干扰距离、航路纵向长度关系，比较得出:采用“8”字形航路飞行的雷达干扰无人机对雷达形成的持久干扰扇面大于采用跑道形航路飞行的雷达干扰无人机这一结论。在此基础上，计算得到了“8”字形压制干扰航路最佳航路纵向长度与干扰距离之间关系。

［1］ 王新益.无人机上的干扰载荷［J］.无人机，2006(3):55-58.Wang Xinyi.Interference load on the UAV［J］.Unmanned Vehicles，2006(3):55-58.

［2］杨 军，赵 峰，宫 颖.舰载无人机雷达对抗的建模研究［J］.系统仿真学报，2007，19(5):949-951.Yang Jun，Zhao Feng，Gong Ying.Research of shipborne UAV against radar［J］.Journal of System Simulation，2007，19(5):949-951.

［3］李大勇，叶琼龙.无人机在舰载电子对抗系统中的应用［J］. 电子对抗技术，2004，19(1):38-39.Li Dayong，Ye Qionglong.Application of the pilotless aircraft in naval EW system［J］.Technology of Electronic Countermeasure，2004，19(1):38-39.

［4］鞠 明，陈永光.空袭行动中雷达干扰无人机作战运用初探［J］.飞航导弹，2009(8):21-25.Ju Ming，Chen Yongguang.Research on operational application of radar jamming UAVs in air strikes［J］.Aerodynamic Missile Journal，2009(8):21-25.

［5］胡生亮，金嘉旺，许少云，等.电子战无人机在驱护编队反导作战中的使用研究［J］.舰船电子对抗，2005，28(3):3-5.Hu Shengliang，Jin Jiawang，Xu Shaoyun，el al.Research of EW UAV usage in destroyer&escort vessel formation［J］.Shipboard Electronic Countermeasure，2005，28(3):3-5.

［6］李修和，陈永光.假目标无人机系统的作战效能建模及模拟［J］.电子对抗技术，2004，19(3):32-35.Li Xiuhe，Chen Yongguang.Combat efficiency modeling and simulation of artificial object unmanned aerial vehicle system［J］.Technology of Electronic Countermeasure，2004，19(3):32-35.