基于ZMNL的相关广义复合分布雷达海杂波仿真

赵 翠，江朝抒，马 静，赵 越

(1.电子科技大学电子工程学院， 成都611731;2.航天系统仿真国防科技重点实验室， 北京100854)

0 引言

雷达海杂波建模与仿真技术一直备受关注，准确、快速地模拟海杂波，对雷达信号处理与海面目标检测具有重要的现实意义。国内外对实测的雷达海杂波数据做了大量的分析，传统的雷达杂波模型有瑞利分布、对数正态分布、Weibull分布、K分布［1-2］。瑞利分布能够较好地拟合低分辨率下的雷达海杂波的幅度分布。但在较高海情和较高的雷达分辨率的情况下，杂波的拖尾较长，对数正态分布与实测数据拟合得较好。Weibull分布的动态范围在对数正态分布和瑞利分布之间，在较宽的范围内表示实测海杂波的幅度分布更为精确。而K分布是由散斑分量和纹理分量两部分组成的复合模型，能够更准确地模拟海杂波。随着雷达带宽的增加，雷达杂波的散斑分量偏离高斯分布，调制分量偏离了伽马分布，因此K分布不再适用。

文献［2-4］首次提出了广义复合分布模型，文献［5］在此基础上提出了一种基于零记忆非线性变换(Zero Memory Nonlinear Transformation，ZMNL)方法的相关广义复合分布雷达杂波的仿真方法。本文分析了广义复合分布海杂波模型，并对文献［5］的方法进行了改进，提出一种相关广义复合分布雷达海杂波算法。这种算法采用独立产生杂波序列的幅度与相位的方法，可以避免求解复杂的非线性方程，具有运算量小的特点，且保证了滤波器的物理可实现性。最后，利用提出的算法仿真了几组相关广义复合分布海杂波序列，验证了此算法的准确性和可行性。

1 广义复合分布雷达海杂波模型

首先，介绍广义复合分布海杂波模型;然后，分析各个参数对其概率密度函数(Probability Density Function，PDF)的影响。

1.1 广义复合分布海杂波建模

雷达海杂波的复合模型可用式(1)来描述［6］

式中:X和Y分别是相互独立的短时间相关的快变分量(散斑分量)和长时间相关的慢变分量(纹理分量)。对于广义复合分布来说，X和Y是相互独立的广义伽马分布［3］，而X和Y可以由高斯随机分布序列通过非线性变换得到

当广义复合分布取特殊值时，就退化为其他常见的分布［2］。广义复合分布与其他常见分布的关系，如图1所示。

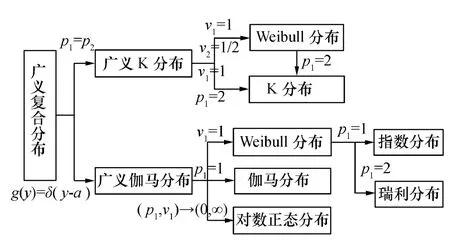
图1 广义复合分布与常见分布的关系

1.2 各个参数对广义复合分布PDF的影响

由式(4)可知:广义复合分布的PDF包含了五个参数 a、v1、v2，p1，p2。图 2 ～ 图 4 分别给出了 a、v1、p1取不同值时的广义复合分布的概率密度曲线的比较，v1与v2、p1与p2对广义复合分布的影响相同。每组数据的取值见图中注释。从图2中可以看出，参数a不影响分布的形状。从图3中可以看出，v1是偏斜度参数，影响分布形状的不对称性，其值越小，分布的不对称性越显著，倾斜度越大。由图4可以看出，功率参数p1影响分布的拖尾，其值越小，分布的拖尾越长。

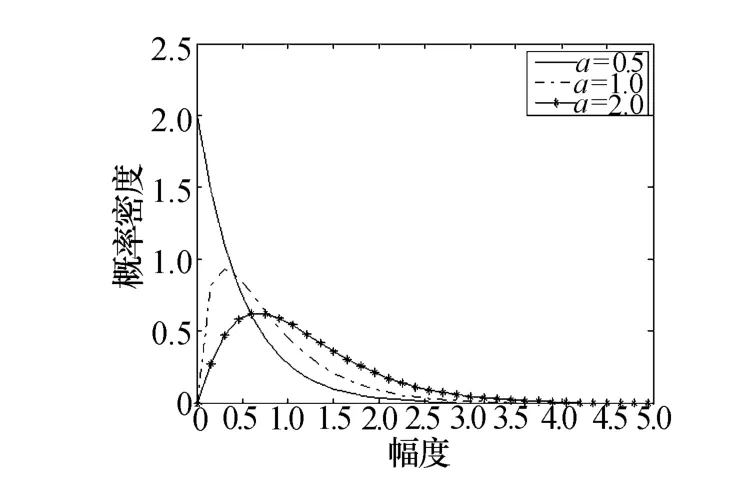
图2 参数a对广义复合分布的影响(v1=1，v2=1，p1=2，p2=2)

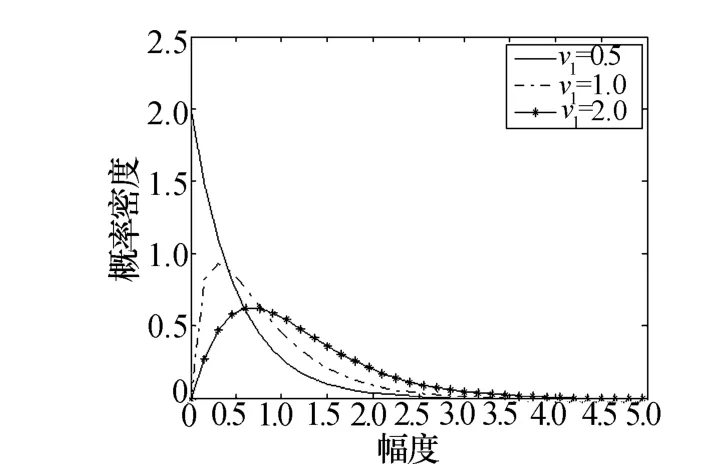
图3 参数v1对广义复合分布的影响(a=1，v2=1，p1=2，p2=2)

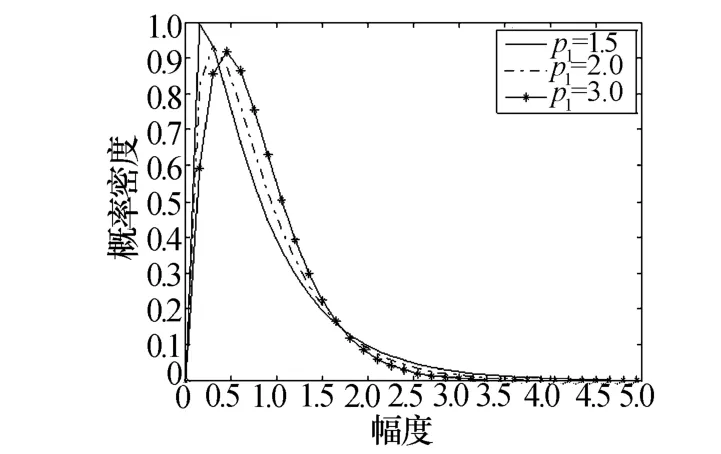
图4 参数p1对广义复合分布的影响(a=1，v1=1，v2=1，p2=2)

2 广义复合分布海杂波仿真

杂波仿真主要有两种方法:ZMNL和球不变随机过程(Spherically Invariant Random Process，SIRP)方法。本文在分析了广义复合分布与高斯分布序列之间关系的基础上，采用ZMNL方法来产生相关广义复合分布海杂波序列。实现相关广义复合分布海杂波的仿真的具体流程图，如图5所示。该方法的基本思想是:首先，得到广义复合分布随机序列;然后，加入相位信息 θ，其中 θ～U(0，2 π)，这样得到非相关(功率谱是白的)广义复合分布随机序列;最后，经过一个线性滤波器(决定了杂波的功率谱)得到相关广义复合分布随机序列。

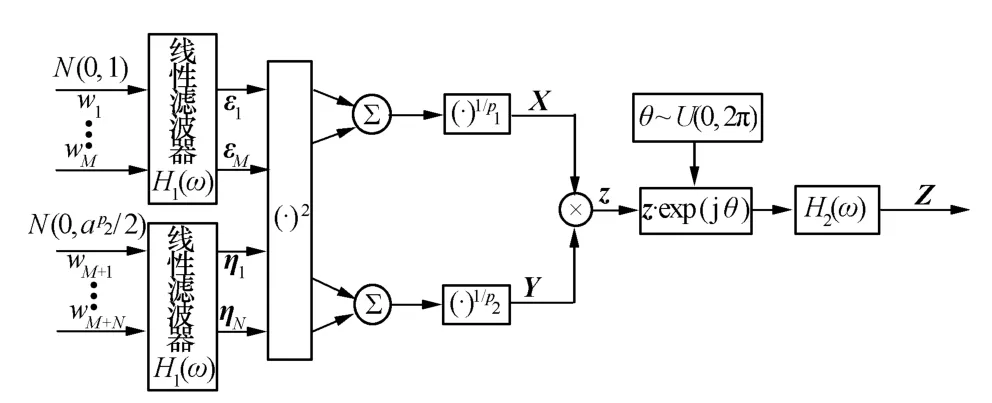
图5 相关广义复合分布仿真流程图

从图5可以看出，仿真过程主要分为两个部分:

(1)线性滤波器的设计。线性滤波器H1(ω)是窄带低通滤波器，把白高斯随机序列转换为相关高斯序列，是为了减小滤波器H2(ω)对z的幅度分布的影响。线性滤波器H2(ω)是由杂波的相关性(功率谱)决定的，主要有两个参数:滤波器的中心频率和带宽，而这两个参数与海杂波的功率谱有关。

(2)产生广义复合分布的随机序列。将独立的白高斯实随机序列经过线性滤波器H1(ω)变为窄带高斯随机序列，再经过非线性变换得到广义复合分布的随机序列。

从仿真过程来看，与文献［5］不同的是，该方法避免了求解复杂的非线性方程，而且用到的线性滤波器并没有忽略其相位特性，因此，滤波器是物理可实现。

3 仿真结果

在雷达杂波模拟中，线性滤波器H1(ω)的设计满足窄带宽的条件，减小后续滤波器H2(ω)对幅度的影响，就可以满足要求。仿真实验中，选择了带宽为0.1 π，阶数为50阶的FIR低通滤波器。

线性滤波器H2(ω)的参数主要有中心频率和带宽，这两个参数主要由海杂波频谱的中心频率和3 dB带宽确定，而海杂波的频谱由环境参数和雷达系统参数决定［7-8］。仿真试验中选择的中心频率为f0和3 dB，带宽f3dB分别为75 Hz和50 Hz，滤波器的阶数为50阶。

本文利用第2节中提出的方法产生了五组相关广义复合分布的海杂波序列，数据长度为8 000，雷达的脉冲重复频率为1 000 Hz，其中，仿真的功率谱是由周期图方法估计得到的。具体的仿真参数如表1所示。图6a)、图7a)、图8a)、图9a)、图 10a)分别是相关广义复合分布海杂波序列的统计直方图与理论概率密度曲线的比较，图6b)、图7b)、图8b)、图9b)、图10b)是相关广义复合分布海杂波序列的功率谱曲线与理论功率谱曲线的比较。图6～图8分别是广义复合分布退化为Weibull分布、K分布和广义K分布的情况下的仿真结果，图9、图10是普通广义复合分布的仿真结果。由仿真图可以看出，使用提出的方法模拟的相关广义复合分布海杂波序列，幅度统计特性和功率谱特性与理论值拟合的比较好。

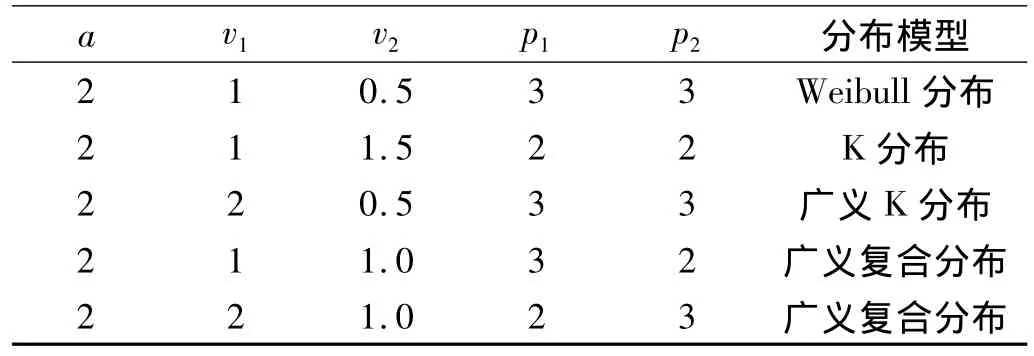
表1 幅度分布的仿真参数

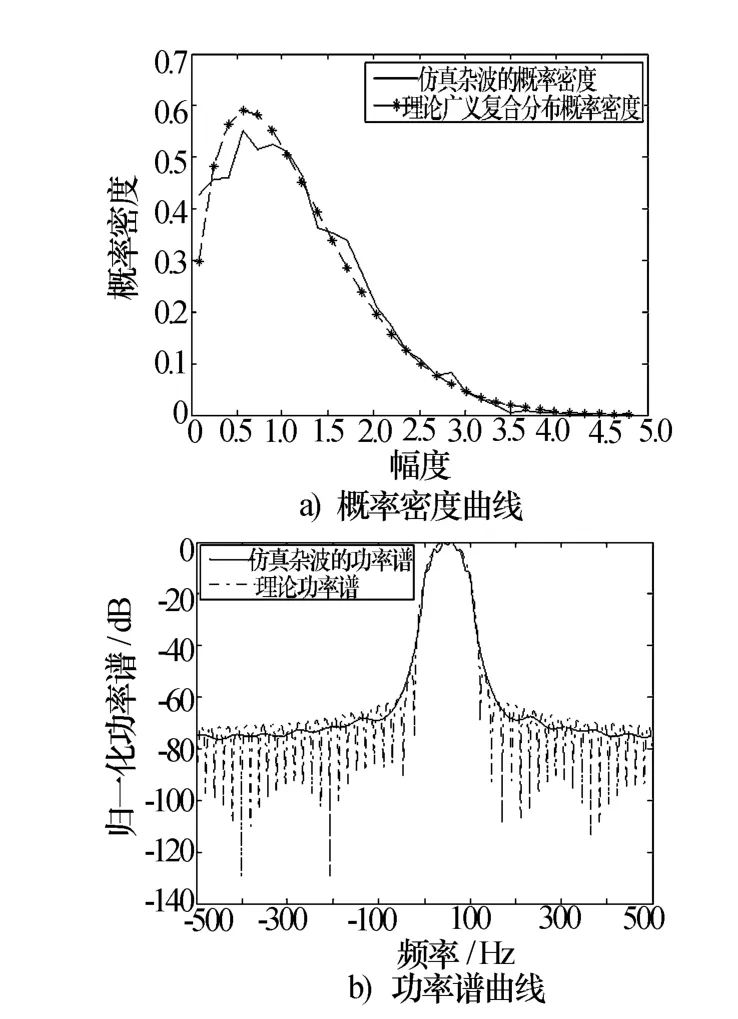
图6 Weibull分布

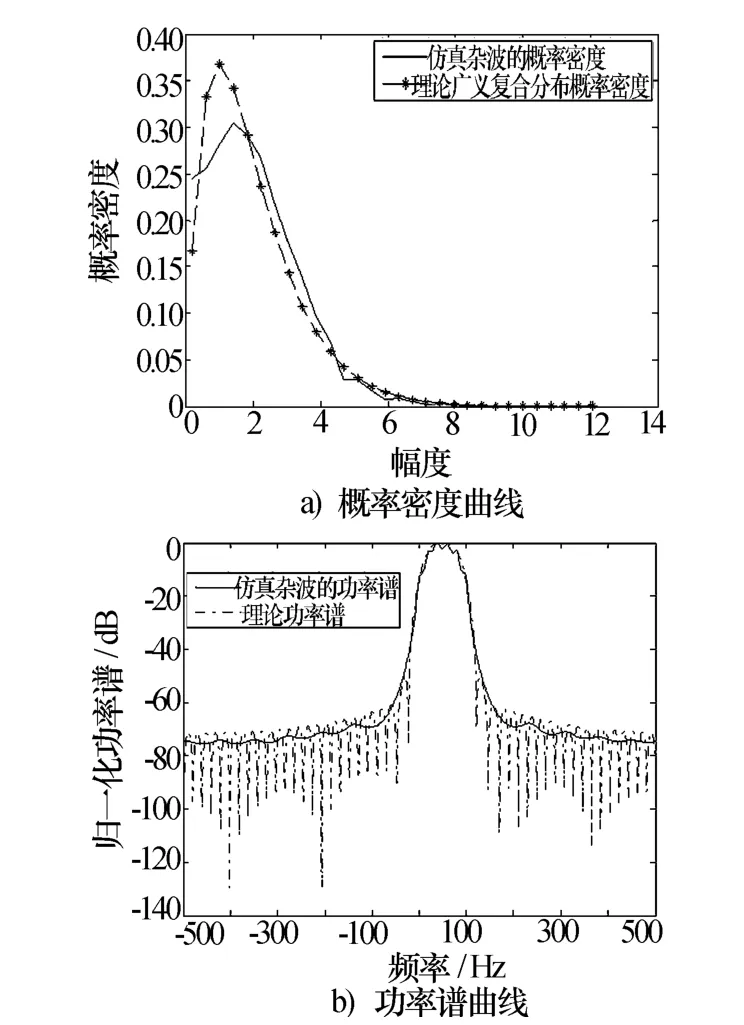
图7 K分布

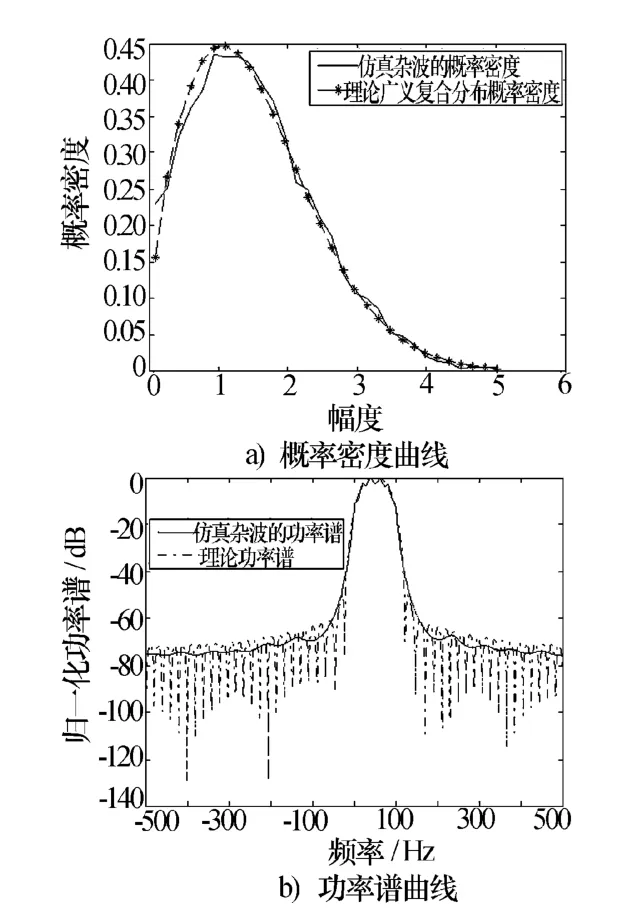
图8 广义K分布

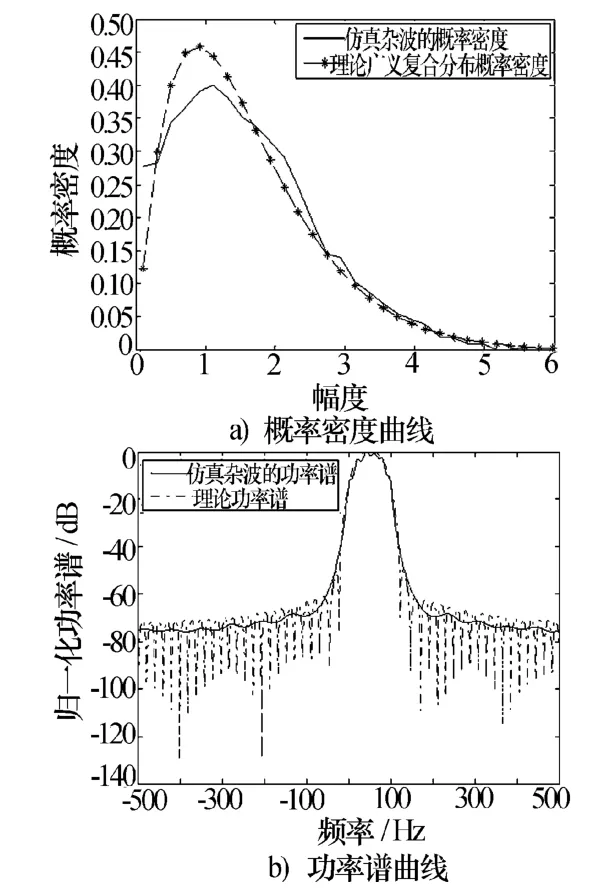
图9 一般广义复合分布

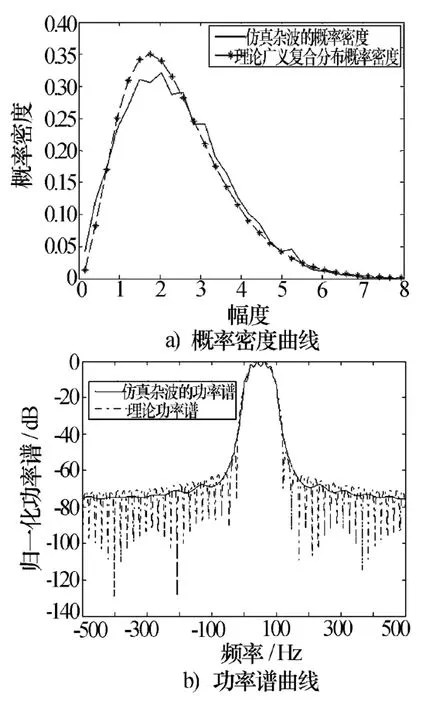
图10 一般广义复合分布

4 结束语

由于传统的瑞利分布、Weibull分布、K分布、对数正态分布等都是广义复合分布的特例，广义复合分布更具有普遍性，为雷达海杂波建模与仿真带来了一定的方便。本文分析了广义复合分布海杂波模型，并提出了一种ZMNL方法，对相关广义复合分布海杂波进行了模拟，这种方法由于不需要求解非线性方程，因此，运算量小且滤波器也是物理可实现的。后续的仿真结果也证明了这种方法的有效性。但是，由于参数M、N是由参数v1、v2决定的整数，因此，这种仿真方法只能仿真参数v1、v2为整数或者半整数的广义复合分布海杂波，这是未来需要解决的问题。

［1］Carretero J，Blanco A.Statistical analysis of a high resolution sea clutter database［J］.IEEE Transaction on Geoscience and Remote Sensing，2010，48(4):2024-2037.

［2］Anastassopoulos V，Lampropoulos G A.A generalized compound model for radar clutter［C］//Proceedings of the IEEE National Radar Conference.Toronto，Canada:IEEE Press，1994:41-45.

［3］Anastassopoulos V，Lampropoulos G A.High resolution radar clutter classification［C］//Proceedings of the IEEE International RadarConference.Toronto，Canada:IEEE Press，1995:662-667.

［4］Anastassopoulos V，Lampropoulos G A.High resolution radar clutter statistic［J］.IEEE Transactions on Aerospace and Electronic System，1999，35(1):43-59.

［5］谢灵巧，陈祝明，江朝抒，等.基于ZMNL的相关广义复合分布宽带雷达杂波仿真［J］.信号处理，2009，25(9):1463-1468.Xie Lingqiao，Chen Zhuming，Jiang Chaoshu，et al.Simulation of the correlated generalized compound distribution wide band radar clutter using ZMNL method［J］.Signal Processing，2009，25(9):1463-1468.

［6］Ward K D.Compound representation of high resolution sea clutter［J］.Electronics letters，1981，17(16):561-563.

［7］Skolnik M I.雷达手册［M］.3版.北京:电子工业出版社，2010.Skolnik M I.Radar handbook［M］.3rd ed.Beijing:Publishing House of Electronics Industry，2010.

［8］赵巨波，符 燕，耿文东，等.海杂波统计特性分析［J］.现代雷达.2005，27(11):4-6.Zhao Jubo，Fu Yan，Geng Wendong，et al.Analysis of sea clutter statistical characteristics［J］.Modern Radar，2005，27(11):4-6.