具有时滞和不同潜伏阶段的艾滋病模型的Hopf分支

尹锦锦，胡志兴

（北京科技大学 数理学院，北京 100083）

艾滋病（Acquired Immune Deficiency Syndrome，AIDS），即获得性免疫缺陷综合征，是人类因为感染免疫缺陷病毒（Human Immunodeficiency Virus，HIV）后导致的免疫缺陷，并发一系列机会性感染及肿瘤，严重者可导致死亡.1981年，人类免疫缺陷病毒首次在美国发现.HIV是一种能攻击人体免疫系统的病毒，有很长的潜伏期和传染期.由于较长的传染期，一般会经过几个感染阶段最终发展为成熟的艾滋病［1］.

时滞在一些传染病模型［2－5］中被许多研究者考虑.由于各种实际原因，如免疫和治疗，时滞可能会出现在流行病研究中.对于某些疾病（如流感、结核、艾滋病、麻疹等），易感者暴露后容易被接触感染，也就是说，被感染的个体可能不具有传染性，此感染者仍然经过一定的潜伏期才成为传染性易感者.文献［4］建立了一个带有时滞和脉冲接种的传染病模型，文献［5］提出一个具有明确潜伏期和离散时滞微分方程的AIDS模型.本文引入时滞，建立一个带有时滞和不同潜伏阶段的AIDS模型，根据参数值研究时滞对疾病平衡点稳定性的影响.

1 模型的建立

艾滋病模型考虑将总人口分为5个仓室，分别为易感染类S、慢潜伏类I1、快潜伏类I2、出现症状阶段J和完全获得AIDS为A.文献［6］建立了如下模型:

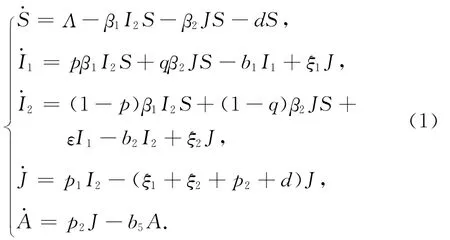
其中:Λ表示人口的输入率，β1表示快潜伏类的转移系数，β2表示有症状阶段的转移系数，p表示S被I2感染后进入I1的部分，q是S被J感染后进入I1的部分，ε是I1到I2的进入率，p1是I2到J的进入率，p2是J到A的进入率，ξ1是从J到I1的治疗率，ξ2是从J到I2的治疗率，d是自然死亡率，b1＝ε＋d，b2＝p1＋d，b5＝α＋d.α是与疾病有关的死亡率.

由于模型（1）中变量A在前4个式中没有出现，只考虑系统（1）的前4个方程构成的子系统.本文对模型（1）的前4个方程构成的子系统引入时滞，研究时滞对疾病平衡点的影响.设τ为表示出现症状的J经过治疗转变为无症状的I2，且直到I2的治疗效果可见时的时间，其模型如下:

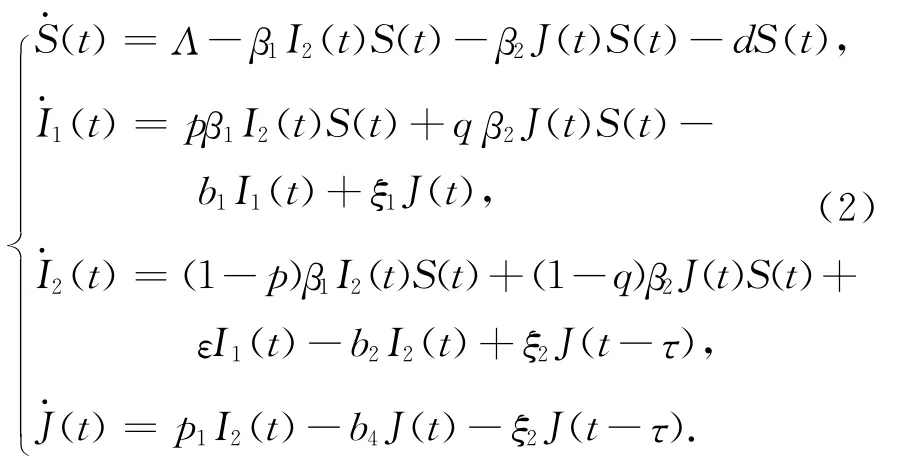
其中b4＝ξ1＋p2＋d，其他变量代表的意义同模型（1）.

定义模型的基本再生数

模型（2）的初始条件为

其中φi（θ）≥0，θ∈ ［－τ，0］，φi（0）＞0（i＝1，2，3，4），且 （φ1（θ），φ2（θ），φ3（θ），φ4（θ））∈C（［－τ，0］，）.记X＝C（［－τ，0］，）是从区间［－τ，0］映射到的连续函数的Banach空间，并且此空间具有拓扑一致收敛性，＝ ｛（x1，x2，x3，x4）｜xi≥0，i＝1，2，3，4｝.

2 平衡点的存在性和无病平衡点的稳定性分析

模型（2）总是有无病平衡点E（，0，0，0）；如0果R0＞1，那么模型（2）有疾病平衡点E＊（S＊，，，J＊），这里

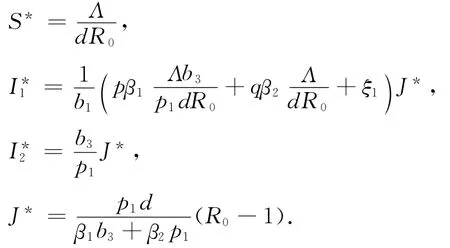
系统（2）在无病平衡点E0的特征方程为

这里P（λ）＝λ3＋d1λ2＋d2λ＋d3，Q（λ）＝e1λ2＋e2λ＋e3，其中

特征方程（3）有一个特征根λ＝－d＜0，其他的特征根由P（λ）＋Q（λ）e－λτ＝0决定.设

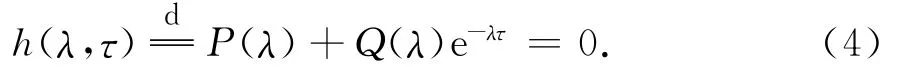
当τ＝0时，由文献［6］中定理2知无病平衡点E0是全局渐近稳定的.

当R0＜1和τ＞0时，λ＝iω（ω＞0）为方程（4）的纯虚根，则将λ＝iω（ω＞0）带入方程（4），分离实部和虚部，消去三角函数得

其中y＝ω2，γ1＝－2d2－，γ2＝2e1e3－2d1d3＋－，γ3＝－.

不难证明:当－3γ2＜0和γ3≥0时方程（5）没有正实根，也就是不存在正数ω使得iω是方程（3）的特征根.由Rouche′s定理可知，对所有的τ≥0特征方程（3）的所有特征根都有负实部.

当τ＝0时，如果R0＞1，设h（λ）＝λ3＋（d1＋e1）λ2＋（d2＋e2）λ＋（d3＋e3），则

引理1 若R0＜1，－3γ2＜0和γ3≥0，则系统（2）的无病平衡点E0是局部渐近稳定的；若R0＞1，则无病平衡点E0是不稳定的.

3 疾病平衡点和Hopf分支

以下讨论时滞对疾病平衡点稳定性的影响.模型（2）在平衡点E＊（S＊，I，，J＊）处的特征方程为

其中f（λ）＝λ4＋m1λ3＋m2λ2＋m3λ＋m4，

当τ＝0时方程（6）为f（λ）＋g（λ）＝0，即

其中a1＝m1＋n1，a2＝m2＋n2，a3＝m3＋n3，a4＝m4＋n4.根据Hurwitz判别条件，若ai＞0（i＝1，2，3，4）和a3（a1a1－a3）－4＞0，则特征方程（7）有负实部的根.

引理2 当τ＝0时，若ai＞0（i＝1，2，3，4）和a3（a1a2－a3）－4＞0，则模型（2）的疾病平衡点E＊是局部渐近稳定的.

根据文献［7］定理9.17.4和τ的连续性，特征方程（6）有正实部的根当且仅当它有纯虚根.如果方程（6）有纯虚根，这样就能够找到条件使方程（6）的所有特征根有负实部.

设λ＝α（τ）＋iω（τ）（ω＞0）为方程（6）的根，这里α（τ）和ω（τ）依赖于时滞τ.当τ＝0时，模型（2）的疾病平衡点E＊是稳定的.根据连续性，对于充分小的τ＞0仍有α（τ）＜0和E＊稳定.因为对于特定的τ0＞0有α（τ0）＝0，这样就有λ＝iω（τ0）是方程（6）的纯虚根，从而疾病平衡点E＊就可能失去稳定性，最终当α（τ）增加到正的时E＊就变得不稳定.换言之，若这样的ω（τ0）不存在，则方程（6）对所有时滞τ都没有纯虚根，从而正平衡点E＊对所有τ＞0都是稳定的.

当R0＞1和τ＞0时，假设方程（6）有根λ＝iω且ω＞0，将λ＝iω带入（6），分离实部和虚部，消去三角函数得

这里x＝ω2，α1＝m1－2m2－，

因而，若特征方程（6）有一纯虚根λ＝iω，则方程（8）有一正实根ω2.假设方程（8）有（1≤≤4）个正实根，分别记为xn（1≤n≤），设Qn＝（－m2xn＋m4）（n2xn－n4）＋xn（－m1xn＋m3）（n1xn－n3），

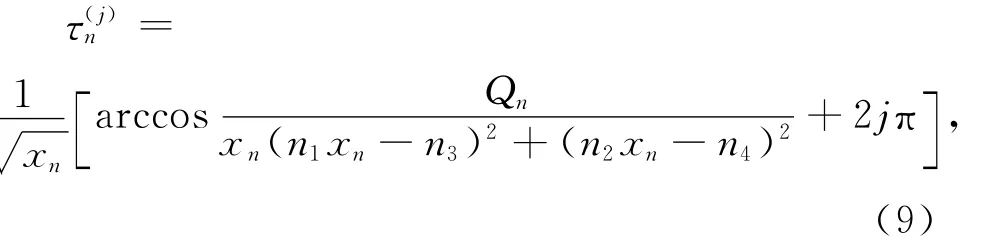
这里1≤n≤，j＝0，1，2，….这样就证明了特征方程（6）有一对纯虚根±i.对每一个整数j和1≤n≤，设为特征方程（6）在附近的根并且满足

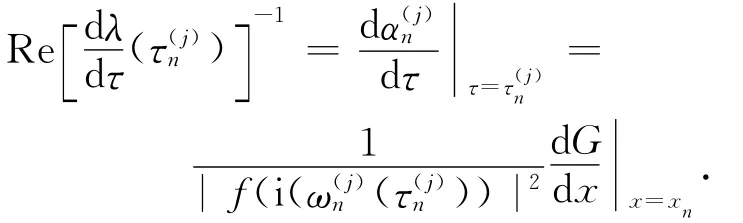
即得定理1的结论.

应用定理1和Hopf分支定理［8］，能够得到下面的Hopf分支存在定理.

定理2 （1）若方程（8）没有正实根，则对任意τ＞0，正平衡点E＊是局部渐近稳定的；（2）若方程（8）有正实根，那么对τ∈［0，］，正平衡点E＊是局部渐近稳定的，这里j＝0，1，2，…｝，τ（j）n如公式（9）定义；（3）更进一步有，如果xn0是方程（8）的单根，则系统（2）在τ＝处产生Hopf分支.

4 分支周期解的稳定性分析

用文献［8］的方法来分析分支周期解的稳定性.假设

（H1）当τ＝τ0时方程（7）有一对纯虚根±iω0，这里τ0∈｜1≤n≤，j＝0，1，2，…｝；

（H2）是方程（8）的单根，即G′（）≠0；

（H3）方程（6）的其他根有严格的负实部.

若用μ＝τ－τ0作为一个新的分支变量，则μ＝0就是Hopf分支的值.设

因此系统（2）可以写为

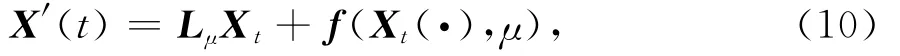
这里Lμφ＝F1φ（0）＋F2φ（－τ），

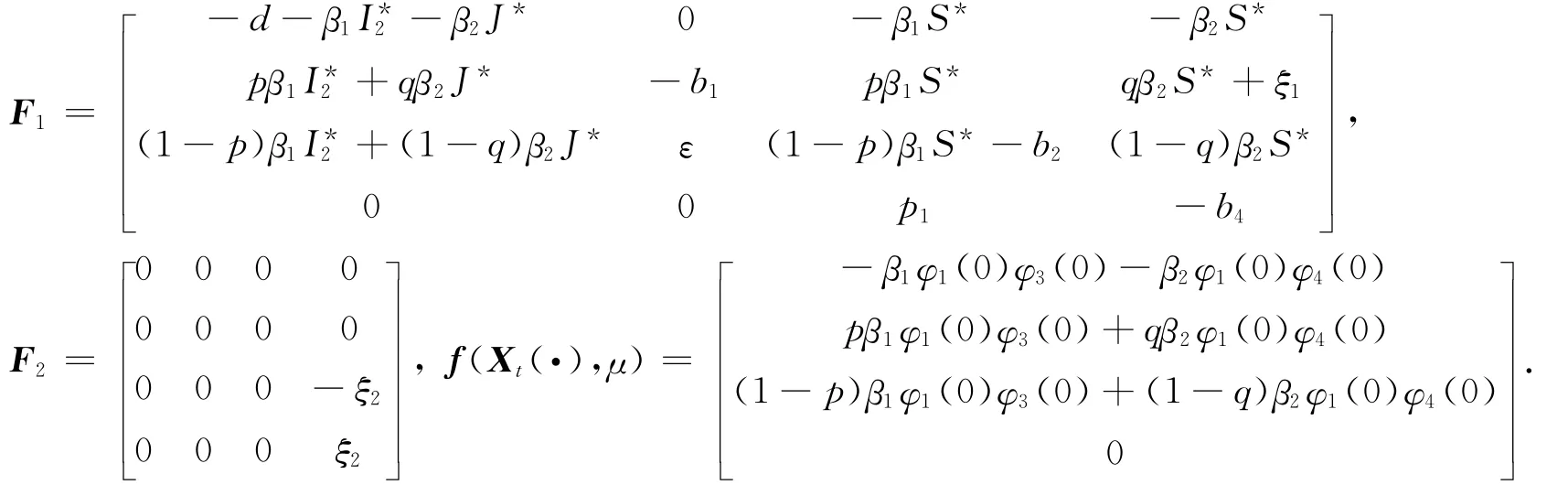
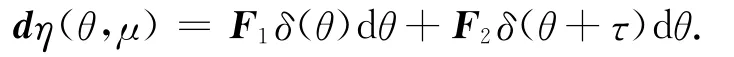
定义

这里φ∈C（［－τ，0］，R4）.

因此（10）变为

对ψ∈C（［－τ，0］，R4），A＊（0）是A（0）的共轭算子，定义A＊（0）如下:

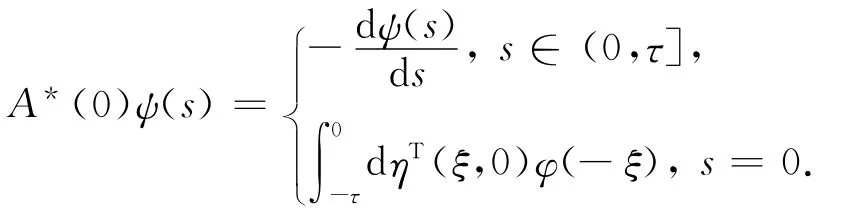
把A（0）、A＊（0）、η（θ，0）和R（0）分别简写为A、A＊、η（θ）和R.对φ∈C（［－τ，0］，R4）和ψ∈C（［－τ，0］，R4）定义内积:

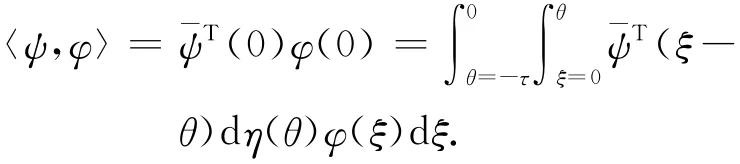
定义h（θ）和h＊（s）为A和A＊对应于特征值iω0和－iω0的特征向量，则有

下面选择h（θ）和h＊（s）满足〈h，h＊〉＝1.h（θ）＝ （1，h2，h3，h4）Teiω0θ和h＊（s） ＝D（1，，，）Teiω0s.这里

根据文献［8］的方法，得到下面的系数:

计算出g20、g11、g02和g21，这样就能得到下面的变量值:

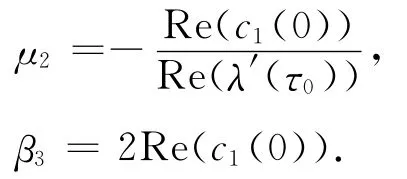
其中μ2的符号决定Hopf分支的方向:若μ2＞0，则分支周期解在μ＞0（τ＞τ0）时存在；β3的符号决定分支周期解的稳定性:当β3＜0时周期解是稳定的.由于sign［Reλ′（τ0）］＝sign［G′（ω0）］.

设＝－，则得到

定理3 假设（H1）、（H2）、（H3）成立，（1）若＞0＜0），则当τ＞τ0（τ＜τ0）时分支周期解是存在的；（2）若β3＜0，则当t→＋∞时分支周期解是轨道渐近稳定的.

容易证明当τ0＝时，这里由（10）式定义，由定理2的条件（2）的证明知道:分支周期解的存在性和稳定性仅由 Re（c1（0））决定.特别地，若Re（c1（0））＜0，由定理3可知:当τ＞τ0时存在稳定的周期解.

5 数值模拟

以下用数值模拟来证明周期解的稳定性理论.选取参数:Λ＝4.343 6，β1＝1.585 3，β2＝2.044 9，d＝0.549 0，p1＝2.429 9，p2＝0.200 1，ε＝3.325 0，ξ1＝0.924 1，ξ2＝4.957 2，p＝0.633 6，q＝0.701 7，则R0＝19.226 2＞1，平衡点E＊（0.411 5，1.071 4，4.285 8，1.570 7），方程（10）有一个正实根，满足定理1中的条件（2），计算得τ0＝1.098 3.应用定理2，当τ＜τ0时E＊是稳定的，其相图如图1所示.经计算得c1（0）＝－0.449 5＋0.112 2i，则当τ＞τ0时存在稳定的周期解，其相图如图2所示.

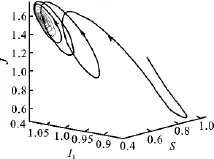
图1 当τ＝0.6＜τ0时E＊是稳定的Fig.1 E＊is stable forτ＝0.6＜τ0

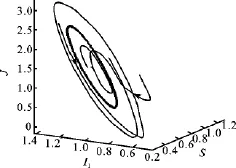
图2 当τ＝1.1＞τ0时有一个稳定的周期解Fig.2 A stable periodic solution forτ＝1.1＞τ0

6 结语

本文研究具有时滞和两种潜伏期的AIDS模型，讨论了模型的动力学行为.得到基本再生数R0.对比文献［6］中的研究，我们引入的时滞改变了疾病平衡点E＊的稳定性，得到疾病平衡点E＊在τ∈［0，τ0）时是局部渐近稳定的，随着τ的增大E＊开始变得不稳定最终出现分支周期解.用文献［8］中的方法证明了分支周期解的稳定性，并且由定理2知道周期解的稳定性仅由Re（c1（0））决定.数值模拟验证了结论的正确性.

［1］Levy J A.Pathogenesis of human immunodeficiency virus infection［J］.Microbiological Reviews，1993，57:183-289.

［2］Wang Wendi，Ma Zhien.Global dynamics of an epidemic model with time delay［J］.Nonlinear Analysis Real World Applications，2002，3（3）:365-373.

［3］Gao Shujing，Chen Lansun，Nieto J，et al.Analysis of a delayed epidemic model with pulse vaccination and saturation incidence［J］.Lancet，2006，24（35/36）:6037-6045.

［4］Mukandavire Z，Garira W，Chiyaka C.Asymptotic properties of an HIV/AIDS model with a time delay［J］.Journal of Mathematical Analysis and Applications，2007，330（2）:916-933.

［5］Watmough J，Vanden Driessche P.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission［J］.Mathematical Biosciences，2002，180:29-48.

［6］Huo Haifeng，Feng Lixiang.Global stability for an HIV/AIDS epidemic model with different latent stages and treatment［J］.Journal of Mathematical Analysis and Applications，2013，37:1480-1489.

［7］Dieudonne J.Foundations of modern analysis［M］.New York:Academic Press，1960:243.

［8］Hassard B D，Kazarinoff N D，Wan Y H.Theory and applications of Hopf bifurcation［M］.Cambridge:Cambridge University Press，1981:14-144.