几类效应代数的张量积及其可表示性

孟会贤，曹怀信

（陕西师范大学 数学与信息科学学院，陕西 西安 710119）

效应代数是产生于量子信息理论的一类重要代数结构.在量子力学中，量子系统用一个复的Hilbert空间H描述，系统的可观测量用H上的正压缩算子表示，量子效应的全体是C＊-代数B（H）中的一个闭凸集:

它具有部分二元运算A⊕BA＋B且每一个量子效应T都有唯一的补元T′满足T⊕T′＝I，称ε（H）为 Hilbert空间效应代数［1－10］.抽象效应代数概念是由Foulis和Bennett在文献［1］中提出的，其目的是表示不可精确测量的量子逻辑结构.它不仅包括Hilbert空间效应代数，还包括正交模格、Boolean代数、模糊集系统等代数结构.抽象效应代数不一定形如ε（H）.为了研究效应代数的分类问题，文献［11］引入并讨论了效应代数的表示问题.文献［12］进一步研究了效应代数表示与弱表示问题.在文献［13］中，我们利用态空间的性质，建立了可表示效应代数的刻画定理，由此给出可表示效应代数的一些运算性质.特别研究了效应代数的张量积的表示问题.基于态空间在研究效应代数表示问题中的重要性，文献［14］讨论了效应代数上态的存在性，给出一些效应代数的态空间.文献［15］利用D-test空间，证明了两个效应代数E1与E2的张量积存在的充分必要条件是存在一个效应代数F及双态射σ:E1×E2→F；同时，还指出两个效应代数的张量积在同构意义下是唯一的.

由于效应代数张量积的定义是“存在性的”且使用了“范畴”的思想，并不是“构造性”，所以构造具体效应代数的张量积显得十分困难.本文将给出几个重要效应代数的张量积的构造，并讨论它们的可表示性.

1 基本概念

定义1 设E为非空集合，0与1是E中两个不同的元素，⊕是E上的一个部分二元运算，满足下列条件:

（E1）交换律:当a、b∈E且a⊕b有定义（记作a⊥b）时，b⊥a且a⊕b＝b⊕a；

（E2）结合律:当a、b、c∈E，a⊕b且（a⊕b）⊥c时，b⊥c、a⊥（b⊕c）且（a⊕b）⊕c＝a⊕（b⊕c）；

（E3）正交补:对于任意的a∈E，都存在唯一的b∈E使得a⊕b＝1（b称为a的正交补，记作a′）；

（E4）0-1律:当a∈E且a⊥1时，有a＝0，则称（E，⊕，0，1）为一个效应代数，简称E为一个效应代数.

显然（［0，1］，＋，0，1）为效应代数.

定义2 设E与F为两个效应代数，如果映射φ:E→F满足:a、b∈E，a⊥b⇒φ（a）⊥φ（b）且φ（a⊕b）＝φ（a）⊕φ（b）成立，那么称φ:E→F是可加的.若φ:E→F为一个可加映射，且满足φ（1）＝1，则称φ:E→F为态射.特别地，若φ:E→［0，1］为态射，则称φ为E上的态，E上所有态的集合记作S（E）.若φ:E→F为态射且当a、b∈E，φ（a）⊥φ（b）时，有a⊥b成立，则称φ:E→F为单调态射.一个满的单调态射φ:E→F称为从E到F上的同构.如果存在同构φ:E→F，则称E和F是同构的.

定义3［11］设E为效应代数，若存在 Hilbert空间H和单调态射φ:E→ε（H），则称E是可表示的，且称（φ，H）是E的一个表示；否则，称E是不可表示的.

定理1［13］设E为效应代数，S（E）≠Ø，则下列论述等价:

（1）E是可表示的；

（2）x、y∈E，f（x）＋f（y）≤1（∀f∈S（E））⇒x⊥y.

定义4［15］设E1、E2、E均为效应代数，若映射σ:E1×E2→E满足下列条件:

（1）σ（1，1）＝1；

（2）∀x∈E1，σ（x，·）:E2→E是可加的；

（3）∀y∈E2，σ（·，y）:E1→E是可加的，则称σ为双态射.

由定义可知:

推论1 设映射σ:E1×E2→E为双态射，则

（1）当x∈E1、n∈N且nx有定义（即n个x是可加的）时，对于任意y∈E2，nσ（x，y）也有定义，且σ（nx，y）＝nσ（x，y）；

（2）当y∈E2、m∈N且my有定义时，对于任意x∈E1，mσ（x，y）也有定义，且σ（x，my）＝mσ（x，y）.

定义5［15］若存在双态射σ:E1×E2→E使得

（1）对于任意的效应代数F及双态射β:E1×E2→F，都存在态射φ:E→F使得φ◦σ＝β；

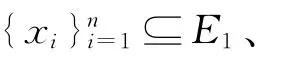
考虑到范畴角度研究效应代数的张量积的抽象性，我们构造出几类效应代数的张量积，并讨论它们的可表示性.

2 主要结果

命题1 若效应代数E＝E1⊗σE2，效应代数F＝E1⊗τE2，则E与F是同构的.

所以φ◦φ＝I｜E.同理，φ◦φ＝I｜F.故态射为φ的逆映射为态射φ，因此φ:E→F为效应代数同构，从而效应代数E与效应代数F是同构的.

命题2 设（E，0，1，⊕）为效应代数，若定义映射σ:｛0，1｝×E→E为σ（x，y）＝0，其中x＝0或y＝0；σ（1，a）＝a，∀a∈E，则E＝｛0，1｝⊕σE.

证明 显然，σ（1，1）＝1，σ（0，·）:E→E是可加的，且∀x∈E，σ（·，x）:｛0，1｝→E是可加的.设x、y∈E，x⊥y，由σ定义知σ（1，x）⊥σ（1，y）且σ（1，x⊕y）＝σ（1，x）⊕σ（1，y），因此σ（1，·）:E→E是可加的，所以σ是双态射.设L为任意效应代数，β:｛0，1｝×E→L为双态射，令φ:E→L为φ＝β（1，·），则φ为态射，又由σ、φ的定义知φ◦σ＝β，故定义5的条件（1）满足.显然，定义5的条件（2）满足，所以E＝｛0，1｝⊗σE.证毕.

对任意m∈N＋，记

其中0a＝0，ma＝1.当r＋s≤m时，定义ra⊕sa＝（r＋s）a，则（Cm（a），⊕，0，1）为可表示的效应代数［文献10，例2.8］.下面构造效应代数Cm（a）与Cn（a）的张量积，并讨论它的可表示性.

命题3 设映射σ:Cm（a）×Cn（b）→Cmn（c）为σ（ra，sb）＝rsc，则σ为双态射，且Cm（a）⊗σCn（b）＝Cmn（c）.

证明 容易验证:σ为双态射.先证明定义5的条件（1）满足.对于任意的效应代数L及双态射β:Cm（a）×Cn（b）→L，定义φ:Cmn（c）→L为φ（tc）＝tβ（a，b）（∀t∈Δmn），则φ为 态射，且 ∀r∈Δm，s∈Δn有

由此可见φ◦σ＝β.对任意的t∈Δmn，记t＝ms＋r，其中r＝0，1，…，m－1；s＝0，1，…，n；则

从而，定义5的条件（2）满足.故Cmn（c）为效应代数Cm（a）与Cn（b）关于σ的张量积，即Cm（a）⊗σCn（b）＝Cmn（c）.证毕.

在集合C′4（y，z）＝｛0，y，z，1｝上定义运算⊕，定义:y⊕z＝z⊕y＝1，u⊕0＝0⊕u＝u（u＝0，y，z，1），则（C′4（y，z），⊕，0，1）为效应代数.由文献［12］知:C′4（y，z）是可表示的效应代数.

下面构造效应代数C2（x）与C′4（y，z）的张量积，并讨论它的可表示性.

命题4 设E＝｛0，a，b，c，d，e，f，1｝，在集合E上定义运算⊕如下:

⊕0 a b c d e f g 1 0 0 a b c d e f g 1 a a d f b g 1 b b f 1 g c c b g e f 1 d d f 1 e e g 1 f f 1 g g 1 1 1

则

（1）（E，0，1，⊕）是可表示的效应代数，其态空间为S（E）＝｛φλ:λ∈［0，0.5］｝，其中

（2）C2（x）⊗σC′4（y，z）＝E，其中映射σ:C2（x）×C′4（y，z）→E为

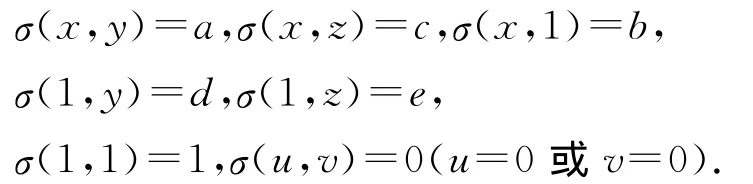
证明 （1）容易检验:E是效应代数.对任意λ∈［0，0.5］，容易验证φλ为E上的态射.设φ∈S（E），φ（a）＝λ，由b⊕b＝1知1＝φ（1）＝φ（b⊕b）＝φ（b）＋φ（b），因此φ（b）＝0.5.类似可知

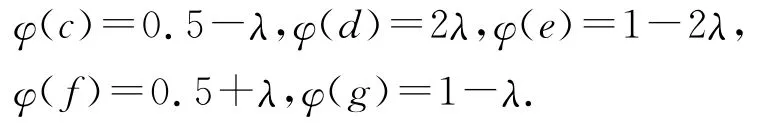
故λ∈［0，0.5］且φ＝φλ，所以S（E）＝｛φλ:λ∈［0，0.5］｝.可以验证:当p、q∈E不可加时，必有E的态φλ使得φλ（p）＋φλ（q）＞1.从而，定理1中条件（2）成立，所以（E，0，1，⊕）是可表示的效应代数.

（2）容易验证:σ为双态射.设L为任意效应代数，β:C2（x）×（y，z）→L为双态射，因为在（y，z）中y⊥z，β（x，·）是可加的，所以β（x，y）⊥β（x，z），且

因为在C2（x）中x⊥x，β（·，y）、β（·，z）是可加的，所以β（x，y）⊥β（x，y）、β（x，z）⊥β（x，z）且

又因为映射β（1，·）:（y，z）→L是可加的，所以β（1，y）⊥β（1，z），故

由L为效应代数知:β（x，y）⊥β（1，z），β（x，z）⊥β（1，y）.

定义φ:E→L为

则φ为态射，且（φ·σ）（u，v）＝0＝β（u，v），其中u＝0或v＝0.由于

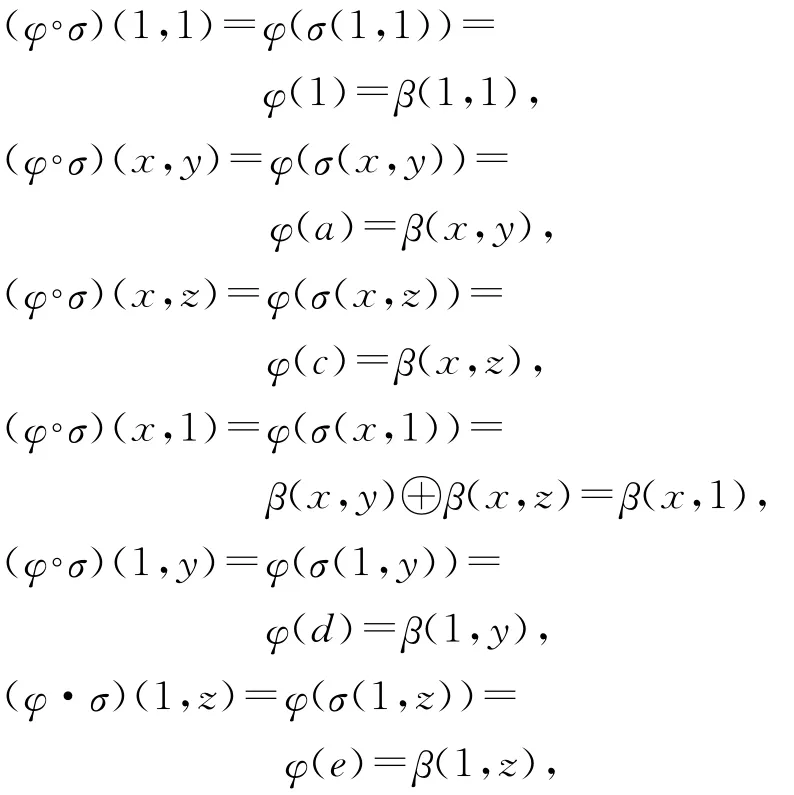
所以φ◦σ＝β，故定义5条件（1）成立.由于

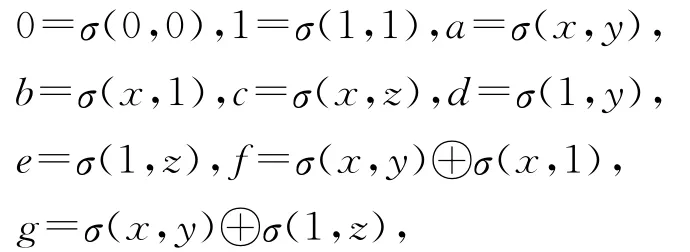
所以定义5中的条件（2）满足.因此，E为效应代数C2（x）与C′4（y，z）关于σ的张量积，即E＝C2（x）⊗σC′4（y，z）.证毕.

在集合C4（y，z）＝｛0，y，z，1｝上定义运算⊕，定义:

其中（u＝0，y，z，1），则（C4（y，z），⊕，0，1）为效应代数，且S（C4（y，z））＝｛φ｝，其中φ（0）＝0，φ（1）＝1，φ（y）＝0.5，φ（z）＝0.5.由文献［12］知:C4（y，z）是不可表示的效应代数.下面构造效应代数C2（x）与C4（y，z）的张量积，并讨论它的可表示性.

命题5 设E＝｛0，a，b，c，d，e，f，1｝，在集合E上定义运算⊕如下:

⊕0 a b c d e f 1 0 0 a b c d e f 1 a a c d e f 1 b b d c f e 1 c c e f 1 d d f e 1 e e 1 f f 1 1 1

则

（1）（E，⊕，0，1）为不可表示的效应代数，其态空间为S（E）＝｛φ｝，其中

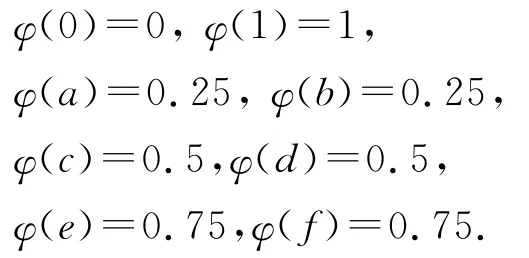
（2）E＝C2（x）⊗σC4（y，z），其中映射σ:C2（x）×C4（y，z）→E为

σ（u，v）＝0（u＝0或v＝0），

证明 （1）容易验证（E，⊕，0，1）为效应代数，φ∈S（E）.设φ∈S（E），由c⊕c＝1知1＝φ（1）＝φ（c⊕c）＝φ（c）＋φ（c），因此φ（c）＝0.5.类似可知φ（0）＝0，φ（1）＝1，φ（a）＝0.25，φ（b）＝0.25，φ（d）＝0.5，φ（e）＝0.75，φ（f）＝0.75.故φ＝φ，因此S（E）＝｛φ｝.由φ（a）＋φ（f）＝1，但由a与f不可加可知:定理1中条件（2）不成立，故E是不可表示的效应代数.

（2）容易验证σ为双态射.设L为任意效应代数，β:C2（x）×C4（y，z）→L为双态射.

因为在C4（y，z）中y⊥y、z⊥z，β（x，·）是可加的，所以β（x，y）⊥β（x，y），β（x，z）⊥β（x，z），且

因为在C2（x）中x⊥x，且映射β（·，1）是可加的，所以β（x，1）⊥β（x，1），且

1＝β（1，1）＝β（x⊕x，1）＝β（x，1）⊕β（x，1）.

由L为效应代数知:

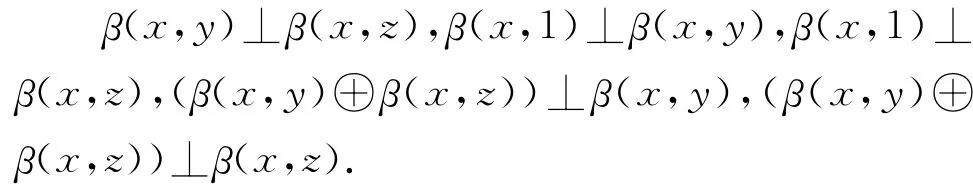
又因为在C2（x）中x⊥x，β（·，y）:C2（x）→L，β（·，z）:C2（x）→L是可加的，所以

定义φ:E→L为

则φ为态射，且（φ◦σ）（u，v）＝0＝β（u，v），其中u＝0或v＝0.因为

所以φ◦σ＝β，故定义5条件（1）成立.又因为0＝σ（0，0），a＝σ（x，y），b＝σ（x，z），c＝σ（x，1），1＝σ（1，1），d＝σ（x，y）⊕σ（x，z），e＝σ（x，y）⊕σ（x，1），f＝σ（x，y）⊕σ（x，1），所以定义5条件（2）成立.故由定义5知:E为效应代数C2（x）与C4（y，z）关于σ的张量积.

3 结语

本文证明了效应代数的张量积的唯一性，给出几类典型效应代数的张量积的具体构造，讨论了它们的可表示性.本文使用的方法对研究一般效应代数的张量积结构也有一定的参考价值.

［1］Foulis D J，Bennett M K.Effect algebras and unsharp quantum logics［J］.Foundations of Physics，1994，24（10）:1331-1352.

［2］Gudder S.Examples problems and results in effect algebras ［J］.International Journal of Theory Physics，1996，35（11）:2365-2376.

［3］Moreland T，Gudder S.Infima of Hilbert space effects［J］.Linear Algebra and its Applications，1999，286（1/3）:1-17.

［4］Gudder S.Lattice properties of quantum effects［J］.Journal of Mathematical Physics，1996，37（6）:2637-2642.

［5］Bugajski S，Gudder S，Pulmannova＇S.Convex effect algebras，state ordered effect algebras，and ordered linear spaces［J］.Journal of Mathematical Physics，2000，45（3）:371-388.

［6］Gudder S，Pulmannova＇S.Representation theorem for convex effect algebras［J］.Commentationes Mathematicae Universitatis Carolinae，1998，39（4）:645-659.

［7］Gheondea A，Gudder S.Sequential product of quantum effect［J］.Proceedings of the American Mathematical Society，2004，132（2）:503-512.

［8］Gheondea A，Gudder S，Jonas P.On the infimum of quantum effects［J］.Journal of Mathematical Physics，2005，46:062102.

［9］Du Hongke，Deng Chunyuan，Li Qihui.On the infimum problem of Hilbert space effects［J］.Science in China:Series A:Mathematics，2006，49（4）:545-556.

［10］陆玲，曹怀信，陈峥立，等.效应代数上态射的注记［J］.数学学报，2009，52（5）:958-960.

［11］曹怀信，陈峥立，郭志华，等.效应代数的表示［J］.中国科学:数学，2011，41（3）:279-286.

［12］张巧卫，曹怀信，陆玲.效应代数的表示及弱表示［J］.西北大学学报:自然科学版，2012，42（2）:198-202.

［13］曹怀信，郭志华，陈峥立，等.效应代数的表示理论［J］.中国科学:数学，2013，43（8）:853-846.

［14］张坤利，曹怀信，郭志华.效应代数上态的存在性［J］.数学学报，2013，56（3）:301-310.

［15］Dvureenskij A.Tensor product of difference posets and effect algebras［J］.International Journal of Theoretical Physics，1995，34（8）:1337-1448.