平衡k叉树网络的平均路径长度和链路效率

周异辉，邵志毅

（陕西师范大学 计算机科学学院，陕西 西安 710119）

网络的平均路径长度是网络中所有节点对之间的最短路径长度的平均值，是网络性能研究中的重要指标［1］.对通信网络而言，网络的平均路径长度在一定程度上反映节点的信息处理能力和信息的传递速率.如何快速有效地计算网络的平均路径长度是网络研究中不可避免的问题.文献［2-5］给出不同类型网络的平均路径长度.

树形结构是一类重要的非线性结构，它是数据元素按分支关系组织起来的结构，非常类似于自然界中的树.树形结构不仅为计算机应用中常出现的嵌套数据提供了自然的表示，也在解决文件管理、数据库、编译等系统的算法中得到广泛应用.平衡k叉树作为重要的网络结构被应用在通信网和嵌入式系统芯片的优化设计方案中.文献［6］给出基于二叉树表示的搜索空间数据缩减方法，文献［7］介绍了基于二叉树的有向环网络的最短路径算法，文献［8］给出平衡k叉树的离散数和完整度.本文给出n层平衡k叉树网络平均路径长度的精确计算公式，利用此公式研究平衡k叉树网络的链路效率，借助Matlab软件绘图对不同层数网络的平均路径长度和链路效率进行分析.

1 基本概念

首先给出平衡k叉树、网络的平均路径长度、链路效率等概念.

定义1［1］设k为正整数，平衡k叉树网络递归地定义为一个节点连接到k个也是k叉树的子树.一个节点称为根节点，它的度为k并且连接k个子树，后者连接到k个更多的子树上，以此类推.这种递归结束于一组称为叶子节点的节点上，叶子节点的度为1.所有中间节点经过k＋1条链路连接网络，因此平衡k叉树中节点的度仅可能是1、k、k＋1.

注1 （1）关于平衡二叉树的名称，不同的文献有不同的说法，例如文献［9］称其为满二叉树，文献［8］称其为完全二叉树.文献［9］中的完全二叉树与文献［8］中是完全不同的概念.本文采用文献［1］中的说法，仿照其中的平衡二叉树给出平衡k叉树的概念.图1中a、b、c、d分别是含有1层、2层、3层和4层的平衡二叉树.

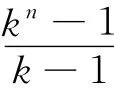
图1 1～4层的平衡二叉树Fig.1 Balanced binary tree with levels 1to 4

定义2［1］网络中两节点vi和vj之间经历边数最少的一条简单路径（经历的边各不相同）称为测地线.测地线的边数dij称为vi和vj之间的距离，或最短路径.

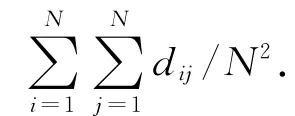
定义4［1］网络的链路效率定义为E＝1－L/M，这里M为网络的链路数，L为网络的平均路径长度.

2 平衡k叉树网络的平均路径长度和链路效率的计算

这里借助递推关系给出平衡k叉树网络平均路径长度和链路效率的计算公式，有关递推关系及特征方程法解递推关系的内容可参看文献［10］.

命题1 用Yk，n表示n层平衡k叉树网络的所有节点与根节点间的距离之和，则

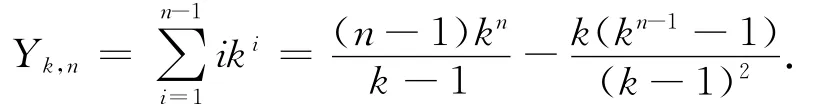
证明 因为n层平衡k叉树网络的第i（1≤i≤n）层有ki－1个节点，到根节点的距离为i－1，所以

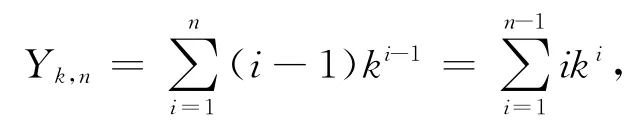
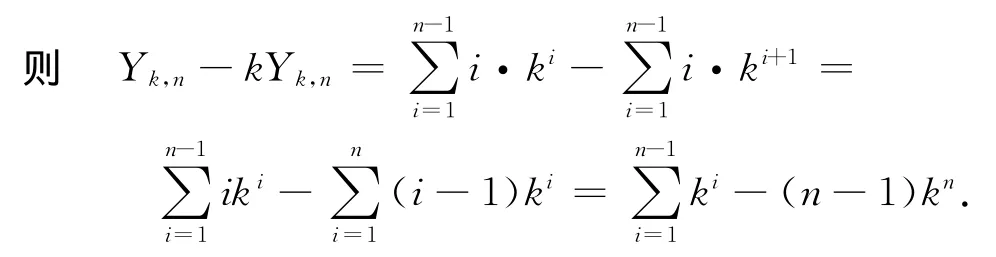
整理得

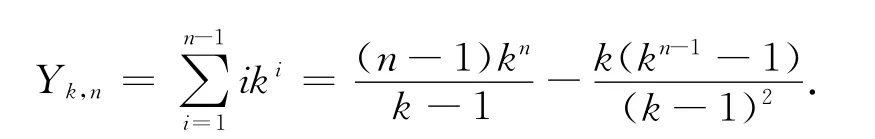
命题2 用Xk，n表示n层平衡k叉树网络的所有节点对之间的距离之和，则数列｛Xk，n｝n≥1满足递推关系

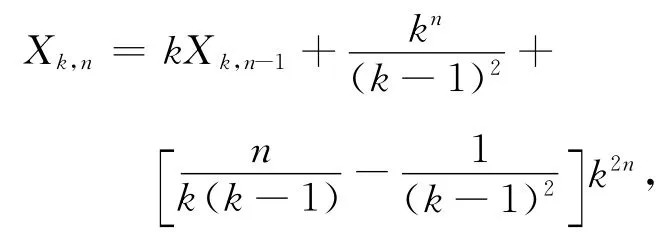
初始条件为Xk，1＝0.

证明 显然Xk，1＝0.将n层平衡k叉树的节点分为两类:根节点及与根节点连接的k个子树，各子树为（n－1）层平衡k叉树，编号依次为1，2，…，k.Xk，n为网络中所有节点对之间的距离之和，包括:（1）各子树内部节点间的距离之和kXk，n－1；（2）各子树节点与根节点的距离之和Yk，n；（3）各子树之间节点对距离之和.接下来计算（3）.

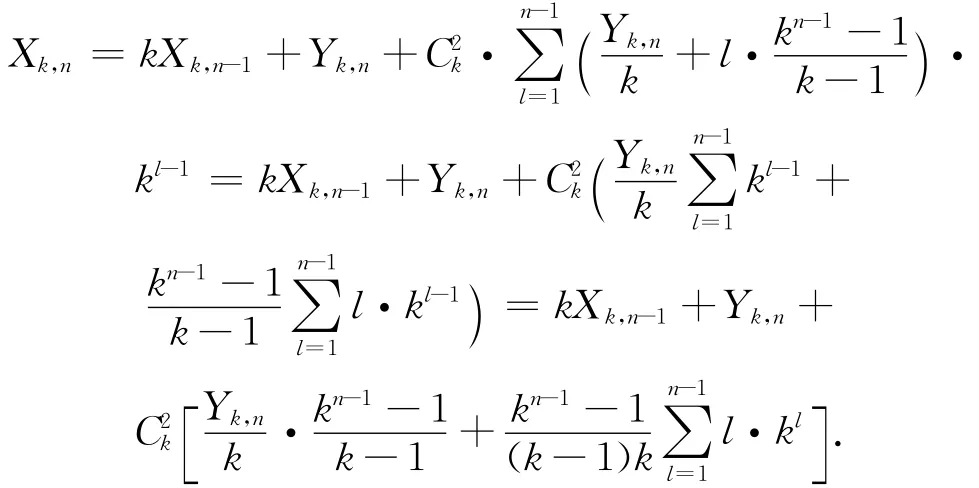
由命题1，得Xk，n＝kXk，n－1＋Yk，n＋

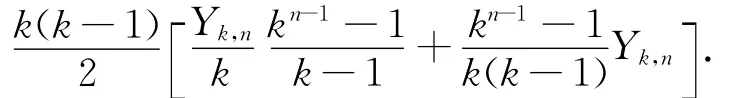
整理得Xk，n＝kXk，n－1＋kn－1Yk，n.

由命题1可知

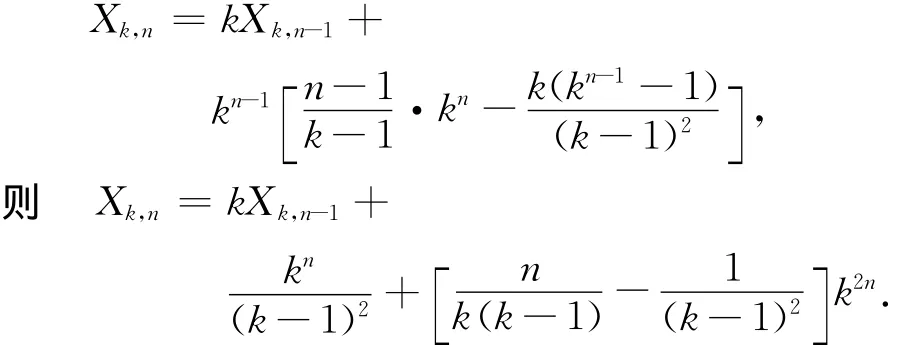
命题3 对于n层平衡k叉树，

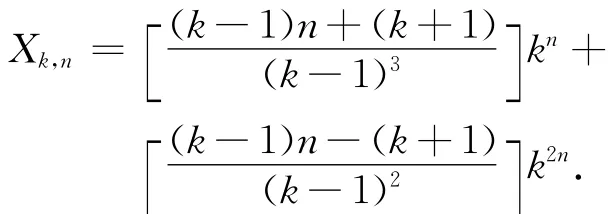
证明 用特征方程法解递推关系:

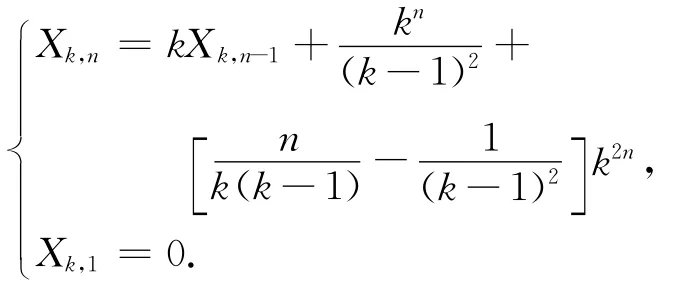
此为1阶常系数非齐次线性递推关系，对应的齐次递推关系为Xk，n＝kXk，n－1，特征方程为x－k＝0，特征根为x＝k，通解为Xk，n＝Ckn.由于

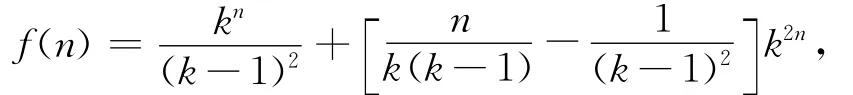
所以将原递推关系分成

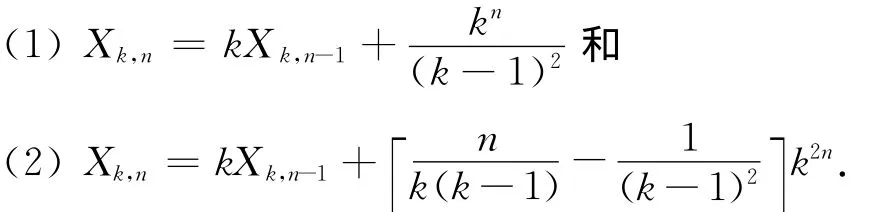
对（1），k是特征根，因此设特解为＝Ankn.将其代入递推关系（1），消去kn，得An＝A（n－1）＋.比较两端系数，解之，得.因此

对（2），k2不是特征根，因此设特解为＝（An＋B）k2n，代入递推关系（2），消去k2n－1，得（An＋B）k＝A（n－1）＋B＋比较两端系数解之，得

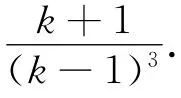
证毕.

根据平均路径长度和链路效率的计算公式，有定理1n层平衡k叉树网络的平均路径长度为

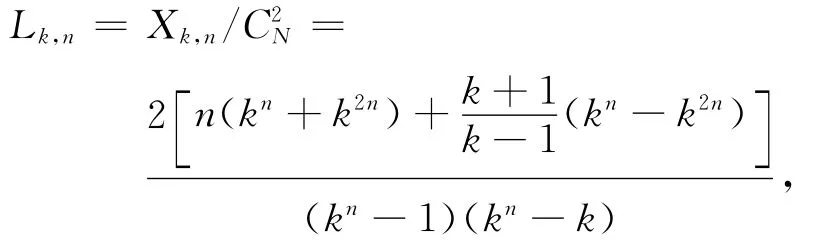
链路效率为

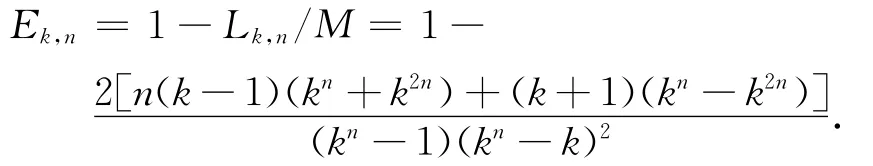
3 平均路径长度和链路效率与网络层数的关系

本节根据定理1中平均路径长度和链路效率的计算公式，利用Matlab软件绘图分析平衡k叉树网络中分叉数k和层数n对平均路径长度和链路效率的影响.

（1）图2给出平衡2叉、6叉、10叉树网络的平均路径长度.从图中可以看出，对同一个k值，平均路径长度关于层数n是增函数；对同一个n值，平均路径长度关于分叉数k是增函数.

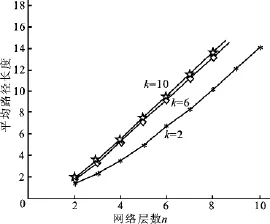
图2 平衡k叉树网络的平均路径长度Fig.2 Average path length of balanced k-ary tree

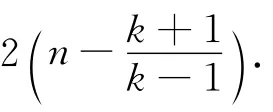
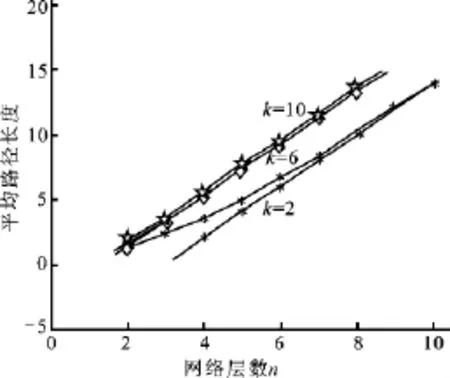
图3 平衡k叉树网络中平均路径长度与层数的近似线性关系Fig.3 The approximate linear relation of average path length and level number of balanced k-ary tree

（3）图4给出平衡2叉、6叉、10叉树网络的链路效率.从图中可以看出，对同一个k值，平均路径长度关于层数n是增函数，且n趋于无穷大时，链路效率趋近于1.

通过以上分析（1）和（3）可知，为了取得较小平均路径长度和较高的链路效率，k和n的值取得越大越好.但（2）表明，当k达到一定值时，取值再增加不会导致平均路径长度的过多增长和链路效率的大幅提高，因此k不需要选得过大.

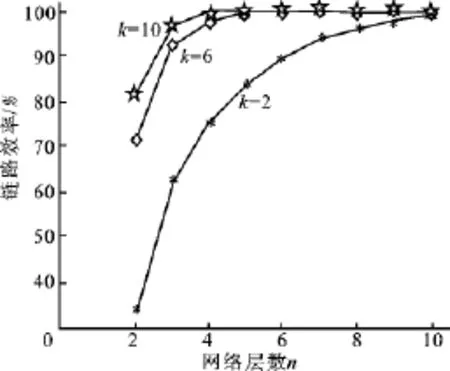
图4 平衡k叉树网络的链路效率Fig.4 Link efficiency of balanced k-ary tree

4 结语

本文通过对平衡k叉树网络进行深入分析，得到n层平衡k叉树网络中平均路径长度和链路效率的精确计算公式.根据计算公式，结合数学软件Matlab绘图，分析了网络层数的变化对平均路径长度和链路效率的影响.平均路径长度是网络层数n的增函数，且可用线性函数近似表示；链路效率也随网络层数n的增加而增加.

［1］Ted G Lewis.Network science:Theory and applications［M］.New Jersey:John Wiley and Sons，2009:70-85.

［2］何宇，赵洪利，姚曜，等.介数中心性和平均路径长度整合近似算法［J］.复杂系统与复杂性科学，2011，8（3）:44-53.

［3］董迎飞，王鼎兴，郑纬民.精确计算n维Mesh网络和n维Torus网络的平均路径长度［J］.计算机学报，1997，20（4）:376-379.

［4］陈浩，孙建华，金海.对等网络中平均路径长度的分析［J］.小型微型计算机系统，2006，27（3）:407-411.

［5］李瀛，山秀明，任勇.具有幂律度分布的因特网平均路径长度估计［J］.物理学报，2004，53（11）:3695-3700.

［6］邵楠，周雁舟，惠文涛，等.基于二叉树搜索空间缩减的测试数据生成［J］.计算机应用研究，2014，31（1）:188-191.

［7］陈业斌.基于二叉树的有向双环网络的最短路径算法［J］.华中科技大学学报:自然科学版，2009，37（4）:78-81.

［8］李银奎，段宝荣，陈忠.完全k叉树的离散数和完整度［J］.纯粹数学与应用数学，2011，27（3）:285-291.

［9］严蔚敏，吴伟民.数据结构（C语言版）［M］.北京:清华大学出版社，2011:118-155.

［10］卢开澄，卢华明.组合数学［M］.北京:清华大学出版社，2006:54-67.