90°弯管的流场中涡相互作用对声场的影响

李 丽，沈壮志＊，沈建中，郑 霞

（1陕西师范大学 物理学与信息技术学院，陕西省超声学重点实验室，陕西 西安 710119；2中国科学院 声学研究所，北京 100190）

近年来，弯管在农业、船舶业、航空业等机械设备上应用非常之广泛.管中黏性流体的流动具有较高的轴向压力梯度，对应单位轴向距离的压降具有较高的传热和传质速率［1］.通常情况下，弯曲管道内流场呈现出复杂的流动特性是由于受到流体运动方向、弯管弯曲程度及流体来流马赫数等因素的影响［2］.1927年，Dean［3］首次提出圆形截面弯管内存在二次流.它是指在主流速度和几何边界条件一定的情况下，黏性流体作曲线运动时所产生的一种有规律的伴随运动.弯管中的二次流主要指不可压缩流体在弯管内流动时，由于离心力的作用而形成的反向对称涡旋［4］.流体的运动是非定常的有涡运动，涡的非定常运动激发声波在流体介质中传播形成声场［5］.由于涡的复杂性，Zabusky等［6－7］运用周线动力学对各种涡斑的运动规律及其相互作用进行了研究.孟国庆等［8］应用Khirchoff涡斑模型研究了方腔中漩涡之间的相互作用，就涡势能和Palin势能进行了讨论.Powell［9］指出低马赫数下声来自不定常的涡运动，这些促进了涡声理论的迅猛发展.人们逐渐意识到涡旋对于构成湍流和诱发噪声必不可少.因此，研究涡声理论对涡激噪声的控制和消声理论的发展具有非常重要的意义.

龚斌［1］等人对90°圆形截面弯管内的流动情况进行了大涡模拟研究，结果表明不同角度截面速度场中二次流形成两个主涡，涡核随流线向管中心移动.樊洪明［10］等人对90°弯曲圆管内流动的数值模拟进行了研究，证明湍流大涡模拟方法适合于边界形状复杂，存在各向异性的大尺度涡的流动仿真.湛含辉［4］等人研究了90°弯管内二次流，得到了弯管中的迪恩涡随着雷诺数的增加，流体从层流到湍流的过程中，先出现涡核，然后涡核开始外扩，最后涡核显著外扩的现象.虽然之前的研究者们均对直角弯管中流场的涡进行了一定的数值研究和理论分析，然而却没有对弯管中涡相互作用产生声场的规律进行更加深入的研究.因此，本文在研究弯管流场的基础上进行了声场模拟，给出弯管中涡相互作用产生声场的变化规律，以及与之相应的声压随时间变化的关系.

1 计算模型与方法

1.1 计算模型

如图1所示，模拟对象主要由3部分组成，分别为入口段、出口段和弯管段.出、入口段的长度L均为50mm，弯管段的曲率半径D为90mm，弯曲的角度θ为90°，此直角弯管的管子直径d为20mm，并在弯管段截取了5个观测截面（θ＝0°、30°、45°、60°和90°的截面），分别观察了5个面上速度场和声场的变化情况.

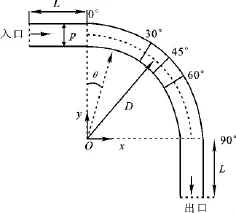
图1 90°弯管的数值计算模型Fig.1 Numerical calculation model of 90°curved tube

1.2 计算方法

1.2.1 大涡模拟控制方程 大涡模拟是一种典型的湍流数值模拟方法［11］，它介于直接模拟与Reynolds平均法之间.用瞬时的Navier-Stokes方程直接模拟湍流中的大尺度涡.小尺度涡则通过大尺度涡的瞬时Navier-Stokes方程体现出来.

通过处理瞬态下的Navier-Stokes方程可得大涡模拟的控制方程如下［11］:

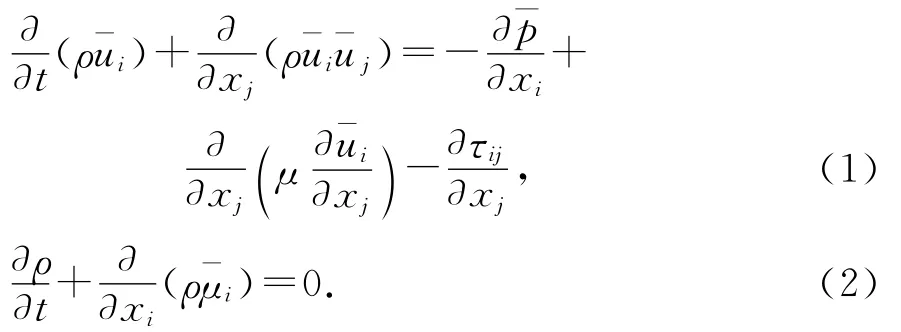
上式中τij被称为亚格子尺度应力，定义为

根据Smagorinsky的基本假设，得出

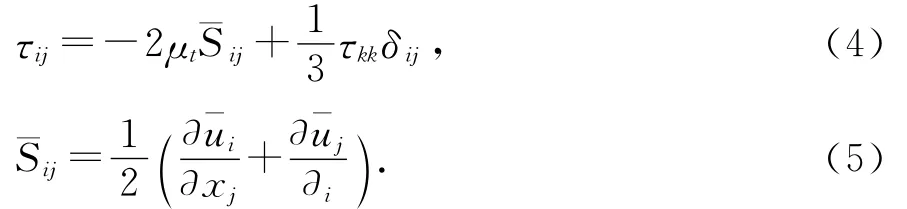
其中μt为亚格子尺度的湍动黏度，其可用下式进行计算

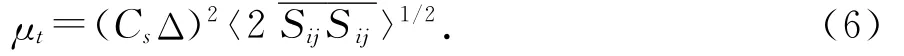
式中，Cs＝0.1，为Smagorinsky常数.

1.2.2 声模拟法 Lighthill最早提出气动声学理论.1969年，Ffowcs Williams和Hawkings运用广义理论函数推导出静止流体中做任意运动控制面的发声方程，即著名的FW-H方程［12］，如下所示:

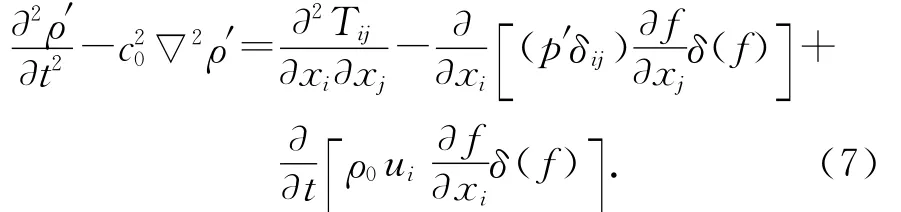
其中上式方程右边第一项是四极子声源，第二项是偶极子声源，第三项是单极子声源.四极子声源只存在于运动固体表面之外，在表面内为零；偶极子声源和单极子声源仅在固体表面上产生.（7）式的解可用自由表面格林函数求得.解包括面积分与体积分，如下式所示:

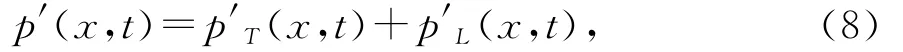
式中

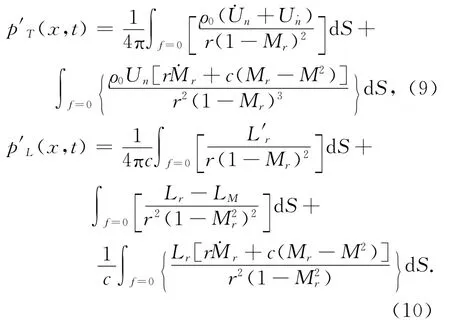
2 计算结果与讨论

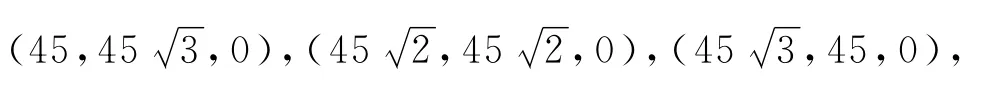
2.1 不同截面弯管的速度场和声场分布

2.1.1 不同截面弯管的速度场分布 由于t＝70 ms时刻的速度场二次流比较明显，因此选取此时刻不同截面的速度场进行比较，如图2所示，分别为θ＝0°、30°、45°、60°、90°的截面速度分布矢量图.在θ＝0°的截面上，流体的流动方向没有发生明显的变化.这是由于流体还没有受到弯曲段的影响.在θ＝30°的截面上，弯管内壁的压力比θ＝0°截面的压力有所增大，在离心力作用下内壁附近的轴向压力开始减小，外壁附近的压力开始增大，外侧流速减小.由于存在离心力，横剖面内产生了二次流，弯管中心的流体向外扩散，速度较高的流体向弯管内壁面流动，因此外壁附近出现了一对小涡.当θ＝45°时，涡的大小比之前的略为明显.在二次流的作用下，内壁附近的高速流体会穿过横截面中心向外壁运动，而上下壁面附近的低速流会沿壁面向内运动.在θ＝60°的截面上，外壁面附近的轴向压力不断增加，而流体速度不断减小.由于主流的高速流体向外壁面流动，向外壁流动的二次流向内壁面流动，从而导致涡旋的产生.在θ＝90°的截面上，二次流速度较大，已经出现一对涡心靠近内侧壁面的涡流，这是由于外侧壁面附近的压力大于内侧壁面，推挤流体向内侧壁面流动。故可得结论为:随着角度θ的增加，弯管中各个面的涡旋越来越明显，且出现的涡旋由弯管外侧向内侧移动.

图2 不同截面速度分布矢量图Fig.2 The vector diagram of velocity distribution with different angles

2.1.2 不同横截面弯管的声场分布 如图3所示在θ＝0°、30°、45°、60°、90°的截面上，声压峰值分别为1.61×105Pa，2.02×105Pa，2.43×105Pa，3.23×105Pa，3.58×105Pa，依次呈递增趋势.由此可知，随着角度θ的不断变大，声压峰值也在不断变大.在θ＝90°截面上，声压峰值达到最大值.这说明了在θ＝90°截面上涡与涡之间的相互作用最明显.由此可知，弯管中流场在一定的条件下产生二次流，其会影响流体的流动速度和产生漩涡，涡之间的相互融合和分裂产生了声辐射进而改变了声场的变化规律.

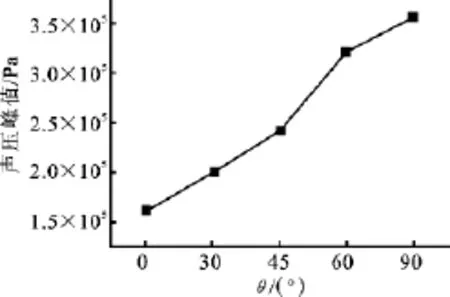
图3 声压峰值随θ角度的变化图Fig.3 The peak of sound pressure withθvariation diagram

2.2 同一截面弯管的速度场和声场分布

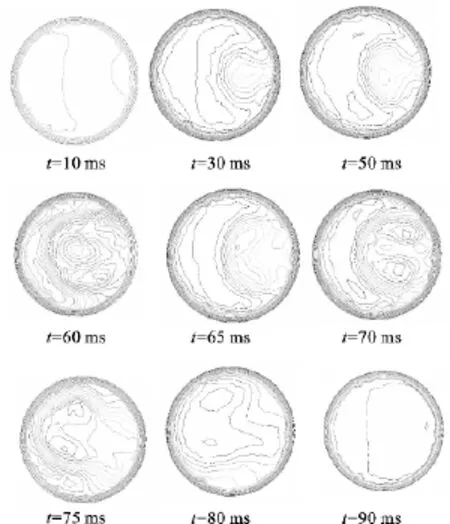
图4 不同时刻速度分布云图Fig.4 The contours of velocity distribution at different time

2.2.1 同一横截面不同时间弯管速度场分布 据以上分析可知，在90°截面上速度场的涡较明显，故选取该截面的不同时刻进行观察，发现该截面的涡随时间的变化而变化，如图4所示，在t＝0～50ms时间段内，截面的速度场开始没有涡，随着时间的推移，逐渐地出现了一个涡；在t＝50～65ms的时间内，一个涡慢慢地分裂为两个涡；t在65～70ms时间段内，截面上的两个涡分裂为三个涡；然后t在70～80ms的时间段内，三个涡又逐渐地融合为两个涡；最后t在80～90ms的时间段，截面上的两个涡又融合为一个涡，在此时刻之后，整个流场保持稳定，基本不发生任何变化.总之，在整个时间段的变化过程中，涡发生了一系列的演化，其中t＝70ms时刻，截面上的二次流最强，涡最多且最复杂.在融合的过程中，涡的位置在不断地由管外侧向内侧移动，这是由于随着时间的推移，在离心力的作用下，管中外侧壁面附近的压力不断地增大，推挤流体向内壁面流动，因此涡会随着时间慢慢由外壁面向内壁面移动.故可得如下结论:随时间不断变化，同一截面速度场中的涡经历了5个演变过程.先由一个分裂为两个，接着由两个变为3个，又由3个融合为两个，再由两个融合为一个，最后速度场保持稳定.

2.2.2 同一横截面不同时间弯管声场分布 如图5所示，a、b、c、d、e分别为θ＝0°、30°、45°、60°、90°截面的声压随时间变化关系图.从图中可以看出，t在0～50ms时间内，声压的振幅有一定的波动，但振幅波动很小，这是由于在这段时间内，该面上的湍流情况较复杂，在二次流的作用下，出现了涡，但是这些涡还没有开始融合或分裂，因此这段时间会有小波的振幅；t在50～130ms时间内，声压随时间不断地增大到某一程度后又开始减小，约在t＝70ms时声压出现最大值，是因为在这段时间里，流场中的大涡相互融合或分裂较明显；在t＞130ms时，声压基本无变化，其值约等于零，说明此时流场中的涡基本不发生相互作用.总之，在涡由分裂和融合到保持不变的整个过程中声压由小变大再到保持不变.

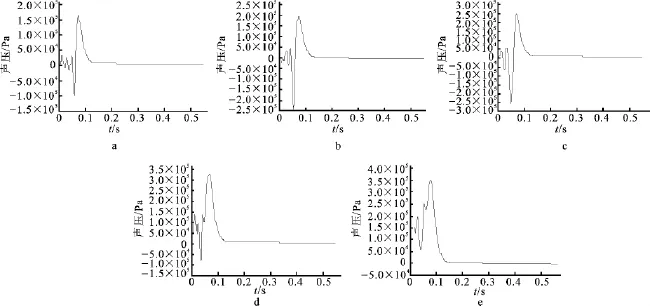
图5 声压随时间的变化图Fig.5 The sound pressure with time variation diagram

3 结论

本文基于有限元体积法的计算流体动力学fluent软件对90°弯管的流场和声场进行了数值研究.采用大涡模型对流体的湍流流动进行有限元模拟，并利用Fluent14.5中的SIMPLE算法实施计算，得到了如下结论:

（1）在t＝70ms时，随着角度θ不断增加，弯管中各个面的涡旋越来越明显，且出现的涡旋由弯管的外壁向内壁移动.由于二次流的作用，整个弯曲段呈现外壁面压力大速度小，内壁面压力小速度大的现象.

（2）在θ＝90°截面上，随着时间的不断变化，同一横截面速度场中的涡缓慢地由一个分裂为两个，由两个变为3个，接着又由3个融合为两个，再由两个融合为一个，最终速度场保持稳定.

（3）在二次流的作用下，流场出现了漩涡，其相互之间融合或分裂时出现声压，声压在整个过程中先产生小波动，然后在大涡的相互作用下产生较大的声压，最后流场处于稳定的同时声场也趋于稳定.本文选取的5个截面中，在θ＝0°～90°截面上，声压峰值呈递增的趋势，θ＝90°时达到最大值，该截面上产生的声压值最大.

本文主要研究了流场中的涡与涡间相互作用对声场产生的影响，这对90°圆形截面弯管的设计和优化提供了一定的理论依据和参考.

［1］龚斌，刘喜兴，杨帅，等.90°圆形截面弯管内流动的大涡模拟［J］.过程工程学报，2013，13（5）:760-765.

［2］丁珏，翁培奋.90°弯管内流动的理论模型及流动特性的数值研究［J］.计算力学学报，2004，21（3）:315-321.

［3］Dean W R.Note on the motion of fluid in a curved pipe［J］.Philosophical Magazine，1927，4（2）:223-238.

［4］湛含辉，朱辉，陈津端，等.90°弯管内二次流的数值模拟［J］.锅炉技术，2010，41（4）:1-5.

［5］刘晓宙，刘应中，繆国平.方腔中多个涡斑运动的数值模拟［J］.上海交通大学学报:自然科学版，2001，35（4）:527-531.

［6］Deam G S，Zabusky N J.Vortex waves:stationary“V states”interactions，recurrence and breaking［J］.Physical Review Letters，1978，40（13）:859-862.

［7］Zabusky N J，Hughes M H，Roberts K V.Contour dynamics for the Euler equations in two-dimensions［J］.Journal of Computational Physics，1979，30（1）:96-106.

［8］孟国庆，吴立新，黄永念.方腔中的漩涡运动［J］.水动力学研究与进展，1995，10（4）:451-456.

［9］刘晓宙，刘应中，廖国平，等.二维涡斑的运动发声［J］.声学技术，2001，20（1）:10-12.

［10］樊洪明，张达明，赵耀华，等.90°弯曲圆管内流动的数值模拟［J］.北京工业大学学报:自然科学版，2007，33（2）:174-177.

［11］王福军.计算流体动力学分析:CFD软件原理与应用［M］.北京:清华大学出版社，2005:139-142.

［12］Zhang Nan，Shen Hongcui，Yao Huizhi.Numerical simulation of cavity flow induced noise by LES and FW-H acoustic analogy ［J］.International Conference on Hydrodynamics，2010，22（5）:242-247.