丁羟包覆层力学特性及本构模型研究

杨晓红，周长省，常武军，吴 婧

（1.南京理工大学 机械工程学院，南京210094；2.航天东方红卫星有限公司，北京100094）

丁羟包履层是以丁羟粘合剂固化体系为基体材料，掺入耐烧蚀的固体填料及键合剂、增塑剂等组分构成的橡胶类复合材料。因其延伸率高，与复合推进剂粘接性能好，烧蚀率低，力学及工艺性能好而被广泛应用于复合固体推进剂装药的包覆，从而控制装药燃烧面的变化规律以满足内弹道性能的要求，且可使装药和燃烧室壳体粘接牢固，并起到缓冲推进剂与壳体之间应力的作用。然而，在固化降温的热应力及运输、撞击、振动、点火冲击等过程中产生的复杂载荷的作用下，装药会出现药柱与包覆层粘接界面脱粘的可能，同时固体填料的加入也降低了丁羟包覆层的力学性能，也易于出现裂纹等缺陷。因此，掌握其力学响应特征及本构模型是深入研究和应用该包覆层材料的基础。

近年来，包覆层的材料特性及其力学性能得到了国内外的关注。王永昌［1］采用正交试验，研究了不同类型的填料对丁羟包覆层材料力学性能的影响规律。常武军［2－3］采用单轴拉伸试验，研究了HTPB／IPDI固化胶片弹性基体的力学行为，并建立了超弹性本构模型。李冬［4］采用单轴拉伸实验，研究了不同温度及应变率下三元乙丙橡胶包覆层的拉伸力学性能。Frogley［5］研究了碳纳米管对橡胶类包覆层力学性能的补强作用。王广［6］等在数值研究复合推进剂／衬层界面脱粘过程时将衬层材料视为线弹性体。孟红磊［7］将包履层简化为线弹性体研究了不同类型包覆层材料对自由装填药柱结构完整性的影响规律。而丁羟橡胶包覆层易于产生大变形且力学行为具有明显的非线性特性，有关其本构模型的报道较少。本文采用单轴拉伸实验方法，研究了该包履层材料在拉伸载荷作用下的力学特性，基于4种超弹性本构模型预示了其应力－应变曲线变化规律，获取了本构参数并对比分析了各模型的适用性和精度，确定了有效描述丁羟包覆层力学行为的本构模型，为数值分析研究装药／包覆层界面脱粘断裂行为提供了可靠的性能参数和理论依据。

1 超弹性本构模型

丁羟橡胶包覆层具有大变形、超弹性等力学特性，可认为是近似不可压材料。橡胶类材料常用的超弹性本构模型有：Neo－Hookean模型、Yeoh模型、Mooney－Rivlin模型、Ogden模型等。超弹性本构模型可通过应变能函数与工程应力－应变之间的关系导出，材料的应变能函数W可用Green张量B的不变量表示为

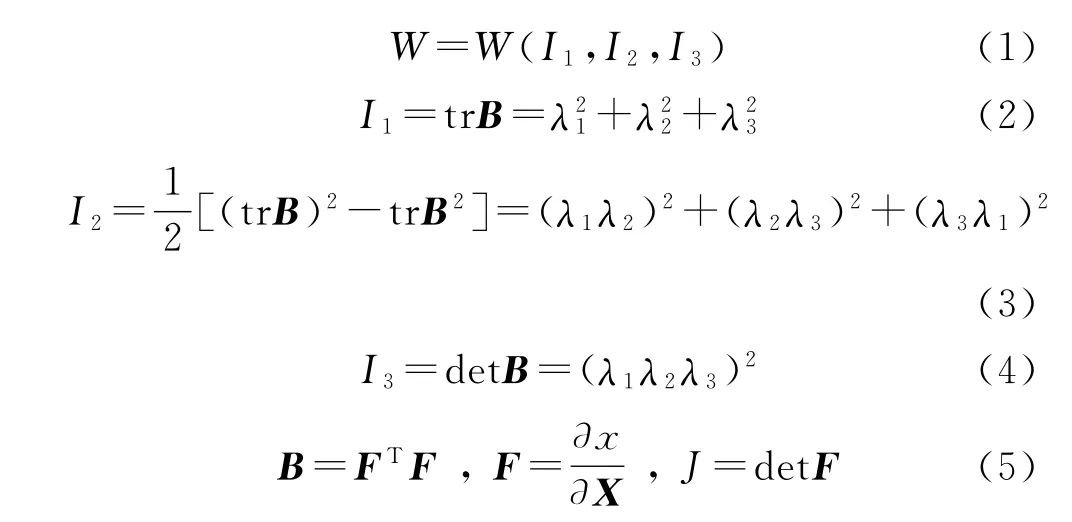
式中：F为变形梯度，x为空间坐标，X为物质坐标，J为变形后和变形前的体积比。对于纯均匀的应变，材料的主应力σti与其主伸长比λi之间的关系为

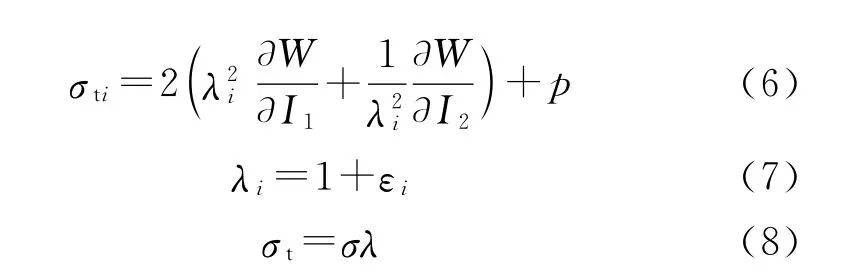
式中：p为静水压力，σt为真实应力，λi为主伸长比，σ为工程应力，ε为工程应变，i＝1，2，3。由式（6）可得主应力差为

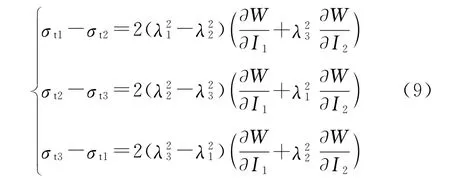
单轴加载条件下，当材料为不可压缩，且1方向是拉伸方向，则I3＝（λ1λ2λ3）2＝1，λ2＝λ3，σ2＝σ3＝0，由式（8）知σt2＝σt3＝0，将式（7）、式（8）代入式（9）可得：

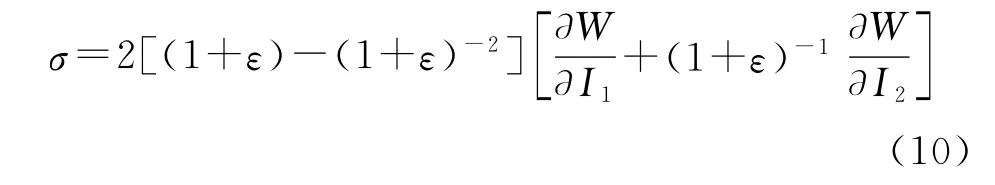
根据式（10），利用应变能函数可得出其工程应力－应变方程，再通过对实验数据的最小二乘拟合便可确定超弹性模型的参数［3］。

1.1 Neo－Hookean模型

Neo－Hookean模型的函数表达式为

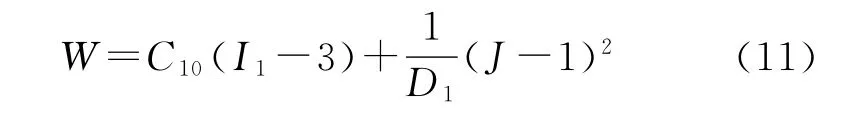
式中：C10为材料参数，D1为决定材料可压缩性的常数，变形时因丁羟包覆层可看作是不可压缩的，则J＝1，该模型形式简单，便于拟合，主要适用于小应变下材料的力学特性。

将式（11）代入式（10）求偏导，可得工程应力－应变方程为

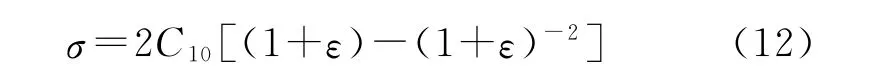
1.2 Yeoh模型

Yeoh应变能函数为

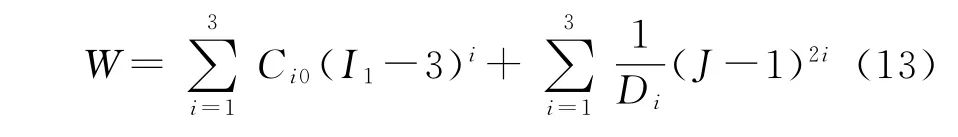
该本构模型可拟合出S型的应力－应变曲线。在小变形时，C10表示初始剪切模量；因系数C20一般为负值，即体现着中应变时材料的软化行为；而系数C30为正数，故大应变时材料会产生硬化行为，适用于较宽泛的变形范围，且由单向拉伸实验数据拟合的参数可用来预测其它变形条件下的力学行为［8］，因此该模型的应用可减少材料力学试验次数。

将式（13）代入式（10），得其工程应力 －应变关系为

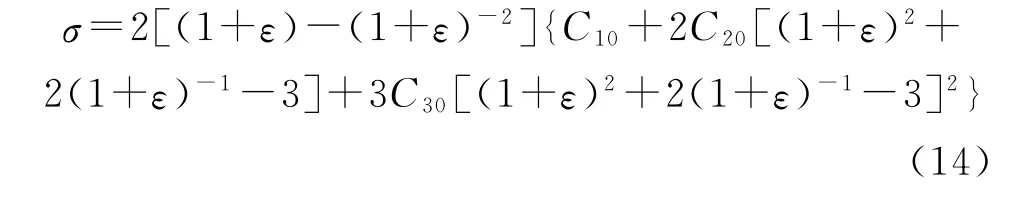
1.3 Mooney－Rivlin模型

其应变能函数为

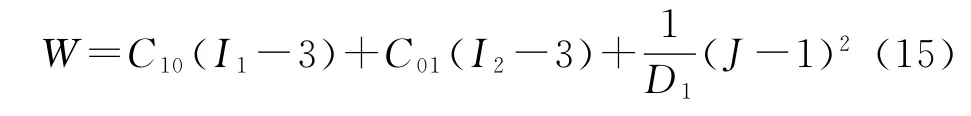
式中：C10，C01为材料的本构参数，材料不可压时J＝1。

将式（15）代入式（10）分别求偏导，可得单向拉伸时的工程应力－应变关系为

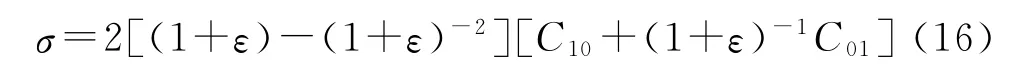
该模型形式简单、易于实现，可较好地适用于中等应变范围的拉伸应力－应变曲线，但不能很好地描述材料在压缩载荷下的力学行为。

1.4 Ogden模型

Odgen模型是基于主伸长比的应变能函数：

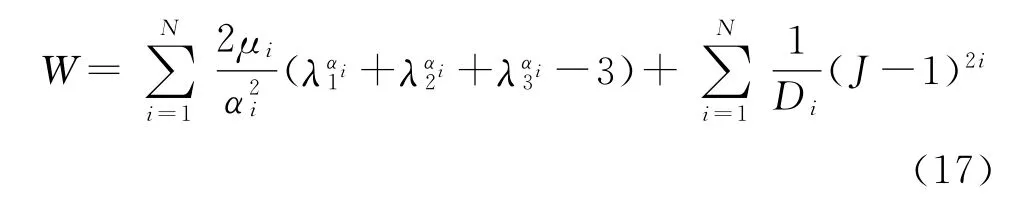
式中：材料不可压缩时J＝1；μi，αi，Di为材料参数，N为阶数，需根据材料实验采用非线性最小二乘法拟合获取。

将式（7）、式（17）及Green应变不变量表达式代入式（10），并分别求偏导，可得单轴拉伸下的工程应力－应变关系：

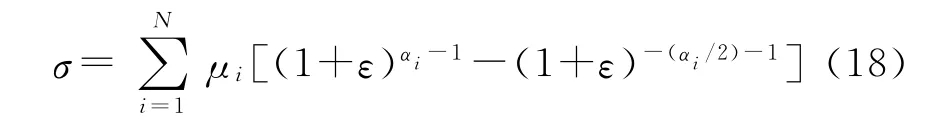
采用该模型拟合单轴拉伸实验数据获取的参数，可有效预测非常数剪切模量及轻微压缩等材料行为。

2 单轴拉伸实验

试验采用丁羟橡胶包覆层试样，其主要组分及质量分数为粘合剂78%～78.5%、键合剂4%～4.5%、固体填料9.5%～10.5%、增塑剂6%～6.5%、其它助剂0～2.5%。试样形状为板条状，尺寸为120mm×10mm×5mm，标距为100mm，在万能材料试验机上进行等速率单轴拉伸实验，实验环境为室温25℃、湿度45%，进行5次重复性实验，实验结果取平均值。文献［4］实验表明，50mm／min和100mm／min的拉伸速率下，该类橡胶材料的高弹特性可以体现出来，结合固体推进剂药柱的测试标准，选用100mm／min的拉伸速率。由于材料试验机的位移限制，拉伸过程中当应变达到300%时，便以100mm／min等速率卸载。

单轴拉伸实验结果如图1所示，实验曲线表明：丁羟橡胶包覆层具有显著的超弹特性，其延伸率在300%以上，此时的拉伸应力达0.8MPa。当应变小于30%时工程应力－应变曲线呈线性，弹性模量较大，初始弹性模量约为1.236 2MPa；随后材料出现非线性软化特性，弹性模量明显降低。而卸载过程中的力学行为主要表现为应变恢复具有迟滞现象，放置较长时间后应变即可恢复，这是由于丁羟橡胶包覆层存在一定的应力松弛和粘弹特性。

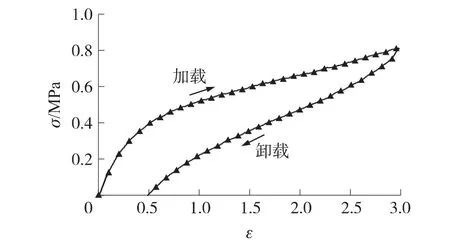
图1 丁羟包覆层拉伸载荷下工程应力－应变曲线

3 模型参数的获取与分析

对5组试验数据取均值后，得到平均的工程应力－应 变 曲 线，根 据 式 （12）、式 （14）、式 （16）及式（18），利用非线性最小二乘法分别对单轴拉伸实验数据进行曲线拟合，结果如图2所示。

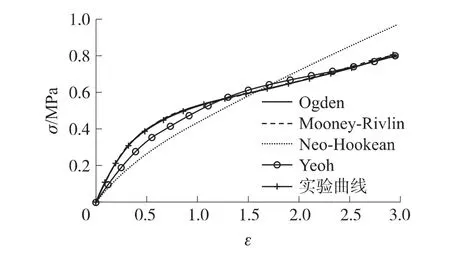
图2 单轴拉伸实验拟合曲线

Neo－Hookean模型参数：C10＝0.123 9；Yeoh模型参 数：C10＝0.157 6，C20＝ －0.004，C30＝0.000 1；Mooney－Rivlin模型参数：C10＝0.051 9，C01＝0.192 8；Ogden模型参数：μ1＝0.589 8，α1＝－2.758 7，μ2＝0.541 9，α2＝12.500，μ3＝－1.083 8，α3＝－24.999。

通过拟合结果可以发现，Neo－Hookean模型虽然形式简单易用，但拟合得到的曲线精度很差，难以预示丁羟橡胶包覆层的非线性特性。Yeoh模型在较小应变区间内拟合误差较大，在中应变和较大应变时与实验结果吻合较好，可以反映包履层较大变形时的力学行为，且由单轴拉伸实验数据拟合的参数可用来预测其它复杂变形条件下的力学行为，其中初始剪切模量C10＝0.157 6，系数C20为负数，表明了该材料中应变下的软化行为，C30为正数但数值很小，即在大应变下该材料的应变硬化行为不明显。这与复合固体推进剂的力学行为相近，因此丁羟包覆层与复合推进剂药柱的相容性好。Mooney－Rivlin模型和Ogden模型的拟合结果与拉伸试验数据吻合得很好，都能够很好地预示丁羟包覆层的材料特性，可应用于装药／包覆层结构完整性分析。

4 结论

①在准静态加载下，丁羟橡胶包覆层力学性能良好，具有很高的延伸率和拉伸强度，有显著的超弹性特征；卸载时力学行为表现为应变恢复的迟滞，即存在应力松弛和粘弹特性。

②Neo－Hookean模型难以表征丁羟橡胶包覆层的非线性特性，Yeoh模型可反映较大应变时的力学行为，而Mooney－Rivlin和Ogden超弹性本构模型能够很好地预示丁羟橡胶包覆层的拉伸力学特性。

③在丁羟包覆层的工程数值计算中，当为小应变问题时可视为线弹性模型，当发生有限变形时采用Mooney－Rivlin或Ogden超弹性模型较为准确。

［1］王永昌，黄庆，陈支厦.丁羟包覆层力学性能研究［J］.舰船防化，2010，5：18－22.WANG Yong－chang，HUANG Qing，CHEN Zhi－sha.Study on dynamic properties of HTPB liner［J］.Chemical Defence on Ships，2010，5：18－22.（in Chinese）

［2］常武军，鞠玉涛，胡少青.HTPB固化胶片的超弹性本构模型［J］.推进技术，2012，33（5）：795－798.CHANG Wu－jun，JU Yu－tao，HU Shao－qing.Research on hyperelastic constitutive model for HTPB crosslinked specimen［J］.Journal of Propulsion Technology，2012，33（5）：795－798.（in Chinese）

［3］常武军.复合固体推进剂细观损伤及其数值仿真研究［D］.南京：南京理工大学，2013.CHANG Wu－jun.Research on microstructural damage and its numerical simulation method for composite solid propellant［D］.Nanjing：Nanjing University of Science ＆Technology，2013.（in Chinese）

［4］李冬，陈竚，任黎.等.三元乙丙基固体推进剂包覆层拉伸性能影响因素研究［J］.化工新型材料，2011，29（9）：98－99.LI Dong，CHEN Zhu，REN Li，et al.Study on the influencing factors in the tensile property test of EPDM inhibitor for solid rocket propellant［J］.New Chemical Materials，2011，29（9）：98－99.（in Chinese）

［5］FROGLEY M D，RAVICH D，WAGNER H D.Mechanical properties of carbon nanoparticle－reinforced elastomers［J］.Composites Science and Technology，2003，63（9）：1 647－1 654.

［6］王广，赵奇国，武文明.复合固体推进剂／衬层粘接界面细观结构数值建模及脱粘过程模拟［J］.科学技术与工程，2012，12（30）：7 972－7 979.WANG Guang，ZHAO Qi－guo，WU Wen－ming.Mesostucture numerical modeling and debonding procedure simulation of composite solid propellant／liner bonding interface［J］.Science Technology and Engineering，2012，12（30）：7 972－7 979.（in Chinese）

［7］孟红磊.改性双基推进剂装药结构完整性数值仿真方法研究［D］.南京：南京理工大学，2012.MENG Hong－lei.Research on numerical simulation method of structure integrity analysis for modified double base propellant grain［D］.Nanjing：Nanjing University of Science ＆ Technology，2012.（in Chinese）

［8］YEOH O H.Some forms of the strain energy function for rubber［J］.Rubber Chemistry and Technology，1993，66（5）：754－771.