基于线性相关系数的RBV再入段增益调度设计

周晚萌，王 华，许江涛，崔乃刚

（1.国防科学技术大学 航天科学与工程学院，长沙410000；2.哈尔滨工程大学 航天与建筑工程学院，哈尔滨150001；3.哈尔滨工业大学 航天工程系，哈尔滨150001）

可重复使用助推飞行器（Reusable Boosted Vehicle，RBV）是根据空间任务需求［1］，重复使用并搭载不同上面级的一种运载飞行器。与传统的重复使用飞行器相比，RBV的维护成本低、可靠性高，可明显改善运载系统性能［2］，国内外有大量学者进行了相关研究［3］。

在RBV整个再入过程中，大气参数、飞行马赫数以及一些其它因素的变化会使模型参数的非线性特征更加突出，传统线性控制器很难满足控制要求，由此许多再入飞行器引入了增益调度技术（GainScheduling，GS）［4］。该技术最早由Shamma J S提出［5］，后来逐步发展为传统增益调度技术和基于线性变参数系统（LPV）的增益调度技术［6］。

虽然有大量关于增益调度点的选择以及调度点间隙测度与控制稳定性方面的理论研究［7］，但目前关于增益调度变量选取主要还是通过满足所选变量要体现对象的非线性特征，具有可测性等要求来实现。本文以面对称RBV的再入段为研究对象［8］，提出用线性相关系数作为选取调度变量的指标，并基于迭代理论和线性拟合理论对其加以证明，最终通过仿真验证了线性相关系数这一指标的合理性。

1 RBV线性化模型

本文首先对RBV再入过程进行系统建模，并对所建模型线性化，为解耦线性化模型设计控制系统，主要做出如下假设：

①未扰动运动中侧向运动学参数和纵向参数对时间的一阶导数很小，略去它们之间的乘积以及它们与其它小量的乘积；

②不考虑RBV的结构参数偏差对扰动运动的影响；

③小角度三角函数可以近似表示为sinθ≈θ，cosθ≈1；

④未扰动的运动参数、气动参数、结构参数和制导参数都不变。

基于以上假设，RBV线性化［9］后的运动学方程表示为

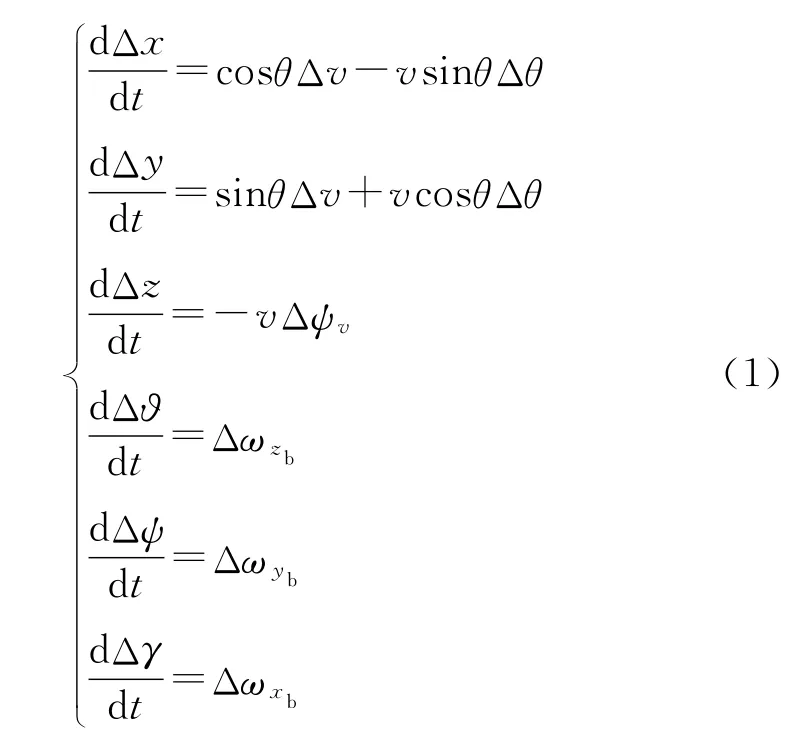
式中：θ为弹道倾角，ψv为弹道偏角，ϑ为俯仰角，ψ为偏航角，γ为滚转角。

补充关系线性化方程为

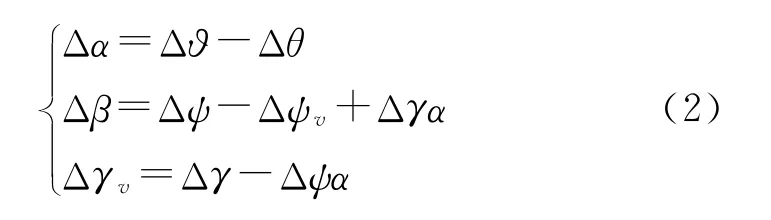
线性化后的RBV动力学方程表示为

式中：α，β分别为攻角、侧滑角；m，Jx，Jy，Jz分别为 RBV 质量和3个体轴的转动惯量分别为3个通道气动力系数对相关扰动的导数分别为三通道气动力矩系数对相关扰动的导数。

2 RBV控制器设计

2.1 控制器参数优化设计

本文以期望气动角为输入，加入控制器、增益限制、舵面延时各环节后的气动角为输出，RBV线性化模型三通道传递函数可统一表示为

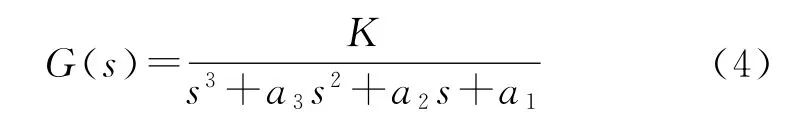
式中：K为增益系数，可以根据系统响应要求确定，具体的特征方程为

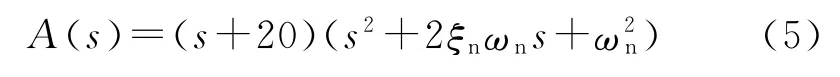
式中：ξn为阻尼系数，ωn为无阻尼自振角频率。令式（4）和式（5）的特征方程对应项系数相等，可以求出系统的控制器的初步参数。

进一步优化，优化的控制器参数集表示为k＝（kpkikdkd1kd2）T∈R5×1，其中kd1为反馈系数，kd2为角度反馈系数，kd为微分系数，kp为比例系数，ki为积分系数。

目标函数f为响应曲线超出响应约束范围的面积，表示为

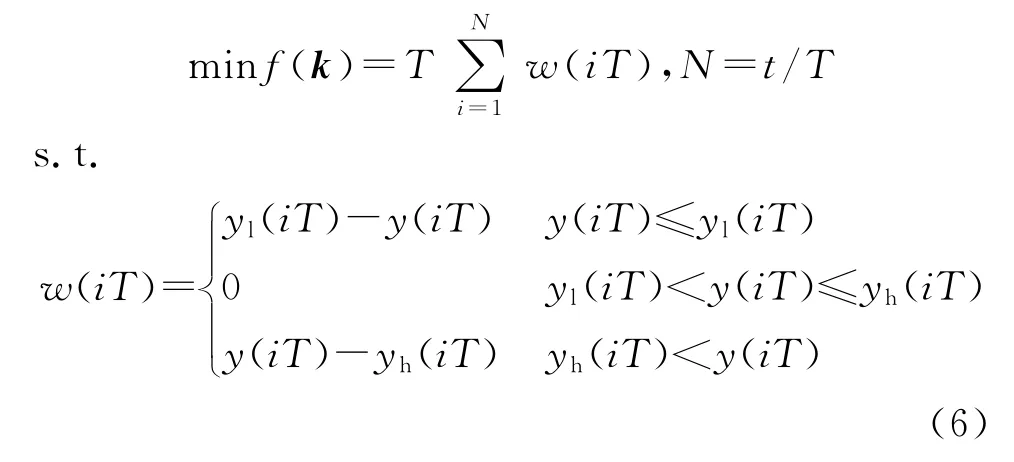
式中：t为总仿真时间，T为更新时间步长，y（iT）为iT时刻系统的响应输出，yl（iT）为输出约束下界，yh（iT）为输出约束上界，w（iT）为iT时刻系统的输出响应超出约束阈值的大小。

利用单纯形法对式（6）进行优化，具体的迭代步骤如下：

①给出n组保证阶跃响应稳定性初始设计控制参数k（n），定义反射系数λ＝1，收缩系数η＝0.5，扩张系数μ＝2，压缩系数σ＝0.5。

②将单纯形的n＋1个顶点按目标函数值的大小重新编号，使其满足：

③由下式计算除去最坏点以外各点组成图形的中心的目标值：

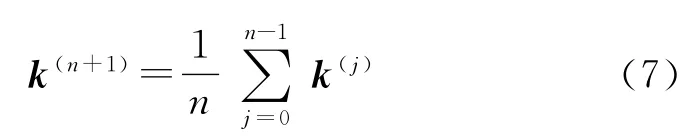
当满足式（8）时，停止迭代计算，否则转入下一步。

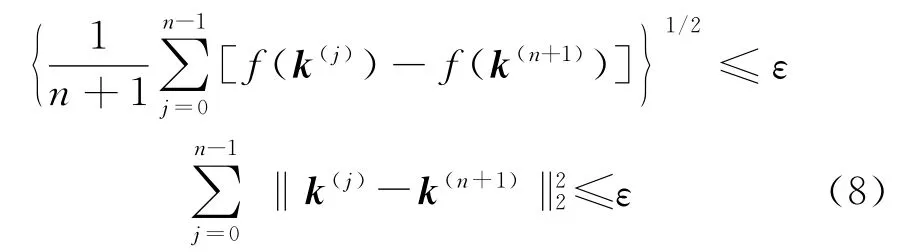
④反射计算：

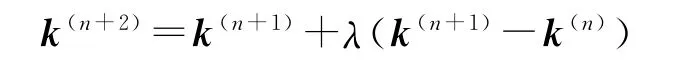
若f（k（n＋2））＜f（k（0）），转 入 第 ⑤ 步；若f（k（n＋2））＜f（k（n）），转入第⑥步；若f（k（n＋2））≥f（k（n）），转入第⑦步。

⑤扩张计算：

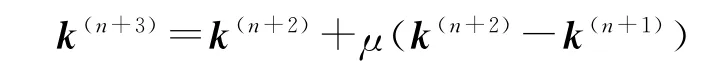
若满足f（k（n＋3））＜f（k（n＋2）），令k（n）＝k（n＋3），转入第②步，否则转入下一步。

⑥令k（n）＝k（n＋2），转入第②步。

⑦收缩计算：

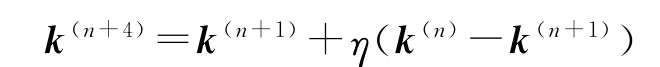
若满足f（k（n＋4））＜f（k（n）），令k（n）＝k（n＋4），转入第②步，否则转入下一步。

⑧压缩计算：

k（j）＝k（0）＋σ（k（j）－k（0）），j＝0，1，…，n，转入第②步。

2.2 优化结果分析

以滚转通道为例建立模型，如图1所示。Mxd1为副翼产生滚转力矩的效率。

该回路中共有5个系数分别是速率反馈系数kd1、角度反馈系数kd2、微分系数kd、比例系数kp和积分系数ki。令kd2＝1，kd1＝1，ki＝0，加入PD环节后利用极点配置法，获得kd＝－1.723×106，kp＝－9.091×106。

根据极点配置获得的PD系数设置6组初始控制器参数值，利用阶跃响应结果进行参数非线性优化。滚转通道的优化迭代阶跃响应曲线如图2所示。

由仿真结果可以看出，利用该方法能够有效设计这类控制器，整个阶跃响应的超调量下降了70%，过渡过程时间由1.5s减少至1.3s，优化效果显著。

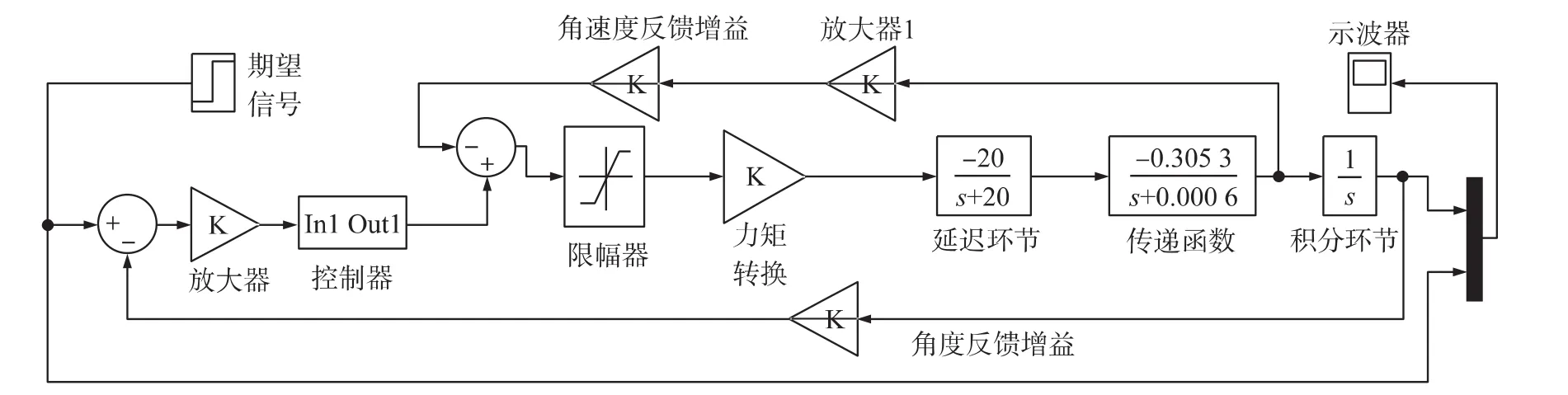
图1 滚转通道的简化模型

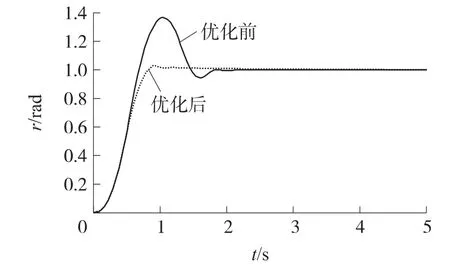
图2 参数优化过程响应曲线

3 增益调度系统设计

3.1 调度变量的选择指标分析

本文利用线性相关系数选取调度变量，下面证明线性相关系数与控制性能指标的正比关系。

设X为调度变量，且X∈R1×6，K5×5为对应的控制参数矩阵，将每个特征点处的5个控制系数组成一列，则可将5个特征点处的全部控制系数表示为K5×5＝（k1k2k3k4k5），K′∈R5×5。5个系数的相关系数计算公式如下：

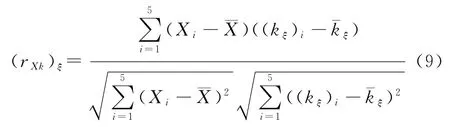
式中：ξ分别代表p，i，d，d1，d2。

利用单纯形法，对5个控制点处的控制参数集k1～k5分别进行优化设计，迭代过程中保证了目标函数达到最小f＊。定义特征点处控制器的控制性能为

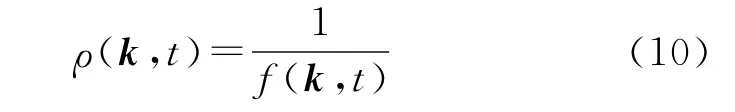
ρ越大表示控制器越接近期望性能，该指标量纲为rad－1。

期望的控制性能为ρ＊，控制器的控制性能为ρ′。两者之间的性能差距可表示为

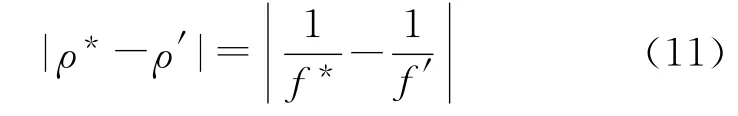
由协方差与数理统计相关理论，可知：

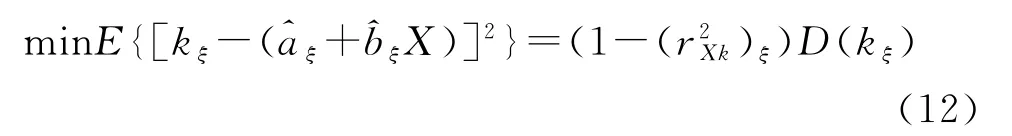
式中：kξ为设计控制器时的理论优化参数；为拟合系数；D（kξ）为系数kξ的方差。将上式5个等式求和，可得：

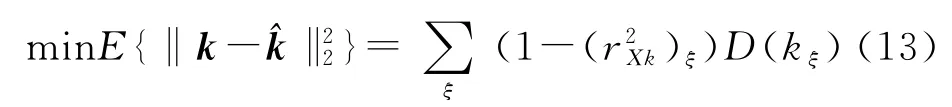
故当线性相关系数rXk越大，拟合形成的控制器系数与定点设计的控制器的控制参数k就越接近，就越小。由单纯形法优化最终收敛条件式（8）可知，因此有≤ε，即在理论优化控制系数k的临域内，目标函数收敛于局部最优f＊。因此有：

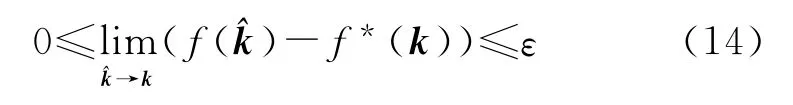
以ρ为半径作圆来形象化地表示控制能力，纵轴为控制器参数无量纲，横轴为增益调度变量的数值，其量纲由所选的调度变量确定，当两者的线性相关性越小，控制器的控制能力也越小，如图3所示。

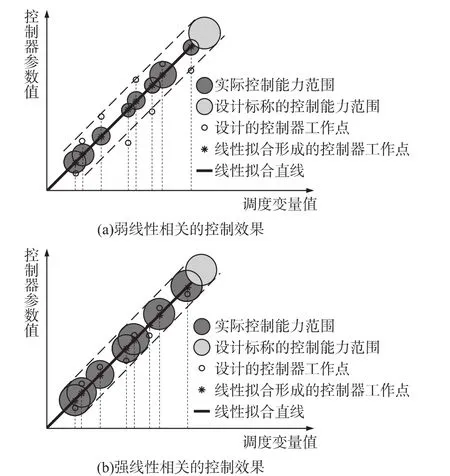
图3 线性相关性与控制系统鲁棒性的关系

3.2 增益调度控制系统设计

分析RBV整个再入制导过程，利用295s时的控制器对处于不同高度的RBV进行控制，以俯仰通道为例，可获得如图4所示的阶跃响应的曲线族。随着高度h的降低，由于气动效率的增加，超调量不断增加且上升时间缩短，过渡过程时间延长。

在47.45～54.1km的高度范围内选取6个特征点，除47.45km处的控制器外，还要根据气动参数的变化对其它高度处的5个特征点的控制器重新进行设计，重新整定后的控制器的阶跃响应曲线族如图5所示。最终3个通道调整后的控制器参数如表1所示。

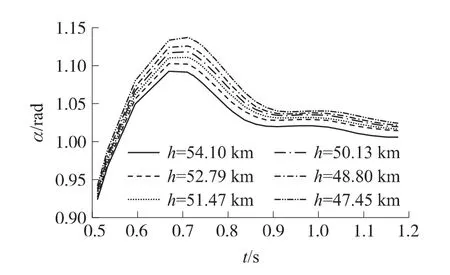
图4 同一控制器在不同特征点处的响应曲线

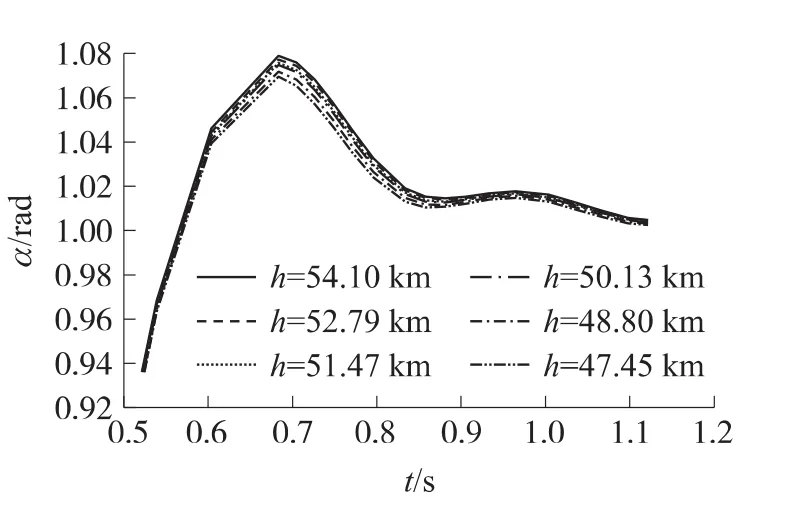
图5 调整控制器后在不同特征点处的响应曲线

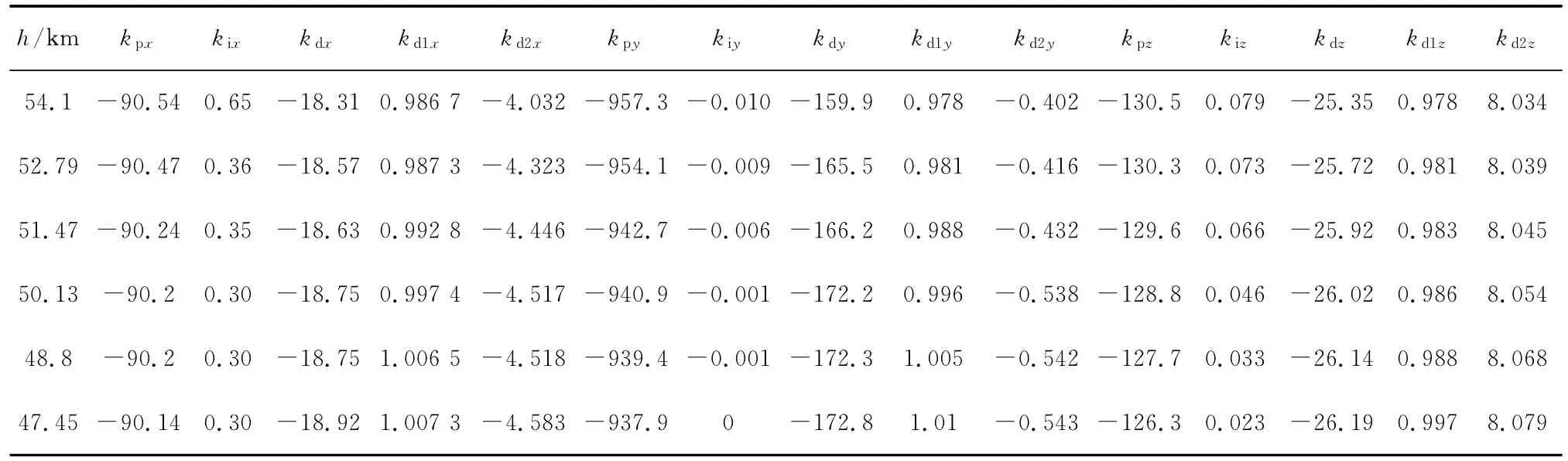
表1 不同特征点处的控制系数总表

将各组系数对应不同的调度系数进行插值，并计算响应的线性相关系数。通过计算滚转通道的比例系数与不同增益调度变量之间的线性相关系数可知，同一控制系数与不同调度变量间存在不同的线性相关性。同一调度变量与不同参数间的线性关系，如图6所示。从中可以看出调度变量与不同控制参数间存在不同的线性相关性。由图7可知，在不同的通道下同一组调度变量与控制系数之间存在不同的线性相关性。综合考虑以上3种对应关系的线性相关系数，选择马赫数作为滚转、偏航通道的调度变量，高度作为俯仰通道的调度变量。

在选择合适的调度变量之后，利用调度策略，将输入的调度变量对应的控制参数通过插值的方法解算出来，从而建立这一时刻的控制器。

3.3 增益调度系统仿真

将设计好的控制器参数装定入增益调度模块，给定期望姿态角并开始仿真。仿真过程中的所有气动参数都是根据参数插值环节获得，整个系统是时变系统。

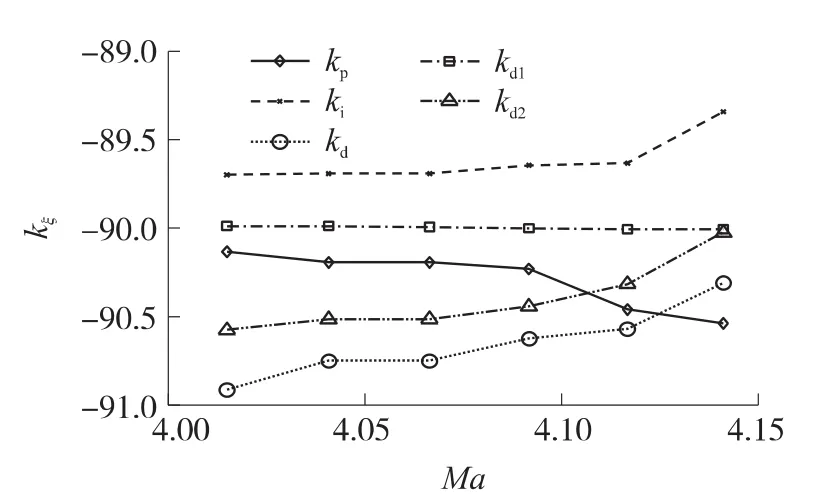
图6 马赫数与控制参数间的线性关系图

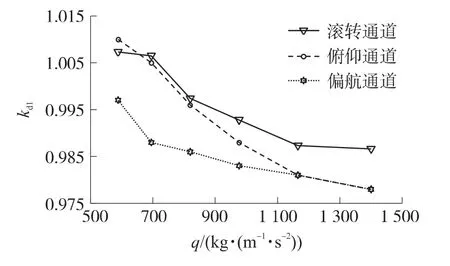
图7 动压与三通道反馈的线性关系图

仿真初始条件如下：初始时间295s，初始位置（125.46km，528.65km，0.789km），初 始 速度1 365.1m／s，速度倾角 3.726 9rad，速度偏角0.000 263rad，姿态角（4.405 5rad，0，0），姿态角速度0，质量30 500kg，转动惯量（90 000kg·m2，939 000kg·m2，923 000kg·m2）。

仿真结果，分别表示滚转角、侧滑角、攻角以及角速度在5s内的控制结果。

仿真结果如图8所示，由于滚转通道与其它通道存在耦合，因此存在小幅度波动。实际偏航角较好地跟踪了期望信号，虽然存在一个较小的控制延时误差，但误差不会积累。俯仰通道在1.2s之后呈现周期性震荡，最大偏差不超过0.3°。

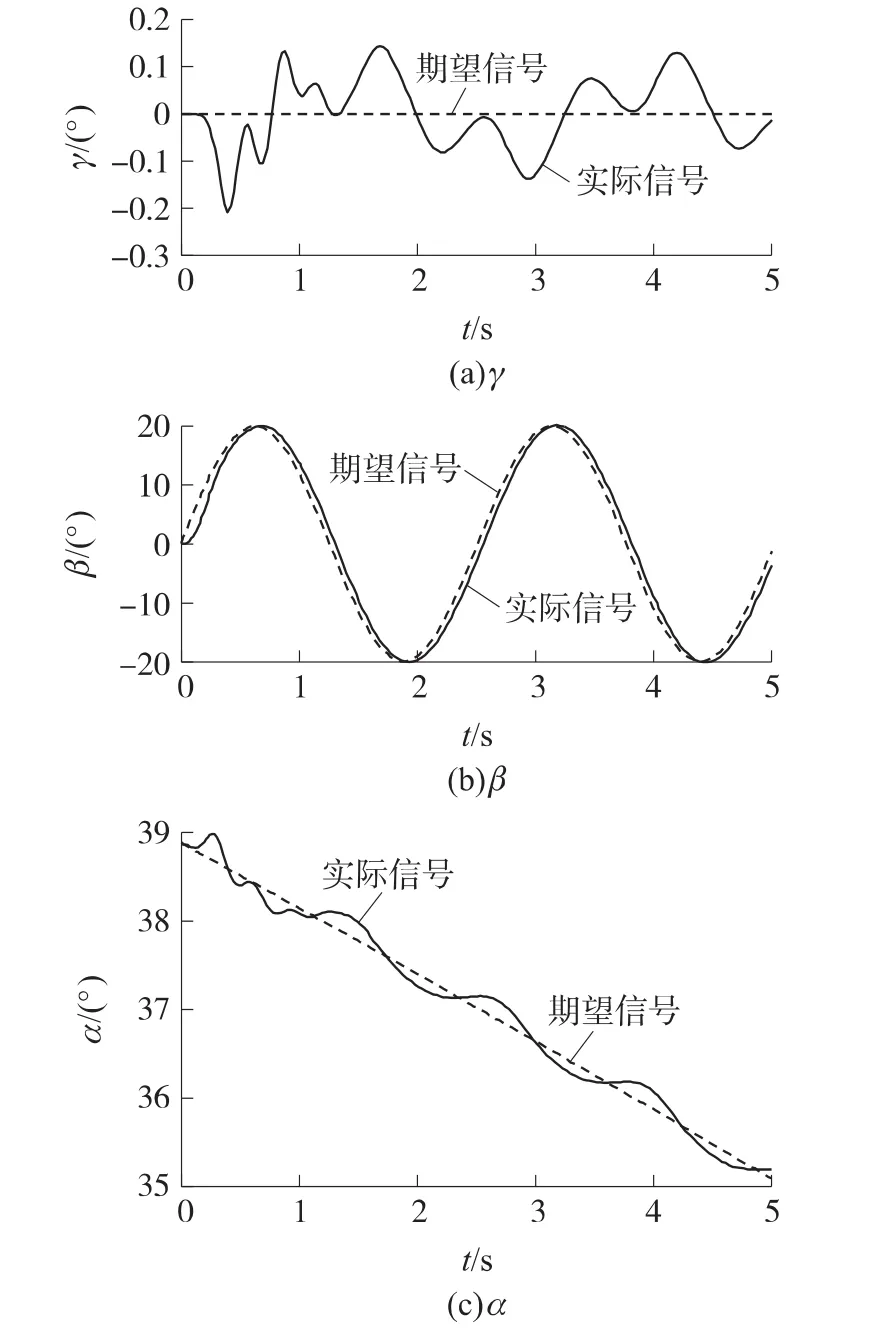
图8 姿态角的仿真结果

以上仿真结果表明，采用线性相关系数的方法选择调度变量，可以充分发挥增益调度系统的优越性，达到更好的控制效果。

4 结束语

本文以RBV为控制对象，基于线性相关系数进行再入段增益调度控制系统设计。

①采用单纯形法与极点配置组合优化方法设计并优化控制器参数，完成单个点处的线性控制器设计，提高了控制器设计精度和设计效率。整个阶跃响应的超调量下降了70%，过渡过程时间由1.5s减少至1.3s。

②基于传统增益调度方法，并根据参数优化的迭代收敛条件和概率统计中的拟合线性相关性理论，提出了反映不同调度变量控制性能的量化指标，证明并验证了基于线性相关系数的增益调度控制系统能很好地满足控制要求，最终仿真结果跟踪误差不超过0.3°。

［1］DENEU F，MALASSIGNE M.Promising solutions for fully reusable two－stage－to－orbit configurations［J］.Acta Astronautica，2005（56）：729－736.

［2］CARLO T，LAURENT B.RLV candidates for European future launchers preparatory programmer［J］.Acta Astronautica，2009（65）：40－46.

［3］许江涛，崔乃刚，陈阳阳，等.基于改进定点二乘的重复使用助推飞行器控制分配研究［J］.航空学报，2012，33（12）：2 269－2 276.XU Jiang－tao，CUI Na－gang，CHEN Yang－yang，et al.Research on control allocation based on improved fixed－point for reusable boosted vehicle［J］.Chinese Journal of Aeronautics，2012，33（12）：2 269－2 276.（in Chinese）

［4］RUGH W J，SHAMMA J S.Research on gain scheduling［J］.Automatica，2000（36）：1 401－1 425.

［5］MARCOS A，BALAS G J.Development of linear parameter varying models for aircraft［J］.Journal of Guidance，Control，and Dynamics，2004（27）：218－228.

［6］KENNETH H M.Selecting operating points for discrete－time gain scheduling［J］.Computers and Electrical Engineering，2003（29）：289－301.

［7］韩鹏鑫.可重复使用助推飞行器的导航、制导与控制方法研究［D］.哈尔滨：哈尔滨工业大学，2011.HAN Peng－xin.Study on the navigation guidance and control of reusable boost vehicle［D］.Harbin：Harbin Institute of Technology，2011.（in Chinese）

［8］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2011.QIAN Xing－fang，LIN Rui－xiong，ZHAO Ya－nan.Missile flight mechanics［M］.Beijing：Beijing Institute of Technology Press，2011.（in Chinese）