固定鸭舵式弹道修正弹二体系统建模

王 毅，宋卫东，佟德飞

（军械工程学院 火炮工程系，石家庄050003）

打击精确化是陆军在未来信息化战争中立足的基础，新型炮兵制导弹药的发展受到各国陆军的高度重视。弹道修正弹作为一种具有一定打击精度的新型制导弹药，自美国上世纪70年代中期提出以来取得了长足的发展。各国学者提出了制导炮弹的多种二维修正控制方式，大致可归为2类：基于气动力的修正控制和基于直接力的修正控制。基于气动力的二维修正常用的是基于鸭舵或正常舵的控制方式，该方式可连续提供用于修正的力和力矩。另外，基于摆动头锥的修正控制方式也属于该种类型［1－2］。基于直接力的修正控制方式通过在弹丸质心位置附近沿弹体圆周布置脉冲推冲器，利用脉冲推力矢量修正弹道轨迹，该方式具有响应速度快、控制方式简单的特点。

弹道修正引信是当前研究的热点。弹道修正引信在具备已有功能的基础上，扩展了弹道探测、弹道解算和修正控制等功能，仅采用弹道修正引信替换原有引信即可达到减小散布、提高精度的目的［3］。Clancy J A、Bybee T D等研制了基于固定鸭舵的弹道修正引信［4］，该引信采用修正组件与弹体具有不同的滚转角速度的单通道修正控制技术，克服了旋转稳定弹转速过高不易修正控制的问题。修正组件与弹体具有不同的滚转角速度，传统的六自由度刚体弹道模型不能有效地描述弹丸在飞行过程中的运动状态。针对该问题，Costello M建立了七自由度刚体弹道模型［5］，但该模型没有针对具体的修正模式进行研究，虽可用于基于固定鸭舵的弹道修正弹，但不能精确反映弹丸在飞行过程中的受力，也不能有效描述弹丸修正组件与弹体之间的相互作用。

对基于固定鸭舵的弹道修正引信，国内外进行了大量研究。郝永平、张嘉易等研究了舵片面积、翼展、翼型、舵偏角等因素与弹丸升力之间的关系，并分析了前置舵片对弹丸气动特性的影响［6－7］。纪秀玲等利用TVD格式求解N－S方程，采用双时间推进方法对带可旋转固定鸭舵的旋转弹丸的流场进行数值模拟，分析其俯仰特性随鸭舵方位角的变化规律［8］。Wernert P采用线性化理论分析了安装基于固定鸭舵的弹道修正引信的某型155mm旋转稳定弹的稳定性［9］，但未针对基于固定鸭舵的二维弹道修正弹进行仔细深入的建模分析。综上，迄今未有学者针对基于固定鸭舵的二维弹道修正弹的建模问题进行深入研究。

本文引入多刚体理论，将弹丸作为滚转角速度不同的2个刚体进行研究。针对修正组件气动外形不对称的问题，在修正组件质心建立新坐标系，分析其在弹丸飞行过程中的受力；应用多刚体理论，研究2个刚体间的相对运动关系和相互作用。在此基础上建立了描述弹丸飞行过程的七自由度弹道模型，并通过仿真验证了模型的正确性。

1 弹丸受力分析

图1所示为某弹道修正引信的外形图。舵1和舵3具有相同的舵偏角，但舵偏角方向不同，称其为一对差动舵；舵2与舵4舵偏角方向均相同，称其为一对操纵舵。引信通过螺纹连接弹体上，并与弹体同轴。在来流作用下，差动舵形成的导转力矩使引信头部产生与弹体方向相反的滚转角速度，而引信尾部将与弹体一同旋转。将转速不同的两部分作为不同的刚体进行分析，并分别将其称为修正组件和弹体，分别用下标f和a进行标记。

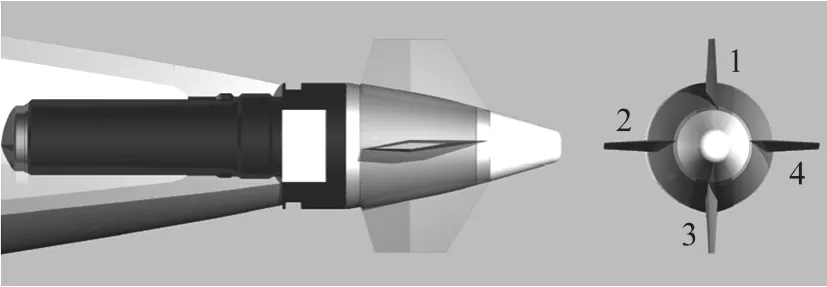
图1 引信舵片分布示意图

由于弹丸气动外形非对称，若来流速度大小一定，来流从不同方位吹向图1所示姿态的弹丸，弹丸所受气动力不同。在弹丸飞行过程中，弹丸轴线与弹丸质心速度矢量的夹角（以下称章动角δ）按二圆运动的规律变化，且修正组件绕弹丸轴线旋转，弹丸所受气动力不断变化，且比轴对称外形弹丸的受力复杂。

假设修正组件与弹体之间无气动耦合现象，将修正组件和弹体作为不同的刚体进行分析。

1.1 修正组件受力

引入修正组件体坐标系、修正组件速度坐标系，如图2所示。坐标系定义如下。

地面发射系Oxyz：坐标原点取发射点，Ox轴在发射点水平面内指向发射瞄准方向，Oy轴沿发射点的铅垂线向上，Oz轴垂直于Oxy平面，构成右手系。

修正组件体坐标系Ofxf1yf1zf1：坐标原点位于修正组件质心，Ofxf1沿修正组件轴线，Ofyf1在修正组件纵向对称面内垂直于Ofxf1；Ofxf1，Ofyf1，Ofzf1构成右手系。

修正组件速度坐标系Ofxf2yf2zf2：坐标原点位于修正组件质心，Ofxf2沿修正组件速度方向，Ofyf2在修正组件纵向对称面内垂直于Ofxf2；Ofxf2，Ofyf2，Ofzf2构成右手系。

G为弹丸质心，Gf和Ga分别为修正组件和弹体的质心，且分别距质心G的距离为lf和la，则有：

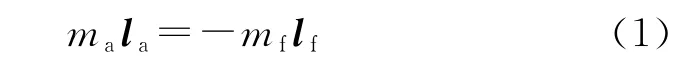
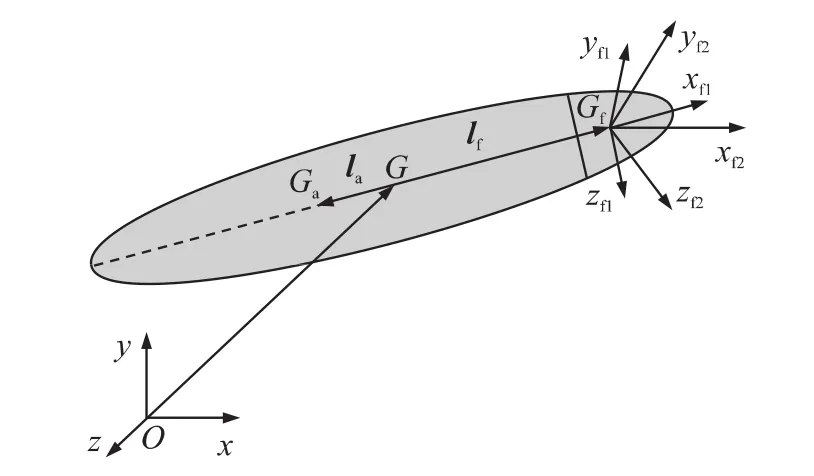
图2 坐标系定义

引入攻角αf、侧滑角βf，定义如下。

攻角αf：修正组件速度矢量在修正组件纵向对称面内的投影与Ofxf1轴的夹角，规定Ofxf1轴在上时攻角αf为正。

侧滑角βf：修正组件速度矢量与修正组件纵向对称面的夹角，规定速度矢量指向修正组件纵向对称面右侧时侧滑角βf为正。

几何关系方程为

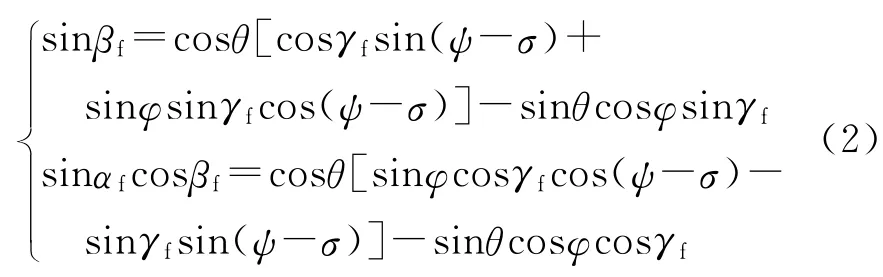
式中：φ，ψ，γf，θ，σ分别为修正组件的俯仰角、偏航角、滚转角、修正组件速度倾角和修正组件速度偏角。

通过攻角αf、侧滑角βf和马赫数Ma插值获得了气动参数后，经计算得到修正组件所受空气动力。

修正组件受力包括空气动力、重力和弹体对修正组件的力，弹体对修正组件的力Ffa＝（Ffa，xFfa，yFfa，z）T，Ffa，x，Ffa，y，Ffa，z为其在发射系下的分量。将修正组件受力投影到发射系中，有：

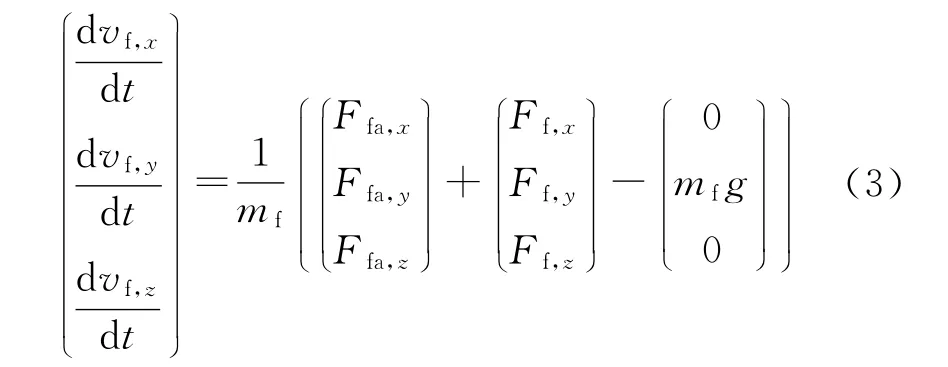
式 中：vf，x，vf，y，vf，z，Ff，x，Ff，y，Ff，z分 别 为 修 正 组 件质心速度和其所受空气动力在发射系中的分量，mf为修正组件的质量。

将修正组件所受气动力矩分解到准弹体坐标系，并在准弹体坐标系建立动力学方程：

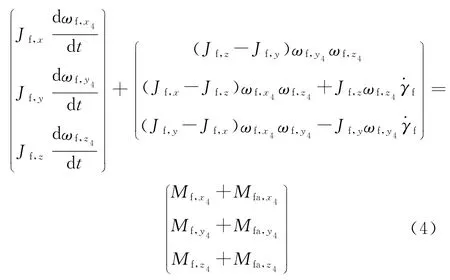
式中：Jf，x，Jf，y，Jf，z为修正组件相对弹丸质心的转动惯量；ωf，x4，ωf，y4，ωf，z4为修正组件角速度在准弹体 坐 标 系 中 的 分 量；Mf，x4，Mf，y4，Mf，z4，Mfa，x4，Mfa，y4，Mfa，z4分别为修正组件所受气动力矩和弹体对修正组件的力矩在准弹体坐标系中的分量。

1.2 弹体受力

弹体为旋成体气动外形，其受力和力矩相对简单。为便于受力，建立相应的坐标系，原点位于弹体的质心上。弹体质心运动方程为

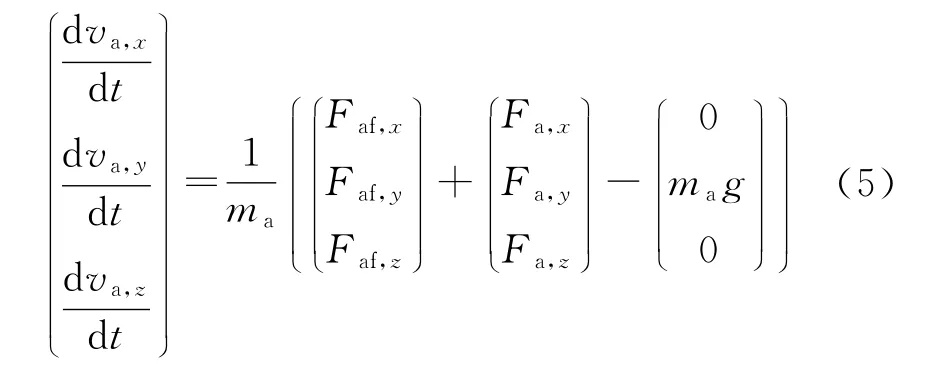
将弹体所受气动力矩分解到准弹体坐标系，并在准弹体坐标系建立动力学方程：

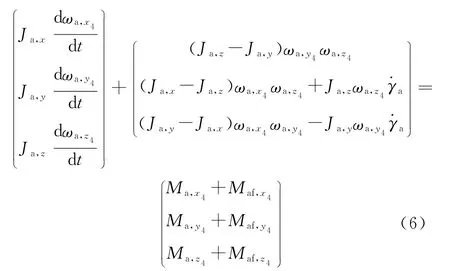
式中：Ja，x，Ja，y，Ja，z为弹体相对弹丸质心的转动惯量；ωa，x4，ωa，y4，ωa，z4为弹体角速度在准弹体坐标系中 的 分 量 ；Ma，x4，Ma，y4，Ma，z4，Maf，x4，Maf，y4，Maf，z4分别为弹体所受气动力矩和修正组件对弹体的力矩在准弹体坐标系中的分量。

2 二体运动分析

在轴承的约束下，修正组件和弹体具有相同的俯仰角速度和偏航角速度，即

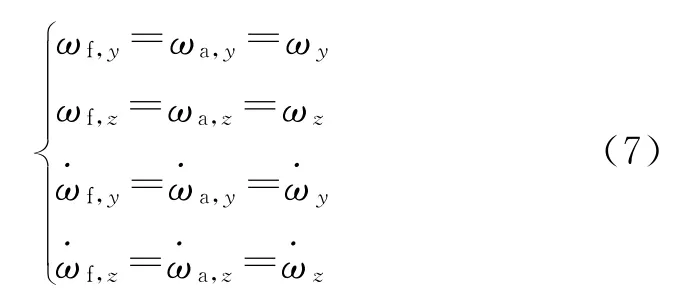
式中：ωy，ωz为发射系下弹丸绕质心的偏航角速度和俯仰角速度；，为其相应的偏航角速度和俯仰角加速度。

以弹丸质心为基点，则发射系下修正组件和弹体的质心速度矢量分别为

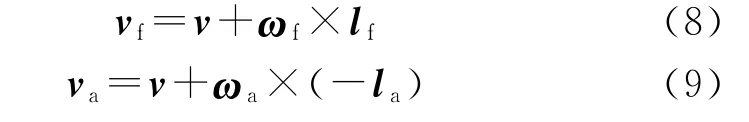
设弹丸质心加速度为a。以弹丸质心为基点，则修正组件和弹体的质心加速度矢量分别为

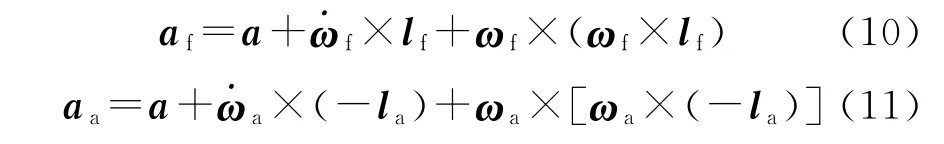
则由式（1）可得：

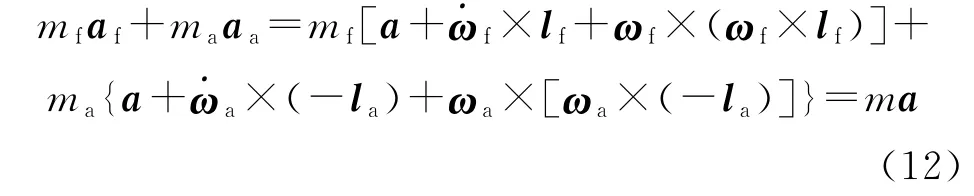
修正组件和弹体通过轴承连接，不计安装误差，两刚体同轴，且准弹体坐标系下偏航角速度和俯仰角速度 相 同，即ωf，y4＝ωa，y4＝ωy4，ωf，z4＝ωa，z4＝ωz4，在保证连接强度的条件下，两组件间通过轴承传递俯仰力矩和偏航力矩。由于轴承摩擦的存在，差动舵形成的导转力矩需要克服轴承的摩擦力矩使修正组件旋转；在修正过程中，制动器输出摩擦力矩改变修正组件转速从而调整弹体姿态。两摩擦力矩构成准弹体系中两组件间的轴向力矩。由式（6），可将式（3）和式（5）的第2个和第3个方程分别相加，并消去两刚体间的相互作用力矩，可得：

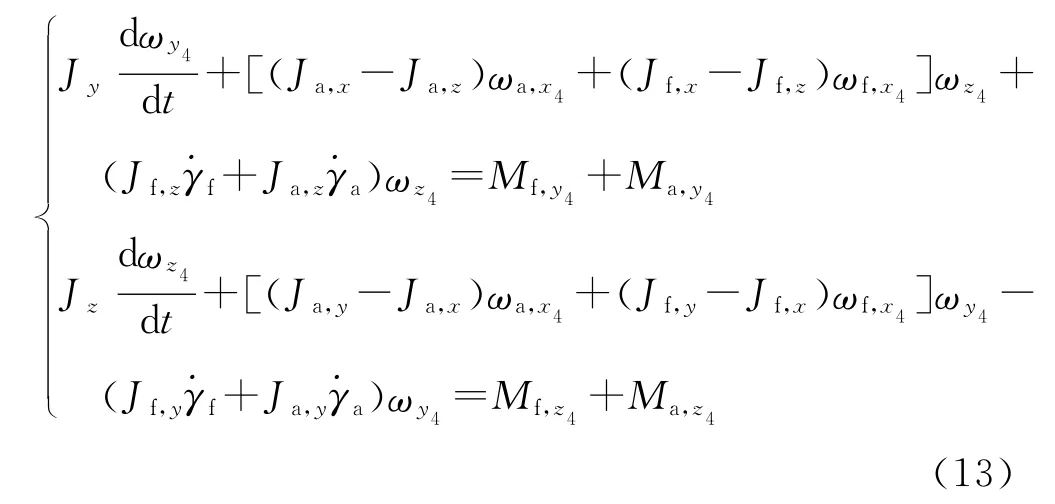
3 弹道建模

弹丸质心速度矢量为v＝（vxvyvz）T，由式（12）可得：

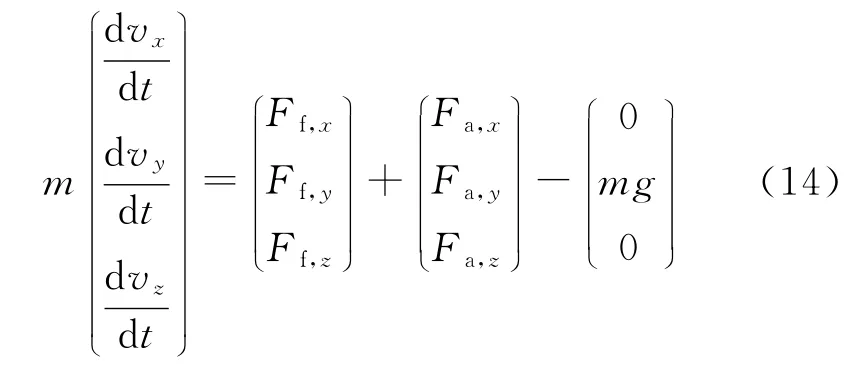
弹丸绕质心的角运动方程为

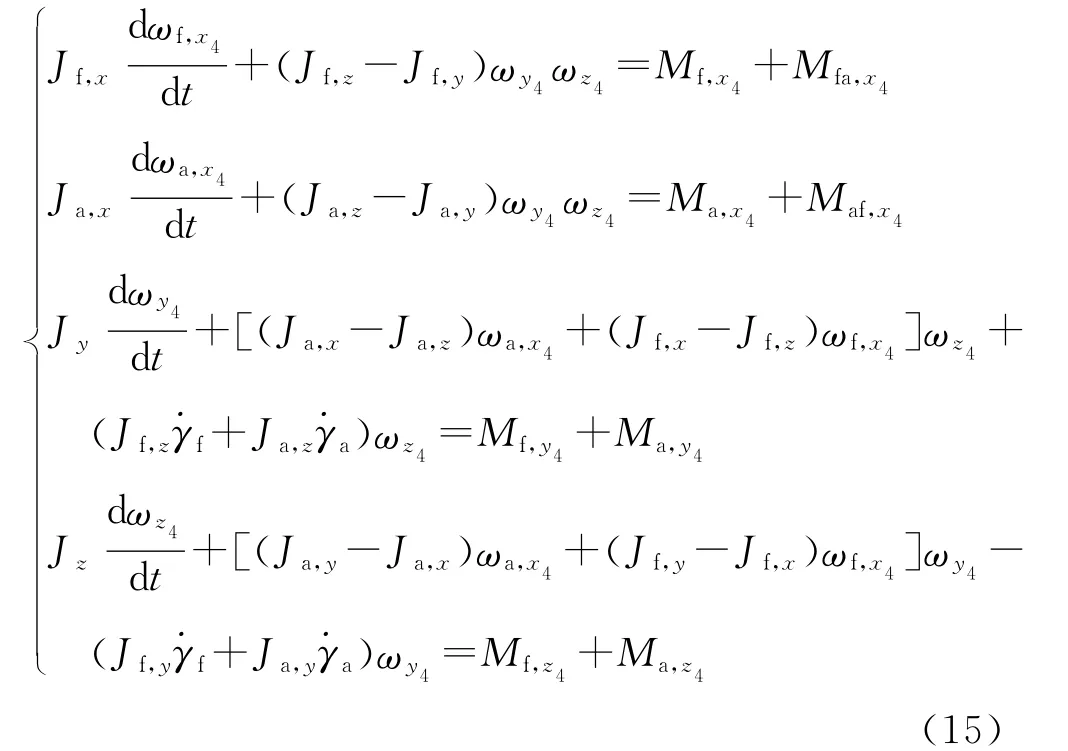
式中：Jy＝Jf，y＋Ja，y，Jz＝Jf，z＋Ja，z。

弹丸质心运动方程为

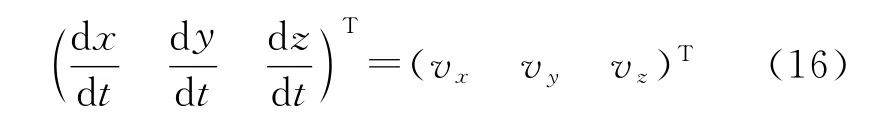
弹丸角运动方程为

综上，可得弹丸数学模型。由于修正组件与弹体滚转角速度不同，需要不同的方程进行描述，故可将该模型称为七自由度弹道模型。

4 仿真结果分析

采用某型炮弹的气动参数进行无控仿真，弹丸结构参数和仿真初始参数见表1。表中m、L、S、vi、A1、Ad分别为弹丸的质量、特征长度、特征面积、初速、射角和射向。仿真步长取0.001s，仿真初始位置取图1所示位置。

表1 弹丸结构参数和仿真初始参数

气象条件取标准气象。该弹丸为尾翼稳定的低速滚转弹丸，忽略马格努斯力和马格努斯力矩带来的影响。

连接修正组件与弹体的轴承是球轴承，其接触为点接触。两组件间的相对运动会使轴承滚珠发热膨胀，但轴承内外圈间存在间隙且轴承内外圈也同时产生不同程度的膨胀，其摩擦力与摩擦力矩不会有明显的变化，可认为其为常量，取摩擦力矩为0.01N·m。

4.1 相同舵偏角、不同舵片面积时仿真分析

采用舵偏角δd为4°、舵片面积比值为4∶5∶6时的3套气动参数进行仿真，仿真结果记为S1、S2、S3，见表2，表中Xm、Ym、Zm分别为射程、最大弹道高和侧偏。

由表2可知，随舵片面积的增大，弹丸弹道高和射程减小。

随舵片面积的增大，来流在舵片上的作用面积增大，使弹丸上所受阻力、升力和导转力矩增大。修正组件的转动惯量不变而导转力矩增大，导致修正组件的转速增大，如图3所示。舵片上所受升力作用于弹丸质心形成翻转力矩，增大弹丸的章动角δ，使弹丸的稳定性变差。随面积增大，弹丸章动角δ增大，如图4所示。

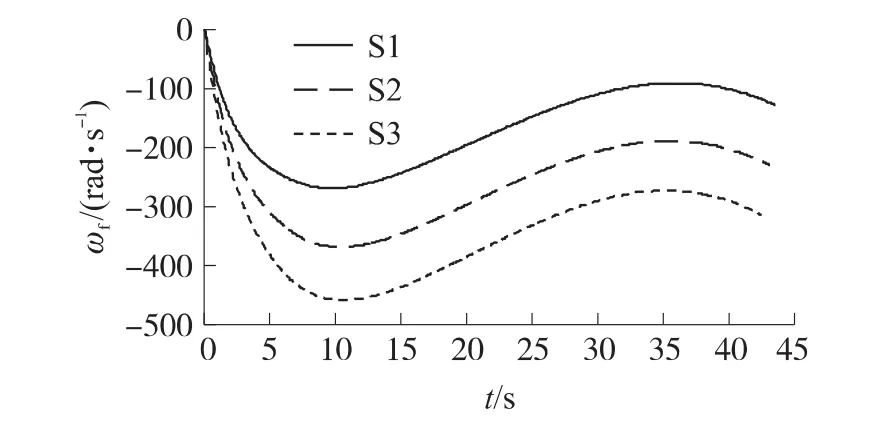
图3 不同面积下修正组件滚转角速度

4.2 相同舵片面积、不同舵偏角时仿真分析

取舵片面积相同，舵偏角分别为2°、3°、4°、5°，仿真结果见表3。

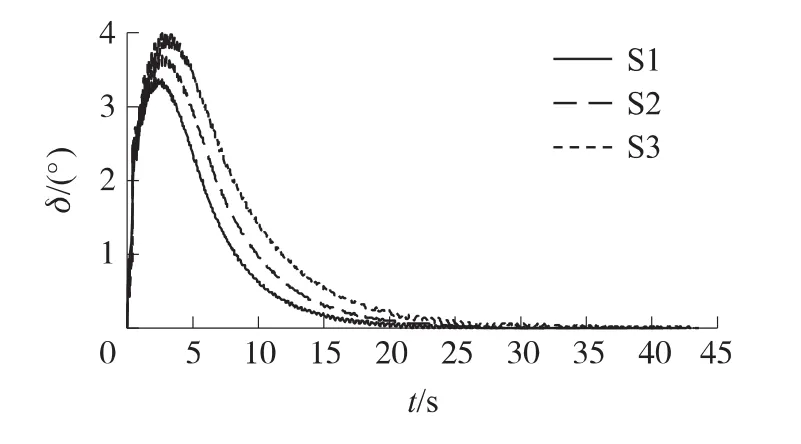
图4 不同面积下弹丸章动角

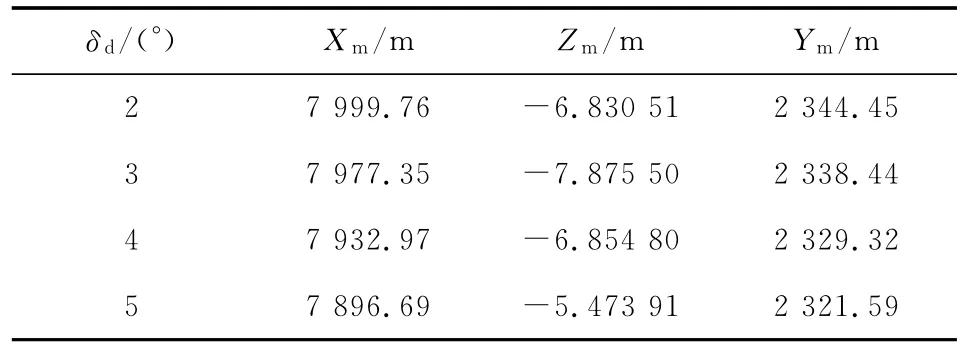
表3 相同舵偏角、不同舵片面积时弹道特征值

随舵偏角的增大，弹丸飞行过程中所受阻力、升力都将增大。对该型弹丸阻力及其射程影响较大，故随舵偏角增大，弹丸射程减小。

随舵偏角的增大，轴向力矩系数和法向力矩系数变化不大，而侧向力矩系数变化较为明显，呈线性减小趋势。但由于修正组件极转动惯量较小，其滚转角速度增大较为明显，如图5所示。随舵偏角增大，在来流作用下舵面形成的翻转力矩使弹丸的恢复力矩减小，故弹丸的章动角增大，如图6所示。

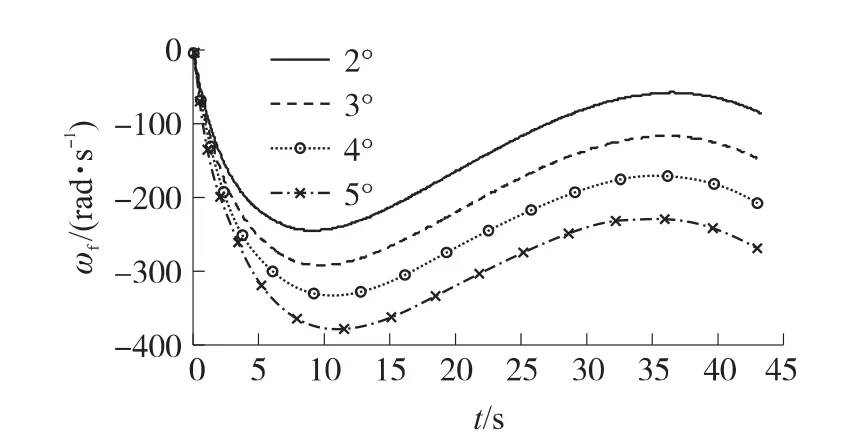
图5 不同舵偏角下修正组件滚转角速度

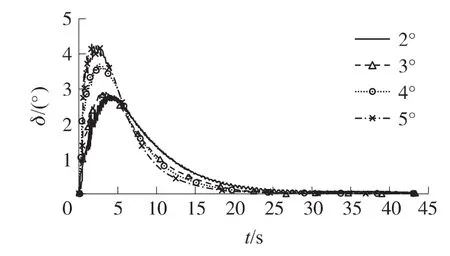
图6 不同舵偏角下弹丸章动角

4.3 不同修正组件质量时仿真分析

定义R为修正组件质量与弹丸质量的比值，无量纲。在弹丸气动外形不发生变化的条件下，表4为不同R值时弹丸的射程、侧偏和最大弹道高，图7和图8为不同R值下修正组件滚转角速度曲线和弹丸章动角曲线。

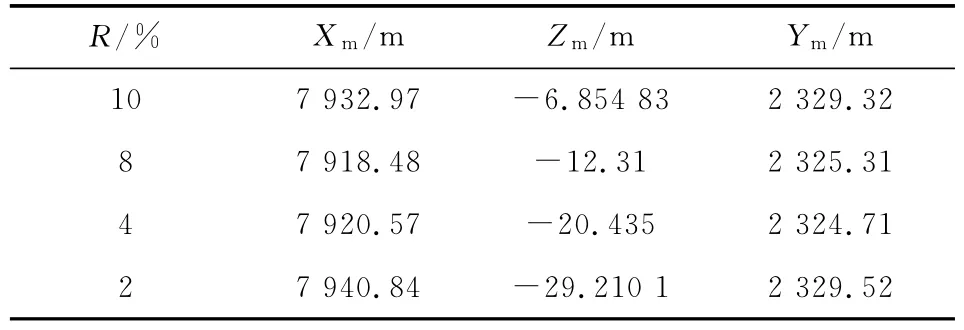
表4 不同R值时弹道特征值

由表4可知，不同R下弹丸的弹道射程、侧偏和最大弹道高变化很小。

修正组件的质量直接影响其极转动惯量，决定其滚转角加速度。质量越小，极转动惯量越小，滚转角加速度越大，修正组件越容易在导转力矩作用下滚转，如图7所示。舵片滚转整周期合力为0，故滚转角速度越大舵片受力对弹丸的影响越小，因而弹丸章动角相对较小；随着修正组件质量的增大，其极转动惯量增大，修正组件上作用的气动力矩对其影响就会相对减小，弹丸的章动角会逐渐减小，如图8所示。

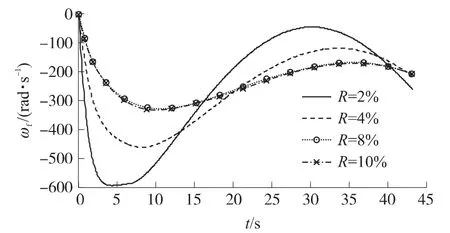
图7 不同R值下修正组件滚转角速度

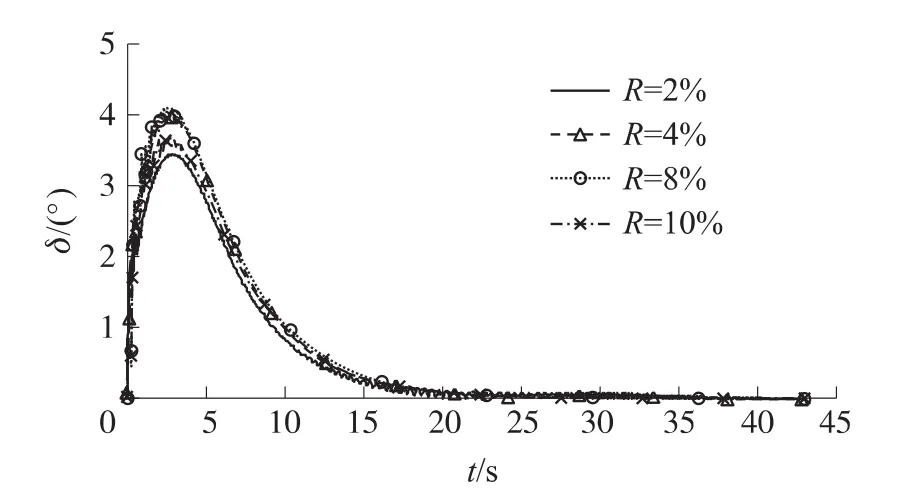
图8 不同R值下弹丸章动角

5 结束语

本文基于修正组件和弹体不存在气动耦合的假设，将弹丸作为2个刚体进行研究；分析了弹丸在飞行过程中所受的空气动力和两刚体间的相互作用，建立了7D弹道模型。针对某型尾翼稳定弹，建立了仿真模型，并对不同面积、不同舵偏角和不同修正组件质量3种状态进行了仿真分析，有效验证了模型的正确性。该模型可用于该类弹箭的弹道解算，且可为该类弹箭的研究提供参考。

［1］曾耀华.火箭弹摆动头锥弹道修正引信技术研究［D］.太原：中北大学，2010.ZENG Yao－hua.The research on swing fuse trajectory correction technology for low spin rocket missile［D］.Taiyuan：North University of China，2010.（in Chinese）

［2］王朋飞，曹红松，刘务平，等.引信头锥摆动角对火箭弹气动特性及控制能力影响［J］.弹箭与制导学报，2013，33（1）：152－155.WANG Peng－fei，CAO Hong－song，LIU Wu－ping，et al.The influence of fuse nose’s swing angle on rocket aerodynamic characteristics and control ability［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2013，33（1）：152－155.（in Chinese）

［3］CLANCY J A，BYBEE T D，FRIDRIH W.Fixed canard 2－D guidance of artillery projectile：US：6981672B2［P］.2006－01－03.

［4］马宝华.网络技术时代的引信［J］.探测与控制学报，2006，28（6）：1－5.MA Bao－hua.Fuse in networked technology era［J］.Journal of Detection ＆Control，2006，28（6）：1－5.（in Chinese）

［5］COSTELLO M.Modeling and simulation of a differential roll projectile［C］／／Modeling and Simulation Technologies Conference.Boston：AIAA，1998：490－499.

［6］郝永平，孟庆宇，张嘉易.固定翼二维弹道修正弹气动特性分析［J］.弹箭与制导学报，2012，32（3）：171－173.HAO Yong－ping，MENG Qing－yu，ZHANG Jia－yi.Aerodynamic characteristic analysison two－dimensional trajectory corrector shell with fixed－wing［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2012，32（3）：171－173.（in Chinese）

［7］张嘉易，王广，郝永平.二维弹道修正弹鸭舵修正机构气动特性研究［J］.弹箭与制导学报，2013，33（2）：88－91.ZHANG Jia－yi，WANG Guang，HAO Yong－ping.Investigation of aerodynamic characteristics for two－dimensional trajectory correction projectile canard rudder device［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2013，33（2）：88－91.（in Chinese）

［8］纪秀玲，王海鹏，曾时明.可旋转鸭舵对旋转弹丸纵向气动特性的影响［J］.北京理工大学学报，2011，31（3）：265－268.JI Xiu－ling，WANG Hai－peng，ZENG Shi－ming.CFD prediction of longitudinal aerodynamic for a spinning projectile with fixed canard［J］.Transactions of Beijing Institute of Technology，2011，31（3）：265－268.（in Chinese）

［9］WERNERT P.Stability analysis for canard guided dual－spin stabilized projectiles［C］／／Atmospheric Flight Mechanics Conference.Chicago：AIAA，2009：1－24.