压电舵翼动力学模型研究

周玉华，周长省，陈 雄

（南京理工大学 机械工程学院，南京210094）

智能弹药系统（IMS）是要整合进未来战斗系统共同作战环境的系统之一，特别是一些能同时执行飞行巡逻和攻击的微小型智能弹药，因其使用方便，成本低，隐蔽性好等优点而备受关注，作为飞行控制的舵翼结构是这类系统的重要组成部分［1－2］。在微机电驱动技术中，压电驱动器由于结构简单，兼容性好而被广泛应用。许多学者尝试将压电驱动器应用在舵翼驱动上［3－9］。对于压电舵翼的动力学性能研究，目前主要是通过实验测量。本文针对一种压电舵翼结构，建立了其动力学模型，为压电驱动器的动力学特性研究提供了理论依据。

1 压电舵翼结构与工作原理

压电舵翼结构如图1所示，压电舵翼总体由三部分组成：固定支架、压电双晶片驱动器以及襟翼。固定支架为压电双晶片驱动器和襟翼提供了固定与运行的平台，同时也是将舵翼系统固定于机身的部件；压电双晶片驱动器是该系统的运行动力源，使舵翼按照控制实现偏转；襟翼在驱动器的作用下发生偏转，其气动特性发生变化，从而实现对飞行的控制。固定支架前部有一个卡槽，用来固定压电双晶片驱动器。后面有一对支座通过转轴连接襟翼。固定支架与后面的襟翼形成一个铰链结构。压电驱动器的自由端通过一个滑槽驱动器襟翼双向偏转。整个舵翼系统的工作原理是固定支架将系统安装于机身之上，压电双晶片驱动器左端固定在支架前部的卡槽内，另一端再装配在襟翼的滑槽内。当对压电双晶片驱动器施加电压时，驱动器发生弯曲变形，自由端产生横向位移，通过滑槽拨动后面襟翼绕转轴偏转。

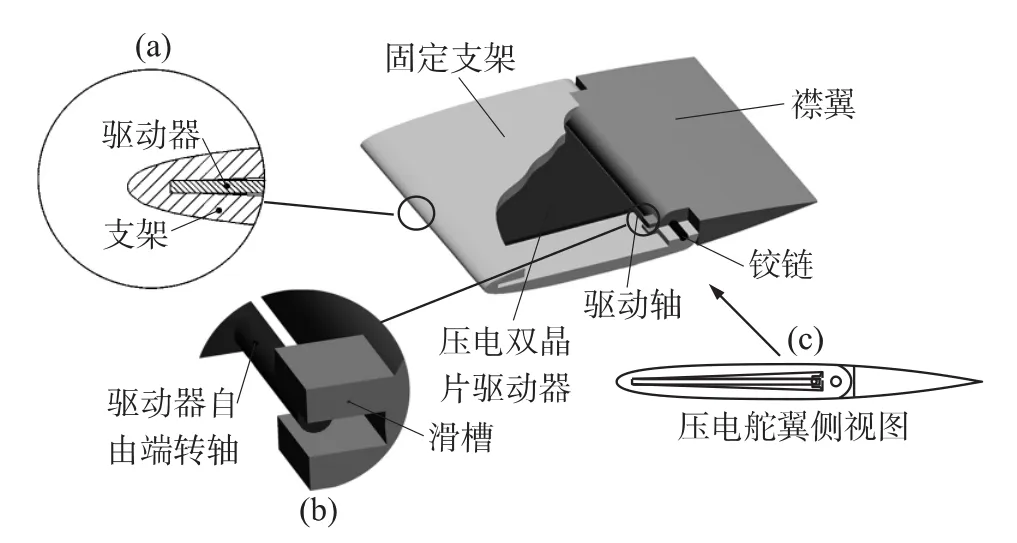
图1 压电舵翼结构示意图

舵翼整体尺寸为80mm×40mm×8mm，压电驱动器尺寸40mm×30mm×1.1mm，除去固定部分长度，实际运动部分长度约为38mm，驱动轴到襟翼转轴之间的距离应该为4.59mm。

动力学模型中涉及的材料参数主要有压电陶瓷密度7 600kg／mm，铜基底密度8 900kg／mm，压电陶瓷短路条件下的方向弹性模量为59.8GPa，铜弹性模量为115GPa。

2 压电舵翼动力学模型

由前面对压电舵翼结构和工作原理的表述可知，该结构可用图2表示其工作原理。压电双晶片驱动器一端固定，一端自由，属于典型的悬臂梁结构，而在驱动器工作过程中所受的所有外载荷均是通过襟翼上的滑槽施加在压电双晶片驱动器的自由端。

图2 压电舵翼原理图

建立模型时，可以认为结构中任一单元的横向平动动能远大于该单元的转动动能。对单元的转动动能予以忽略。基于以上能量方面的结论，则可以进一步认为结构任一单元的弯曲变形所引起的势能变化远大于剪切变形所引起的势能变化，从而忽略结构变形时的剪切变形。

驱动器弯曲变形如图3所示，图中Q为横截面剪应力，M为横截面弯矩，q为分布载荷。这里以挠曲线为对象以描述结构的振动，设变形后的挠曲线为

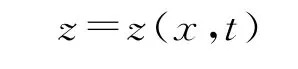
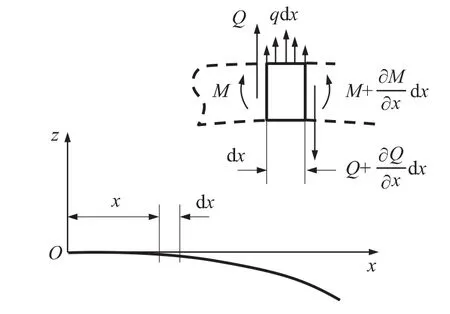
图3 驱动器弯曲变形示意图

为了说明普遍情况下的结构振动状态，这里分析分布载荷下结构的动力学响应。沿长度方向上在压电驱动器上取长度为dx的单元进行分析。单元所受分布载荷以及左右2个横截面剪应力和弯矩的情况如图3所示。这里按材料力学中的规定，认为使单元向下凹的弯矩为正。由单元的受力情况，根据力和转矩的平衡方程可得：

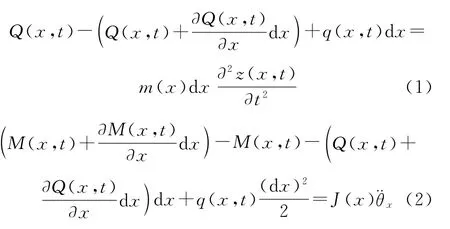
式中：m（x）为结构的面密度，即单位长度的质量；J为单元的转动惯量；θx为单元转角。由本节开始的假设，在研究动力学特性时，单元的转动分量是忽略的，因此式（2）右端可以认为是0。对上述两方程化简，略去高阶微分项可得：

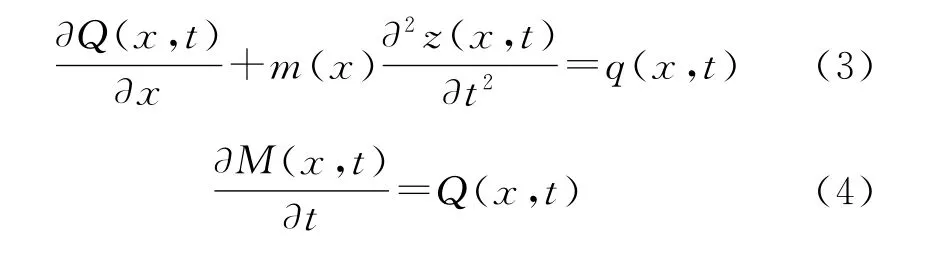
材料力学中，弯矩与变形存在如下关系：

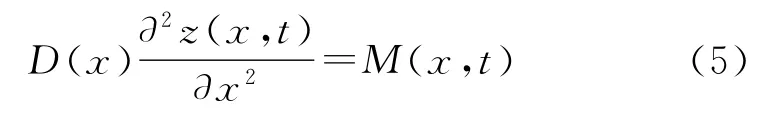
式中：D（x）为截面的抗弯模量。联立式（3）～式（5），可得：

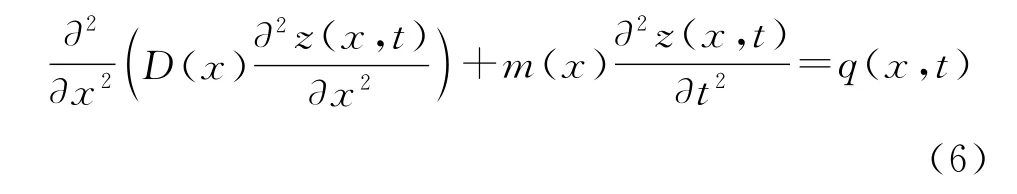
自由振动情况下，同时假设结构的横截面保持不变，则式（6）中的D（x）和m（x）为恒定值，从而方程可以写成：

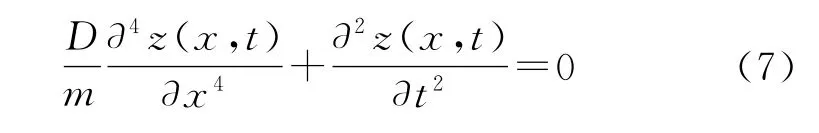
根据振动学“同步运动”理论，结构上各点在振动时，位移随时间的变化可以分解成两部分，即：

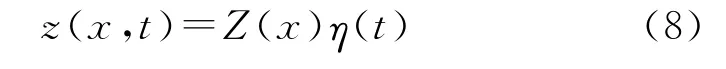
式中：Z（x）为振型函数，它表示整个结构振动时的空间形状，是与时间无关的；η（t）为振动函数，它表示振动随时间的变化规律。将式（8）代入式（7）中，并在所得方程两边同除以z（x，t），可得：

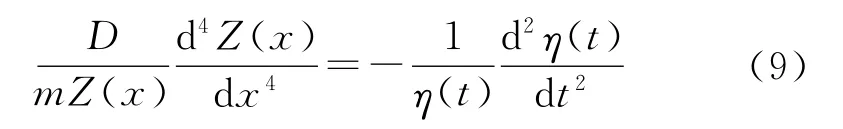
式（9）的左端为x的微分项，而右端为t的微分项，若要两边相等则必定左右两端等于常数，设这个常数为ω2，则式（9）可以分开写成2个等式：

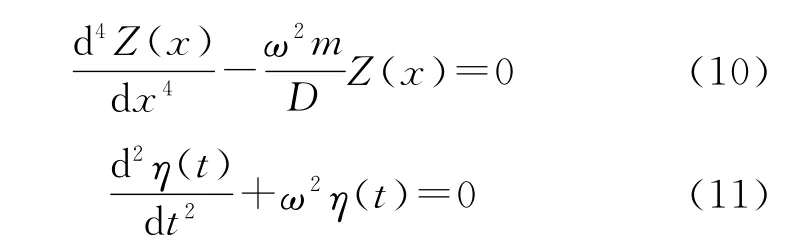
上述两方程的通解可以写为

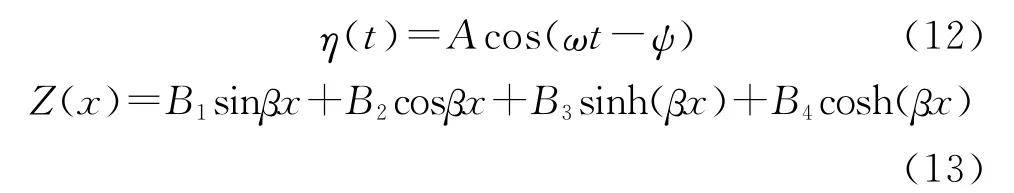
由于外载荷全部通过襟翼滑槽作用在驱动器自由端，则可以认为驱动器的边界条件为左端固定，右端受到集中载荷的作用。因此，压电舵翼工作时，驱动器左端边界条件可以表示为

F为驱动器自由端所受载荷。由边界条件（14）可得：

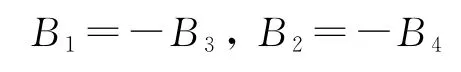
则式（13）可以写为

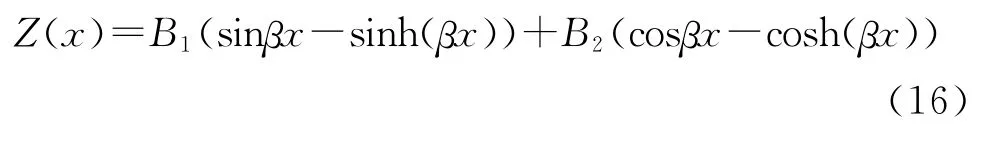
再由边界条件（15），有：

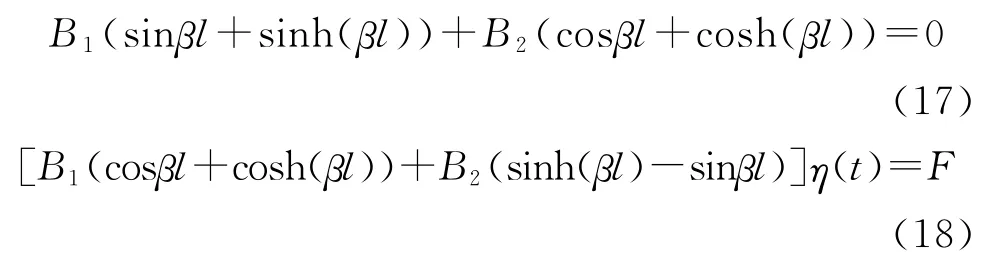
压电驱动器自由端的集中力必定与自由端的运动相关，根据式（8）可知，自由端的运动可以表示为

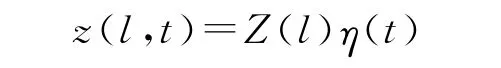
若将集中力看作为一个等效的集中质量块作用在压电双晶片驱动器自由端，则集中力可以表示为

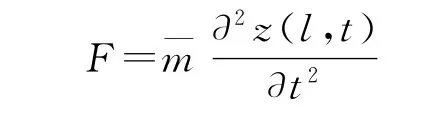
式中：为等效集中质量。则式（17）可以写为

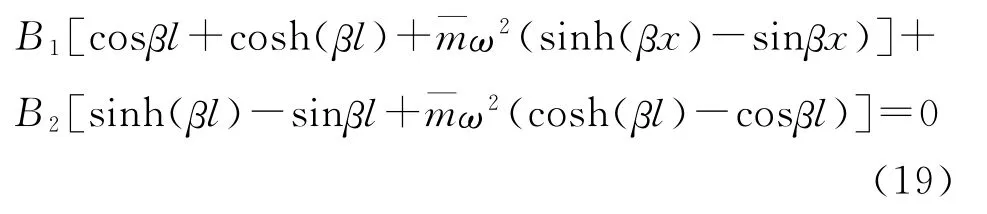
同样，方程组需要满足行列式：

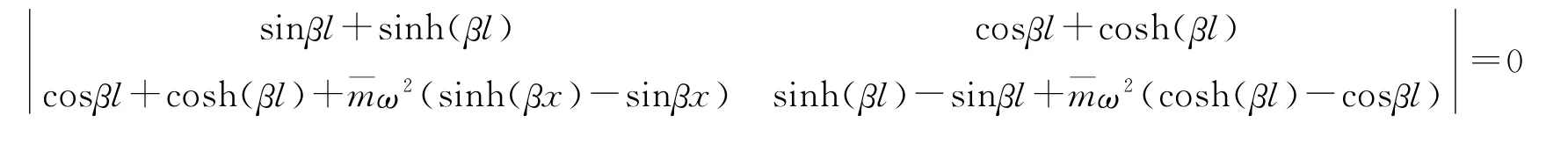
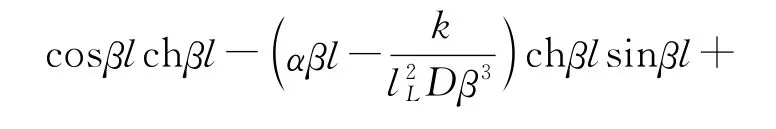
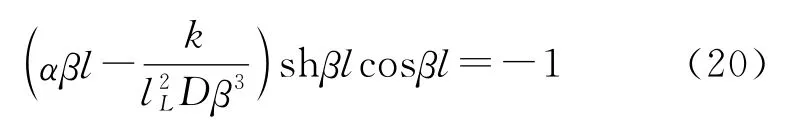
等效集中质量是由压电双晶片驱动器自由端所受的集中载荷决定的，通过分析可知，产生集中载荷的因素主要来源于两个方面：襟翼自身转动惯性以及飞行过程中作用在襟翼上的空气动力所产生的铰链力矩。这个铰链力矩可以表示为

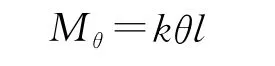
式中：k为比例系数，由舵翼的尺寸、翼型、飞行条件等决定；θ为攻角；l为气动中心到襟翼转轴的距离。根据上式可知，对于确定舵翼结构的翼型和尺寸，l为固定不变的。舵翼所受气动力的大小主要由飞行速度以及舵翼的攻角所决定。舵翼的翼型与尺寸是由飞行器的飞行要求以及飞行器质量决定的。根据这两点可以推论，作用在襟翼上空气动力的大小其实是由飞行器的飞行要求以及飞行器的质量决定的。微型飞行器的飞行是相对平稳的，同时对于尺寸比较小的微型飞行器，其质量必然也是较小的。通过以上分析可知，作用在襟翼上的空气动力是一个变化不剧烈、不太大的力。由于空气动力的不确定，这里主要分析襟翼自身惯性的影响。

襟翼通过转轴固定在前面的固定支架上，舵翼运作时，襟翼作绕转轴的定轴转动，因此对襟翼有：

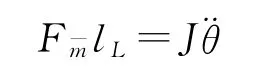
式中：F¯m为襟翼与驱动器自由端之间的作用力，J为襟翼相对于转轴的转动惯量。上式可以变形为

襟翼外形是不规则的，人工计算其转动惯量比较困难。因此，为了简单快捷地得到襟翼的转动惯量，这里用Pro／Engineer软件对襟翼进行三维建模，尼龙材料的比重为1.15，软件计算绕模型坐标系z轴的转动惯量为J33＝6.869 5×10－1。襟翼工作时并不是以质心为中心转动，而是绕转轴作定轴转动。襟翼绕转轴的转动惯量可以用移轴公式计算。软件计算襟翼的质量为9.236g，质心坐标为（18.783 5，0，0），而模型中转轴的坐标为8.37。利用移轴公式可以计算出襟翼绕转轴的转动惯量：

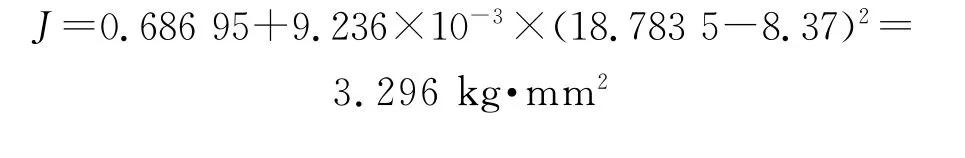
由式（21）中等效集中质量的表达式以及lL的设计值，可以得到襟翼的等效质量为

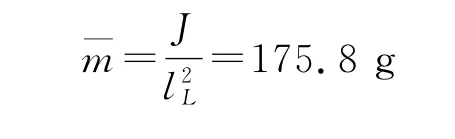
这里主要考虑襟翼的转动惯量对舵翼系统动态性能的影响。将参数α代入式（20），并用数值法解之可得压电舵翼系统的一阶频率的特征值为βl＝0.673 4。代入方程中，可得：

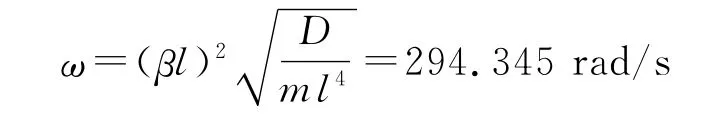
根据频率关系ω＝2πf，可以计算出压电舵翼的一阶频率为46.85Hz。

3 压电舵翼动力学响应测量与动力学参数计算

根据信号分析的理论可知，时域中的阶跃跳变信号在频域中包含了无限的频率分量。因此，用阶跃信号对系统进行激励时，相当于用各种不同频率的信号激励系统。同时阶跃信号也是系统运行遇到的最多的输入激励。

对于压电舵翼系统动态性能的测量，这里考虑转化为使用应变片测量压电双晶片驱动器陶瓷片的应变来实现，由于系统装配后尺寸小，结构紧凑，因此粘贴应变片的工作必须在压电舵翼系统装配之前完成。

应变片由于应变而产生的阻值变化通过电桥转变为电信号，该信号经过电阻应变仪的滤波、放大等处理后用美国Tektronix公司生产的TDS3000C型数字示波器进行采集记录。实验结束后，通过示波器自身的USB接口，将所得数据存储在电脑中。实验系统实物如图4所示。

图4 舵翼动态试验系统

对系统施加250V阶跃信号，舵翼系统的响应如图4所示。由图可知，舵翼系统在阶跃信号作用下存在一个明显的振荡过程，然后很快到达平衡状态。由振动学理论可知，舵翼系统在阶跃信号激励下调整至稳定状态之前的振荡频率称为有阻尼自振角频率。图5为压电舵翼阶跃响应，图中U为测量信号。由图5可知，舵翼系统的有阻尼自振周期约为23ms，超调约为15%。

根据控制工程理论，系统响应的峰值时间为

前文已经求得系统无阻尼频率ωn＝294.345rad／s。由舵翼系统的阶跃响应曲线可以测量得到峰值时间为tp＝13ms。将ωn，tp代入式（22）中可以得到压电舵翼系统的阻尼比为ξ＝0.571 5。阻尼比的计算结果验证了舵翼系统在阶跃信号作用下的欠阻尼响应。

另一方面，根据理论计算得到系统无阻尼自振角频率ωn＝294.345rad／s，阻尼比ξ＝0.571 5，可以代入公式：

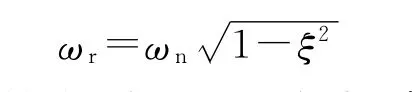
计算舵翼系统的有阻尼自振角频率为ωr＝241.54rad／s，代入公式：

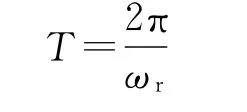
可以得到舵翼系统的理论有阻尼自振周期T＝26ms，这与实验测量得到的23ms接近，验证了所建立的压电舵翼系统动态模型的正确性。

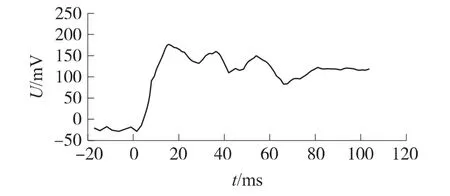
图5 压电舵翼阶跃响应

4 结束语

本文建立了一种压电舵翼的动力学模型，揭示了这种结构压电舵翼是二阶系统的动力学本质。再结合该动力学模型，通过测量舵翼系统在阶跃信号激励下的动态响应，得到系统的动力学参数，为舵翼的结构优化以及控制奠定了基础。

［1］BARRETT R，GROSS R S，BROZOSKI F.Missile flight control using active flexspar actuators［J］.Smart Materials and Structures，1996，5（2）：121.

［2］BARRETT R，VOS R.Design，development and testing of a transonic missile fin employing PBP／DEAS actuators［C］／／The 15th International Symposium on：Smart Structures and Materials ＆Nondestructive Evaluation and Health Monitoring.California，USA：International Society for Optics and Photonics，2008：693011－693011－11.

［3］ROGET B，CHOPRA I.Wind－tunnel testing of rotor with individually controlled trailing－edge flaps for vibration reduction［J］.Journal of Aircraft，2008，45（3）：868－879.

［4］STRAUB F K，KENNEDY D K，DOMZALSKI D B，et al.Smart material－actuated rotor technology–SMART［J］.Journal of Intelligent Material Systems and Structures，2004，15（4）：249－260.

［5］DIETERICH O，ENENKL B，ROTH D.Trailing edge flaps for active rotor control－aeroelastic characteristics of the ADASYS rotor system［C］／／Annual Forum Proceedings－American Helicopter Society.Phoenix，USA：American Helicopter Society，INC，2006，62（2）：965.

［6］J¨ANKER P，HERMLE F，FRIEDL S，et al.Advanced piezoelectric servo flap system for rotor active control［C］／／32nd European Rotorcraft Forum.Moscow：Russian Helicopter，JSC，2006：237－247.

［7］GLAZ B，FRIEDMANN P P，LIU L.Vibration reduction and performance enhancement of helicopter rotors using an active／passive approach［C］／／Proceedings of the 49th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference.Schaumburg， IL， USA： AIAA，2008：338－350.

［8］GIURGIUTIU V.Review of smart－materials actuation solutions for aeroelastic and vibration control［J］.Journal of Intelligent Material Systems and Structures 2000，11：525–44.

［9］ROTH D，ENENKL B，DIETERICH O.Active rotor control by flaps for vibration reduction—full scale demonstrator and first flight test results［C］／／32nd European Rotorcraft Forum.Moscow：Russian Helicopter，JSC，2006：801－814.