有摩擦的美式未定权益的上套期保值价格分析＊

沈建平，唐矛宁

（湖州师范学院 理学院，浙江 湖州313000）

0 引 言

美式未定权益问题研究由来已久，Mckean［1］很早就较深入地分析了美式期权，并把未定权益的定价问题转换为自由边界问题，把美式期权的价格同最优停止边界联系起来.Bensoussan［2］和Karatzas［3］分别在1984年和1988年研究了完备的无摩擦金融市场中的美式未定权益定价问题，用套期保值和等价鞅测度理论得到了完备市场下的标准定价理论.1998年，Karatzas和Kou［4］对投资策略受限制的美式未定权益定价问题进行了研究，用Doob－Meyer分解和随机控制方法解决了投资策略受限制的美式未定权益的套期保值问题.

本文主要研究的也是有摩擦金融市场中美式未定权益的套期保值问题，新颖之处在于所讨论的金融市场的摩擦性同时表现在三个方面：一是投资策略受限制；二是借款利率大于存款利率；三是投资者拥有或借入某种股票需交纳比例费用.参考文献［3～8］中的证明方法，通过引入反映上述金融市场摩擦的辅助无摩擦金融市场类，使用鞅表示定理和一致Doob－Meyer分解给出了美式未定权益的上套期保值价格hup（K）的定价公式，并证明了最优上套期保值策略的存在性.本研究与文献［8］相比较，考虑的问题更一般，更具有现实意义.

1 基本模型

设金融市场M中有d＋1种标的资产：一种是无风险资产；另外d种是风险资产.用P0（t）表示无风险资产在t时刻的价格，且在［0，T］内满足：

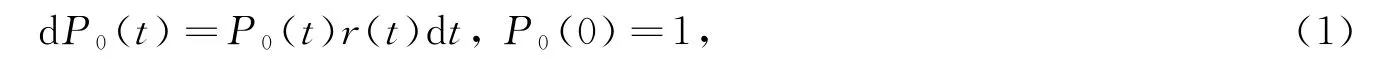
其中：r（t）为时刻t的短期存款利率；Pi（t）为第i种股票在t时刻的价格（i＝1，2，…，d），且在［0，T］内满足：

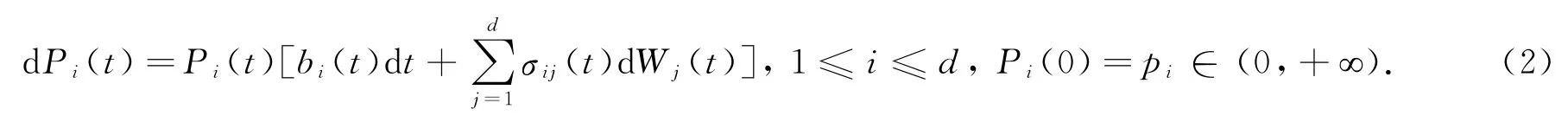
在（2）式中，W（t）＝（W1（t），…，Wd（t））＊，0≤t≤T（＊表示向量的转置），为带域流的完全概率空间（Ω，F，（Ft）0≤t≤T，P）上的一个d维标准布朗运动.其中：（Ft）0≤t≤T为布朗运动W（·）生成的自然σ－域流的扩张；σij（·）为股票价格的波动系数；bi（·）为股票的平均回报率；pi＞0是第i种股票的初始价格.记b（t）＝（b1（t），…，bd（t））＊，σ（t）＝（σij（t））d×d，0≤t≤T.

设b（t），r（t），σ（t），0≤t≤T满足假设H1：过程b（·），r（·），σ（·）为［0，T］×Ω上的（Ft）0≤t≤T循序可测过程；过程b（·），r（·），σ（·）在［0，T］×Ω是一致有界的；对∀（t，ω）∈［0，T］×Ω，矩阵σ（t，ω）的逆σ－1（t，ω）存在，且在［0，T］×Ω 是一致有界的.

2 财富方程

定义1 一个（Ft）0≤t≤T循序可测过程π：［0，T］×Ω →Rd称为一个投资策略，如果＜＋∞，a.e..

定义2 一个（Ft）0≤t≤T循序可测过程C：［0，T］×Ω→［0，＋∞）称为消费过程，如果C（0）＝0，C（T）＜∞，a.e.，且它的轨道是右连左极递增的.

但在实际金融市场中，存款利率和借款利率常常是不一样的，且借款利率常大于存款利率.设t时刻借款利率为R（t），且满足假设H2：R（·）是［0，T］×Ω上的（Ft）0≤t≤T循序可测过程；R（t，ω）≥r（t，ω），a.e.（t，ω）∈［0，T］×Ω；R（·）在［0，T］×Ω上一致有界.特别地，如果R（t，ω）＝r（t，ω），a.e.（t，ω）∈［0，T］×Ω，称为金融市场无摩擦.

另外，设在金融市场中投资有管理费要求：投资者借入第i种股票需缴纳的管理费比例为1＞ni≥0，i＝1，…，d；持有第i种股票需缴纳的管理费比例为1＞mi≥0.

对初始财富x≥0，任何一对投资消费策略（π，C），其所对应的财富过程Xx，π，C满足随机微分方程：

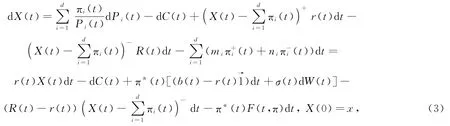
其中：Fi（t，π）＝miI｛ πi（t）≥0｝－niI｛πi（t）＜0｝；F（t，π）＝（F1（t，π），…，Fd（t，π））＊.其解X（·）称为初始财富x和投资消费策略（π，C）所对应的财富过程Xx，π，C.

定义3 一对投资消费策略（π，C）关于初始财富x≥0为可允许的，如果Xx，π，C（t）≥0a.e.，∀0≤t≤T.Α0（x）表示关于初始财富x的可允许投资消费策略（π，C）的全体.

3 凸投资策略

实际金融市场中的投资策略总是受到一定的限制.这种限制主要来自两个方面：一是金融市场监督者为防止投资者特别是大投资者操纵市场而强制规定的一些限制条件；二是投资者本身为防范风险也会做出一些投资策略限制.下面给出投资策略受到限制的情况下的一种数学模型.

设K＋和K－是Rd上的两个凸闭集，K＋∩K－非空，K＋包含原点.

对可允许投资的消费策略作如下限制：A（x）｛（π，C）∈A0（x）在｛Xx，π，C（t）≥0｝上，ρ（t）∈K＋；在｛Xx，π，C（t）≤0｝上，ρ（t）∈K－，∀0≤t≤T｝.其中ρ（·）为投资比例.

这种可允许投资消费策略取值于A0（x）的市场模型M记作M（K）.

下面讨论在本文中起重要作用的－K的支撑函数.

设－K的支撑函数是δ（x），且

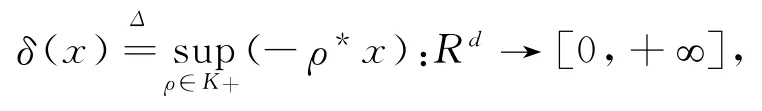
其有效定义域为：

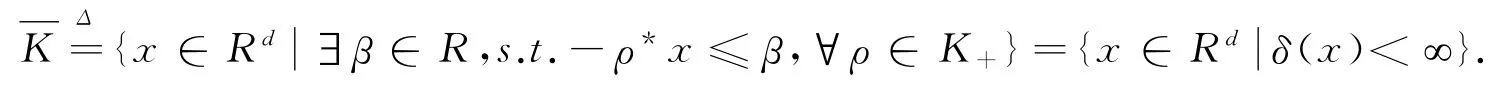
由凸分析的知识易知，支撑函数δ（x）为闭的正齐次正常凸函数［9］.本文还假设δ（·）在上是连续的.

4 美式未定权益的上套期保值价格

定义4 美式未定权益定义为一个非负随机过程B：［0，T］×Ω→［0，＋∞），它是（Ft）0≤t≤T－适应过程，具有连续轨道，且存在实数ε＞1，使得

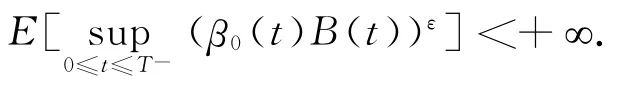
美式未定权益B在市场M（K）中的上套期保值价格定义为：

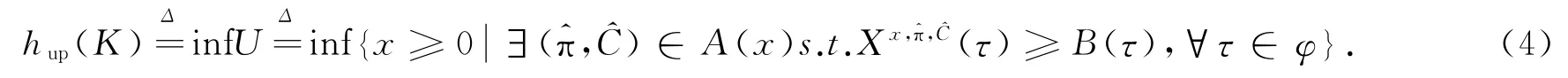
本文通过引入反映市场摩擦的辅助无摩擦金融市场类，使用随机控制和随机分析的工具对金融市场M（K）中的美式未定权益B的上套期价格分别进行刻画.

下面首先引入辅助无摩擦金融市场.D｛（ν，μ，γ）ν，μ均为d－维循序可测过程，且－mi≤νi≤ni，∀1≤i≤d；0≥μ1＝μ2＝…＝μd≥－（R－r）ae..［0，T］×Ω，γ：［0，T］×Ω →K，为｛Ft｝0≤t≤T循序可测过程，且满足‖2＋δ（ν（t）））dt＜＋∞｝.

对∀（ν，μ，γ）∈D所对应的无摩擦金融市场Mν，μ，γ中有一种无风险资产和d种风险资产，其价格方程分别为：

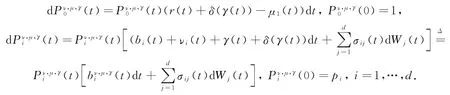
贴现因子过程为：

风险市价过程为：

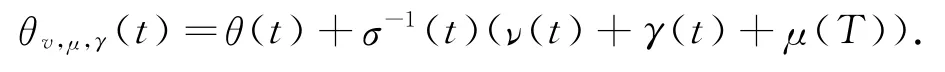
再定义：

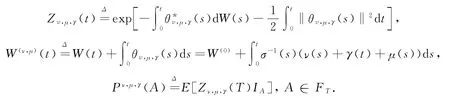
由Girsanov定理知，W（ν，μ，γ）（·）在概率测度Pν，μ，γ下为标准布朗运动.对∀（ν，μ，γ）∈D定义

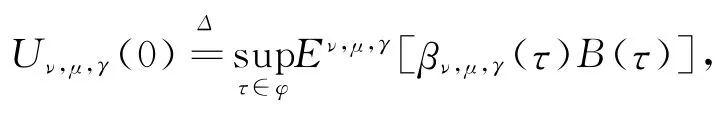
其中：Eν，μ，γ为在概率测度Pν，μ，γ下求数学期望.定义

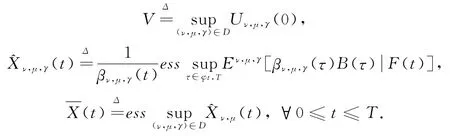
由美式未定权益定价的标准性理论知，Uν，μ，γ（0）为美式未定权益B（·）在完备的无摩擦金融市场Mν，μ，γ中的无套利价格；，μ，γ（·）为B（·）在［0，T］上的价格过程.

引理1 对于∀（ν，μ，γ）∈D，βν，μ，γ（·）（·）为Pν，μ，γ上鞅，且过程（·）具有右连左极修正.

证明可参考文献［4］～［6］中的方法.

定理1 在投资存在管理费的高借款利率下的金融市场M（K）中，美式未定权益B（·）的上套期保值价格为：

如果V＜∞，则存在投资消费策略，使得XV，＾π，Ĉ（τ）＝（τ）≥B（τ），∀τ∈φ.即是未定权益B（·）的最优上套期保值策略.

证明 先证hup（K）≥V.如果hup（K）＝∞，则不等式自然成立.若hup（K）＜＋∞，则（4）式中的集合U非空.对∀x∈U，由U的定义知存在∈A（x），使得对∀τ∈φ，Xx，＾π，Ĉ（τ）≥B（τ）.由（3）式和乘积公式得：

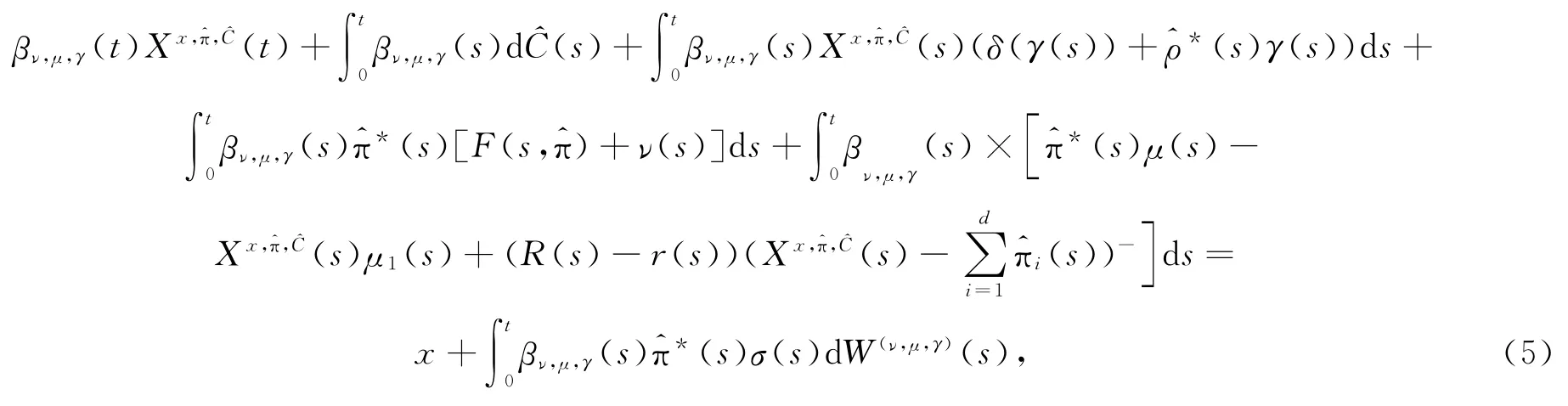
其中：

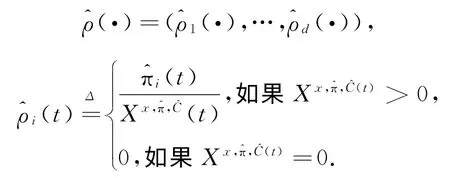
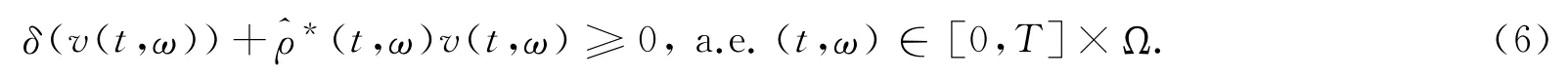
由0≥μ1＝μ2＝…＝μd≥r－R得：

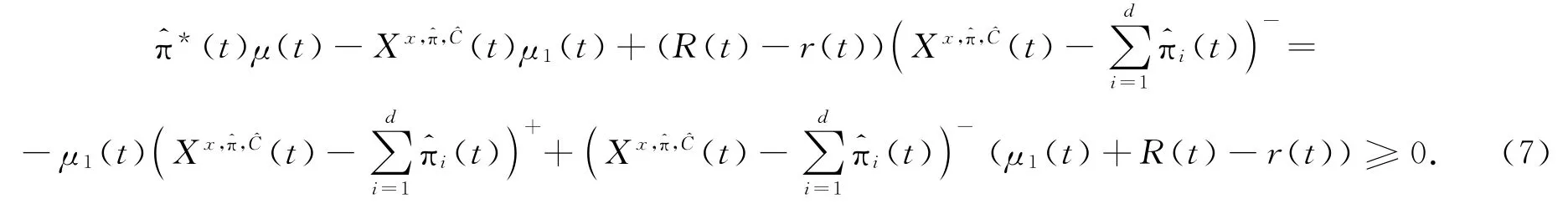
由－mi≤ν≤ni得：

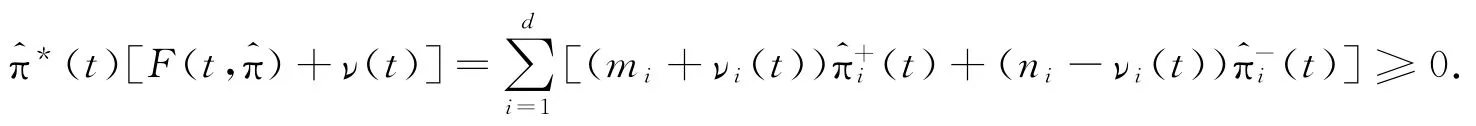
由（6）式和（7）式可知，过程（5）式是非负Pν，μ，γ局部鞅，从而为Pν，μ，γ上鞅.再由可选轨道理论知：

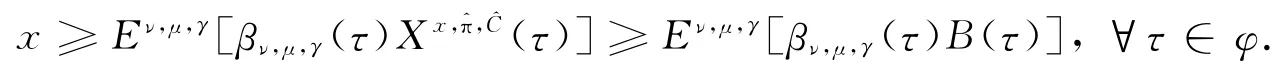
从而由x∈U，τ∈φ和（ν，μ，γ）∈D的任意性可知hup（K）≥V.

下面证明hup（K）≤V.

若V＝∞，结论显然成立.若V＜∞，由Doob－Meyer分解和鞅表示定理，可把引理1中的Pν，μ，γ上鞅βν，μ，γ（·）（·）表示为：

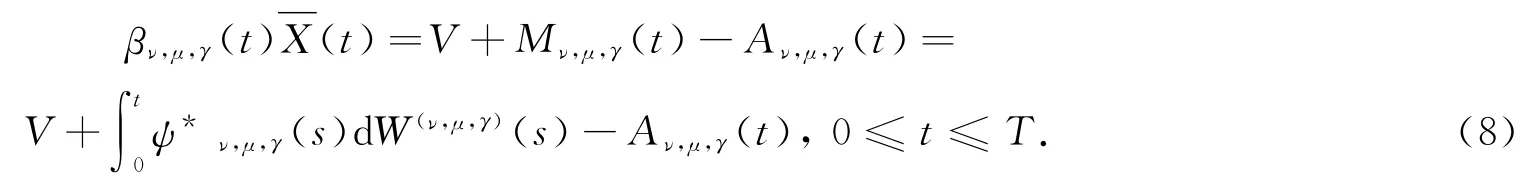
其中：ψν，μ，γ为［0，T］×Ω上取值于Rd的（Ft）0≤t≤T循序可测过程，且‖ψν，μ，γ（t）‖2dt＜∞a.e.；Aν，μ，γ为定义在［0，T］×Ω上的具有右连左极递增轨道的非负（Ft）0≤t≤T适应过程，且Aν，μ，γ（0）＝0，A（T）≤∞.

对∀（ν，μ，γ）∈D，（λ，φ，ψ）∈D，由（8）式和Itô的乘积得：

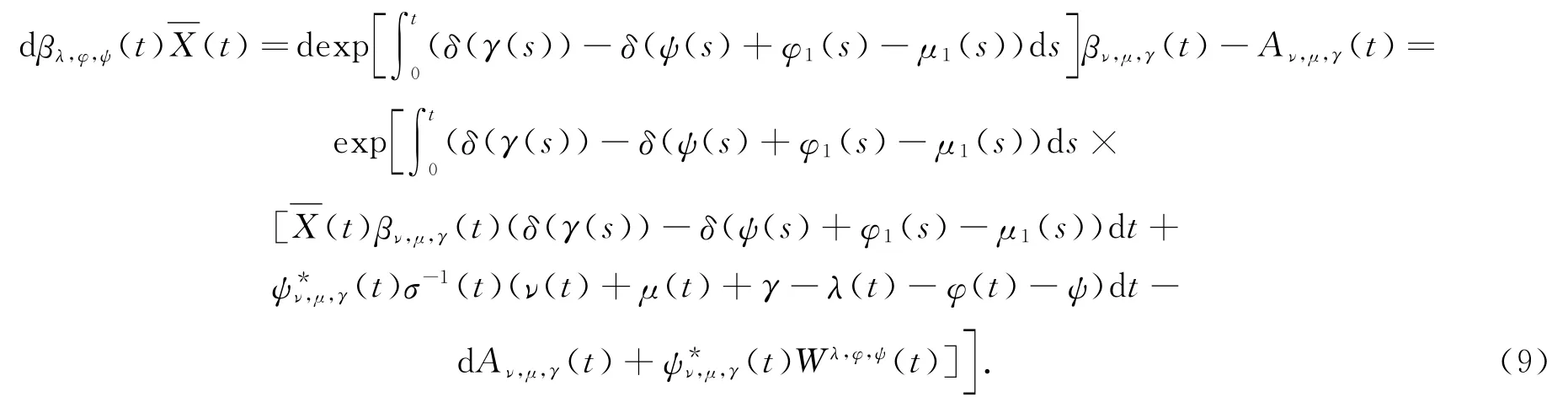
设βλ，φ，ψ（·）（·）有Doob－Meyer分解，

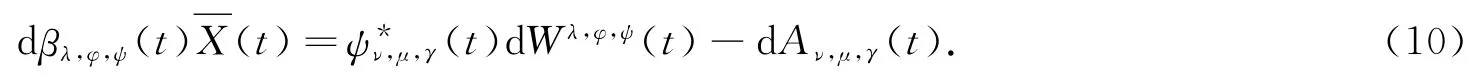
比较（9）式和（10）式得：

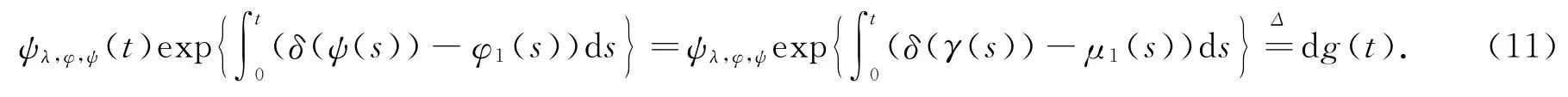
则g（t）与（ν，μ，γ）无关.定义一个取值于Rd的平方可积适应过程（·）＝（·），…（·））＊：

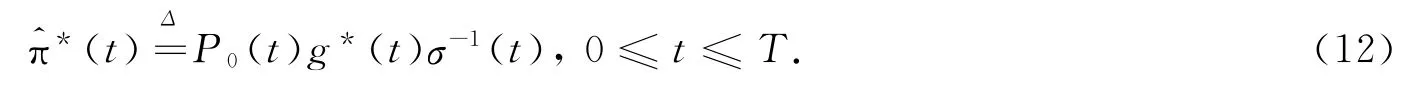
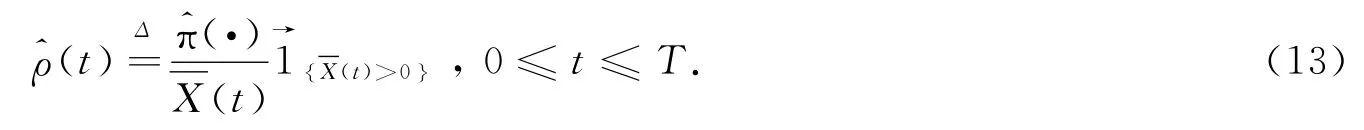
则（·）可以看作股票的投资比例.由（11）式～（13）式知，随机过程ψν，μ，γ（·）可表示为：

将（14）式代入（9）式再与（10）式比较得：

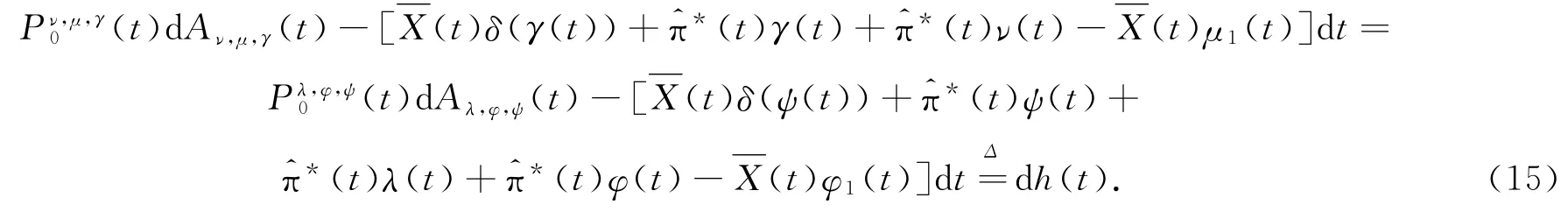
则h（t）与（ν，μ，γ）无关.再定义一个随机过程：

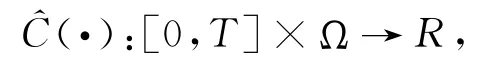
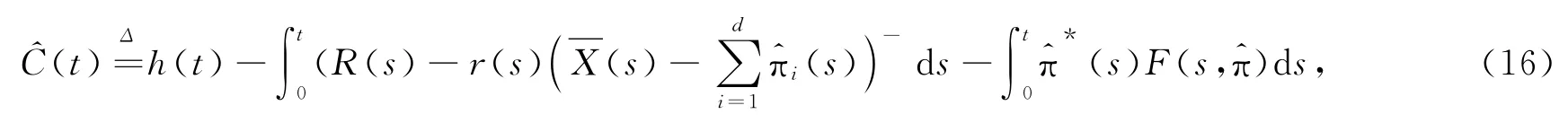
特别地取

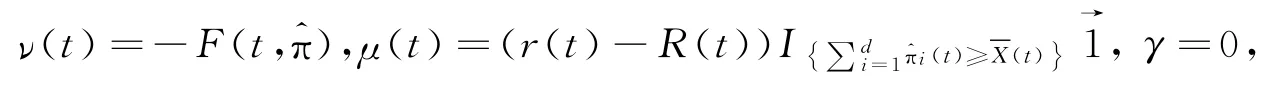
则

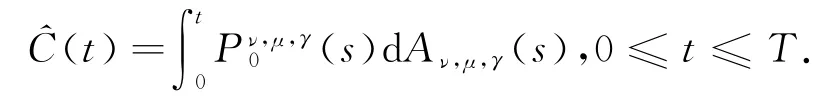
由（15）式和（16）式知，随机过程Aν，μ，γ（·）可表示为：

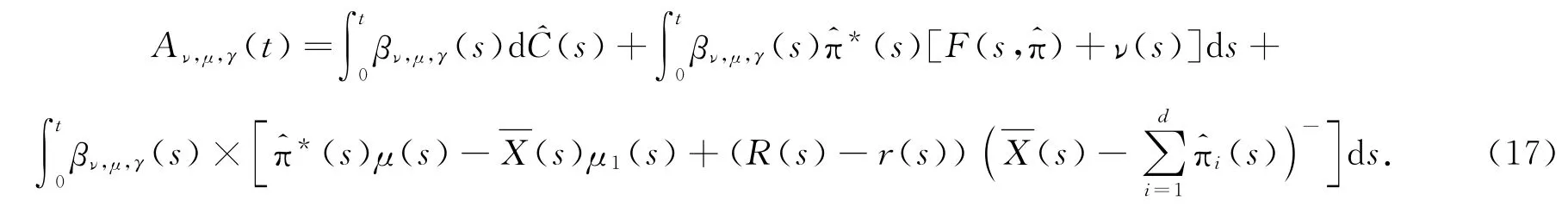
下面建立一个重要的不等式：

对∀（ν，μ，γ）∈D，

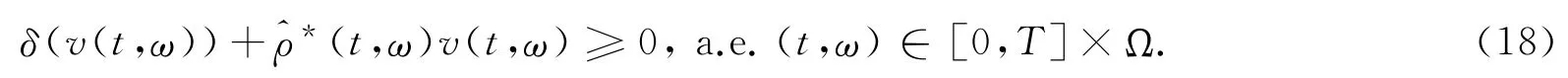
下面证明（18）式.

如果存在（ν，μ，γ）∈D，使得（18）式不成立，对∀0≤t≤T定义

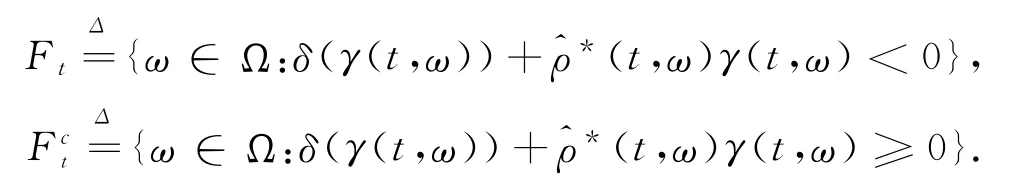
定义

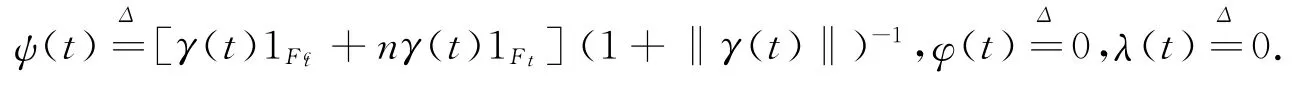
则（λ，φ，ψ）∈D取充分大的n，由（18）式和δ（x）的正齐次性知：

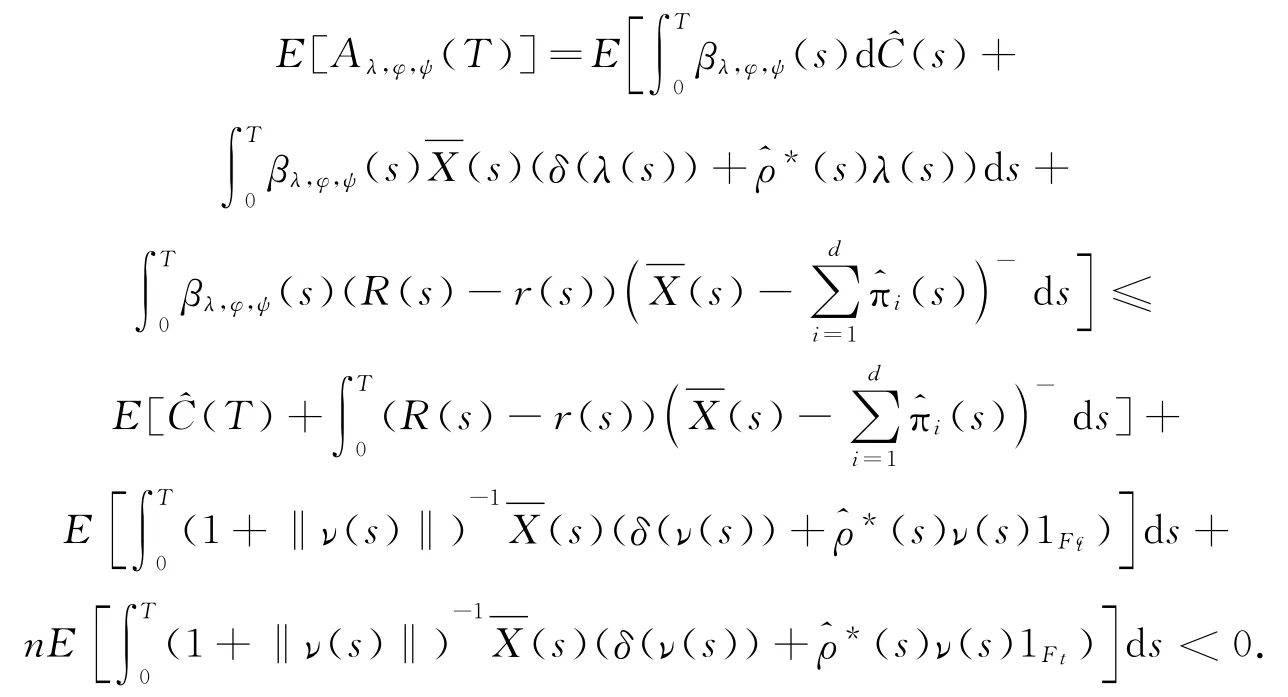
结果与E［Aλ，φ，ψ（T）］≥0矛盾，因此不等式（18）式成立.

将（14）式和（18）式代入（8）式，得：

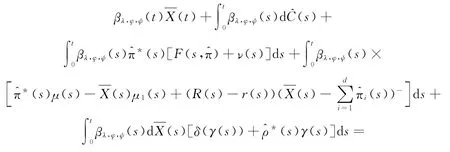
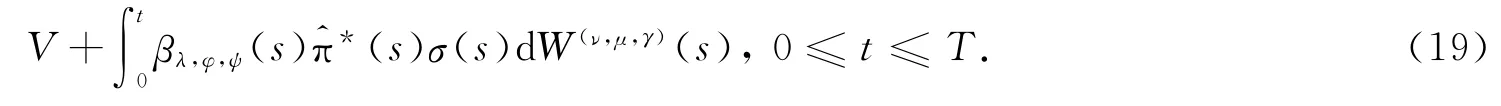
令（ν，μ，γ）≡0，则（19）式变为：

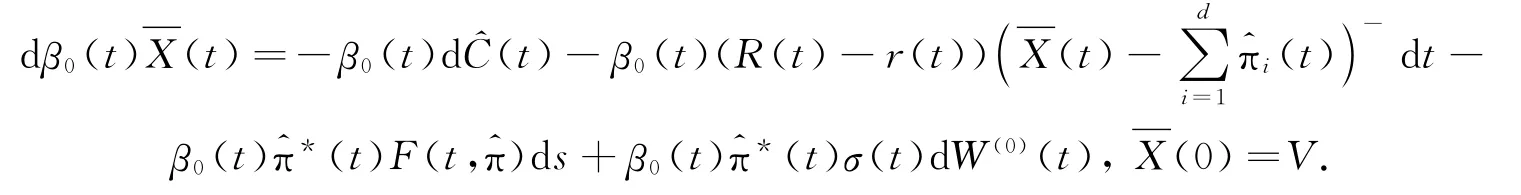
因此得XV，＾π，Ĉ（·）＝（·）.再由（19）式知∈A＋（V）.由（·）≥B（·）≥0知XV，＾π，Ĉ（τ）＝（τ）≥B（τ），∀τ∈φ，因此V∈U，hup（K）≤V＜∞.

定理证明完毕.

用类似方法可得到美式未定权益的下套期保值价格，进而可得到美式未定权益的无套利价格区间.

［1］Mckean H.A free boundary problem for the heat equation arising from a problem in mathematical economics［J］.Industr Manag Rev，1965（6）：32－39.

［2］Bensoussan A.On the theory of option pricing［J］.Acta Appl Math，1984（2）：139－158.

［3］Karatzas I.On the pricing of American options［J］.Appl Math Optimiz，1988（7）：37－60.

［4］Karatzas I，Kou S G.Hedging American contingent claims with constrained portfolios［J］.Finance stochast，1998（2）：215－258.

［5］Cvitanic J，Karatzas I.Convex duality in constrained portfolio optimization［J］.Anns Appl Probab，1992（2）：767－818.

［6］Cvitanic J，Karatzas I.Hedging contingent claims with constrained portfolios［J］.Anns Appl Probab，1993（3）：652－681.

［7］Karatzas I，Kou S G.On the pricing of contingent claims under constraints［J］.Anns Appl Probab，1996（6）：321－369.

［8］孟庆欣，劳兰珺，赵学雷.有摩擦金融市场中的美式未定权益定价［J］.应用概率统计，2008，24（5）：450－462.

［9］刘光中.凸分析与极值问题［M］.北京：高等教育出版社，1991.