主动转向干预时质心侧偏角的估计策略

魏建伟，赵万忠，尚伟燕

(1.宁波工程学院机械工程学院，浙江宁波315016;2.南京航空航天大学能源与动力学院，江苏南京210016)

从使用的传感器信号、成本和估计精度等方面对现有的质心侧偏角估计方法进行评价，可以得到如下结论:①某些传感器的成本比较高，而且需要特定的安装方式，不适于配置在量产车上;② 采用转向盘转角信号来反映转向系统的角位移特性［1］，适用于机械转向系统和助力转向系统.

主动转向主要包括变传动比控制和横摆角速度控制，其本质上都是施加独立于驾驶员的附加转角控制，即通过改变转向系统的角位移传递特性实现的［2-3］.因而对于具有主动转向功能的转向系统而言，由于主动转向干预改变了转向系统的角位移传递特性，则转向盘转角与质心侧偏角内在对应关系在主动转向干预工况下不再成立，使得传统的基于转向盘转角信号的质心侧偏角估计方法，不再适用于基于主动转向干预工况时汽车行驶状态参数的估计.

为解决上述估计策略的技术缺陷，笔者结合齿轮齿条转向器的机械结构特点，采用转向小齿轮转角来反映转向系统的角位移特性，并提出将质心侧偏角看作是转向小齿轮转角和车辆质心侧向加速度的非线性映射的估计策略.利用CarSim软件进行双移线和蛇形试验，并将获得的虚拟试验数据作为训练样本数据和验证样本数据，验证提出的估计策略的有效性，并与传统基于转向盘转角信号的质心侧偏角估计方法进行对比分析.

1 角位移传递特性分析

转向系统总角位移传动比可以定义为转向盘转角 θsw与前轮转角 δf的比值［4］，其数学表达式为

对于机械转向系统和助力转向系统而言，转向系统的传动比由转向系统转向器的机械结构决定，一般为固定值或在很小范围内变化.假定转向器的机械传动比为G，则取i=G.

主动转向通过施加独立于驾驶员的附加转角θac，改变转向小齿轮转角θp输出，进而改变了前轮转角δf的大小.此时，转向小齿轮转角θp和前轮转角 δf［5］分别为

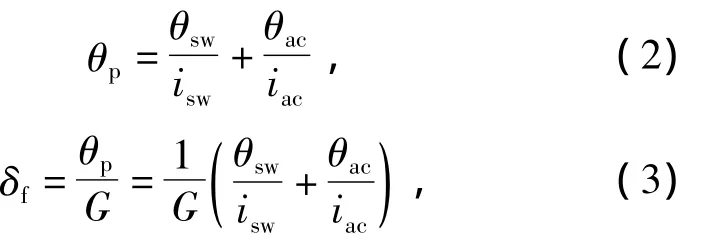
式中isw和iac分别为转向盘和主动转向执行电动机到转向小齿轮的减速比.

根据式(1)所阐述的转向系统总角位移传动比的定义，可以得到主动转向干预时转向系统总角位移传动比为

2 估计策略和估计算法

2.1 估计策略及可行性分析

传统的质心侧偏角估计策略将质心侧偏角看作是转向盘转角和车辆质心侧向加速度的非线性映射，不再适用于主动转向干预工况时汽车行驶状态参数的估计.结合齿轮齿条转向器的机械结构特点，以及现有宝马主动转向系统中采用的总转向角传感器［6-7］，可以用来测量转向小齿轮转角.因此，采用转向小齿轮转角来反映转向系统的角位移特性，并将质心侧偏角看作是转向小齿轮转角和车辆质心侧向加速度的非线性映射的研究方案是可行的.

2.2 估计算法的选择及基本理论

由于汽车的行驶工况复杂多变，所以要求质心侧偏角的估计算法具有良好的泛化能力，以弥补部分行驶工况训练样本难以获得的不足.现有研究成果表明:基于自适应模糊神经推理系统(adaptive neuro-fuzzy inference system，ANFIS)算法进行汽车状态参数估计具有较好的泛化能力.

因转向小齿轮转角能完整反映转向系统的角位移传递特性，将该算法用于质心侧偏角的估计，将汽车质心侧偏角看作是转向小齿轮转角和车辆质心侧向加速度的非线性映射.并采用2输入、单输出的1阶Sugeno模糊推理系统分别进行质心侧偏角的估计，其推理过程可以等效为如图1所示的ANFIS结构.

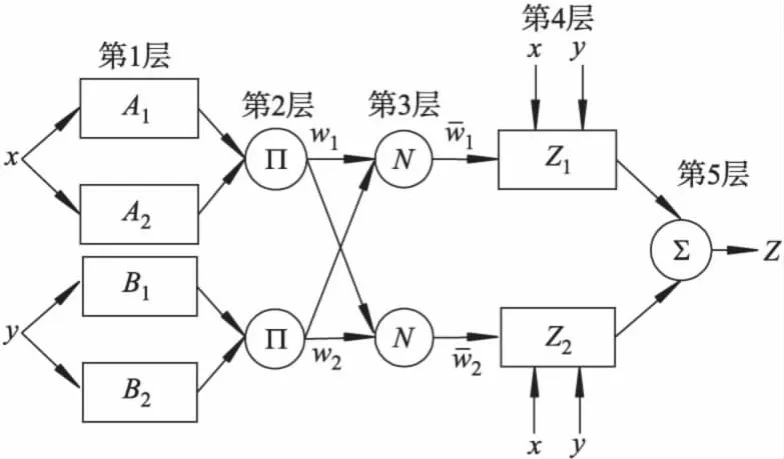
图1 模糊推理系统等效ANFIS结构

定义x为转向小齿轮转角，y为车辆质心侧向加速度，Z为质心侧偏角的估计值，对应的规则［8-9］为

规则1 如果转向小齿轮转角x为A1，车辆质心侧向加速度y为B1，则Z1=p1x+q1y+r1，其中p1，q1，r1为算法拟合参数.

规则2 如果转向小齿轮转角x为A2，车辆质心侧向加速度y为B2，则Z2=p2x+q2y+r2，其中p2，q2，r2为算法拟合参数.

各层功能如下:

第1层:该层每个节点将输入变量模糊化，输出对应模糊集的隶属度.输出函数为

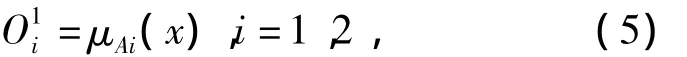
式中μAi(x)为广义钟形隶属度函数，取值范围为0≤μAi(x)≤1，并满足:

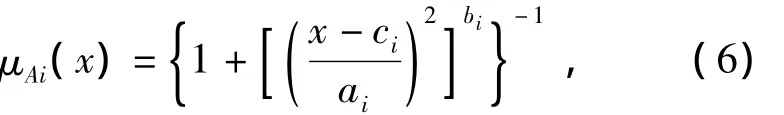
或

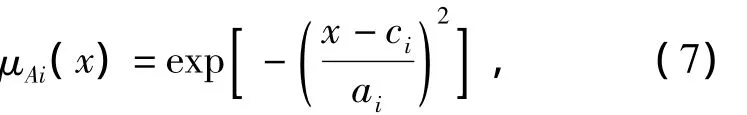
式中{ai，bi，ci}为参数组，或称之为前件参数.

第2层:该层节点以Π为标记，将输入信号相乘并输出计算结果，该层每个输出节点满足如下输出函数:

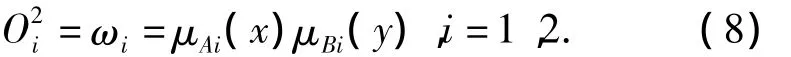
第3层:该层节点以N为标记，第i个节点计算第i条规则可信度的归一化值为

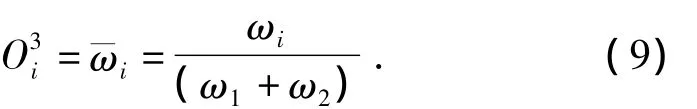
第4层:计算每条规则的输出为

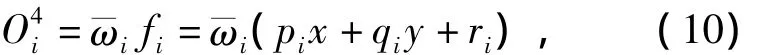
第5层:该层节点以∑为标记，计算所有输入的总输出，即质心侧偏角估计值.

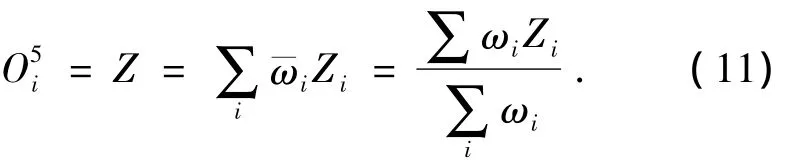
输出值与参考值的差值被用于调整结论参数.给定前件参数，总输出可以表示为结论参数的线性组合，则所有输入的总输出，即质心侧偏角估计值可表示为

ANFIS的混合学习算法可以分为前向传播和反向传播.在前向传播中，功能信号一直传递到第4层，结论参数采用最小二乘(least-squares，LS)算法进行估计辨识;而在反向传播中，误差率被反向传播，基于梯度下降法进行前件参数更新.为训练和调整模糊推理系统(fuzzy inference system，FIS)，采用反向传播算法和最小二乘算法相结合的混合学习算法，其学习过程主要包括:①固定前件参数，利用最小二乘算法进行结论参数的辨识;② 固定结论参数，将误差从输出端反向传播到输入端，利用标准反向传播算法进行前件参数的更新.

3 样本数据的获得

为保证训练样本数据的正确性和可靠性，利用CarSim软件进行样本数据的获得.在CarSim软件中选择“D-Class，Sedan”作为原型车，且采用驾驶员控制模式为“constant target speed”以实现恒车速虚拟试验.试验道路的设置参考ISO 3888-1—1999《乘用车急剧改变车道的操纵用试验车道第1部分:两车道变换》和GB/T 6323.1—1994《汽车操纵稳定性试验方法蛇形试验》，道路轨迹的计算公式详见文献［10］.虚拟试验数据的获得主要包含无主动转向干预时样本数据的获得，以及有主动转向干预时样本数据的获得.

3.1 无主动转向干预时样本数据获得

无主动转向干预时样本数据的获得方法:设定CarSim原型车的机械角位移传动比G为16，按照设定的道路试验工况进行虚拟试验.提取转向盘转角、左前轮转角、右前轮转角、车辆质心侧向加速度和质心侧偏角虚拟试验值.按如下关系表达式进行转向小齿轮转角θp的计算:

式中δlf和δrf分别为左前轮转角和右前轮转角.

3.2 有主动转向干预时样本数据获得

为获取主动转向干预时的样本数据，采用CarSim和Simulink的联合仿真计算的方法.基于CarSim和Simulink联合仿真计算的通信界面如图2所示.

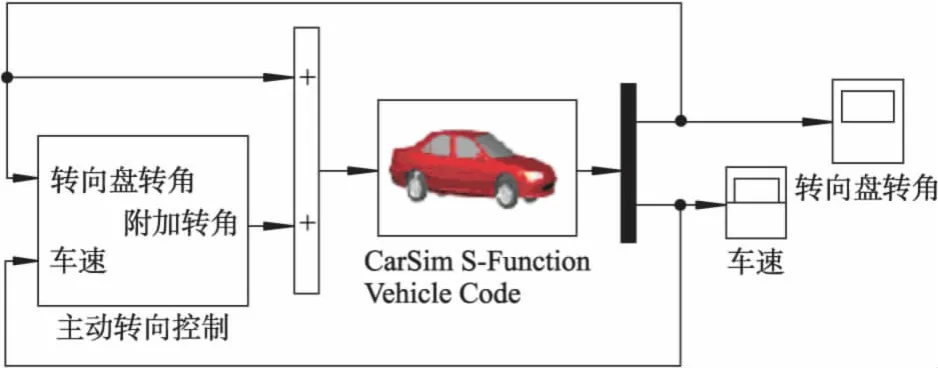
图2 CarSim与Simulink的联合仿真界面

将CarSim模型的输入设置为左、右前轮转角，与原系统信号的处理方式为“Add”，而输出设置为转向盘转角和车速.主动转向控制模块根据转向盘转角和车速，决策等效到左、右前轮的附加转角，以模拟主动转向干预工况.具体的决策逻辑可以由式(2)和(3)确定并表示为

式中转向系统总角位移传动比i取为20.

按照设定的道路试验工况进行虚拟试验，得到此时的转向盘转角、左前轮转角、右前轮转角、车辆质心侧向加速度和质心侧偏角虚拟试验值.转向小齿轮转角θp仍可以由式(13)确定.

4 估计策略的验证

为验证在有无主动转向干预时提出的估计策略的有效性，分别进行双移线和蛇行试验验证.

4.1 双移线试验验证

选取车速分别为70，90 km·h-1时双移线道路虚拟试验数据作为训练样本数据，对基于ANFIS算法的模糊推理系统进行训练.将车速为80 km·h-1时双移线道路虚拟试验数据用做验证样本数据，不同估计策略的质心侧偏角的估计值和理想值的对比曲线如图3所示，“1”表示理想值，“2”表示传统基于转向盘转角信号的估计策略，“3”表示文中提出的估计策略.

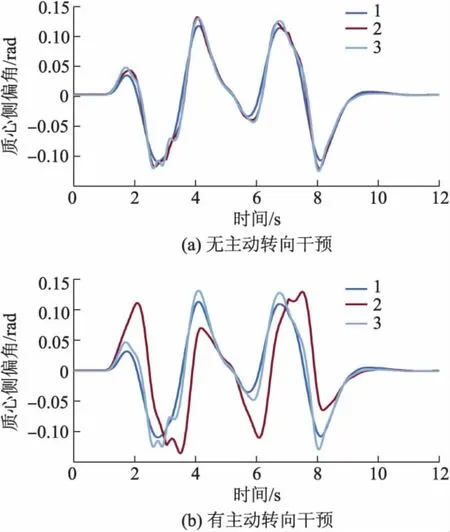
图3 双移线工况验证结果

由图3a可以看出:无主动转向干预时，传统基于转向盘转角信号的估计策略以及提出的估计策略均能有效地进行质心侧偏角的估计，估计误差绝对值的平均值分别为 5.8 ×10-3，6.6 ×10-3rad，估计误差绝对值的均方差分别为7.0×10-3，7.7×10-3rad.因此，在无主动转向干预时，2种估计策略具有相近的估计精度.

由图3b可以看出:有主动转向干预时，采用传统的基于转向盘转角信号的估计策略得到的质心侧偏角估计值与实际值存在较大的偏差，估计误差绝对值的平均值及均方差分别为 3.4 ×10-2，4.2 ×10-2rad，而采用文中提出的估计策略得到的质心侧偏角估计值与实际值的吻合程度较好，估计误差绝对值的平均值及均方差分别为 7.0 ×10-3，7.8 ×10-3rad，因此仍具有较好的估计精度.

4.2 蛇行试验验证

为进一步验证提出的估计策略的有效性，选取车速分别为50，70 km·h-1时的蛇行试验数据作为训练样本数据，对基于ANFIS算法的模糊推理系统进行训练.并将车速为60 km·h-1时的蛇行试验用做验证样本数据，不同估计策略的质心侧偏角估计值和理想值的对比曲线如图4所示.

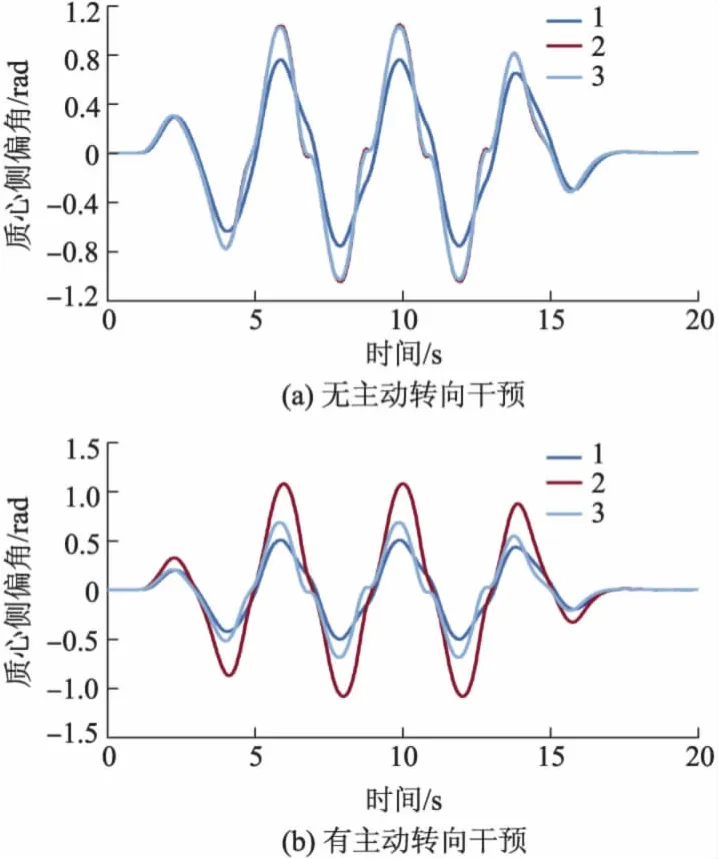
图4 蛇形线工况验证结果

由图4a可以得到与无主动转向干预时双移线工况验证结果相同的结论，即无主动转向干预时传统基于转向盘转角信号的估计策略与文中提出的估计策略均有效，估计误差绝对值的平均值分别为7.2 ×10-2，6.8 ×10-2rad，估计误差绝对值的均方差分别为6.3 ×10-2，6.0 ×10-2rad，因此具有相近的估计精度.

同样，由图4b可以得到与有主动转向干预时双移线工况验证结果相同的结论，即主动转向干预时，传统的基于转向盘转角信号的估计策略无法准确地进行质心侧偏角的估计，估计值与实际值存在较大的偏差，估计误差绝对值的平均值及均方差分别为1.9 ×10-1，2.0 ×10-1rad，而采用文中提出的策略所得到的质心侧偏角估计值，其估计误差绝对值平均值及均方差分别为 7.2 ×10-2，6.3 ×10-2rad，因此仍具有较好的估计精度.

由上述双移线和蛇行试验工况的估计结果可知:提出的估计策略在有、无主动转向干预的工况下均有效，且具有良好的估计精度和适用性.因而提出的质心侧偏角估计策略能有效地解决主动转向干预时的汽车状态参数估计问题.

5 结论

1)结合主动转向所装配的转向小齿轮转角传感器和齿轮齿条式转向器的结构特点，提出了将质心侧偏角看作是转向小齿轮转角和车辆质心侧向加速度的非线性映射的估计策略，解决了主动转向干预时质心侧偏角的估计问题.

2)利用CarSim软件进行了双移线和蛇行试验，得到的虚拟试验数据验证了文中提出的质心侧偏角估计策略的有效性.

3)提出的质心侧偏角的估计策略和研究成果，对汽车状态参数的估计具有一定的参考价值.

References)

［1］Kato M，Isoda K，Yuasa H.Estimation of vehicle side slip angle with artificial neural network［J］.JSAE Review，1994，15(1):79-82.

［2］魏建伟，魏民祥，赵万忠.融合主动转向功能的动力转向系统综述［J］.机械科学与技术，2011，30(6):913-917.Wei Jianwei，Wei Minxiang，Zhao Wanzhong.A review of power steering systems integrated with active steering［J］.Mechanical Science and Technology for AerospaceEngineering，2011，30(6):913-917.(in Chinese)

［3］冯 冲，丁能根，何勇灵.汽车ABS与AFS集成控制算法［J］.江苏大学学报:自然科学版，2013，34(2):138-143.Feng Chong，Ding Nenggen，He Yongling.Integrated control algorithm of ABS and AFS for automobile［J］.Journal of Jiangsu University:Natural Science Edition，2013，34(2):138-143.(in Chinese)

［4］Millsap S A，Law E H.Handling enhancement due to an automotive variable ratio electric power steering system using model reference robust tracking control［C］∥SAE Technical Paper Series.USA:SAE Publication Group，Paper Number:960931.

［5］Reinelt W，Klier W，Reimann G，et al.Active front steering(part 2)，safety and functionality［C］∥SAE Technical Paper Series.USA:SAE Publication Group，Paper Number:2004-01-1101.

［6］Klier W，Reinelt W.Active front steering(part 1):mathematical modeling and parameter estimation［C］∥SAE Technical Paper Series.USA:SAE Publication Group，Paper Number:2004-01-1102.

［7］葛小铭.宝马E60主动转向系统结构与检修［J］.汽车维修技师，2006(7):20-21.Ge Xiaoming.Maintenance and structure of active steering system for BMW E60［J］.Auto Maintenance，2006(7):20-21.(in Chinese)

［8］Mar J，Lin F J.An ANFIS controller for the car-following collision prevention system［J］.IEEE Transactions on Vehicular Technology，2001，50(4):1106-1113.

［9］Jang J S R.ANFIS:adaptive-network-based fuzzy inference system［J］.IEEE Transactions on Systems，Man and Cybernetics，1993，23(3):665-685.

［10］Zong Changfu，Guo Konghui，Guan Hsin.Research on closed-loop comprehensive evaluation method of vehicle handling and stability［C］∥SAE Technical Paper Series.USA:SAE Publication Group，Paper Number:2000-01-0694.