硬点对悬架和操稳性能灵敏度分析及鲁棒性优化

高 晋，杨秀建，牛子孺

(昆明理工大学交通工程学院，云南昆明650500)

灵敏度是指设计参数变更对设计性能指标影响的定量评估［1-4］.鲁棒性是指系统受到干扰时仍能保持其设计目标的性质.鲁棒性是属于质量工程的范畴，质量工程强调在设计时就考虑产品的质量问题，核心思想是质量不是靠检测和控制生产过程得到的，而是以产品的质量为直接目标导向通过设计得到的，为了获得鲁棒性质量要求，需要降低系统对输入参数的敏感度，因此灵敏度分析是鲁棒性设计的基础.笔者基于某研发车型，分析其悬架硬点坐标对悬架性能指标和稳态操稳指标的敏感度，并对悬架性能指标进行鲁棒性优化设计.

1 仿真分析过程

仿真分析基于Isight软件，与ADAMS，MATLAB软件联合来实现.通过Isight软件的DOE模块，来驱动ADAMS求解输出结果，再经过MATLAB计算得到需要的性能指标，包括悬架K特性指标、操稳指标.具体来讲，首先在ADAMS中建立悬架和整车的多体动力学仿真模型.然后通过 Isight软件的DOE模块研究硬点坐标对悬架和整车操稳性能指标的敏感程度，包括参数研究和正交试验.参数研究是分析一个设计参数对性能指标的影响，而正交试验则是通过特殊的试验方案来分析和比较多个硬点坐标对目标性能的影响大小.最后基于上述灵敏度分析结果对悬架性能指标进行鲁棒性优化设计.

2 悬架K特性灵敏度分析

悬架K特性，即悬架的运动学特性，是指车轮在上下运动过程中，悬架的性能参数随车轮跳动的关系.包括车轮前束角、外倾角、轴距和轮距等悬架性能指标随车轮跳动的关系.通常有平行轮跳工况和反向轮跳工况.进行灵敏度分析的悬架为一典型的双横臂悬架，由上下控制臂及转向拉杆组成，双横臂悬架模型如图1所示.

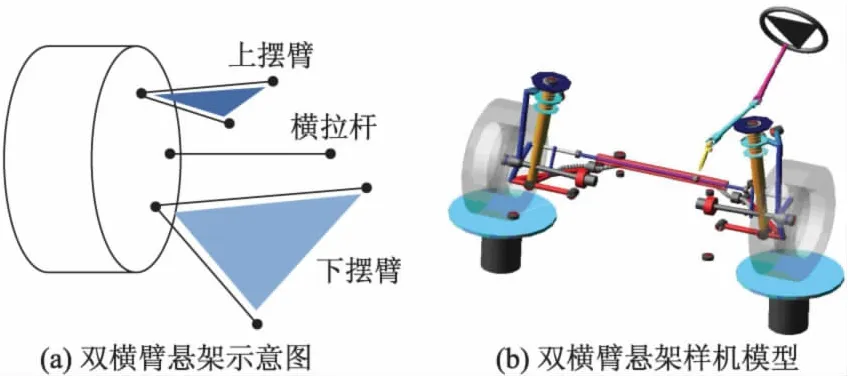
图1 双横臂悬架模型

对仿真模型进行平行轮跳分析，轮跳行程为［-80 mm，80 mm］.下面将分析硬点坐标对悬架性能指标影响的大小［5］，包括车轮前束角、外倾角、轴距、轮距、侧倾中心高度和抗点头率.

对于车轮前束角、外倾角、轴距和轮距，通常分析轮跳行程为［-25 mm，25 mm］时，性能指标参数的变化率，即变化梯度.侧倾中心高度、抗点头率则考察在设计载荷时的值.前束角、外倾角随轮跳的变化曲线分别如图2，3所示，图中标出了在［-25 mm，25 mm］的轮跳范围内，2个指标的变化梯度.对于前悬架，一般来说，前束变化应为负向斜率，即前束变化梯度为负值.轮跳外倾对轮胎附着情况和轮胎偏磨有较大影响，为了提高附着力，外轮要内倾，内轮要外倾，因此轮跳外倾应为负向斜率.同时，变化梯度不应过大，以免轮胎偏磨.

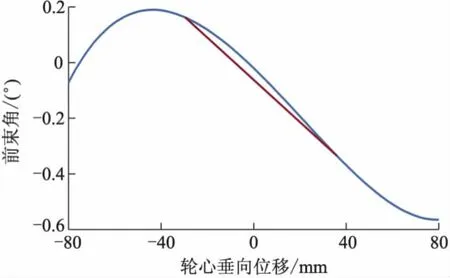
图2 前束角随轮跳变化曲线

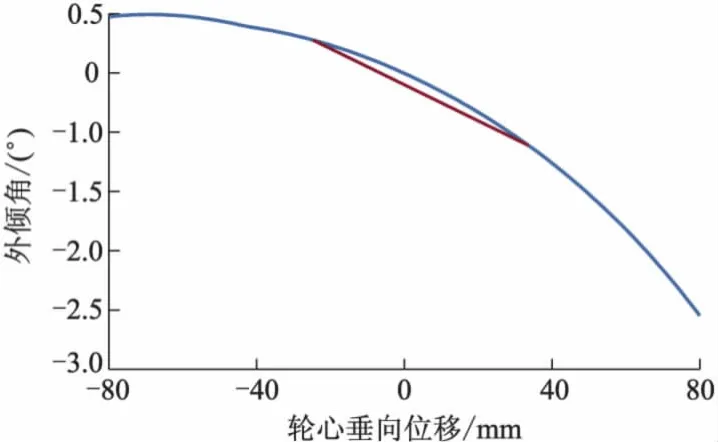
图3 外倾角随轮跳变化曲线

通过分析，得出前束角和外倾角梯度与硬点坐标关系曲线分别如图4，5所示.从图4可以看出:转向横拉杆内外连接球头点z向坐标对前束角变化梯度最为敏感，降低转向横拉杆内球头高度，前束角变化梯度会增大，而降低转向横拉杆外球头高度，前束角变化梯度会减小，因此前束角变化梯度和内外连接球头点的高度差有关.从图5可以看出:上控制臂前点和外点z向坐标对外倾角变化梯度最为敏感，上控制臂前点z向坐标减小，外倾角变化梯度会增大.上控制臂外点z坐标减小，外倾角变化梯度会减小.对外倾角变化梯度影响较大的其他几个坐标方向分别是上控制臂后点z向，下控制臂前点z向、下控制臂外点z向以及转向横拉杆内点z向.可见，无论前束角还是外倾角，都是硬点z方向坐标对其变化较为敏感.

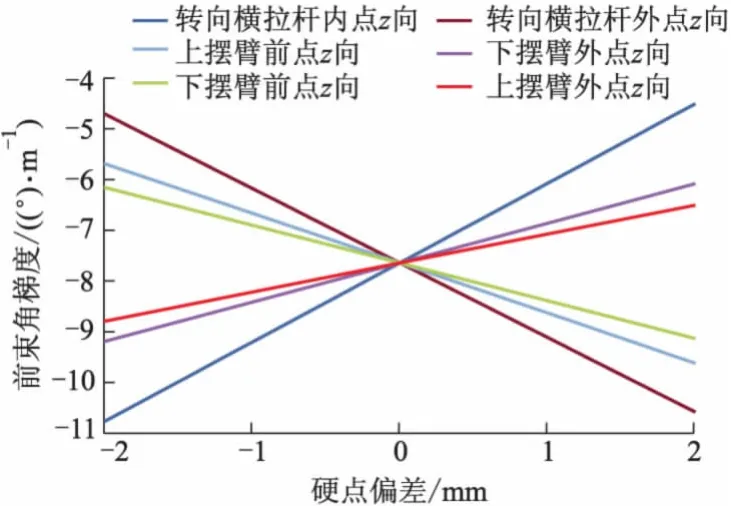
图4 前束角梯度与硬点坐标关系

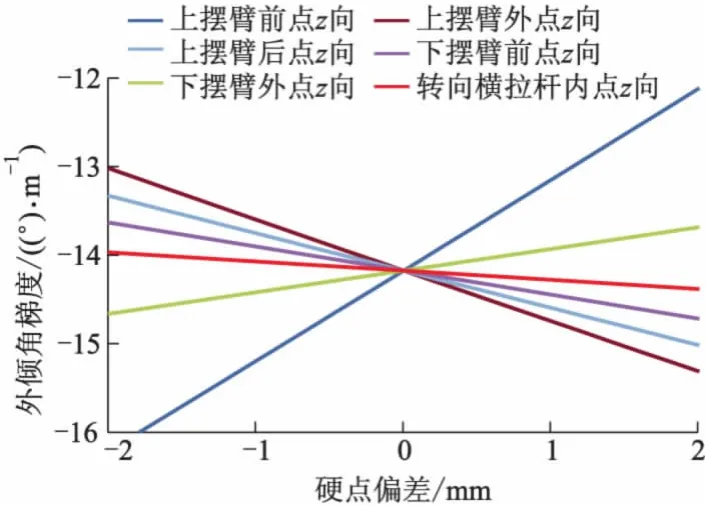
图5 外倾角梯度与硬点坐标关系

硬点坐标对前束角和外倾角梯度的灵敏度大小比较分别如图6，7所示，A1为转向横拉杆内点z向，A2为转向横拉杆外点z向，A3为上摆臂前点z向，A4为下摆臂外点z向，A5为下摆臂前点z向，A6为上摆臂外点z向，A7为上摆臂后点z向.

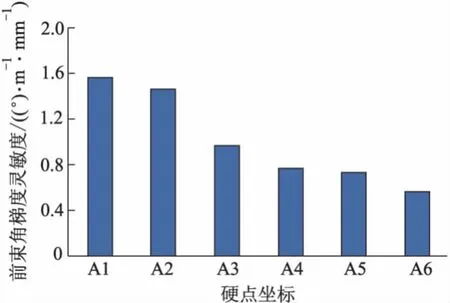
图6 硬点坐标对前束角梯度的灵敏度大小比较

图7 硬点坐标对外倾角梯度的灵敏度大小比较

从提高平顺性的角度，对于前悬架来说，当经过凸块时，前轮心应向后退让，轴距减小.因此，轮跳轴距变化应为正向斜率.同时为防止轮胎的环磨，轴距变化梯度不宜过大.轮距变化会影响轮胎的磨损，在正常工作范围内，轮距变化要尽量小.轴距、轮距变化梯度与硬点坐标偏差的关系分别如图8，9所示.从图8可以看出下控制臂前点和下控制臂后点z向坐标对轴距变化最为敏感.

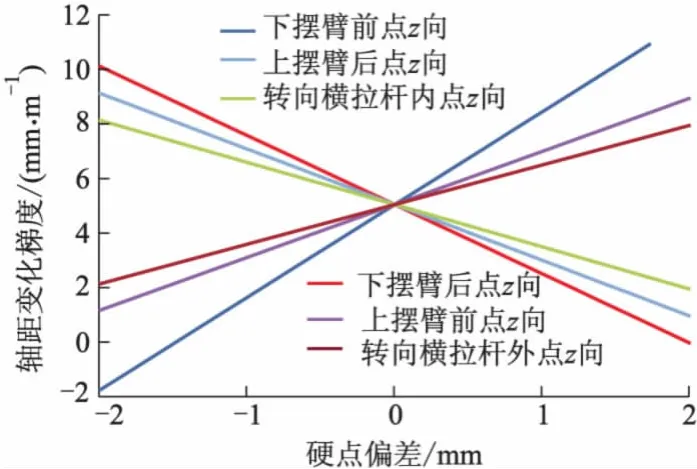
图8 轴距变化梯度与硬点关系

图9 轮距变化梯度与硬点关系

侧倾角反映车身侧倾的程度，侧倾中心高度影响车辆转弯时的侧倾角大小.侧倾中心高度低，车辆重心绕侧倾轴线的力臂大，会使车辆的侧倾角增大，不利于车辆的稳定性.侧倾中心高度与硬点坐标偏差的关系如图10所示，可见，下控制臂前点对侧倾中心高度最敏感.

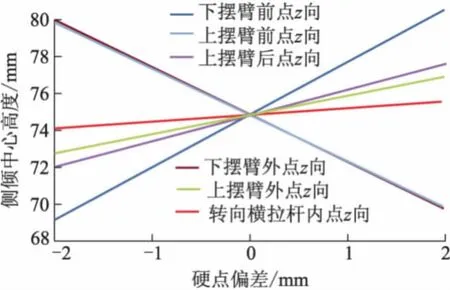
图10 侧倾中心高度与硬点关系

通过仿真分析得到转向横拉杆内外点z向坐标对悬架性能指标的敏感度数值如表1所示.

表1 悬架性能指标灵敏度

3 转向特性灵敏度分析

对转向特性指标，分析了悬架硬点坐标对车轮20°转角时的阿可曼百分比、车轮锁止时的阿可曼百分比以及最小转弯半径的灵敏度.对模型进行转向分析时，齿条的行程为［-76 mm，76 mm］.仿真得到的最小转弯直径与车轮转角的关系如图11所示.

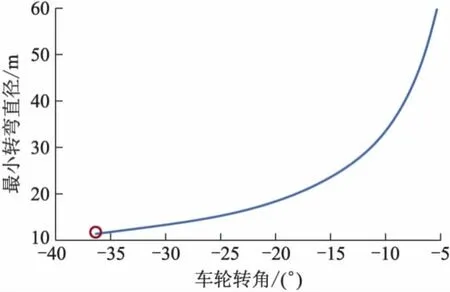
图11 最小转弯直径与车轮转角关系

车轮转角20°时和车轮锁止时阿可曼转角与硬点坐标偏差的关系分别如图12，13所示.可见，转向横拉杆外点y向对阿可曼百分比最敏感.

图12 车轮转角20°时阿可曼百分比与硬点坐标关系

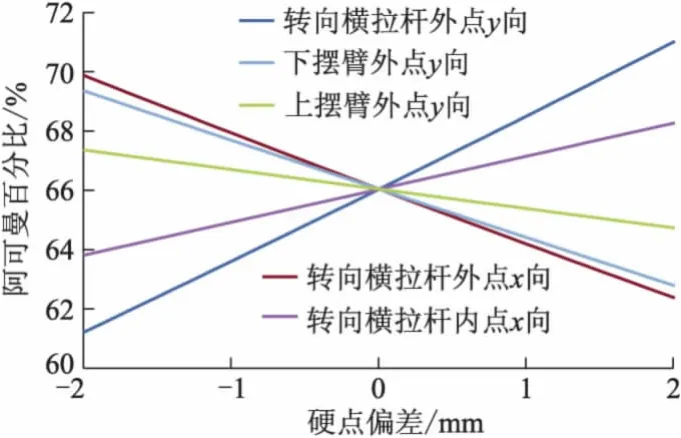
图13 车轮锁止时阿可曼百分比与硬点坐标关系

最小转弯直径与硬点坐标偏差的关系如图14所示.硬点坐标对最小转弯直径灵敏度比较如图15所示，B1为转向横拉杆外点x向，B2为下控制臂外点x向，B3为转向横拉杆外点y向，B4为下摆臂外点y向，B5为上摆臂外点x向.可以看出转向横拉杆外点x向对最小转弯直径最敏感.

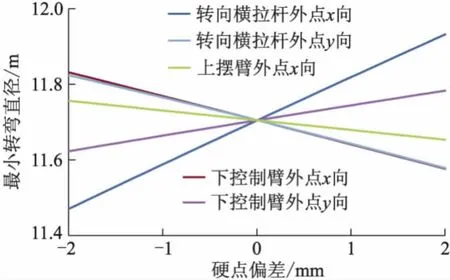
图14 最小转弯直径与硬点坐标关系

图15 硬点坐标对最小转弯直径的灵敏度比较

4 整车操稳灵敏度分析

在ADAMS中建立整车仿真模型，整车模型的前悬架为双横臂模型，后悬架为一空间多连杆悬架.整车的建模参数如表2所示.

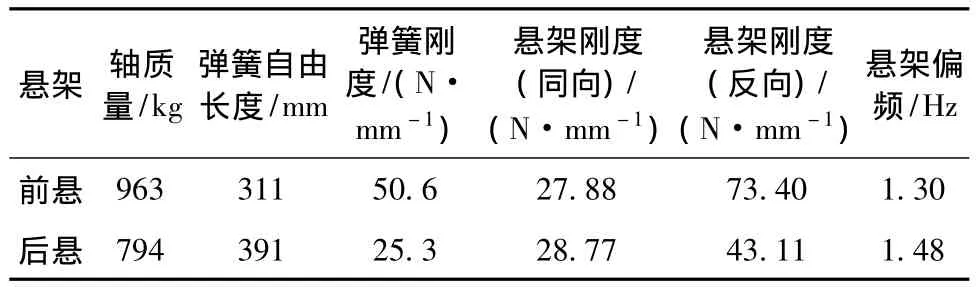
表2 整车参数

进行的整车稳态操稳仿真为定半径稳态回转.方向盘转角、车身侧倾角与侧向加速度的仿真和试验对比曲线分别如图16，17所示，g为重力加速度.从试验和仿真的对比结果可以看出:在进行稳态操纵稳定性分析时，仿真模型具有很高的精度，因此用仿真模型来研究硬点坐标对整车操稳指标的敏感度有很好的可信度.

图16 方向盘转角与侧向加速度关系

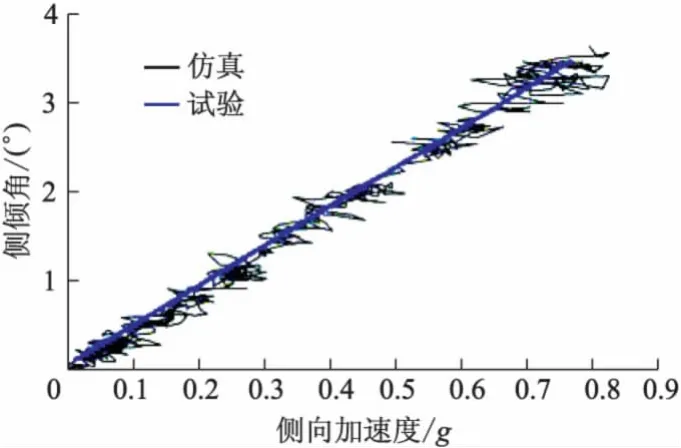
图17 侧倾角与侧向加速度关系

稳态操稳分析的指标包括最大侧向加速度ay、不足转向度和侧倾角梯度［6］.其中，不足转向度为侧向加速度ay对方向盘转角θsw曲线在0.4g时的斜率，侧倾角梯度为侧倾角φ对侧向加速度曲线在0.4g时的斜率.

稳态不足转向度为

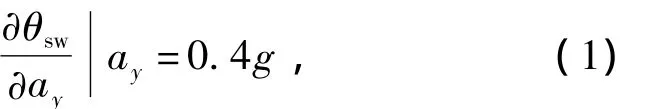
稳态侧倾角梯度为

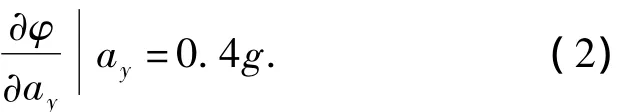
仿真得到的最大侧向加速度与转向横拉杆内点z向坐标偏差关系如图18所示，转向横拉杆内点降低，最大侧向加速度增大.

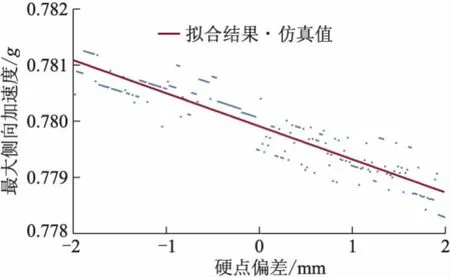
图18 最大侧向加速度与转向横拉杆内点坐标偏差关系

不足转向度与转向横拉杆内点z向坐标偏差的关系如图19所示，转向横拉杆内点降低，不足转向度增大.不足转向度大，说明同样的方向盘转角，车辆的侧向加速度小，即车辆的稳定性更好.从上面悬架的灵敏度分析可知:转向横拉杆内点降低，轮跳转向梯度增大.据此，从理论上分析可知整车的不足转向特性会增大.因此，悬架和整车的灵敏度分析结果是一致的.

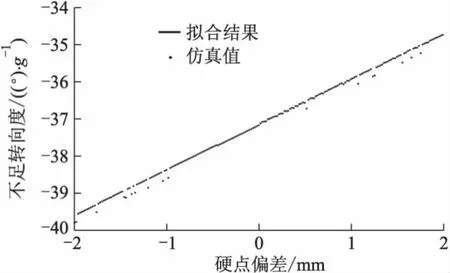
图19 不足转向度与转向横拉杆内点z向坐标偏差关系

通过分析，转向横拉杆内外点z向坐标对稳态操稳性能指标的敏感度数值如表3所示.

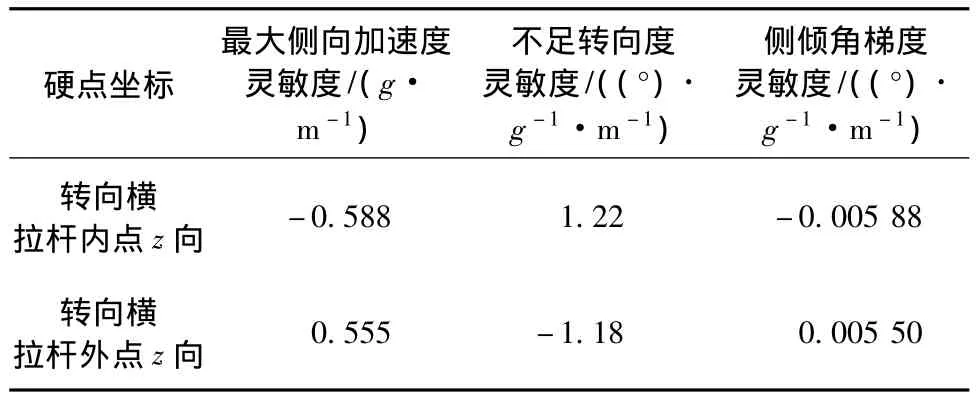
表3 稳态操稳指标灵敏度

5 正交试验设计

正交试验［7-8］的特点是各因素中的每个水平在所有试验中出现的次数相同，正交表的任何2列所有可能出现的数对均出现，并且出现的次数相同，下面将通过正交试验分析硬点对悬架性能指标的影响.并对比上文通过参数研究法得到的灵敏度分析结果.

正交试验分析的性能目标有前束角、外倾角、轴距、轮距、抗点头率和侧倾中心高度.其中抗点头率、轮距、侧倾中心高度为设计载荷时的值，其他参数为车轮在整个跳动过程中的变动量.悬架性能指标如表4所示.正交试验对试验的因素和水平有要求，因此，首先通过主效应分析来选择对性能指标影响较大的硬点坐标方向，然后再进行正交试验分析.主效应分析时每个硬点的坐标设计为2个水平.

表4 悬架性能指标

对悬架硬点进行主效应分析，筛选对悬架性能影响较大的硬点坐标.根据主效应分析求得的对各悬架性能指标影响最大的硬点坐标方向如表5所示.

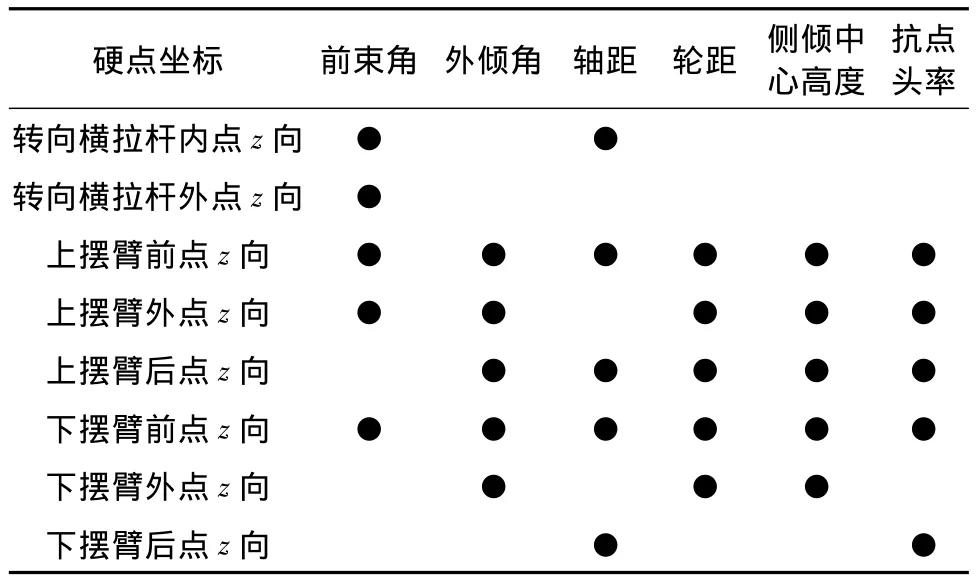
表5 悬架性能主效应分析结果

根据表5的分析结果，分别选择对各个悬架性能指标影响最大的5个硬点坐标方向.其中每个硬点坐标方向选择4个水平，分别是［-2 mm，-1 mm，1 mm，2 mm］，因此这是一个L16(45)试验.

根据正交试验得到的前束角、外倾角、轴距、轮距、抗点头率和侧倾中心高度性能指标如表6所示.

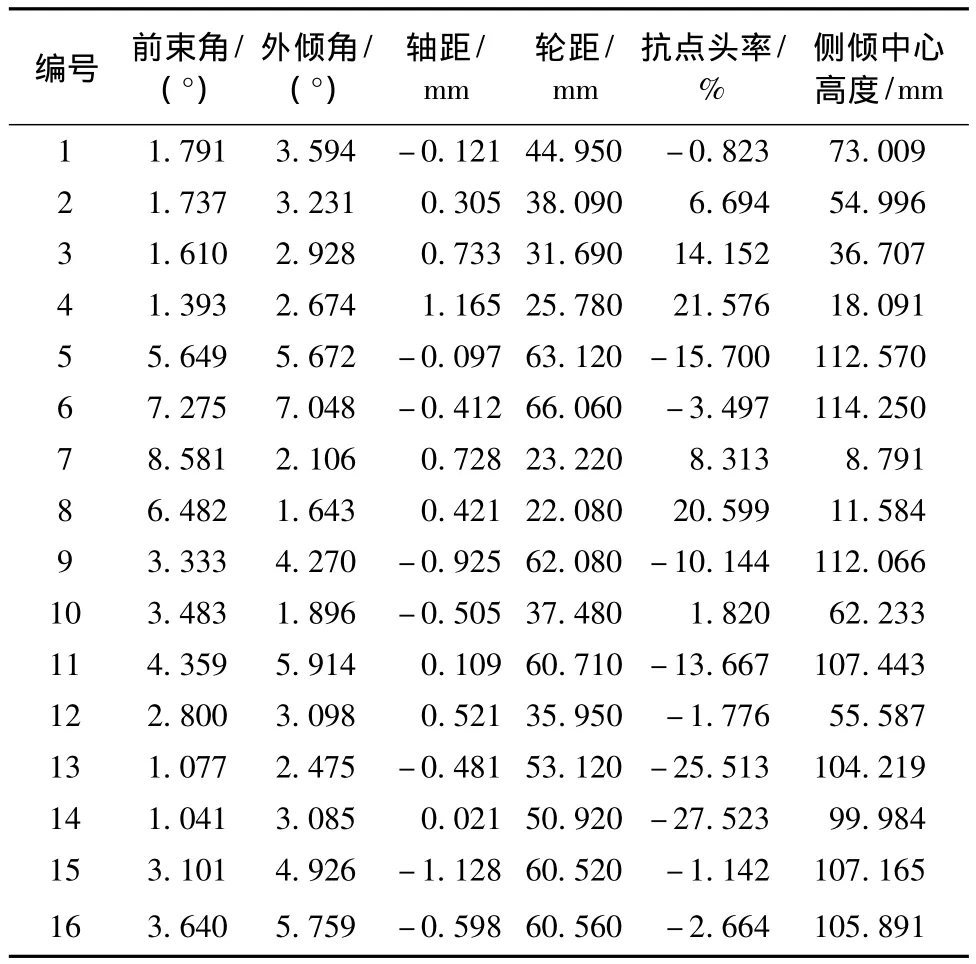
表6 正交试验分析结果

根据正交试验结果得到的前束角、外倾角的综合平均值和极差如表7，8所示.文中仅给出了前束角、外倾角的综合平均值和极差.其中:Ki=∑Koi为试验中某一水平对应的目标性能之和为综合平均值;极差R=max{Ki}-min{Ki}，反映不同的因素(设计参数)对目标性能的影响大小，极差大则对目标性能影响就大.

根据表7的正交试验分析结果可知:对前束角影响最大的依次是转向横拉杆内点z向，转向横拉杆外点z向，上摆臂前点z向，下摆臂外点z向，下摆臂前点z向.这与上文参数研究法的分析结论一致.同样对于外倾角等其他悬架性能参数可以得到相同的结论.

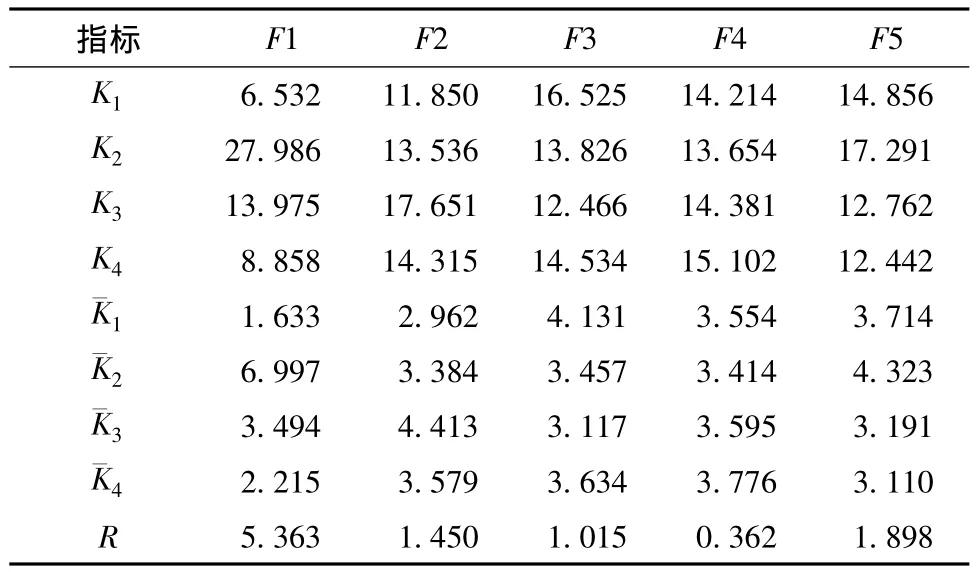
表7 前束角综合平均值和极差

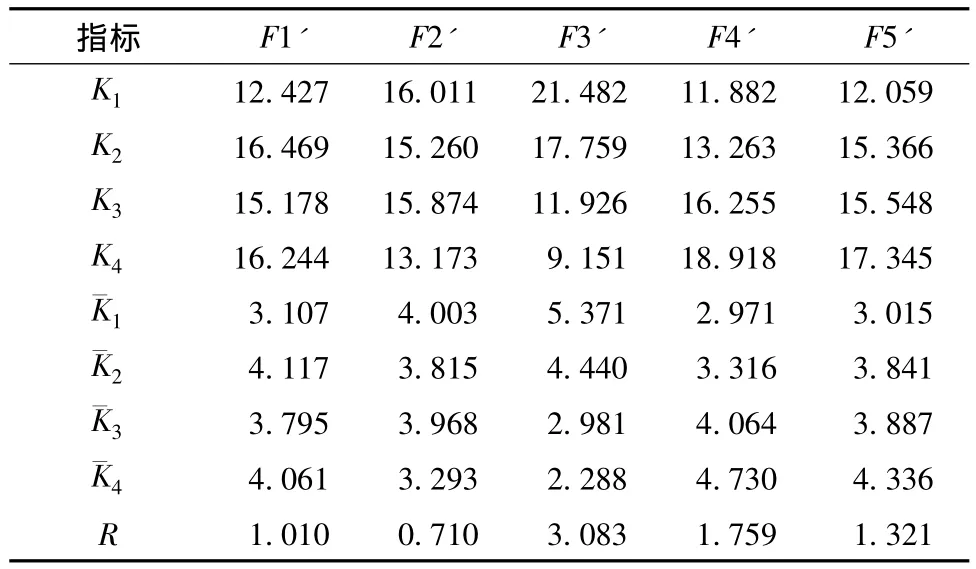
表8 外倾角综合平均值和极差

6 鲁棒性优化

优化分为确定性优化和鲁棒性优化.确定性优化是在设计空间中寻找最优解，而最优解并不一定是最稳定的解，往往在最优解集中，设计参数很小的变动，会使性能目标发生很大的变异，这是设计所不希望的.鲁棒性优化则是寻找更稳定的解［9-10］.

借助Isight软件的6σ模块，对悬架性能指标进行稳健性优化，悬架性能指标和上文分析的指标相同.6σ是质量工程中提出的概念，强调在产品设计阶段，减小由于误差噪声引起的质量偏差和变异，减小误差对性能参数的敏感性，并以σ水平评价质量的稳健性和可靠性，优化策略如下:

优化目标为

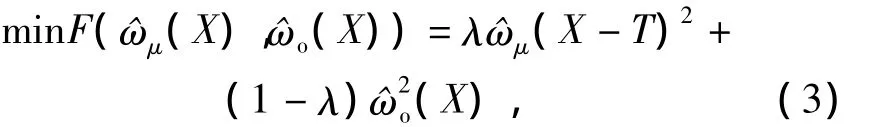
约束条件为

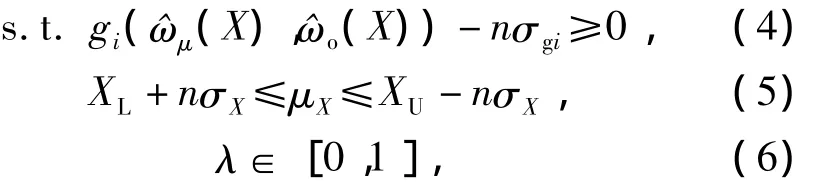
式中:均值T为性能目标均值的期望目标值;^ωμ(X)为性能目标函数;^ωo(X)为性能目标方差;λ为权因子，通过合理选择权因子，平衡优化响应的均值和方差;σgi为不同约束的方差;XL，XU为设计变量的容差上下限;σX为设计变量的方差.

优化通过引入性能目标的标准差，以不同的σ水平、可靠度、失效概率作为评价可靠性优化的指标.可靠度是指性能目标在约束条件内的概率，失效概率是指性能目标超出设计约束条件的概率.

根据灵敏度分析结果，选择对悬架所有性能指标综合影响最大的5个硬点坐标方向，假设其制造和安装误差为正态分布，据此求出悬架性能指标的分布，然后确定性能指标的约束条件，对硬点坐标进行优化，得到优化后的悬架性能指标分布.

优化前后的部分悬架性能指标分布对比分别如图20-25所示，优化后悬架性能指标分布在容差上下限外的概率下降，悬架性能更稳健.

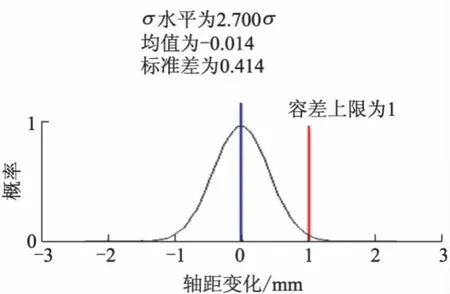
图20 优化前轴距变化分布

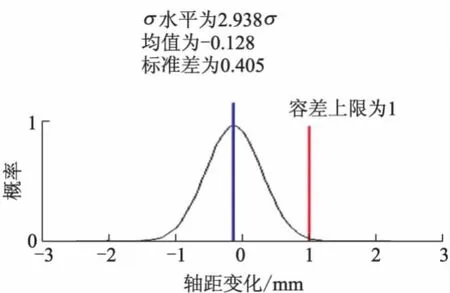
图21 优化后轴距变化分布

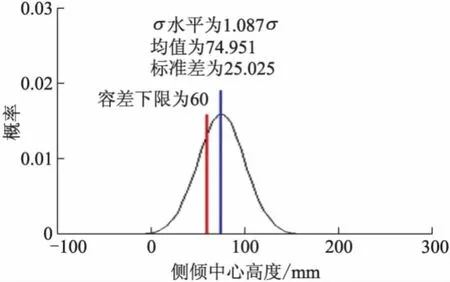
图22 优化前侧倾中心高度分布

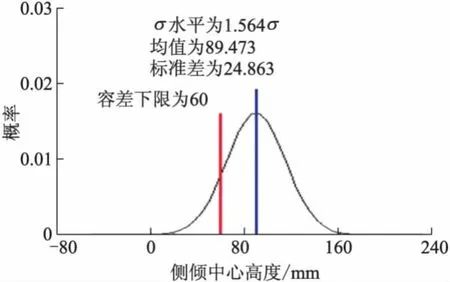
图23 优化后侧倾中心高度分布

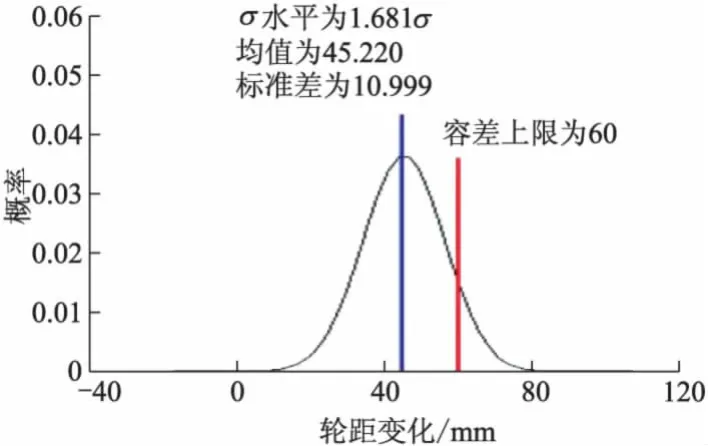
图24 优化前轮距变化分布

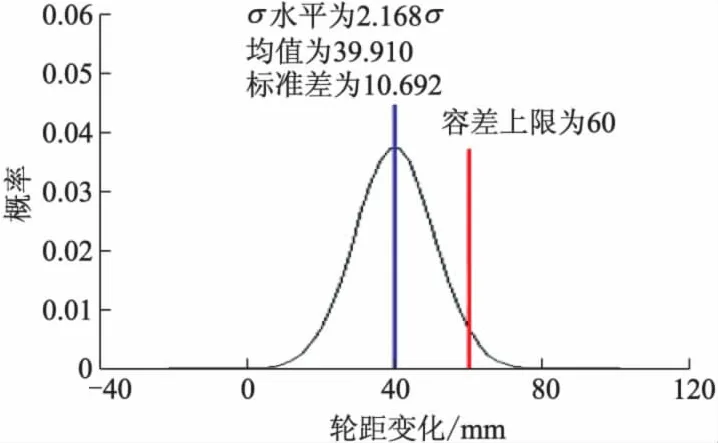
图25 优化后轮距变化分布

优化前后的悬架性能指标的可靠性分析结果如表9，10所示.可见，优化后悬架性能指标的水平提高、在容差范围内的可靠度增大、失效概率降低.

表9 优化前可靠性分析结果

续表

表10 优化后可靠性分析结果

7 结论

1)利用灵敏度分析方法可以精确定量地评估硬点坐标对轮跳时悬架运动指标和转向性能参数影响的大小，并且能够在硬点坐标偏差范围内直观地显现性能指标随硬点坐标偏差变化的趋势.将灵敏度分析方法运用到操纵稳定性的研究上，可以分析操纵稳定性指标诸如侧倾角梯度、最大侧向加速度等与硬点安装坐标偏差的直接关系，能直观地揭示悬架特性对整车操稳性能影响的机理.

2)通过合理设计正交试验研究硬点坐标对悬架性能的影响，能够简单快速地找到对性能指标影响较大的硬点坐标方向，并将大大缩减参数研究法难以完成的计算量.这作为判定影响悬架性能关键硬点坐标的分析方法有很高的可靠度.

3)从稳健设计的角度，通过约束硬点坐标的偏差范围，基于硬点坐标的正态分布规律，利用6σ稳健优化方法重塑硬点位置，可以使悬架的各项性能指标变异更小，悬架的可靠度提高、由硬点偏差引起的性能不稳定的概率下降.

References)

［1］刘伟忠.基于虚拟样机技术的某车悬架K＆C特性仿分析及硬点优化［D］.吉林大学汽车工程学院，2009.

［2］张云清，陈 宏，项 俊，等.麦克弗逊前悬架参数灵敏度分析及优化［J］.机械设计与制造，2005(4):25-27.Zhang Yunqing，Chen Hong，Xiang Jun，et al.Sensitivity analysis and optimization of macpherson suspension［J］.Machinery Design＆Manufacture，2005(4):25-27.(in Chinese)

［3］陈 宏.基于实验设计的麦克弗逊悬架参数灵敏度分析及调校［D］.华中科技大学机械科学与工程学院，2005.

［4］方志刚，过学迅，左 磊，等.馈能型悬架潜力研究及其敏感性分析［J］.江苏大学学报:自然科学版，2013，34(4):373-377.Fang Zhigang，Guo Xuexun，Zuo Lei，et al.Potential study and sensitivity analysis of energy-regenerative suspension［J］.Journal of Jiangsu University:Natural Science Edition，2013，34(4):373-377.(in Chinese)

［5］刘慧斌.Strut-Links型后悬架硬点及衬套刚度优化方法的研究［D］.吉林大学汽车工程学院，2011.

［6］宗长富，郭孔辉.汽车操纵稳定性的客观定量评价指标［J］.吉林大学学报:自然科学版，2000，30(1):1-6.Zong Changfu，Guo Konghui.Objective evaluation index for handling and stability of vehicle［J］.Journal of Jilin University:Natural Science Edition，2000，30(1):1-6.(in Chinese)

［7］董俊红，成艾国.基于试验设计的某微型客车悬架参数匹配优化［J］.科学导报，2010，28(14):75-79.Dong Junhong，Cheng Aiguo.Optimization and matching of mini passenger car suspension parameters based on design of experiment［J］.Science and Technology Review，2010，28(14):75-79.(in Chinese)

［8］Sushma Y，Sridhar M，Avinash D.Experiments planning for the robust design through CAE［C］∥SAE Technical Paper Series. USA:SAE Publication Group， Paper Number:2006-01-3518.

［9］Tu Jian，Cheng Yipen.An integrated stochastic design framework using cross-validated using cross-validated multivariate metamodeling methods［C］∥SAE Technical Paper Series.USA:SAE Publication Group， Paper Number:2003-01-0738.

［10］李玉强，崔振山，陈 军，等.基于双响应面模型的6σ稳健设计［J］.机械强度，2006，28(5):690-694.Li Yuqiang，Cui Zhenshan，Chen Jun，et al.Six sigma robust design mefhodology based on dual response surface model［J］.Journal of Mechanical Strength，2006，28(5):690-694.(in Chinese)