基于GCI的离心泵网格的收敛性

刘厚林，刘明明，白 羽，杜 辉，董 亮

(江苏大学流体机械工程技术研究中心，江苏镇江212013)

随着计算机技术及计算流体动力学(computational fluid dynamics，CFD)的发展，数值模拟已成为改进和优化离心泵设计的一个重要手段［1-3］.随着CFD研究与应用的深入，所面对的问题越来越复杂，对计算可信度的要求越来越高，确保计算可信度的难度也越来越大，计算可信度研究在国际上受到了空前的重视.在CFD研究与应用过程中，如何评估数值误差并转换为对用户有用的信息，使用户信任所获得的结果，这是CFD发展到今天所必须面对的问题［4］.数值误差包括建模误差、离散误差和计算误差，其中建模误差是从物理现象抽象到数学模型过程中引入的，离散误差取决于离散方程的截断误差以及网格的疏密程度，计算误差则包括迭代不完全误差和舍入误差.一般迭代不完全误差与舍入误差在数值误差中所占的比例很小，数值误差主要是由截断误差及网格划分不够细密所造成的，而当离散格式的截断误差确定以后，网格的疏密及其分布特性就成了决定离散误差的关键因素.

目前，数值误差评估的方法有很多［5-8］.但使用最多的是由 P.J.Roache［9］提出通过计算网格收敛指数(grid convergence index，GCI)来评估数值误差的方法.计算GCI至少需要3套疏密不同的网格，一般网格越密，离散解越接近精确解，从而离散误差越小，GCI值也越小.目前，很多研究者通过GCI对数值计算误差进行了相关研究，特别是在流体传热、流体机械、圆管流动等方面取得了一些成果.M.Karimia等［10］利用GCI对旋液分离器进行误差分析，并分析了GCI中的关键参数对数值误差的影响.郑秋亚等［11］针对M6机翼的绕流问题，对5套不同网格的CFD模型进行计算，并使用Richardson外推法评估数值误差，就网格密度对人工耗散和解的影响进行了分析.康顺等［12］以高压比离心压气机中的离心叶轮为例进行了3套不同网格的数值模拟，通过对不同密度网格模拟结果和试验值比较，从而分析和讨论网格密度对模拟结果的影响.刘重阳等［13］通过对光滑直圆管中黏性稳态等温流动进行不同尺寸网格的CFD计算，通过求解动量方程和湍流动能及湍流耗散率方程，比较流动充分发展段的数值解与精确解，给出了误差随网格尺寸的变化规律.

目前，对离心泵数值计算误差评估的相关研究较少，笔者在对一台离心泵分别划分结构网格、非结构网格及混合网格并进行数值计算的基础上，结合Richardson外推法进行网格收敛性研究，并对比分析不同网格类型下的离心泵内部流动，以期为以后提高离心泵CFD计算精度提供一定的依据.

1 网格收敛指数计算步骤

P.J.Roache［9］提出使用GCI来计算离散误差，该方法要求计算结果满足单调收敛条件，即0＜(f3-f2)/(f2-f1)＜1，式中:f为数值求解的离散解;下标1，2，3为由疏到密的3套网格.计算GCI的详细步骤如下.

对于k(k=1，2，3)网格的计算结果满足:

式中:fexact为数值求解的精确解;h为网格尺度;p为收敛精度;gp是不随网格变化的p阶误差项系数.定义网格细化比为

严格意义上，网格细化比应该选为2，但这对于成功的细化网格，往往是不切实际的，且非结构网格也很难控制网格尺寸.一般来讲，r的取值小于2.r值也可以用网格控制单元数的比率来计算:

式中N为网格的控制单元数.

定义2套网格之间的相对误差为

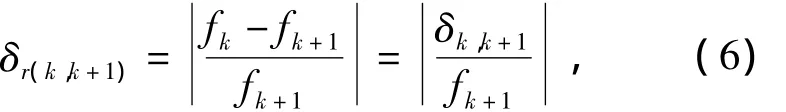
式中 δk，k+1=fk-fk+1.

如果忽略方程(1)-(3)中的高阶项，则p可以用下式求得:

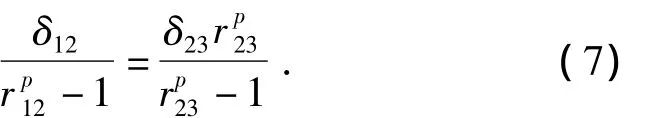
定义GCI为

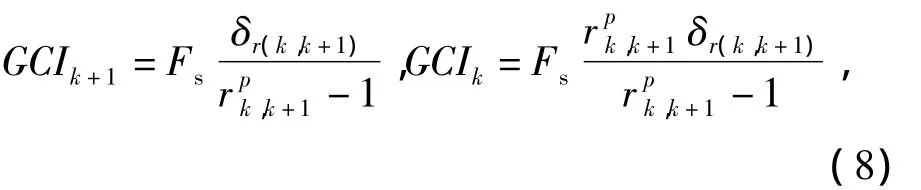
式中Fs为安全因子，一般取值范围为1.25～3.00，文中取 3.00.

2 数值方法

2.1 计算模型

研究对象为一台离心泵.泵的设计参数:流量Q=25 m3·h-1;扬程H=10 m;转速n=1 450 r·min-1;比转数ns=78.4.模型泵的主要尺寸参数:叶轮进口直径D1=75 mm;叶轮出口直径D2=200 mm;叶轮进口宽度b1=18 mm;叶片出口宽度b2=8 mm;蜗壳基圆直径D3=220 mm;叶片数Z=6;叶片包角D1=110°;进口安放角 β1=17.6°;出口安放角β2=40°，蜗壳出口宽度b3=11 mm.

2.2 网格划分

采用ICEM软件对模型泵分别划分3组不同网格尺度的结构六面体网格、非结构四面体网格及混合三棱柱/四面体网格，生成网格在泵中截面处的剖 面视图如图1所示.

图1 生成网格

2.3 数值计算

Ansys CFX软件因其收敛速度快而被选择进行定常全流场数值模拟，采用RNGk-ε湍流模型进行方程封闭.将叶轮水体所在区域设置为旋转流体区域，泵的额定转速为给定的旋转速度值，与叶轮接触的部件表面设置为自由滑移壁面，其他壁面均定义为无滑移固壁边界，壁面粗糙度设置为50 μm，进出口边界条件设置采用速度进口、自由出流出口.

3 计算结果及分析

3.1 网格收敛性

为评估计算误差，对数值解进行网格收敛性分析.以扬程作为变量，通过方程(1)-(8)计算p和GCI，计算结果如表1所示.

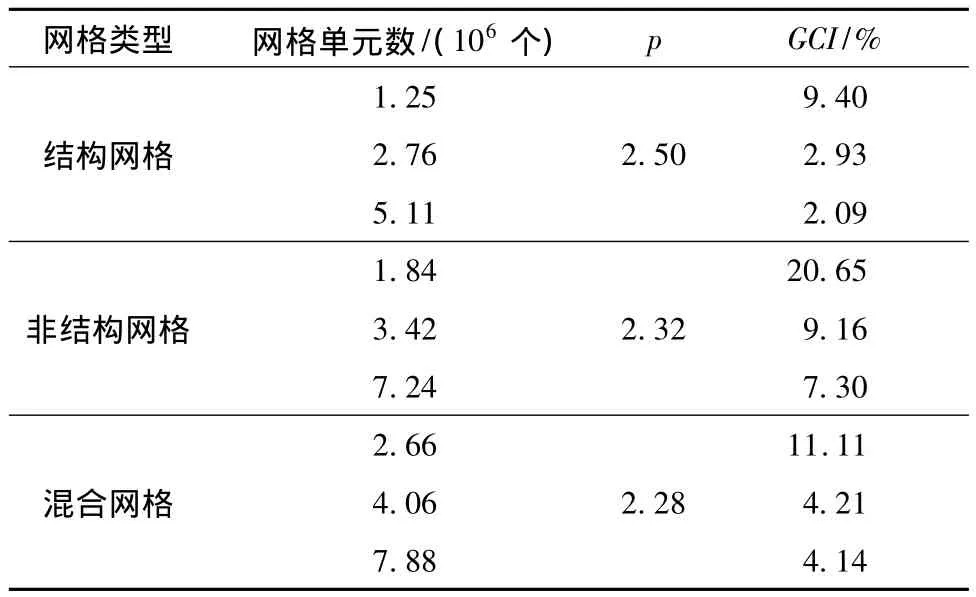
表1 结构网格下的计算结果

从表1可以看出:3种网格类型下p的计算结果相近，这是因为方程的收敛精度相同，这间接地说明了计算的准确性.3种类型的网格GCI随着网格的加密都不同程度地在减小，由于网格越密离散结果越接近精确解，因此离散误差越小，这表明3种类型的网格的加密是成功的.但不同网格类型之间的GCI计算值存在一定的差异.在网格单元数相近的情况下，结构网格计算的GCI值要大于混合网格，而混合网格的计算值要大于非结构网格，这表明:结构网格的计算精度较高，混合网格次之，非结构化网格与混合网格必须继续加密网格才能达到结构网格同等的精度.

3.2 叶轮内流场

为精确比较3种网格对离心泵内流场的影响，选择精度较高的计算扬程相对误差小于5%的单元数分别为5.11 ×106个的结构网格、7.24 ×106个的非结构网格以及7.88×106个的混合网格为研究对象.叶轮流道内的相对速度分布情况如图2所示，3种网格的相对速度分布有着很大程度的相似性，其中靠近隔舌的叶轮流道与其他流道有着很大的不同，其吸力面附近有着很大的低速区，而流道出口处则是一个高速区.相比较而言，3种网格的相对速度分布又有微小的差别，其中结构网格的叶轮流道内捕捉到了漩涡，而非结构网格与混合网格没有捕捉到漩涡.

图2 相对速度分布

3.3 蜗壳内流场

蜗壳内部速度分布情况及在截面1，2，3处的流线分布情况如图3-5所示.从速度云图上可以看出:3种网格的速度分布呈现一定的相似性，但相比结构网格与非结构网格，混合网格在蜗壳出口附近存在较大的低速区，且在截面2处出现与主流速度相反的速度.从截面1，2，3流线图可以看出:在截面1和截面2上，3种网格的流线分布相近，但在截面3上3种网格的流线分布存在明显的不同，比较而言，混合网格能够捕捉到更多的二次涡现象.

图3 结构网格蜗壳速度分布

图4 非结构网格蜗壳速度分布

图5 混合网格蜗壳速度分布

4 结论

1)随着网格的加密，GCI减小，且在网格单元数相近的情况下，结构网格计算的GCI要远小于非结构网格与混合网格的计算值.

2)在叶轮中截面的流道内，3种网格的流线分布相近，但相比非结构网格与混合网格，结构网格能够在靠近隔舌的叶轮流道里捕捉到漩涡.

3)在蜗壳中截面内，3种网格的速度分布情况相似，但混合网格在蜗壳出口处存在较大的低速区，且在蜗壳扩散段的某些截面处，混合网格能够捕捉到更多的二次涡现象.

References)

［1］杨敏官，孙鑫恺，高 波，等.离心泵内部非定常空化流动特征的数值分析［J］.江苏大学学报:自然科学版，2012，33(4):408-413.Yang Minguan，Sun Xinkai，Gao Bo，et al.Numerical analysis of unsteady cavitating flow characteristic in centrifugal pump［J］.Journal of Jiangsu University:Natural Science Edition，2012，33(4):408-413.(in Chinese)

［2］董 亮，刘厚林，谈明高，等.离心泵全流场与非全流场数值计算［J］.排灌机械工程学报，2012，30(3):274-278.Dong Liang，Liu Houlin，Tan Minggao，et al.Numerical calculation of whole and non-whole flow field in centrifugal pumps［J］.Journal of Drainage and Irrigation Machinery Engineering，2012，30(3):274-278.(in Chinese)

［3］Spence R，Amaral-Teixeira J.A CFD parametric study of geometrical variations on the pressure pulsations and performance characteristics of a centrifugal pump［J］.Computers＆Fluids，2009，38:1243-1257.

［4］杨 永.基于网格计算的 CFD模拟可信度分析［C］∥第十二届全国计算流体力学会议论文.北京:中国学术期刊电子出版社，2004:796-801.

［5］Oden J T，Babuška I，Nobile F，et al.Theory and methodology for estimation and control of errors due to modeling，approximation，and uncertainty［J］.Computer Methods in Applied Mechanics and Engineering，2005，194(2):195-204.

［6］Rabin Y.A general model for the propagation of uncertainty in measurements into heat transfer simulations and its application to cryosurgery［J］.Cryobiology，2003，46(2):109-120.

［7］Roy C J，Oberkampf W L.A comprehensive framework for verification，validation，and uncertainty quantification in scientific computing［J］.Computer Methods in Applied Mechanics and Engineering，2011，200(25):2131-2144.

［8］Oberkampf W L，Trucano T G.Verification and validation in computational fluid dynamics［J］.Progress in Aerospace Sciences，2002，38(3):209-272.

［9］Roache P J.Quantification of uncertainty in computational fluid dynamics［J］.Annual Review of Fluid Mechanics，1997，29:123-160.

［10］Karimia M，Akdogana G，Dellimoreb K H，et al.Quantification of numerical uncertainty in computational fluid dynamics modelling of hydrocyclones［J］.Computers and Chemical Engineering，2012，43:45-54.

［11］郑秋亚，王宝圆.网格密度对流场解的影响［J］.航空计算技术，2000，30(4):13-16.Zheng Qiuya，Wang Baoyuan.The influence of grid density to flow field soluation［J］.Aeronautical Computing Technique，2000，30(4):13-16.(in Chinese)

［12］康 顺，刘 强，祁明旭.一个高压比离心叶轮的CFD结果确认［J］.工程热物理学报，2005，26(3):400-404.Kang Shun，Liu Qiang，Qi Mingxu.CFD validation of high speed centrifugal compressor impeller［J］.Journal of Engineering Thermophysics，2005，26(3):400-404.(in Chinese)

［13］刘重阳，于 芳，徐让书.CFD计算网格误差分析的一个算例［J］.沈阳航空工业学院学报，2006，23(4):21-24.Liu Chongyang，Yu Fang，Xu Rangshu.A grid error analysis example in CFD［J］.Journal of Shenyang Institute of Aeronautical Engineering，2006，23(4):21-24.(in Chinese)