时滞细胞神经网络全局同步的滑模控制方法

蔡国梁，姚 琴，2，姜胜芹

(1.江苏大学非线性科学研究中心，江苏镇江212013;2.江苏物联网研究发展中心，江苏无锡224000)

1988 年，Leon O.Chua和 Yang Lin［1］提出了细胞神经网络，如今细胞神经网络已渐渐发展成为自然科学的一门新的学科分支.1992年，在Chua和Roska描述了具有时间延迟的细胞神经网络之后，时滞细胞神经网络取得了巨大发展，并逐渐成为神经网络领域里非常重要的分支.近年来，时滞细胞神经网络广泛应用于模式识别和信号传输.尤其是随着生物科学的迅猛发展，如今时滞细胞神经网络还扩展到信号分析、联想记忆和细胞模拟等方面.众所周知，时间延迟会导致系统不稳定、分叉或者振动.因此，时滞细胞神经网络的动力学分析就显得尤为重要.许多关于细胞神经网络具有时滞独立与时滞相关的稳定性［2-6］都被得到了证明，这些证明主要是基于Razumikhin技术、Lyapunov泛函和线性矩阵不等式等方法，而运用滑模控制方法的文献不多见.

近年来，滑模变结构控制方法［7］因其所具有的优良特性而受到越来越多的重视.该方法通过自行设计所需的滑模面和等效控制律，能快速响应输入的变换，而对参数变换和扰动不敏感，具有很好的鲁棒性，且物理制作简单.滑模变结构控制方法逐渐引起了学者们的重视，其最大优点是滑动模态对加在系统上的干扰和系统的摄动具有完全的自适应性，而且系统状态一旦进入滑模运动，便快速地收敛到控制目标，为时滞系统、不确定性系统的鲁棒性设计提供了一种有效途径，尤其是对非线性系统具有良好的控制效果.在文献［8］中，作者研究了具有时间延迟的异结构混沌神经网络的同步问题，考虑了系统具有复杂参数的情况，并且用滑模控制方法证明了相关结论.文献［9］成功利用滑模控制方法，考虑了具有多重时滞分布不对称Hopfield神经网络的全局同步问题.文献［10］应用滑模控制方法研究了具有混合时滞混沌神经网络的同步问题.仿真实例最终也充分证明了滑模控制方法的有效性.

文中将用改进的滑模控制方法来研究具有多时滞和分布时滞细胞神经网络的全局同步问题，时滞独立和时滞相关的情况都将被考虑到.

1 模型描述与原理

文献［11］考虑了具有多时滞和分布时滞的细胞神经网络的动态特性，利用 Lyapunov函数和Young不等式技术，研究了如下网络的全局渐近稳定性，其模型为

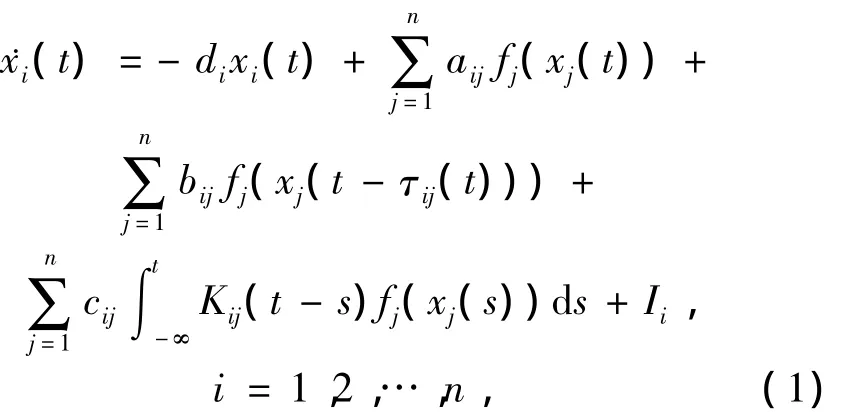
或者简写为

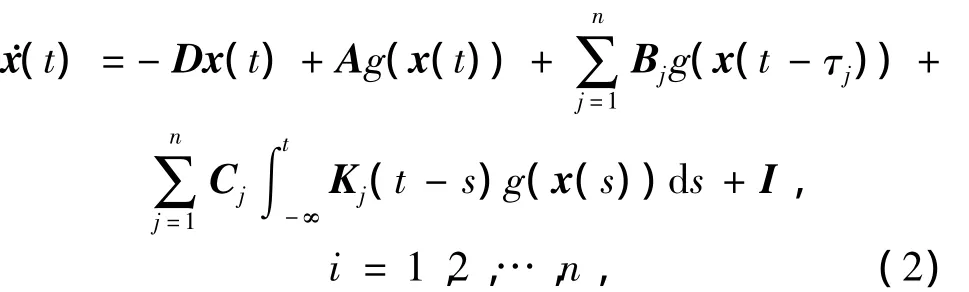
式中:xi(t)=［xi1(t)，xi2(t)，…，xin(t)］T∈Rn是第i个细胞神经节点在时间t的状态向量;D=(di)n×n表示各细胞神经节点的自反馈;A=(aij)n×n是无时滞状态细胞神经节点的连接系数矩阵;Bj=(bij)n×1是具有多时滞状态细胞神经节点的相关连接系数矩阵;激活函数f(xi)=0.5(|xi+1|+|xi-1|)是分段线性函数，且有界;τij(t)是多时滞，并且满足1-˙τj≤1;Cj=(cij)n×1是分布时滞细胞神经节点的连接权系数;I=［I1，I2，…，In］T是外部常值输入;核系数Kij:［0，∞)→［0，∞)在［0，∞)上分段连续并且满足:

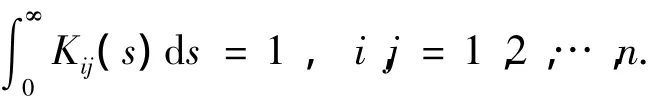
假定系统(1)的实际输出同时取决于具有多时滞和分布时滞的状态向量，满足如下形式:

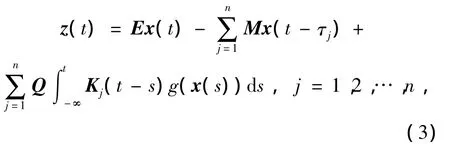
式中:z(t)∈Rm;E，M，Q∈Rm×n为已知常数矩阵.

假定系统(1)为驱动系统，则响应系统可以描述为

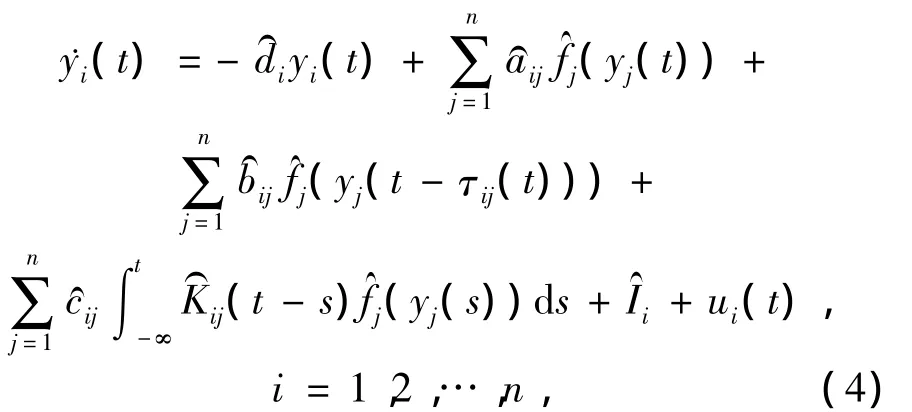
或者简写为

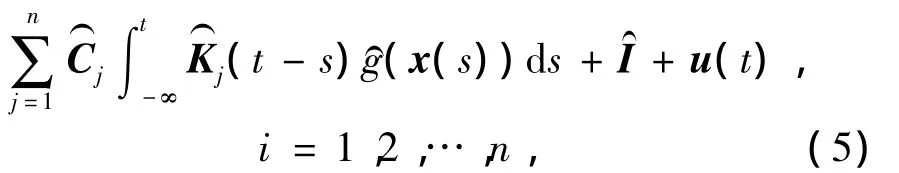
式中:y(t)∈Rn是响应系统的状态向量;u(t)是待定的滑模控制器.

定义误差为e(t)=x(t)-y(t)，下面的工作就是要设计一个合理的控制器，使得:当t→∞时，‖e(t)‖=‖x(t)-y(t)‖→0.系统(2)与系统(5)的误差系统为

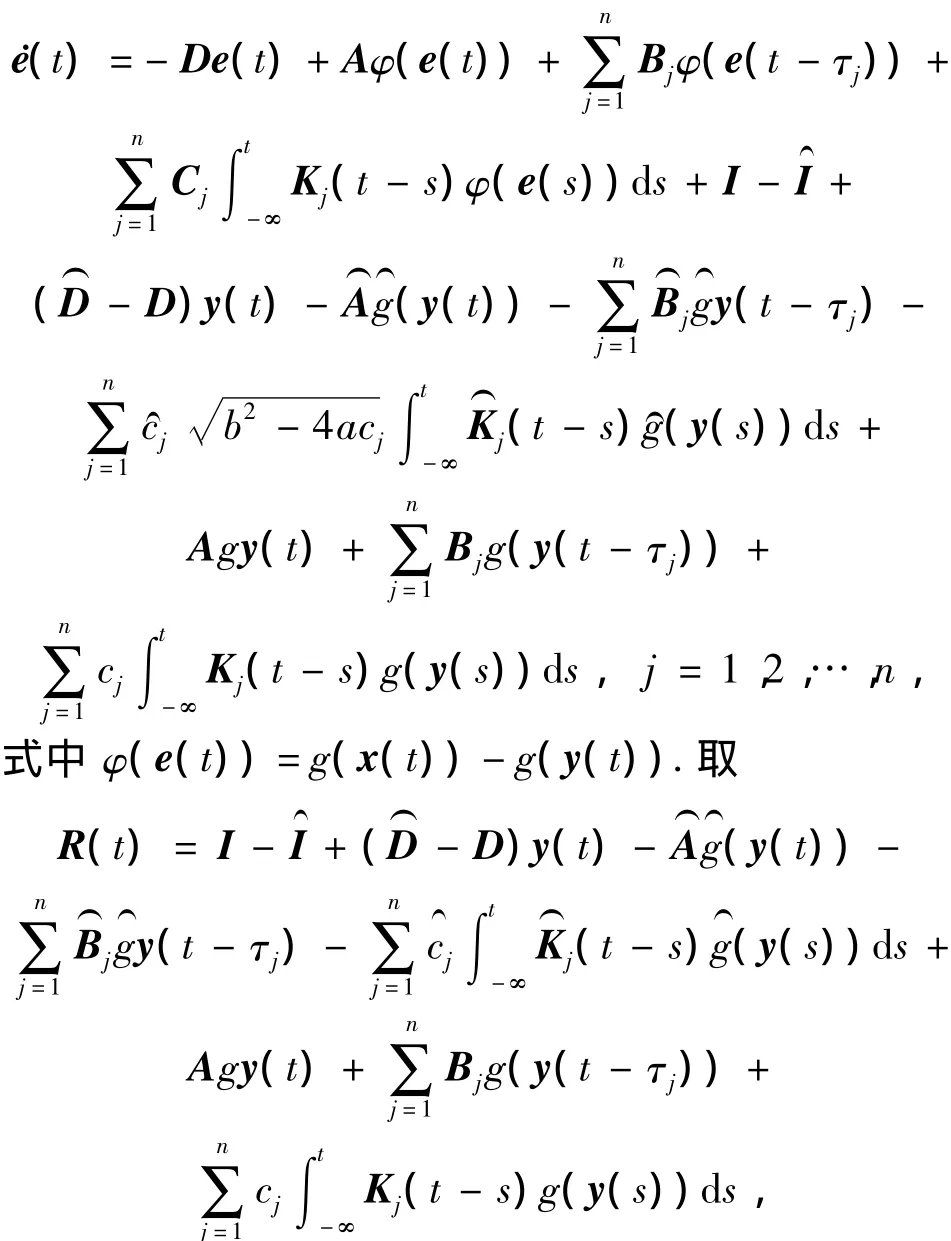
可以得到

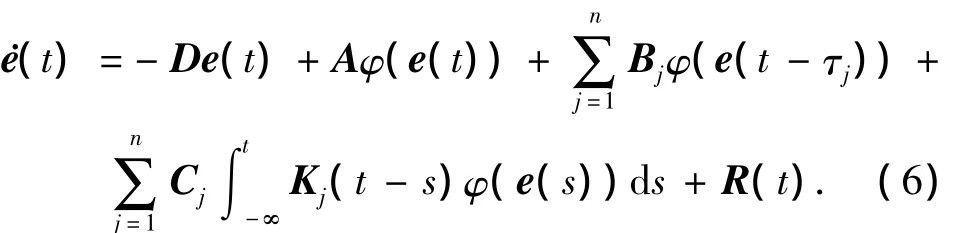
为文中证明需要，引用如下引理，该引理有别于文献［8］-［10］中关于激活函数的假设.

引理1［12］∀x(t)=［x1(t)，x2(t)，…，xn(t)］T，

y(t)=［y1(t)，y2(t)，…，yn(t)］T∈ Rn，存在正定矩阵P∈Rn×n，使得如下不等式成立:

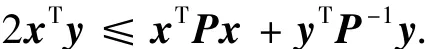
利用引理不难得到下面的命题:

命题1 ∀x(t)=［x1(t)，x2(t)，…，xn(t)］T，y(t)=［y1(t)，y2(t)，…，yn(t)］T∈Rn，∀Q为常数矩阵，满足如下不等式:

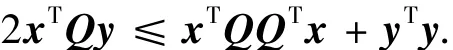
证明 由引理1，有:

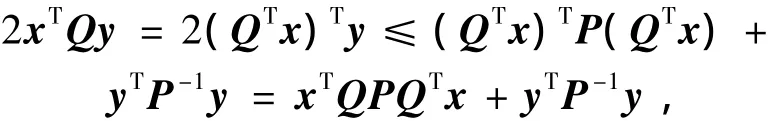
取P=I，可得

证毕.

2 滑模控制设计

滑模控制设计的基本思想是:对于系统(2)，选取适当的滑模控制器使得:(i)滑动模态是全局稳定的;(ii)系统(2)的状态轨迹全局达到滑模面并且持续保持在该滑模面上.

为了充分发挥实际输出值z(t)的作用，设计如下的滑模面:

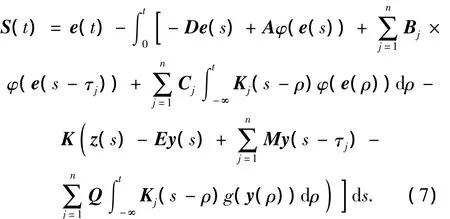
其中矩阵K∈Rm×n待定.由方程(6)可以得到:

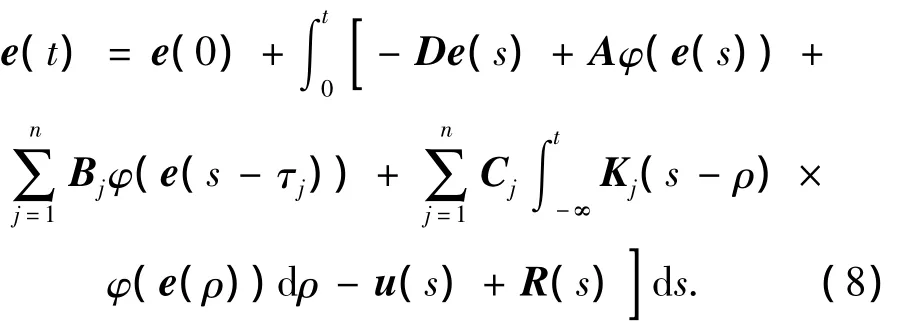
把式(8)代入式(7)，可以得到:

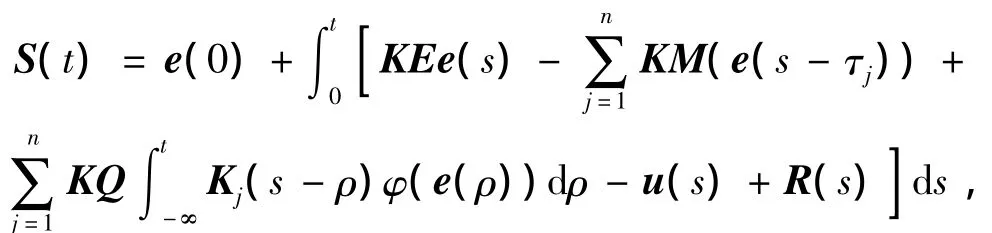
式中e(0)是误差系统(6)的初始值.

由滑模控制理论可知，当误差系统达到滑模面后，滑模控制器是一个极强的非线性输入，不利于分析.为使得分析更简单，用一个连续的等价输入来代替切换输入.当误差系统(6)的状态轨迹进入滑动面时，S(t)=0并且(t)=0.于是，得到如下等价的滑模控制器:

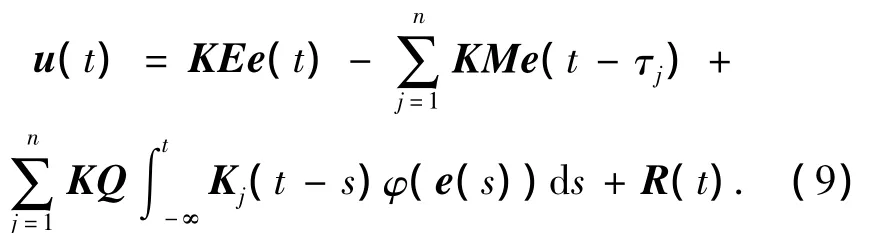
把式(9)代入式(6)，可以得到如下滑动模态:

研究系统(10)的稳定性，分别考虑系统(10)在时滞独立与时滞相关的情况下，全局稳定的条件.有如下定理:

定理1 对于给定 τj＞0(j=1，2，…，n)，滑动模态系统(10)是全局稳定的，如果下列条件之一成立:

1)(时滞独立)存在实矩阵P=PT＞0，H1j=，若

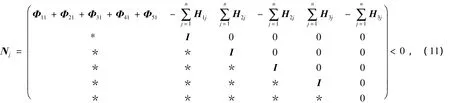
式中*为对称矩阵，并且

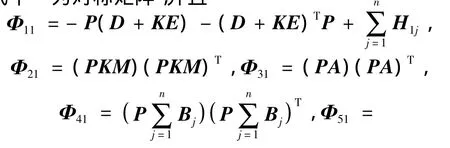
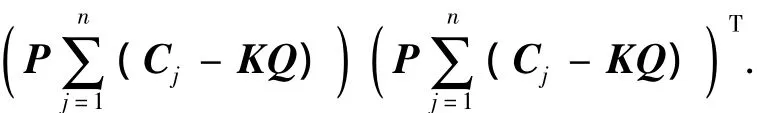
2)(时滞相关)存在实矩阵P=PT＞0，H1j=H1jT＞0，H2j=H2jT＞0，H3j=H3jT＞0，R=RT，并且r＞0，若

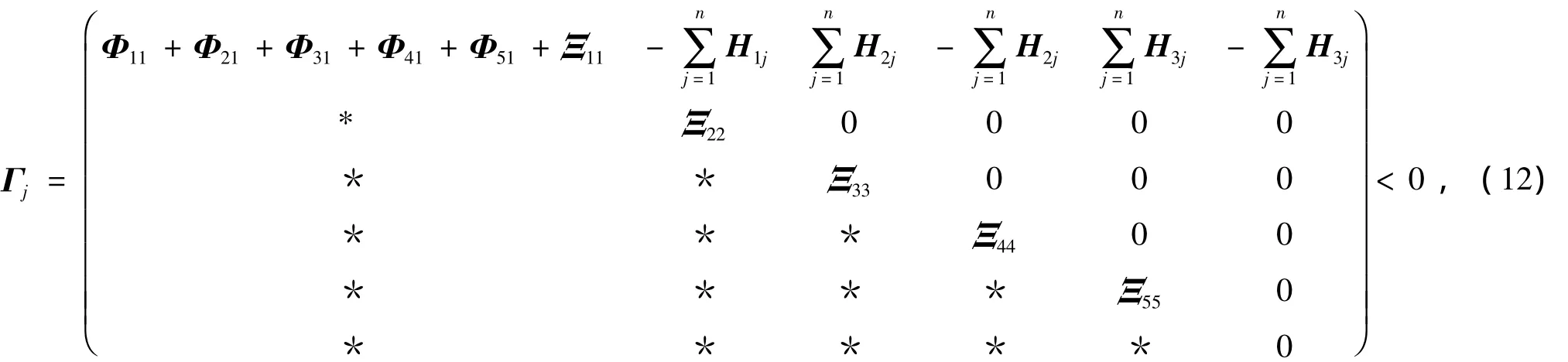
式中τj是时滞，矩阵K可分别由式(11)和式(12)得到，并且

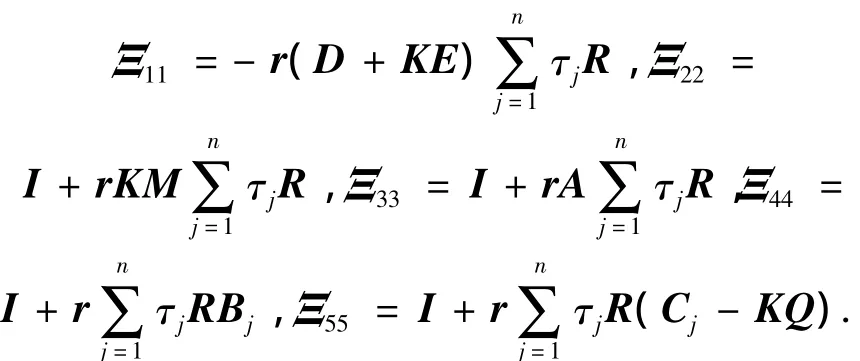
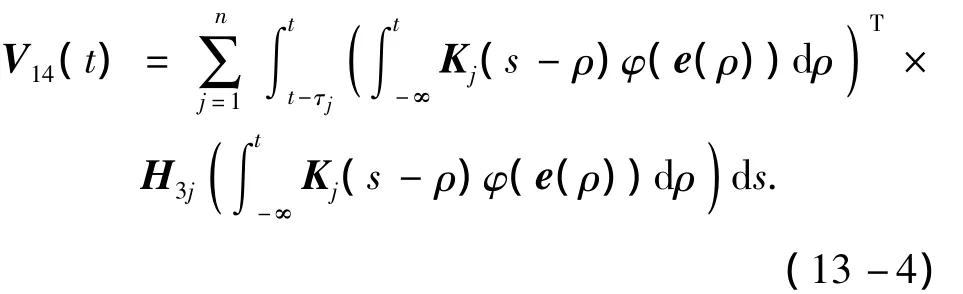
计算式(13)沿着系统(10)的导数，得到:

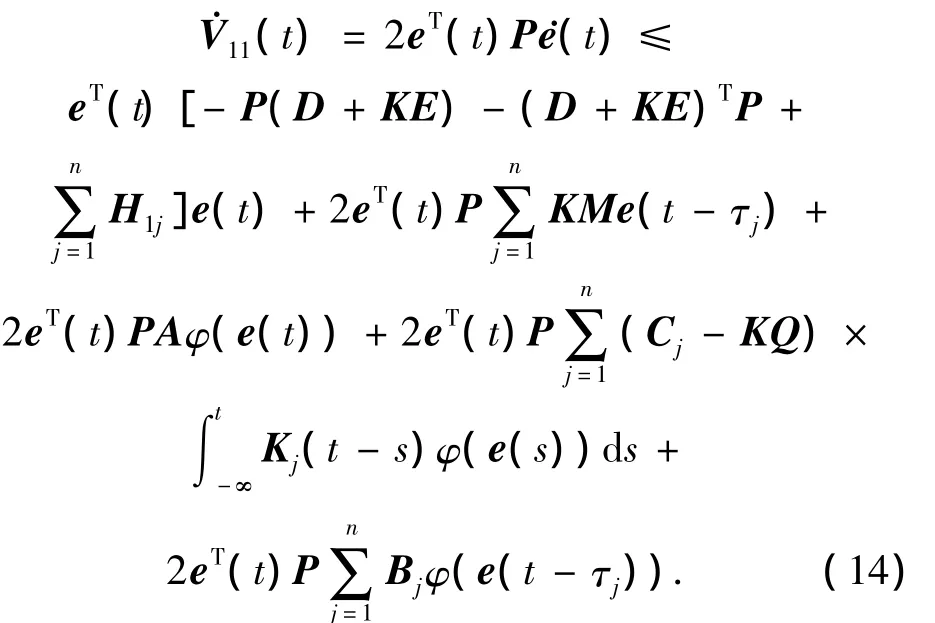
证明 首先证明系统(10)在条件(i)下全局稳定.设计Lyapunov函数:V1(t)=V11(t)+V12(t)+V13(t)+V14(t)，其中:

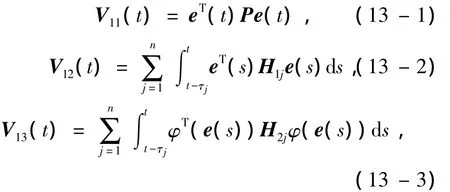
由命题1，得到:

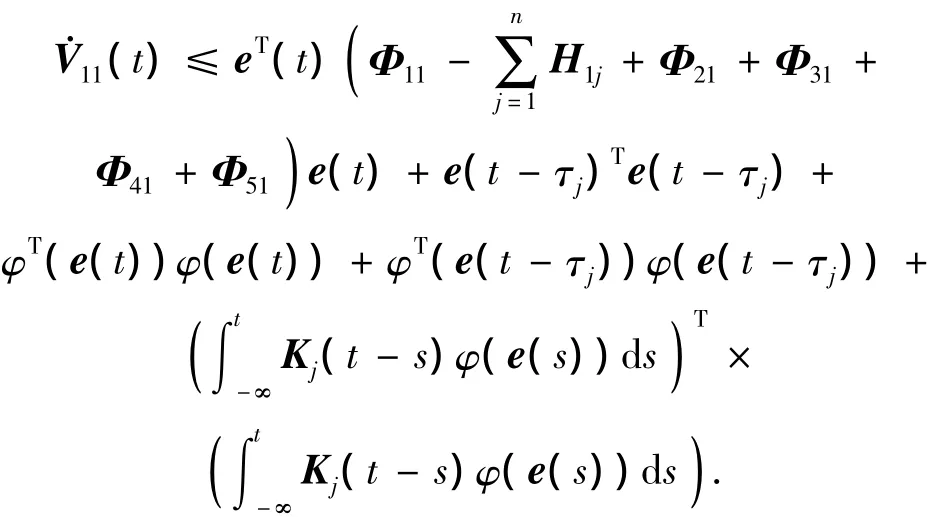
此时，取u=t-s，得

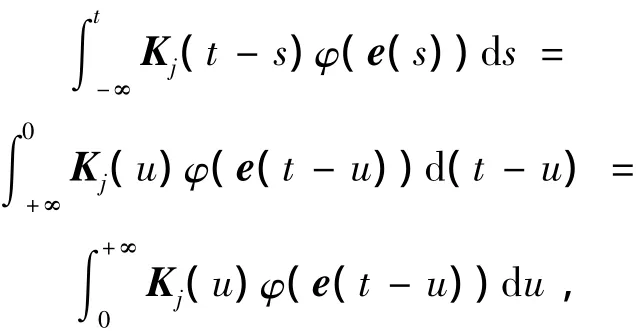
于是

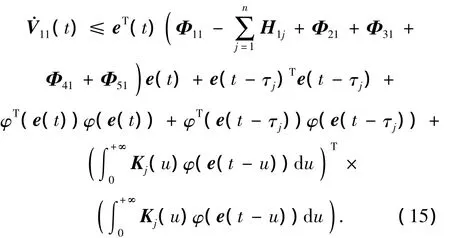
同理可得

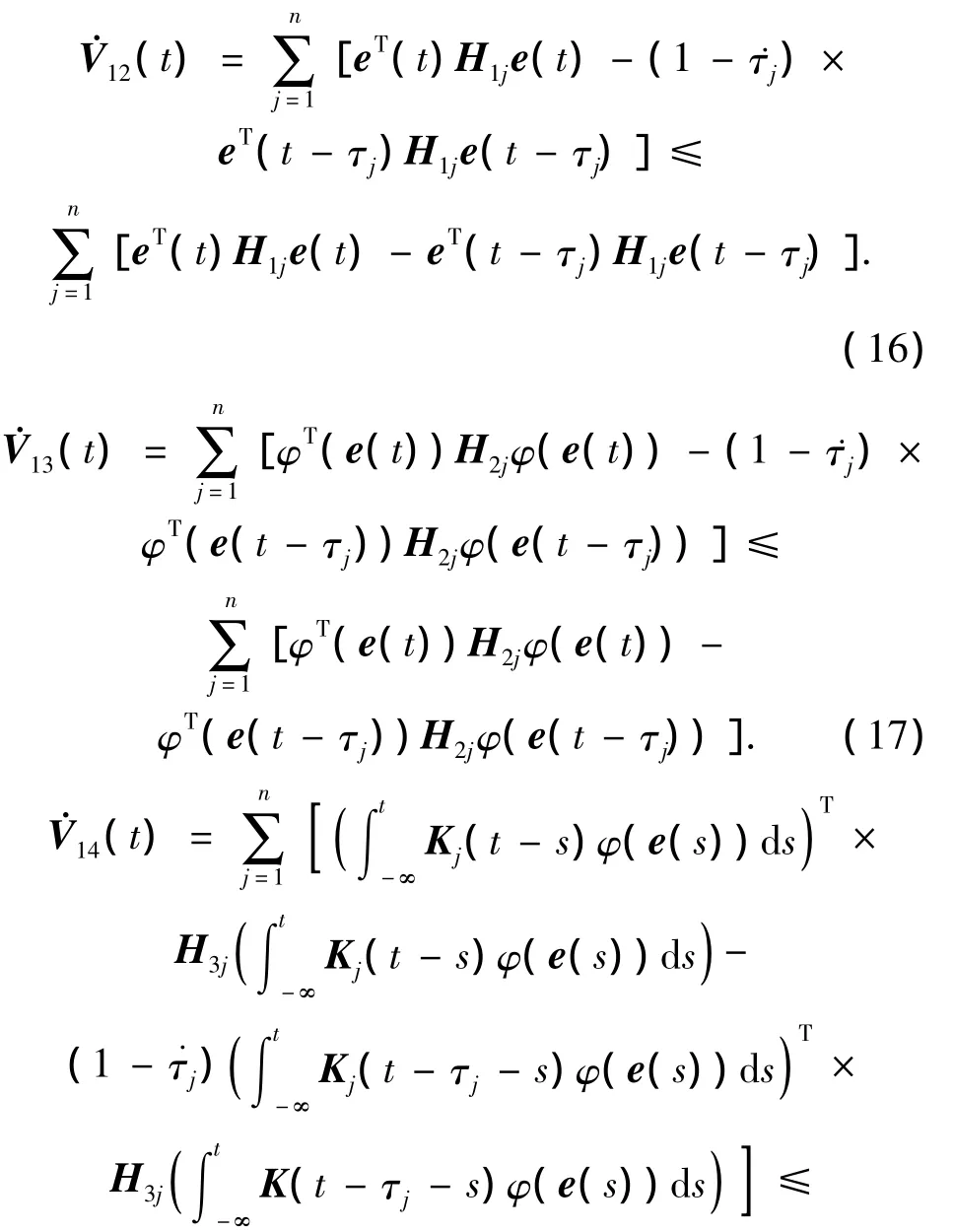
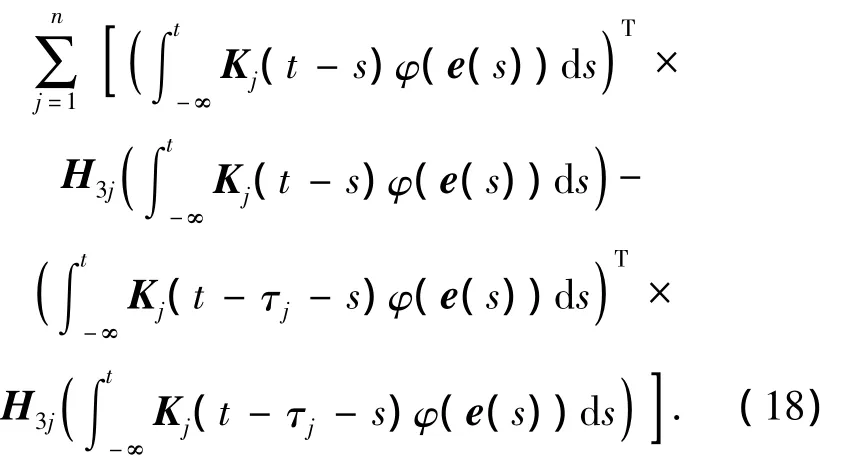
于是得到:

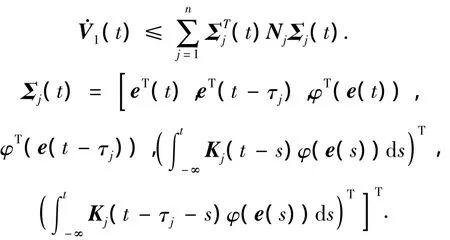
选择合适的矩阵K，再由式(11)，得

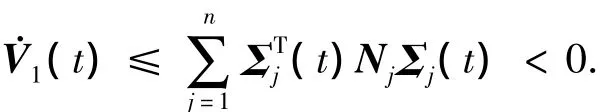
因此，在系统时滞独立的情况下，滑动模态系统(10)是全局稳定的.

对于条件(ii)，文中设计如下的Lyapunov函数:V2(t)=V11(t)+V12(t)+V13(t)+V14(t)+V15(t)，式中V11(t)，V12(t)，V13(t)，V14(t)与(13)中各项一致，并且

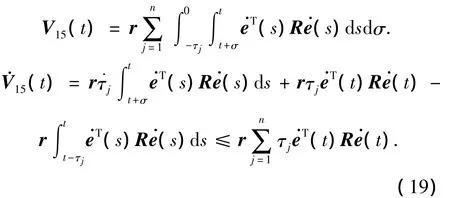
把式(15)-(19)代入系统(10)，得

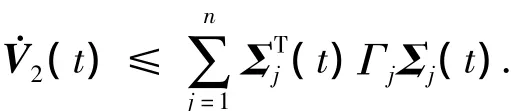
选择合适的矩阵K，再由式(12)得

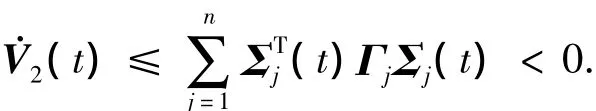
因此，在系统时滞相关情况下，滑动模态系统(10)是全局稳定的.

定理1考虑了系统(10)在时滞独立与时滞相关条件下，系统都是全局稳定的.此方法降低了保守性，在证明过程中，也运用了引理1中的命题，并且文中结果充分保证了系统(1)和系统(4)的全局同步.对比文献［9］，文中不仅解决了时滞细胞神经网络具有多时滞的问题，同时也完成了具有分布时滞问题的分析.

3 到达能力分析

为了保证所设计的滑模面满足达到条件，选择合适的滑模控制器如下:

定理2 考虑误差系统(6)，假设滑模面由(7)给定，其中P，K，r为式(11)，(12)中合适的解，若常量θ＞0，设计如下滑模控制器:

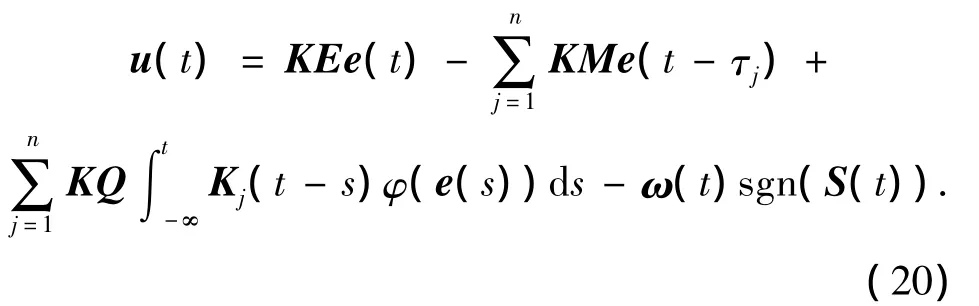
切换值ω(t)为

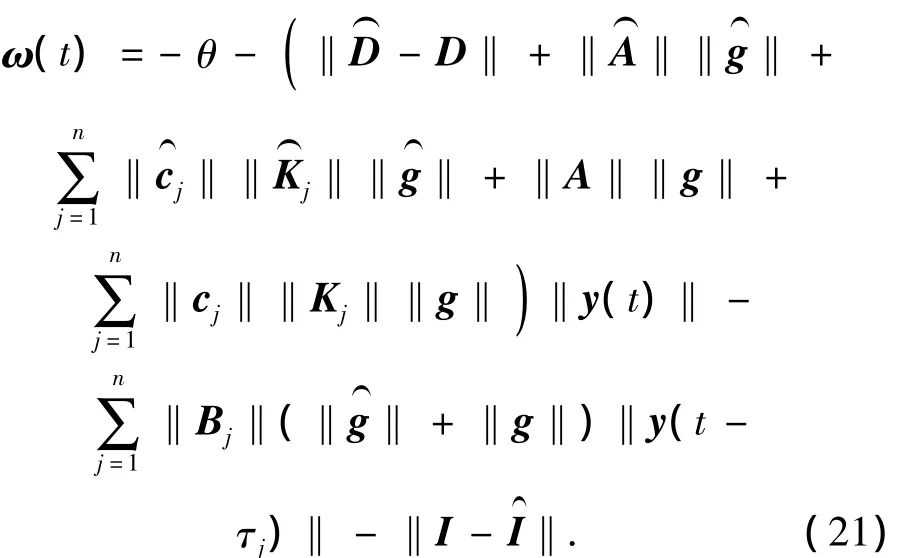
则误差系统的轨迹可以全局达到滑模面S(t)=0.

证明 为了设计合理的滑模控制器来使得滑模面满足达到条件，由式(7)和(20)，有

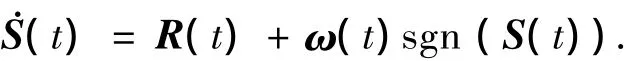
考虑如下的Lyapunov函数:

由式(21)得

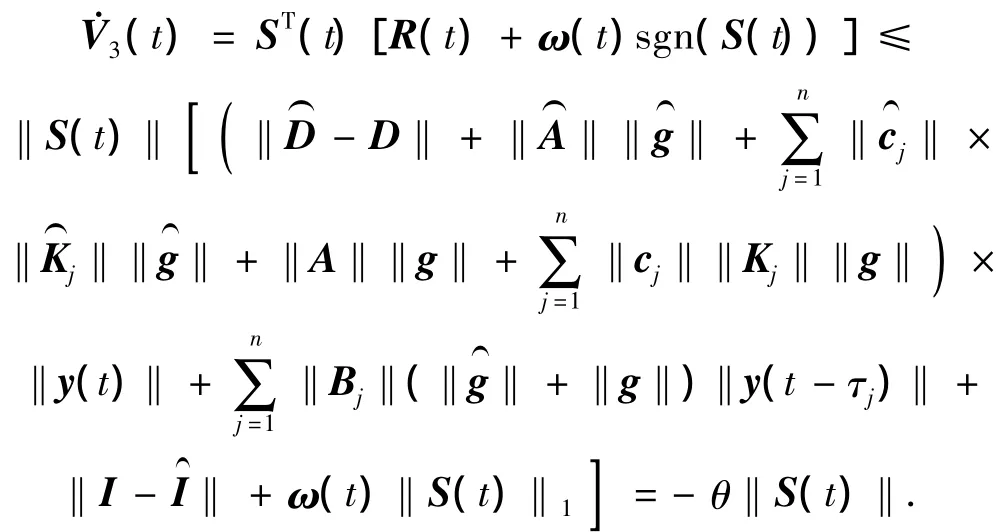
这意味着对任何S(t)≠0，都有(t)＜0.于是，误差系统(6)的轨迹全局达到滑模面并且持续保持在该平面上.因此，时滞细胞神经网络(1)与(4)达到全局同步.

文中设计的滑模控制器，可以视为由误差反馈控制输出来获得高增益补偿的准则，用以处理神经网络的全局同步问题.并且，此方法可以应用于其他复杂神经网络.

4 结论

文中研究了具有多时滞和分布时滞的细胞神经网络的全局同步问题.基于Lyapunov稳定性理论，利用线性矩阵不等式技巧化简，用改进的滑模控制方法解决了系统的全局同步问题.定理1得到了误差系统在时滞独立与时滞相关情况下全局稳定的充分条件.定理2设计的滑模控制器保证了误差系统的轨迹全局达到滑模面并且保持在该滑模面上，进而得到了具有多时滞和分布时滞细胞神经网络的全局同步.文中结果更具一般性且能更好地适应实际应用.

References)

［1］Chua Leon O，Yang Lin.Cellular neural networks:theory［J］.IEEE Transactions on Circuits and System，1988，35(10):1257-1272.

［2］Cai Guoliang，Shao Haijian.Synchronization-based approach for parameters identification in delayed chaotic network［J］.Chinese Physics B，2010，19(6)，doi:10.1088/1674-1056/19/6/060507.

［3］Yang Yongqing，Cao Jinde.Exponential synchronization of the complex dynamical networks with a coupling delay and impulsive effects［J］.Nonlinear Anal，Real World Appl，2010，11(3):1650-1659.

［4］Cai Guoliang，Yao Qin，Shao Haijian.Global synchronization of weighted cellular neural networks with timevarying coupling delays［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17(10):3843-3847.

［5］王树国，姚洪兴.拓扑结构时变的多时滞耦合供应链复杂网络的牵制控制［J］.江苏大学学报:自然科学版，2012，33(2):239-243.Wang Shuguo，Yao Hongxing.Pinning synchronization of supply chain complex networks with time-varying topological structures and multiple coupling delays［J］.Journal of Jiangsu University:Natural Science Edition，2012，33(2):239-243.(in Chinese)

［6］Cai Guoliang，Shao Haijian，Yao Qin.A linear matrix inequality approach to global synchronization of multi-delay Hopfield neural networks with parameter perturbations［J］.Chinese Journal of Physics，2012，50(1):50-63.

［7］蔡国梁，周维怀，郑 松，等.不确定离散系统全程滑模变结构控制［J］.江苏大学学报:自然科学版，2010，31(3):363-368.Cai Guoliang，Zhou Weihuai，Zheng Song，et al.Global sliding-model variable structure control for uncertain discrete-time systems［J］.Journal of Jiangsu University:Natural Science Edition，2010，31(3):363-368.(in Chinese)

［8］Huang He，Feng Gang.Synchronization of nonidentical chaotic neural networks with time delays［J］.Neural Networks，2009，22(7):869-874.

［9］Shao Haijian，Cai Guoliang，Wang Haoxiang.An linear matrix inequality approach to global synchronisation of non-parameters perturbations of multi-delay Hopfield neural network ［J］.Chinese Physics B，2010，19(11):110512.

［10］Gan Qintao，Xu Rui，Kang Xibing.Synchronization of chaotic neural networks with mixed time delays［J］.Communications in Nonlinear Science and Numerical Simulation，2011，16(2):966-974.

［11］张化光.递归时滞神经网络的综合分析与动态特性研究［M］.北京:科学出版社，2008.

［12］Cai Guoliang，Yao Qin，Fan Xinghua，et al.Adaptive projective synchronization in an array of asymmetric neural networks［J］.Journal of Computers，2012，7(8):2024-2030.