MMC的无锁相环直接功率控制仿真

段程亭，宋平岗，李云丰，江 浪，马卫东，罗善江

（华东交通大学电气与电子工程学院，江西 南昌330013）

在能源日益紧缺和环境污染等问题越来越严重的形势下，我国在新能源（风能、太阳能）等再生能源方面的投入不断扩大，但往往这些分布式能源具有分散性、远离负荷中心等特点［1］，如若采用传统的交流直流输电技术或者交流输电技术，存在很多缺陷，无法满足输电要求。基于电压源换流器的高压直流输电（voltage source converter-high voltage direct current transmission，VSC-HVDC）技术，能在可再生能源输电系统的发电互联和并网、海上孤岛和城市供电等方面发挥较好的技术优势［2］。在传统的两电平、三电平电压源换流器拓扑结构之后出现的模块化多电平变流器（modular multilevel converter，MMC）具备级联式变流器的特点，由于采用了模块化结构，容易实现多电平输出，并能在直流侧实现背靠背连接，是一种比较适用于VSC-HVDC的多电平拓扑结构［3］。MMC具有静止同步补偿器功能、无需电网支撑换相、工程建设用地和费用少等独特优点［4-10］。

目前VSC多采用电压外环电流内环的双闭环直接电流控制策略［11］，然而各种新型的控制策略也不断的被提出，直接功率控制策略［11-16］就是其中的一种，在DPC 下建立的数学模型消除了电流项，只保留了电网电压和功率以及相关系统参数。文献［12-16］研究了传统两平VSC的直接功率控制策略，由于每相只有两个状态，在SVPWM调制策略下［17］，主电路开关表非常适用。但MMC每相桥臂是由很多个子模块级联而成的，电平数较多，电压矢量数目大大增加，对换流器的控制就变得非常困难，因此开关表对于MMC来说将不再适用。

本文在αβ坐标系中推导了关于MMC的DPC数学模型，相异于以往在dq坐标系中建立控制系统不同，是在αβ坐标系中设计了无锁相环的DPC 控制系统。为了防止系统频率和电感参数变化对控制系统的干扰，设计了一种无系统角频率和电感参数的功率解耦控制器，将双闭环简化为功率单环，考虑电网强度对换流站运行特性的影响，计算出适用于直接功率控制的交流系统短路比的范围，并进行了仿真验证。

1 MMC基本原理

图1为MMC简化结构图，三相具有相同结构，图1中用一相上下桥臂结构图来表示，图中usj为交流端等效输出的第j（j=a，b，c）相电压；同理，isj为第j相电流；关于上桥臂的参数用字母“p”表示，下桥臂的参数用字母“n”表示。Rs和Ls为等效电阻和电感；ucj为MMC交流侧第j相电压；ujp和ijp为第j相上桥臂电压和电流；L0为桥臂等效电感；Kd和Rd为放电断路器和放电电阻；左下图为子模块（submodule，SM）结构图，SM由两个功率开关管（IGBT）T1和T2，两个功率二极管D1和D2，一个储能电容C组成，电容电压用uc表示，MMC上下桥臂分别由n个子模块级联而成。假设正常额定运行时投入N个，冗余备用R个［18］。

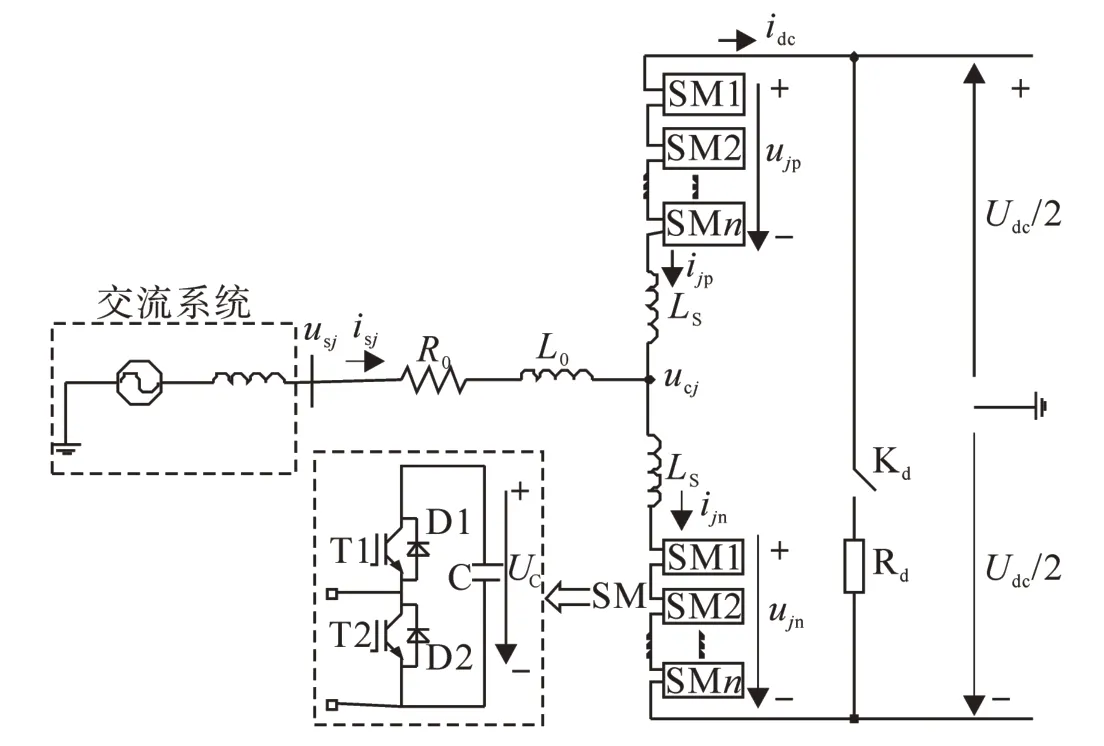
图1 MMC单相简化结构图Fig.1 Simplified structure diagram of a single phase MMC

根据基尔霍夫电压定律可得方程

式中：ujp和ijp表示第j相上下桥臂的电压总和；udc为直流端电压；ucir_jp和ucir_jn表示上下桥臂等效电感的压降。

根据基尔霍夫电流定律可得方程

式中：ijp和ijn表示j相上下桥臂电流；icirj表示第j相环流，由前面三式可推导出

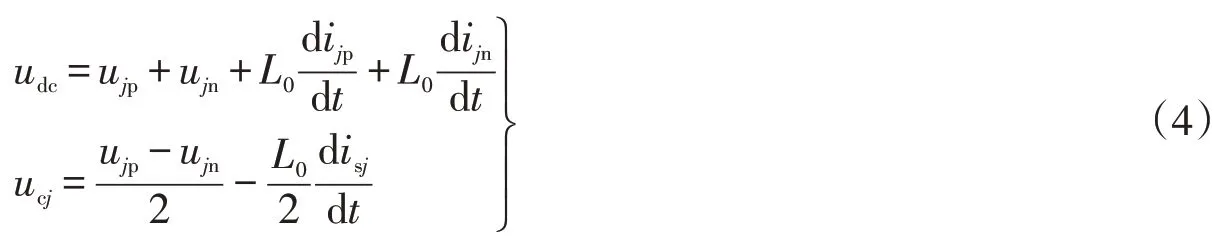
正常运行情况下，上下桥臂各投入模块数和总投入模块数满足关系

式中：njp和njn为上下桥臂投入模块数。理想情况下有［19］

式中：uc0为理想情况下电容电压值，满足uc0=udc0/N，udc0为额定直流电压额定值。通过分析可知，在相应的调制条件下改变上下桥臂投入的模块数，可得到期望的输出电压［20］。

2 数学模型描述

MMC交流侧在两相静止坐标αβ中的数学表达式为

在α轴和β轴上分别表示为

系统端电网电压基波分量可表示为

求导可得

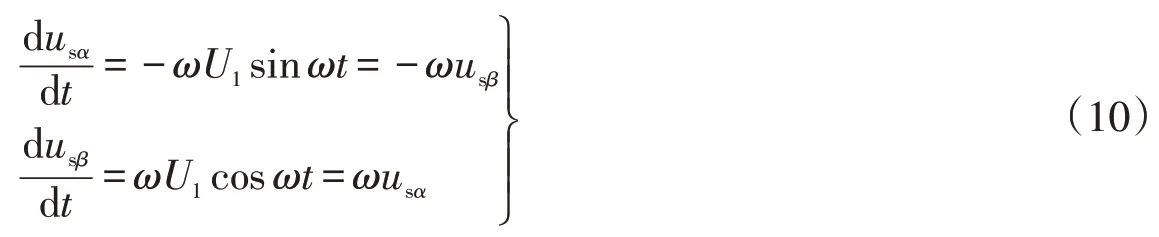
设系统参考正方向为交流电网向MMC注入功率时，反之为参考负方向，在αβ坐标系中有功功率和无功功率可表示为［21］

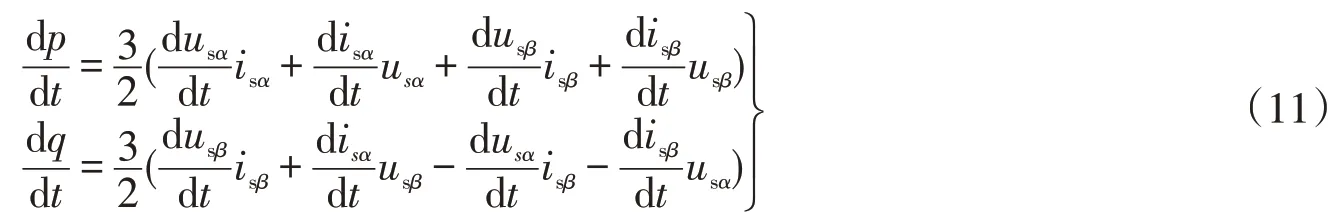
将式（8）和式（10）代入式（11）可得

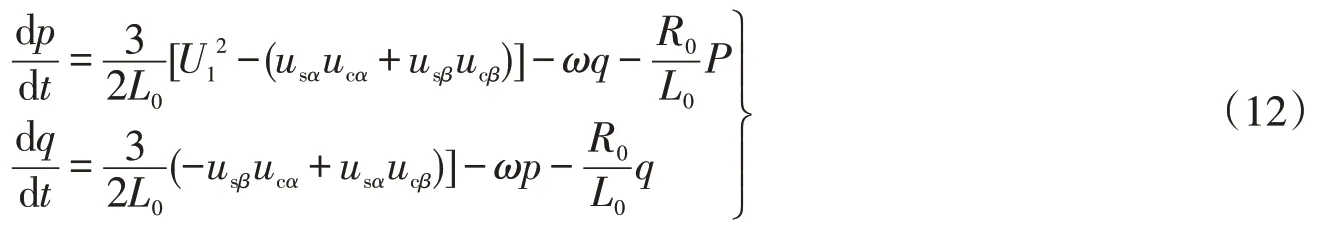
将式（12）简化成矩阵形式得

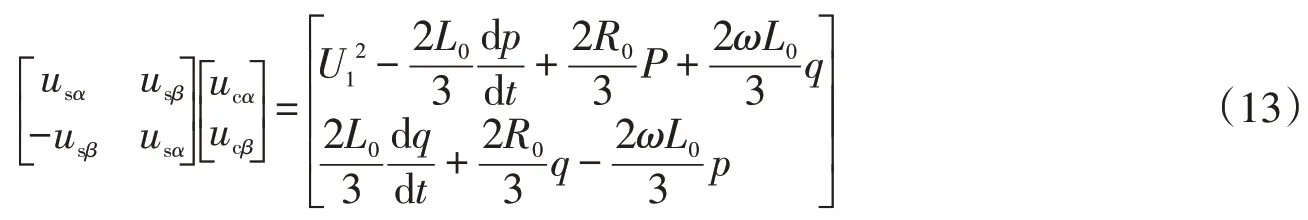
为下文研究方便，可令fp和fq表达式为

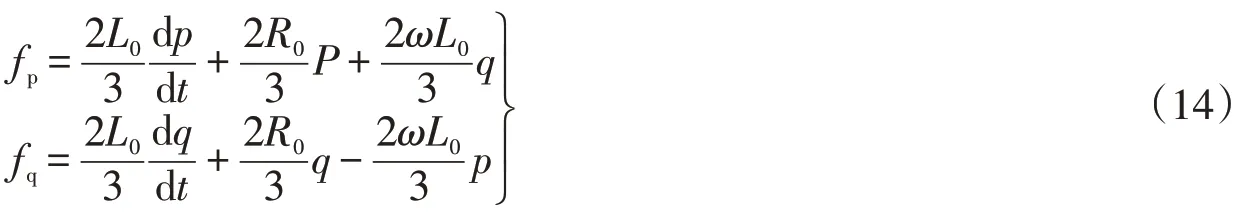
从而根据式（13）解出

从式（15）中可以得出系统电压和功率的相互关系，这有利于后面DPC控制系统的设计。传统VSC中的双闭环控制器是通过控制电流参数来控制系统功率的，本文与双环控制不同，没有采用锁相环，在直接功率控制的方式下来实现对功率在电网与MMC之间传输的控制。

3 控制器设计

3.1 DPC控制器设计

从式（14）中可以看出fp和fq是通过有功功率p和无功功率q耦合在一起，为有利于控制器的设计，需要消除其中的耦合项，实现系统有功功率和无功功率独立解耦控制。实际电路中影响等效电感L0变化的因素很多［21］，文献［19］提出了一种无电感参数的电流内环解耦控制器，经过实际验证，效果很好，但控制器中含有系统角频率ω，考虑到实际电网频率的变化，很难保证在频率不稳定的情况下系统的解耦性能。为此本文设计了无电感参数和无系统角频率参数的解耦控制器。令

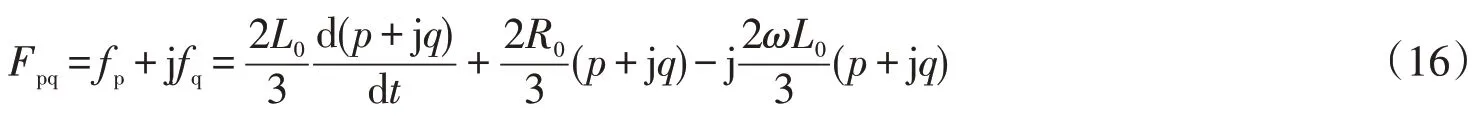
令Spq=p+jq，则上式可化为

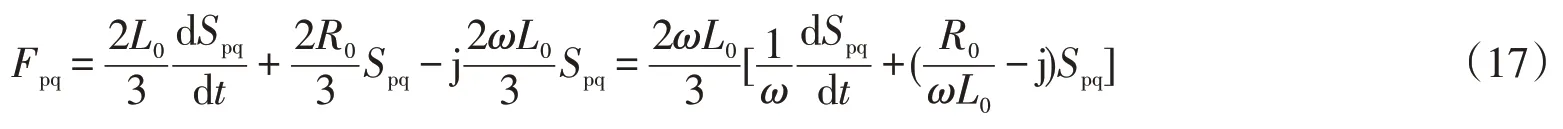
根据式（17）结构，设计无参数ω和L0的解耦控制器为

其中：kp和ki分别为比例积分控制器参数，令

式（19）中F*pq=f*p+jf*q，Serr=S*pq-Spq，S*pq=P*+jQ*。分解可得

从而可得

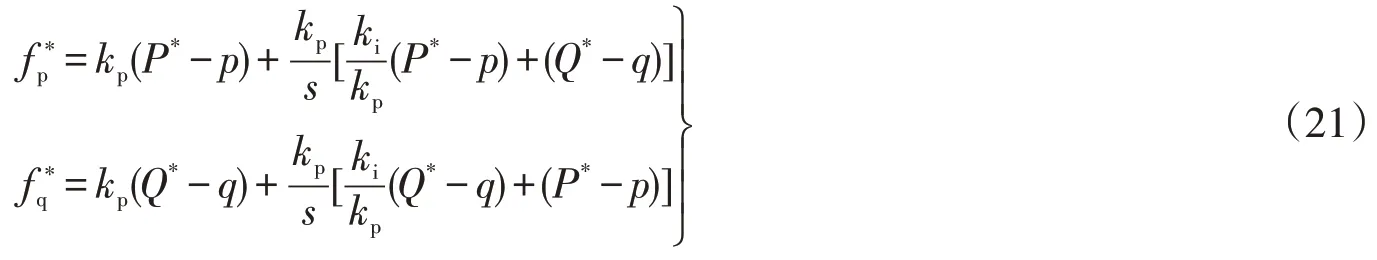
根据式（21）可设计出MMC 无系统角频率ω和无等效电感参数L0解耦控制器框图，前面已推导出了DPC的数学模型式（15），因此进一步得出电压前馈控制的模型如图2。

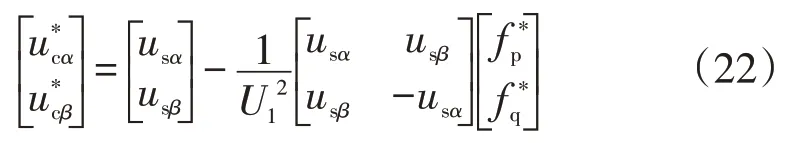
3.2 DPC控制器参数设计

控制器参数的设计和选取对于整个系统的动态稳定性能具有至关重要的意义，由于fp和fq之间存在着相互耦合，但本文所设计的控制器中无功率前馈项，因耦合的存在，很难直接求出有功功率p和无功功率q的闭环传递函数，这种情况下，可借助合成矢量来求取功率矢量闭环传递函数，理想情况下将式（22）代入式（15）可得

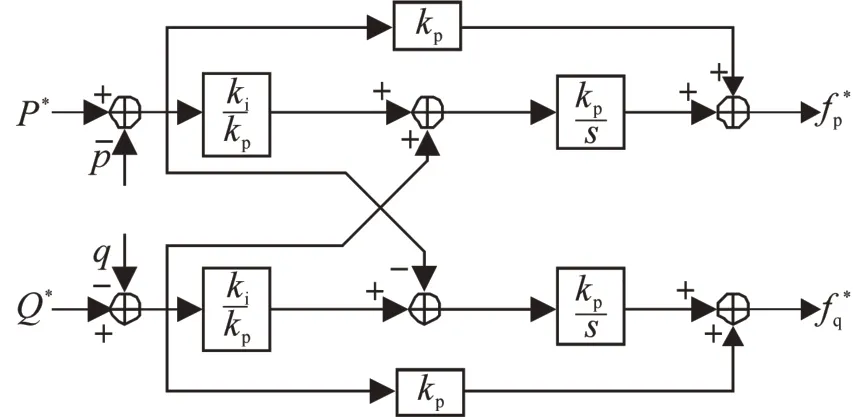
图2 无系统参数DPC控制器框图Fig.2 Control diagram without system parameters

将式（16）（19）代入式（23）可得

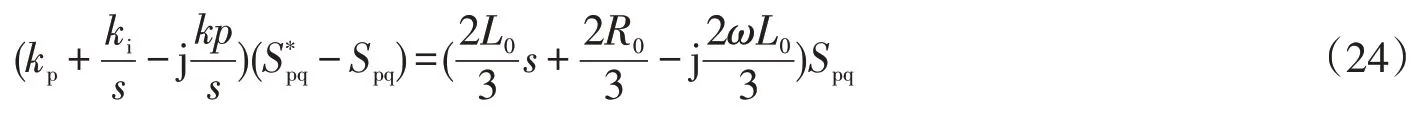
求得闭环传递函数为

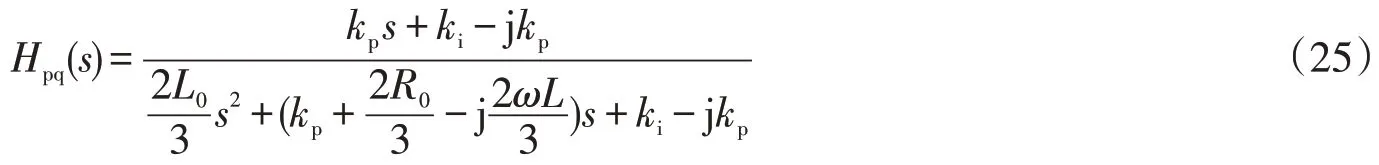
由于引入了虚数j，零极点对消的方法不适用于本文控制器的参数选取，从式（25）可观察到，当ki＞＞kp，kp＞＞R0，kp＞＞ωL0，可化简成

从而可得系统的阻尼比ξ和无阻尼振荡角频率ωξ

4 DPC适用电网强度

由于所设计的控制系统没有采用锁相环，因此建立的控制器必须要在频率发生偏移的情况下也能稳定的跟踪参考值，并且还需具有一定的谐波抑制能力。如果用理想电压源代替电网公共连接点（point of common coupling，PCC），仅仅注入一定量谐波和基波频率偏移不能完全模拟实际电网，这种情况下短路比SCR（short circnit ratio）极大，电网强度极大，但向弱电网（SCR＜3）供电时需要增大控制器参数消除频率偏移的影响，考虑到弱电网PCC处因无功变化导致的交流电压幅值变化，因此，为了维持PCC处交流电压的稳定，在电网无功功率波动很大的情况下，采用定有功功率和定无功功率组合可能不太适合向电网强度较弱的电网供电，可能导致PCC处过电压、换流器进入非线性调制区以及系统的稳定性问题，必然会增加设计运行成本。下面简单推导定有功功率和定无功功率的直接功率控制策略适用于交流系统短路比范围。

按照图3所示功率的参考方向，Rg+jXg表示线路等效阻抗，变压器变比为1∶k，R0+jX0表示变压器和链接电抗器的等效阻抗，为等效电源额定电压，为PCC 处电压，为换流器输出交流电压，以上3个电压都为相电压有效值，以下所有量的下标N都表示额定值。在高压线路中，一般电阻往往远小于电抗，同时忽略线路电阻和变压器的功率损耗，即传递至电网的功率等于换流站输出的功率。令=UgN∠0，ΔPg=Pg-PgN，ΔQg=Qg-QgN，忽略横向压降，可得线路在额定功率时阻抗产生的纵向压降

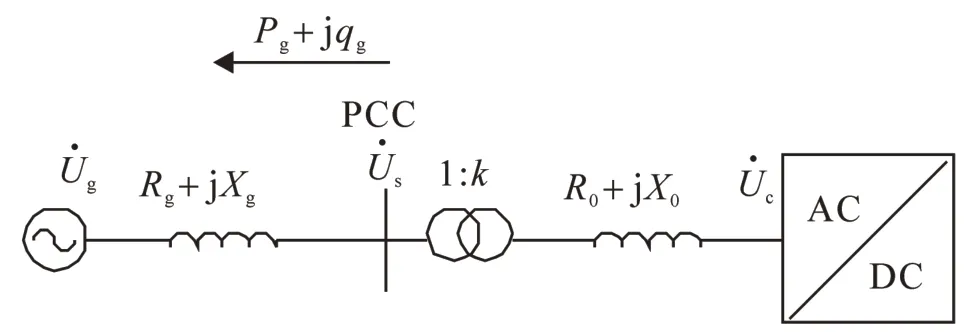
图3 MMC-HVDC单站等效电路Fig.3 Single-station equivalent circuit of MMC-HVDC

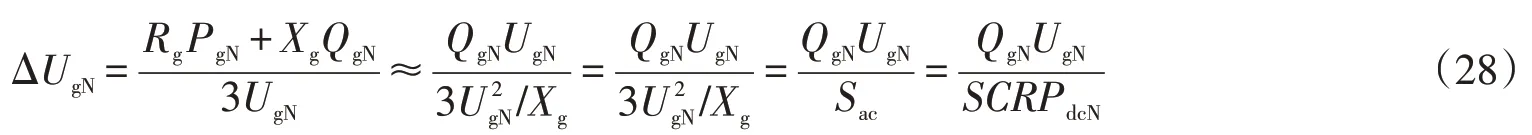
式中：Sac为PCC 处短路容量；SCR为短路比；PdcN为额定有功功率。因此，通过式（28）可估计PCC 处额定电压大约为

那么，由有功功率和无功功率波动产生的电压波动为

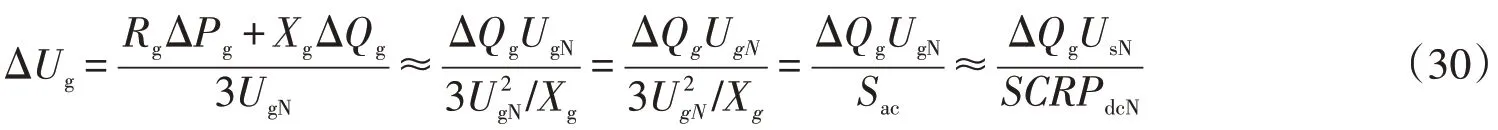
则可计算出电压波动比为

式（31）中假设ε为最大电压允许波动系数。从而，可得

根据式（31）可大致估计PCC处交流电压有效值Us为

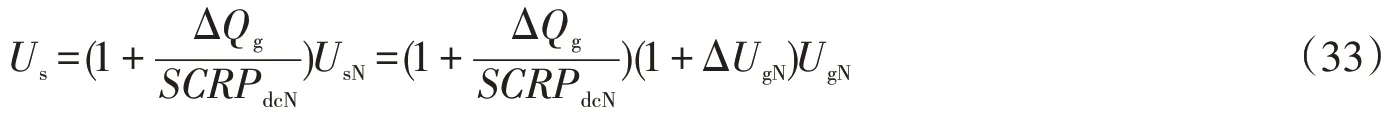
因为换流变压器采用的是YD11接法，因此，变压器二次侧对地相电压大约为kUs，不妨令变压器二次电压为kUs∠0，同时忽略阻抗上的功率损耗，即传递至电网的功率等于换流器输出的功率，于是可得换流站等效阻抗上因功率波动产生的电压波动大约为

因此换流器输出的相电压有效值可估算为

正常运行时，为了使换流器工作在线性调制范围内，避免进入非线性调制区引起的低次谐波，根据调制度的定义，换流器输出基波相电压幅值需小于直流电压的一半，即

将式（33）（35）代入式（36），可大致推算得到短路比范围为

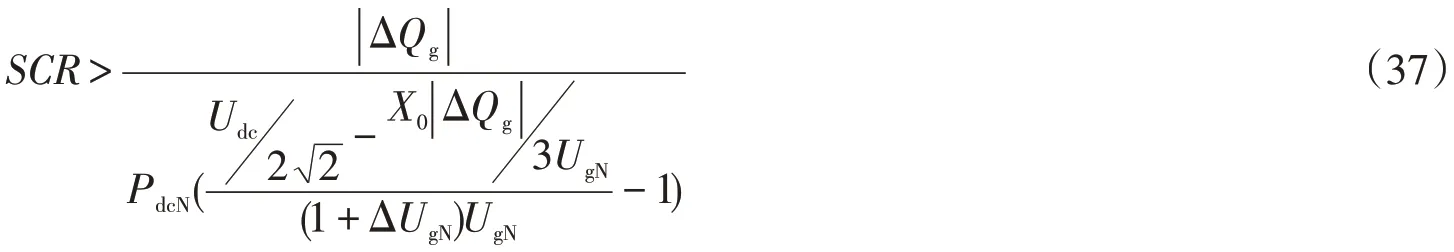
因此，按照换流器向交流系统输送有功和无功功率时设计PCC额定电压时，采用本文设计的直接功率控制策略，交流系统短路比需满足，式（32）和（37）中的最大者，一般情况下，只要直流电压足够高就不会出现因无功波动造成电压波动而使换流器进入非线性调制区。

5 仿真验证

本文在MATLAB/Simulink中搭建交流系统互联的MMC-HVDC仿真模型验证所设计的MMC无锁相环直接功率控制的正确性，子模块数20个，电源线电压10.5 kV，有功功率为12 MW，无功功率为6 Mvar，变压器容量15 MVA，变压器阻抗标幺值0.05/0.08，字模块电容20 mF。强电网线路等效电抗80 mH，接近弱电网线路等效电抗4 mH。

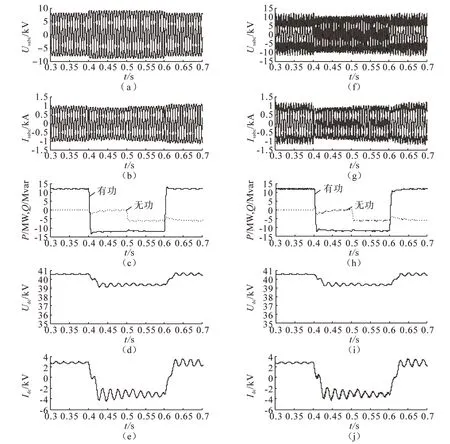
图4 强弱电网下MMC仿真波形Fig.4 Simulation waves of MMC in strong and weak grid

图4为本文提出的无锁相环直接功率控制策略在强电网下和接近弱电网下的仿真结果图。（a）（b）为图3中PCC处交流电压和交流电流波形图，0.4 s有功功率由12 MW变为-12 MW时，PCC处的交流电压幅值会适当的上升，交流电压幅值会变小。0.5 s时无功功率由零变为-6 Mvar，交流电网接收感性无功功率，此时电压幅值会进一步升高些，但波动的幅值很小，而交流电流幅值也会适当升高。（c）为有功功率和无功功率动态变化曲线，（d）和（e）图分别表示直流侧电压和电流的变化，有功率变化时直流电压和直流电流都减小，无功功率变化时直流电压和直流电流会相应增加，波动幅值会减小。图4右边为接近弱电网时仿真的效果明显不够理想，电压电流的畸变率成倍增加，完全弱电网时，系统则不能够稳定的运行。

6 结论

1）针对模块化多电平换流器的拓扑结构提出一种新型无锁相环直接功率控制方法，控制系统设计没有采用锁相环，功率解耦控制器无系统角频率和电感参数，将传统的双闭环简化为单一的功率单环，有效简化了控制系统，避免了因系统频率和电感等参数带来的不良干扰，提高了系统的稳定性。

2）为充分考虑实际电网的强弱对换流器的影响，在电网强度较弱的情况下直接功率控制方法并不适用，推导计算了适用于直接功率控制的交流电网的强度范围。

[1]宋平岗,李云丰,王立娜,等.基于微分平坦理论的模块化多电平换流器控制器设计[J].电网技术,2013,37(12):3475-3481.

[2]李云丰,宋平岗,王立娜.模块化多电平换流器无锁相环控制策略[J].电测与仪表,2014(5):56-60.

[3]王国强,王志新,李爽.模块化多电平变流器的直接功率控制仿真研究[J].中国电机工程学报,2012(6):64-71.

[4]王姗姗,周孝信,汤广福,等.模块化多电平换流器HVDC直流双极短路子模块过电流分析[J].中国电机工程学报,2011(1):1-7.

[5]韦延方,卫志农,孙国强,等.适用于电压源换流器型高压直流输电的模块化多电平换流器最新研究进展[J].高电压技术,2012(5):1243-1252.

[6]赵昕,赵成勇,李广凯,等.采用载波移相技术的模块化多电平换流器电容电压平衡控制[J].中国电机工程学报,2011(21):48-55.

[7]王姗姗,周孝信,汤广福,等.模块化多电平电压源换流器的数学模型[J].中国电机工程学报,2011(24):1-8.

[8]孔明,邱宇峰,贺之渊,等.模块化多电平式柔性直流输电换流器的预充电控制策略[J].电网技术,2011(11):67-73.

[9]TU QINGRUI,ZHENG XU,XU LIE.Reduced switching-frequency modulation and circulating current suppres-sion for modular multilevel converters[J].IEEE Transactions on Power Delivery,2011,26(3):2009-2017.

[10]ROHNER S,BERNET S,HILLER M,et al.Modulation,losses,and semiconductor requirements of modular-multilevel converters[J].IEEE Transactions on Industrial Electronics,2010,57(8):2633-2642.

[11]陈海荣.交流系统故障时VSC-HVDC系统的控制与保护策略研究[D].杭州:浙江大学,2007.

[12]NOGUCHI T, TOMIKI H, KONDO S, et al. Direct power control of PWM converter without power-source-voltage sensors[J].IEEE Transactions on Industry Applications,1998,34(3):473-479.

[13]邱大强,李群湛,南晓强.电网不对称故障下VSC-HVDC系统的直接功率控制[J].高电压技术,2012(4):1012-1018.

[14]杨兴武,姜建国.电压型PWM整流器预测直接功率控制[J].中国电机工程学报,2011(3):34-39.

[15]何致远,韦巍.基于虚拟磁链的PWM整流器直接功率控制研究[J].浙江大学学报:工学版,2004(12):86-89.

[16]陈伟,邹旭东,唐健,等.三相电压型PWM整流器直接功率控制调制机制[J].中国电机工程学报,2010(3):35-41.

[17]陈诚,王勋,程宏波.三相PWM整流系统研究[J].华东交通大学学报,2012,29(6):40-44.

[18]李云丰,宋平岗,王立娜,等.一种模块化多电平换流器数学模型的建立方法[J].华东交通大学学报,2013,30(2):37-41.

[19]汤广福.基于电压源换流器的高压直流输电技术[M].北京:中国电力出版社,2009:88-106.

[20]LI ZIXIN, PING WANG, ZHU HAIBIN, et al. An improved pulse width modulation method for Chopper-Cell-Based modular multilevel converters[J].IEEE Transactions on Power Electronics,2012,27(8):3472-3481.

[21]王恩德,黄声华.三相电压型PWM整流的新型双闭环控制策略[J].中国电机工程学报,2012(15):24-30+8.