基于故障阻抗计算的非同步故障测距新方法
2014-12-22傅军栋樊海全
傅军栋,李 澄,王 锴,樊海全
(华东交通大学电气与电子工程学院,江西 南昌330013)
在电力系统中,担负电能输送任务的高压输电线路发生故障最多,快速准确的故障定位对系统安全稳定和经济运行十分重要。在电力工程界,输电线路故障定位装置的出现不但减轻了人工巡线劳动强度,而且使得测距更加精准[1],在电力牵引网贯通线[2-4]中还存在故障测距适应性问题。因此,对故障测距领域进行更加快速、准确、灵活等方面的研究具有重要的实际意义。
输电线路短路故障常有发生,考虑到电力系统运行方式变化及过渡电阻的存在会对单端量测距结果影响较大,文章主要研究在原理上不受上述影响的双端量测距。双端量法需要用到两侧的数据[5],广域测量系统中的PMU(phasor measurement unit,相量测量单元)可以提供两侧同步数据。然而,PMU优化配置满足状态观测时可实现对全网的动态实时监控,即并非在全网所有厂站、母线都配置该装置,且考虑到装置失灵时必然存在两端数据非同步,产生测距误差。
迄今为止,国内外学者提出的双端数据测量非同步的故障测距方法有限,主要有构造非线性方程[6-8]、估算非同步角[9]、消去不同步角[10]的3种方法。考虑到求解非线性方程时采用的迭代法收敛性和估算非同步角时估算误差均具有不确定性问题,消去非同步角法就成了最有效可靠的方法。因此,主要研究如何消去非同步角来实现故障测距。
采用输电线路集中参数模型,提出了基于故障阻抗计算的非同步故障测距新方法。该方法首先利用双端电气量求故障导纳和故障阻抗,使得故障阻抗表达式中仅含故障距离一个未知量,并且在计算过程中巧妙地消去了非同步角影响,然后基于金属性短路故障阻抗的纯电阻性采用共轭法构造出以故障距离为未知量的一元二次方程,最后给出了伪根的判别方法,求解方程即完成测距。仿真结果表明该方法简单易行,测距精度高,不受非同步角的影响,能适用于各种故障类型,鲁棒性好[11]。
1 原理
1.1 线路模型
用单线图表示经完全换位的单回输电线路,线路发生单相接地短路故障如图1所示。以母线S,R为始末端的线路全长为l,线路采用集中参数模型,单位长度阻抗为Z。两端母线电压和电流分别为US,IS和UR,IR,故障点F距离始端S距离为d,故障阻抗为ZF。
对于集中参数模型的输电线路,依据电路基本原理,从始端S推算至故障点F的电压UFS和末端R推算至故障点F的电压UFR分别为

1.2 非同步电气量校正
通常情况下,电气量测量非同步是指测量装置的时钟误差,误差由装置本身固有的缺陷而产生。双端量法故障测距需要用到两端的电压、电流数据。在电气量测量非同步时,利用这些数据进行计算得到的测距结果误差较大,所以出于测距精度的考虑就必须对非同步电气量进行校正。以始端时钟为参考时刻,末端母线电压和电流皆因非同步测量而变化,而线路单位长度阻抗Z和长度l则与之无关。以下对末端非同步测量的电压和电流进行校正,记末端R侧时钟相对于始端S侧时钟的偏差为t,则非同步角δ=2πt/40=πt/20(40表示采样频率为2 kHz时一个周期的采样点数)。由于δ=0就是同步测距的情况,因此非同步测距必然适用于同步测距。于是,校正后的末端R侧的电压和电流为

此时,校正后的从末端R侧推算至故障点F的电压为
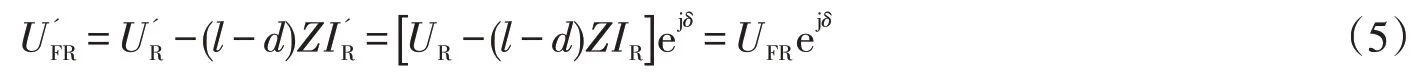
依据电路基本原理可知,从始端S侧推算至故障点F的电压UFS与校正后的从末端R侧推算至故障点F的电压相等,且都等于故障点电压UF;从始端S侧流入故障点F的电流IS与校正后的从末端R侧流入故障点F的电流之和为故障电流IF:

1.3 故障阻抗计算
故障阻抗就是在故障点处故障相导线与地之间或者几个故障相导线间发生的非正常连接的阻抗,可依据欧姆定律计算故障阻抗ZF。在故障点F处,由故障点电压UF和故障电流IF可推得故障导纳YF:

将(6)(7)代入上式,并结合(4)(5)可得(9):
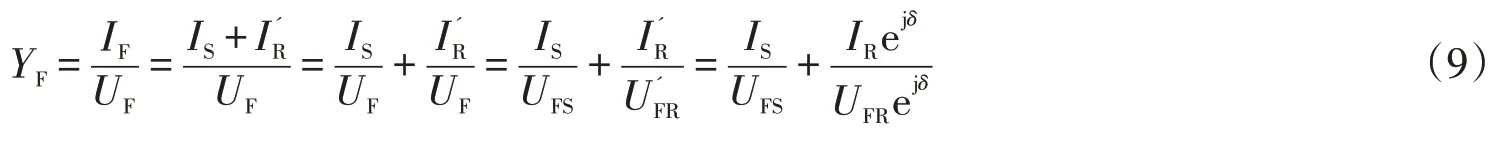
在电路分析中,用阻抗或导纳表示欧姆定律是一种普遍形式。注意到阻抗和导纳互为倒数,可由ZFYF=1得故障阻抗ZF:
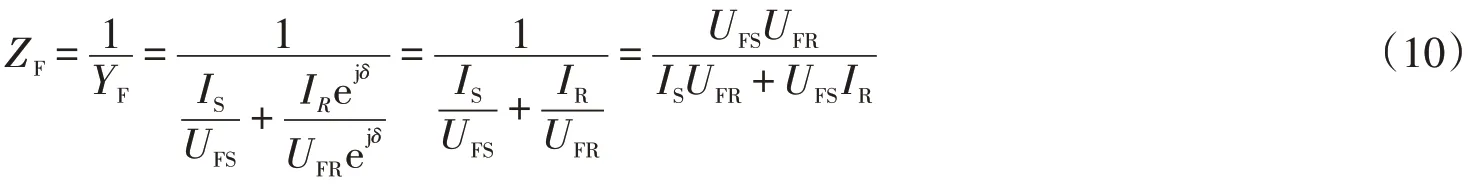
上式中ejδ≠0 恒成立,对ejδ的约分消除步骤有意义。从右端分式中看出故障阻抗计算表达式中不含ejδ,消除了非同步角的影响,因此(10)式可方便地用于非同步故障测距分析。故障阻抗计算表达式为分式,分别定义故障阻抗计算分子Q和故障阻抗计算分母W:

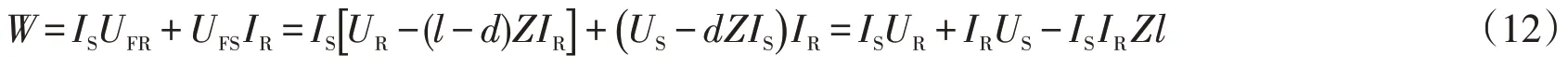
式中:Q的表达式系数A,B,C分别为:A=-Z2IRIS,B=USZIR-URZIS+Z2ISIRl,C=US(UR-ZIRl)。
从(11)和(12)可见,当双端电气量和线路基本参数一定时,Q是d的二次函数,W是常数。因此,故障阻抗ZF可以写成(13):

1.4 共轭法构造方程求d
系统中电气量大部分用相量表示,而复数是相量分析方法的基础,复数的代数形式为f=a+jb(其中,j=为虚单位,复数f的实部a=Re[f],虚部b=Im[f]),其共轭复数为f*=a-jb。共轭法就是对方程等式两边同时取共轭复数形式以得到新的方程。发生短路故障时,故障阻抗通常情况为纯电阻,其复数阻抗的虚部为零。对(13)两边取共轭复数,此时有故障阻抗的共轭复数与故障阻抗相等,即=ZF,则有(14):
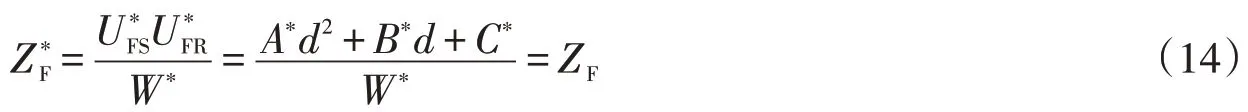
式中:W*为故障阻抗计算分母W的共轭复数;为UFS的共轭复数;为UFR的共轭复数;A*,B*,C*分别为故障阻抗计算分子Q的表达式系数A,B,C的共轭复数。
考虑到W和W*不为零,为不失一般性,联立(13)(14)消去ZF,写成适用于非零W和W*形式情况,即W*UFSUFR=,整理得(15):

其中:
p=W*A-WA*;
q=W*B-WB*;
r=W*C-WC*;
A*=-Z*Z*;
B*=;
C*=;
W*=。
显然p≠0 恒成立,方程(15)的解为

因此,仅需确定一元二次方程的各项系数p,q,r,就可以求得故障距离d,这里存在两个解d1和d2,需要去除伪根。
1.5 伪根识别
首先注意到输电线路的长度为l,其故障距离d必然满足(17):

其次,将解得的两个解d1和d2分别代入(13)计算,可得到相对应的故障阻抗计算ZF1和ZF2,而实际故障阻抗值为ZF。虽然测量计算中不可避免的误差会使计算值与实际值之间存在误差,但是误差不会太大。真实故障距离对应的故障阻抗计算值必然与实际值更为接近,故障阻抗计算值必然满足(18):

由(18)得到对应的两个解d1和d2之一即为真根。至此,采用(17)(18)进行判别即可方便地去除伪根。
2 算法实现
采用包含于各种短路故障中的正序分量进行计算。因为线路两端母线电压和电流获取容易,所以在线路参数已知时由前述原理可方便地确定一元二次方程的系数,进而求解方程实现测距。于是,测距差Δd=d-dS,测距误差Δ:

式中:d为计算故障距离;dS为实际故障距离;l为线路全长。
至此,故障阻抗计算法的故障测距算法步骤如下:
1)开始;
2)输入线路参数和长度l;
3)确定线路单位长度阻抗Z、始端电压US、始端电流IS、末端电压UR、末端电流IR及各自的共轭复数值Z*,,,,;按照式(11)计算故障阻抗分子Q的表达式系数A,B,C及其共轭复数值A*,B*,C*;按照式(12)计算故障阻抗分母W及其共轭复数值W*;
4)由步骤3中确定的各值计算一元二次方程方程(15)中的系数p,q,r并依据(16)计算故障距离d1,2;
5)按照(17)(18)判别伪根后得到故障距离真根d;
6)按照式(19)计算测距误差Δ;
7)输出故障距离d和测距误差Δ;
8)结束。
3 仿真验证
为验证所提出的非同步测距新方法,参照双端系统模型(如图2),在PSCAD中搭建一条长为120 km的500 kV 的三相单回输电线路进行仿真分析。表1 和表2 分别为系统参数和赣洪都—赣州500 kV 线路基本参数。

图2 双端系统模型Fig.2 Model of two-end system

表1 系统参数Tab.1 System parameters
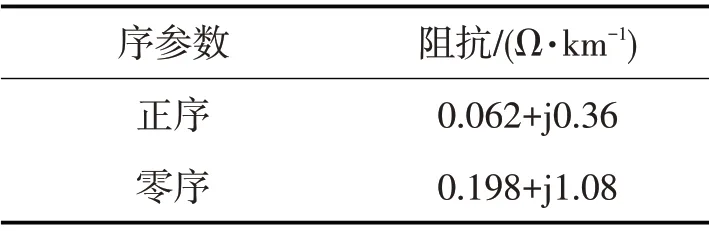
表2 输电线路参数Tab.2 Transmission line parameters
3.1 单相接地短路故障测距
线路A相接地短路故障发生时刻为0.3 s,故障时延0.1 s。两侧系统中性点接点,故障电阻为10 Ω。仿真采样频率为2 kHz,利用故障后50 ms之内的数据进行测距计算。由于故障相两侧电压和电流中含有基波、谐波分量和衰减直流分量,因此为克服衰减直流分量以及谐波分量的影响,采用测距精度较高的差分傅氏滤波算法进行滤波,由滤波后的数据按照对称分量法计算各正序分量。最后,利用MATLAB按照本文提出的故障阻抗计算法进行编程与计算,即可求得故障距离d和误差Δ。
3.1.1 非同步角对测距结果的影响
为了考察非同步角δ对测距结果的影响,当线路上不同地点发生单相接地短路故障时,计算出当δ在-180°到180°之间变化时采用故障阻抗计算法的测距结果(见表3)。
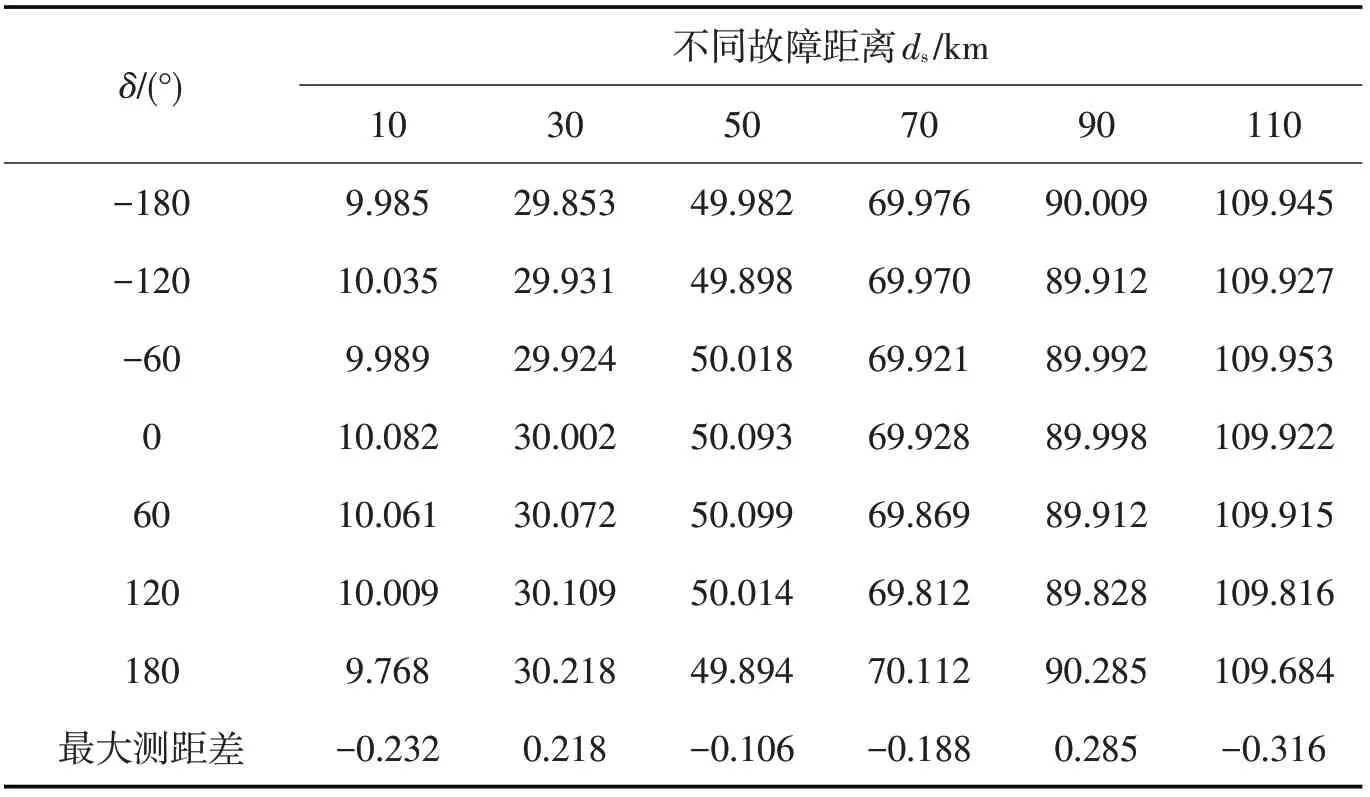
表3 非同步角对测距结果的影响Tab.3 The effect of unsynchronized angle to fault location result
从表3可以看出,120 km长的线路在10 km到110 km之间发生故障的最大测距差为-0.316 km,越靠近线路中间点时测距差越小,最小测距差为-0.106 km,非同步角δ对新方法测距结果影响甚微。
3.1.2 故障电阻对测距结果的影响
选取当δ=60°时线路不同故障距离dS发生单相接地短路故障,不同故障电阻Rg对应的测距结果如表4 所示。从表中可以看出,当故障电阻从100 Ω至500 Ω变化时,最大与最小测距差分别为0.210 km 与0.034 km,可见故障电阻对测距结果几乎没有影响。
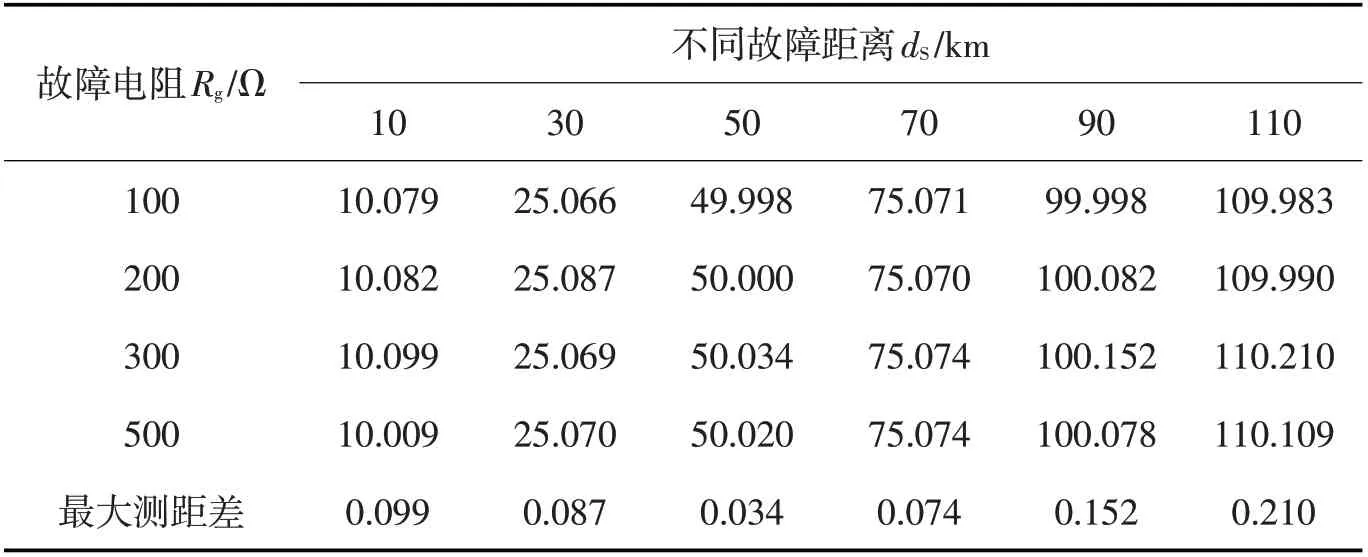
表4 不同故障电阻对测距结果的影响Tab.4 The effect of different fault resistance to fault location result
3.2 不同短路故障类型测距
参照前述单相接地故障测距步骤,分别对两相接地、两相短路、三相短路情况采用新方法进行计算。图3 给出了对应于各短路故障在不同非同步角δ和不同故障距离dS的测距误差Δ情况。从图中可以看出,越靠近线路中点测距误差越小,越靠近两侧误差越大。从图3(a)可以看出,单相接地短路最大测距误差不超过0.27%;从图3(b)可以看出,两相接地短路最大测距误差不超过0.5%;从图3(c)可以看出,两相短路最大测距误差不超过0.5%;从图3(d)可以看出,三相短路最大测距误差不超过0.25%。由此可知三相短路测距误差最小,新方法可以适用于各种短路故障。
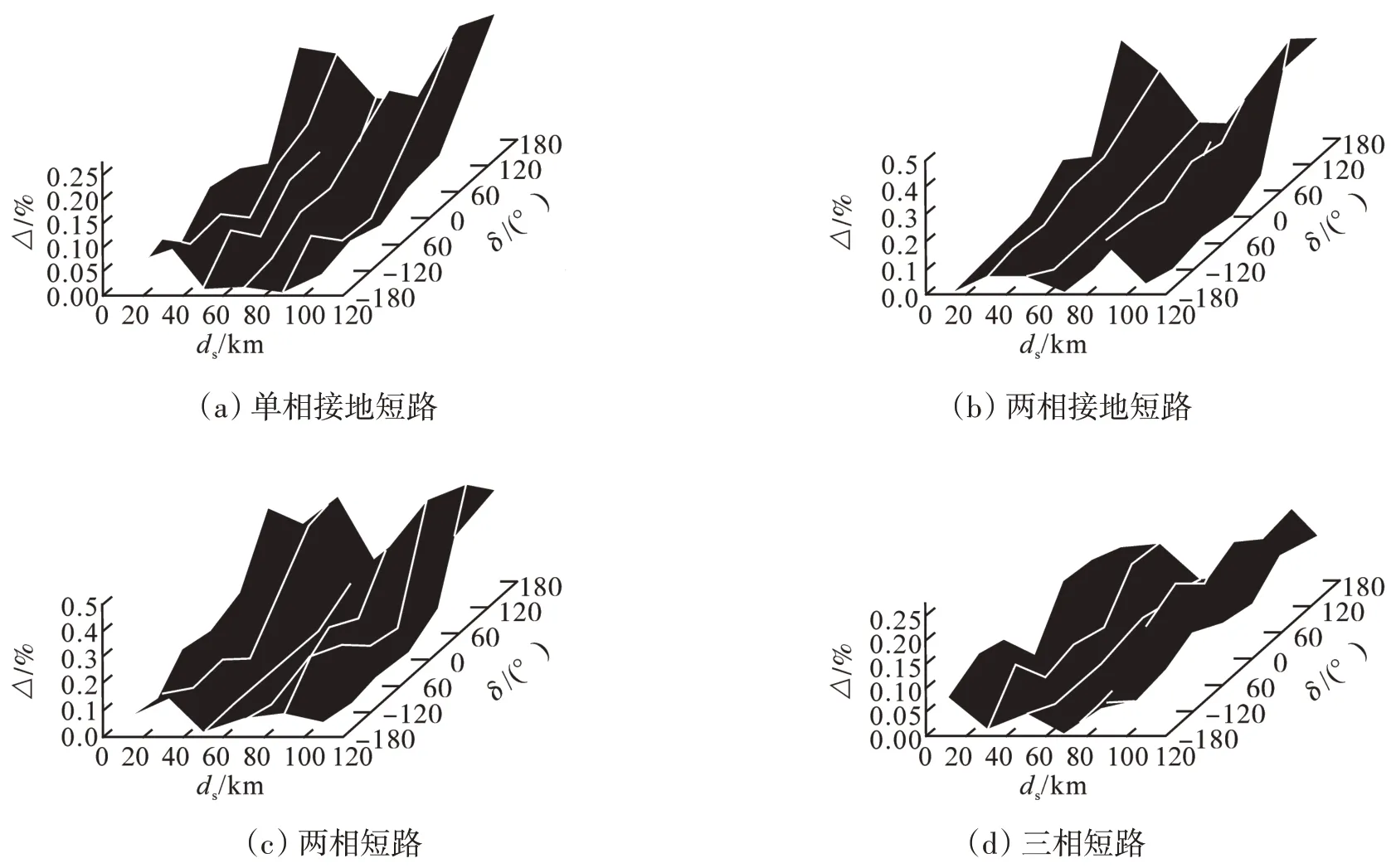
图3 各种短路故障的测距误差Fig.3 Fault location error of all short-current fault
4 结论
基于输电线路集中参数模型提出了双端测距新方法,适用于各种金属性短路故障。该方法主要利用故障阻抗计算和共轭法构造了故障距离一元二次方程,该方程的求解与伪根判别方便。仿真表明该方法简易可行,测距精度高,且不需要双端数据同步。但是,该方法还存在不足之处,不能适用于非金属性短路故障,具体方法有待进一步研究。
[1]葛耀中.新型继电保护和故障测距的原理与技术[M].西安:西安交通大学出版社,2007:256-257.
[2]何人望.电力贯通线故障测距方法的适应性分析[J].华东交通大学学报,2003,20(1):16-19.
[3]邱万英.一种电力贯通线单相接地故障测距的新方法[J].华东交通大学学报,2010,27(4):48-51.
[4]杨丰萍,王喜燕.AT供电牵引网故障测距仿真研究[J].华东交通大学学报,2012,29(5):34-37.
[5]MEKHAMER S F,ABDELAZIZ A Y,M EZZAT&T S.Abdel-salam.fault location in long transmission lines using synchronized phasor measurements from both ends[J].Electric Power Components and Systems,2012,40(7):759-776.
[6]徐鹏,王钢.双端非同步数据故障测距的非线性估计算法[J].继电器,2005,33(1):16-20.
[7]蒋春芳,王克英.基于参数估计的双端不同步故障测距算法[J].继电器,2008,36(1):1-4.
[8]李勋,石帅军,龚庆武.采用信赖域法和双端非同步数据的故障测距算法[J].高电压技术,2010,36(2):396-400.
[9]张爱枫.不需要双端数据同步的工频故障测距新方法[J].重庆大学学报,2003,26(8):78-81.
[10]施世鸿,何奔腾.基于分布参数模型的双端非同步故障测距算法[J].电网技术,2008,32(9):84-88.
[11]陈铮,董新洲,罗承沐.单端工频电气量故障测距算法的鲁棒性[J].清华大学学报,2003,43(3):310-313.
