计算机浮点运算的尾数处理

柴晓东

（黄河科技学院国际学院，河南郑州 450063）

一、计算机浮点运算

计算机中的浮点数是小数点的位置不固定，可以浮动的数据。浮点数的引入，不仅扩大了数据的表示范围，同时也提高数据的分辨精度。浮点数的表示方法类似于十进制科学标识法，就是用符号、一串有效数字（通常称作尾数）以及对应于比例因子中隐含基数的指数来表示一个数[1]。浮点数可表示为：N=2E·M。其中E是阶码，常用移码表示，它决定了浮点数的表示范围。M是尾数，是定点纯小数，它给出了有效数字的位数，决定了浮点数的分辨精度。

计算机中浮点数的加减运算步骤主要有：对阶、尾数运算、规格化处理、舍入处理以及溢出处理。对阶就是通过移动尾数，使要进行加减运算的两个浮点数的阶码相等。尾数运算就是将对阶后的浮点数尾数，按照运算规则，进行求和运算。规格化处理就是将运算结果通过一定的方法，变换成统一的标准格式。舍入处理就是根据运算要求，对运算结果中，多出保留位的数值进行丢弃或进位处理。溢出处理就是对运算结果中，可能产生的阶码溢出，或尾数溢出进行相应的处理。在以上运算步骤中，尾数的规格化处理、舍入处理以及溢出处理，都属于尾数处理部分。

二、规格化处理

浮点数进行运算后，若不对浮点数的表示做出明确规定，同一个浮点数的表示就不是惟一的[2]。为了充分利用尾数的位数来表示更多的有效数字，以提高数据的分辨精度，通常采用浮点数规格化形式。规格化就是将尾数的绝对值限定在某个范围内，使尾数部分的绝对值尽可能以最大值的形式出现。规格化浮点数的尾数应满足条件：0.5≤│M│＜1。

（一）原码、补码的规格化

浮点数规格化的表示形式与尾数采用何种编码有关。

当尾数用原码表示时，若0≤M，尾数规格化形式为：M＝0.1XX…XX。若0＞M，尾数规格化形式为：M＝1.1XX…XX。其中X为0或1，以下相同。即当尾数为正数时，其规格化形式要求，尾数小数点后第一位的值为1；当尾数为负数时，尾数小数点后第一位的值为1。

当尾数用补码表示时，若0≤M，尾数规格化形式为：M＝0.1XX…XX。若0＞M，尾数规格化形式为：M＝1.0XX…XX。即当尾数为正数时，其规格化形式要求，尾数小数点后第一位的值为1；当尾数为负数时，尾数小数点后第一位的值为0。

综上所述，浮点数的规格化，其实质就是为了保证尾数所对应的真值小数点后第一位的值为1。当浮点加减运算的结果不是规格化的形式时，需要进行左规或者右规将它转化为规格化形式。双符号数补码规格化形式为：M＝00.1XX…XX或M＝11.0XX…XX。规格化方法是：

1.若加减运算结果的两个符号位不同，如01.XXX…XX或10.XXX…XX，表明运算结果发生了溢出，此时需将尾数右移1位（小数点左移1位），阶码加1，即进行右规。例如，若加减运算结果是01.110111，阶码为10，规格化需要右规1位，阶码加1，规格化后的形式为00.1110111，阶码变为11；若加减运算结果是10.110111，阶码为10，规格化需要右规1位，阶码加1，规格化后的形式为11.0110111，阶码变为11。

2.若加减运算结果的两个符号位相同，但最高数值位与符号位相同，如00.0XX…XX或11.1XX…XX，此时需将尾数左移（小数点右移），直至转化为00.1XX…XX或11.0XX…XX的形式，阶码减去尾数左移的位数，即进行左规。例如，若加减运算结果是00.010111，阶码为11，则规格化需要左规1位，阶码减1，规格化后的形式为00.101110，阶码变为10；若加减运算结果是11.110111，阶码为11，则规格化需要左规2位，阶码减2，规格后的化形式为11.011100，阶码变为01。

（二）IEEE754标准浮点数的规格化

为了便于软件的移植，浮点数的表示形式应该有统一的标准。IEEE（Institute of Electrical and Electronics Engineers）提出了IEEE754标准。IEEE754标准规定基数为2，符号S用0或1表示，阶码E用移码表示，尾数M用原码表示。如图1所示为IEEE754标准32位浮点数和64位浮点数的格式。

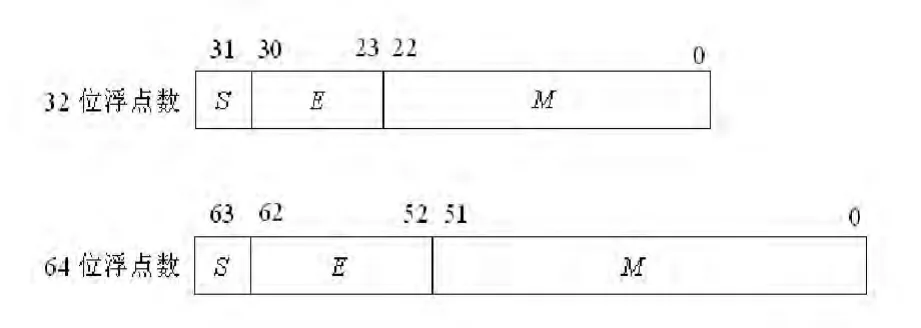
图1 IEEE754浮点数格式

对于IEEE754标准的浮点数，由于其尾数M用原码表示，因此，其规格化方法与原码规格化方法相同。根据原码的规格化方法，尾数小数点后第一位的值为1，规格化后，尾数M的最高位应该是1。对于32位浮点数，尾数M的范围是0～22位，规格化后，尾数M最高位应该为1，即第22位应该为1。对于64位浮点数，尾数M的范围是0～51位，规格化后，第51位应该是1。因浮点数规格化后，尾数M最高有效位固定为1，即尾数M最左位固定为1，IEEE754标准将这个1缺省存储，即不存储，而隐藏在二进制小数点的左边。这样M域中存储的23位和52位实际上只表示了尾数的小数部分，即小数点右方的各位。

图2所示为IEEE754标准32位浮点数的规格化。其中（a）图表示是一个非规格化数+0.0001101…×27的IEEE754标准格式，其中阶码用移码表示。阶码原始是9，变为移码后为7+127，二进制为10000110。尾数域的数据为0.0001101…。将尾数0.0001101…规格化，按照原码规格化方法，左规3位，规格化后变为0.1101…，阶码减3，变为4。由于IEEE754标准规定，尾数域最高位隐藏不存储，即小数点左边应该为1，则需要对规格化后的值再次进行变换，即小数点向右再次移动1位，变为1.101…，阶码再减1，变为3。阶码用移码表示为3+127，二进制表示形式为10000010。尾数域数据为101…。（b）图表示的即为规格化后的IEEE754标准格式。其中最高位0是符号位，表示“+”。

事实上，IEEE754标准浮点数规格化后，尾数域的数据只是小数点后的数据，实际上尾数表示范围比实际存储的多一位，这一位就是小数点前的一位1。

图2 IEEE754标准32位浮点数规格化

三、舍入处理

在浮点运算中，在执行右规或对阶时，尾数低位上的数值会因为超出机器的允许位数而被移掉，从而使数值的精度受到影响。为了减小数据的误差，需要对移掉的数据进行舍入处理。计算机中常用的舍入方法有两种：四舍五入法和截断处理法。

（一）四舍五入法

四舍五入法类似于十进制的四舍五入，即尾数超出规定的保留位的多余位数值，若大于规定的保留位的最低有效位值的一半时，则需要进位，即在尾数保留位的最低有效位上加1。若超出规定的保留位的多余位数的值，小于规定的保留位的最低有效位值的一半时，则直接舍去。例如，若要进行舍入处理的数据为0.11011001，要求保留位为4位。则进行舍入处理的多余数据为1001，由于1001大于1000，因此需要向高位进位。将0.1101的末位直接加1，即0.1101+0.0001=0.1110，舍入处理结果为0.1110；若要进行舍入处理的数据为0.11010001，要求保留位为4位。则进行舍入处理的多余数据为0001，由于0001小于1000，因此需要舍去。直接将0001舍去，保持其它数值不变，舍入处理结果为0.1101。

对于多余位刚好等于有效位值的一半时，分两种情况处理：当规定的保留位的最低有效位为0时，则直接舍去；若规定的保留位的最低有效位为1时，则向高位进一位使其变为0。例如，若要进行舍入处理的数据为0.11001000，要求保留位为4位。保留位的最低有效位为0，则直接舍去多余位1000。舍入处理结果为0.1100。若要进行舍入处理的数据为0.11011000，要求保留位为4位。保留位的最低有效位为1，则向保留位的最低位加1，即0.1101+0.0001=0.1110，舍入处理结果为0.1110。

四舍五入法的舍入结果最接近于被舍入处理的数据，而且是无偏近似。但该方法要求一次加法运算，有可能需要对舍入结果再次进行规格化。这种舍入方式是IEEE浮点标准舍入处理的默认模式。

（二）截断处理法

截断处理法是一种简单的方法，直接将超出规定的保留位的多余位舍去，而剩余的规定的保留位则保持不变。例如，若要进行舍入处理的数据为0.11011001，要求保留位为4位。则进行舍入处理的多余数据为1001，直接将多余位1001舍去即可。舍入处理结果为0.1101。截断处理方法操作简单，但误差相对较大，影响结果的精度。

四、溢出处理

在浮点运算过程中，需要检测计算结果是否发生溢出。如果溢出，需要进行溢出处理。溢出有两种，一种是阶码溢出，另一种是尾数溢出。

阶码的溢出有两种情况，一种是两个同符号数据相加，由于一个数据的绝对值很大，已经使正阶码达到最大值，两数相加规格化后，阶码需要增加，这时发生阶码上溢。另一种是两个不同符号数据相加，由于两个数据的绝对值很小，两数相加规格化后，阶码需要减少，这时发生阶码下溢[3]。

尾数的溢出也有两种情况，一种是两个同符号数据相加，出现相加结果最高位向上进位，需要将尾数右移，阶码加1。即对计算结果进行右规格化处理。另一种是两个数据运算后，数据长度超出了要求的数据长度，这时需要对计算结果进行舍入处理。由于浮点数的表示范围很广，在实际应用中，阶码的溢出很少出现，但尾数的溢出出现较多。

[1]Carl Hamacher等.计算机组成[M].北京：机械工业出版社，2004.

[2]白中英.计算机组成原理（第四版）[M].北京：科学出版社，2008.

[3]罗克露，刘辉等.计算机组成原理（第二版）[M].北京：电子工业出版社，2010.