深读与妙用：敞亮教材的价值空间

叶柱

教材对于教学的重要性，毋庸置疑。《数学课程标准》（2011年版）指出：“数学教材为学生的数学学习活动提供了学习主题、基本线索和知识结构，是实现课程目标、实施数学教学的重要资源。”那么，作为一名数学教师，我们该如何直面数学教材呢？笔者认为，“深读”是前提，“妙用”是重点。

一、深读：挖掘教材的价值内涵

备课时，面对一则教材文本，很多教师通常习惯于改情境、换材料、变例题、调习题，而很少意识到，大到整体结构，小到细节图文，教材文本无处不凝聚着编者的编写意图。所以，充分解读教材文本，准确领会编写意图，是实现“用教材教”课程理念的基本前提。在此，以《多位数乘一位数的笔算》（新人教版数学三年级上册）为例，谈谈教材解读的三个基本要点。

1.从高到低，读清课程理念

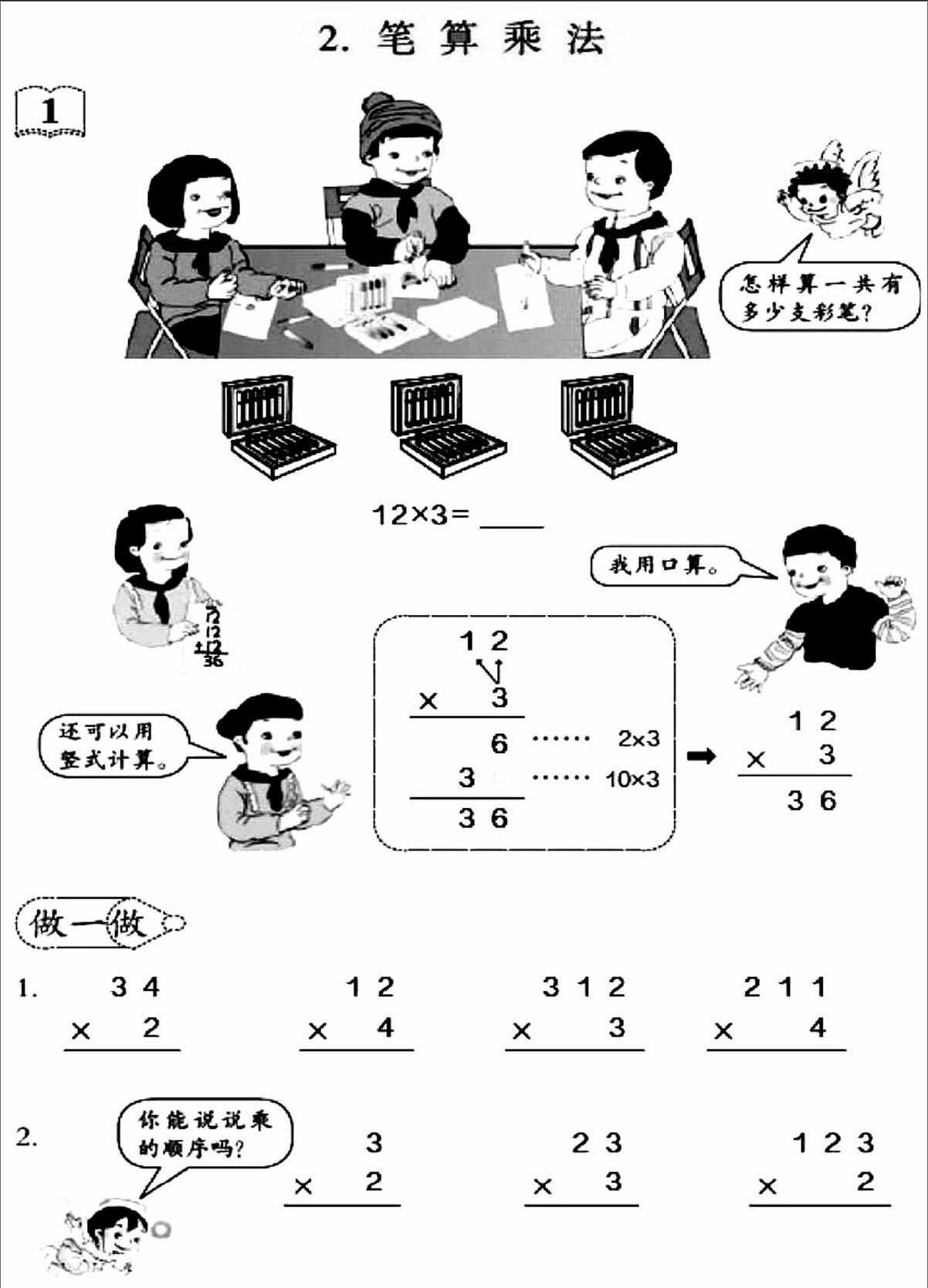
课程标准是教材编写的依据，我们应该依托课标精神，思辨教材内涵。要着重弄清楚的是，这则教材内容属于哪个课程领域？亟须落实的课程核心词是哪个？文本编排的体例特点暗合了哪条课程理念？我们来看，《多位数乘一位数的笔算》隶属于“数与代数”领域中“数的运算”板块，需要重点关注的课程核心词是“运算能力”。明确了这一点，教师才能带着“既应澄清算理，又要落实算法”的施教导向，来认识教材内容的核心价值，而不至于随意改换、盲目处理。另外，本课教材一开始呈现了“三位小朋友画图”的生活场景，从中引出“一盒水彩笔有12支，3盒一共多少支”的实际问题。教师切忌将此情境仅仅作为引出计算例题的幌子，而应敏感地觉察到，教材“算用结合”的编写体例，承载了“增强发现和提出问题的能力、分析和解决问题的能力”的“四能”目标。唯有如此，才能真正发挥教材情境在培养学生解决问题的能力方面的重要作用。

2.由远及近，读顺知识结构

任何一个知识点都非孤立存在，而是各有其“前世今生”。因此，研读教材时，要重视挖掘知识之间的逻辑联系，使得教学活动能够彼此呼应、整合推进。这里所说的由远及近，包含了两层意思。其一，纵向观照，了解知识体系。《多位数乘一位数的笔算》一课的教学内容，是在学生掌握“表内乘法”“整十整百数乘一位数口算”“乘加两步混合运算”及“万以内数的组成”的基础上进行编排的，并为今后继续学习笔算乘法作好铺垫。明确了这一来龙去脉，教师看待教材文本才不会断章取义。其二，横向扫视，把握单元走向。关于笔算乘法，整个单元共编6个例题。例1（本课内容）是“不进位乘法”，例2、例3是“进位乘法”，例4是“0的乘法”，例5、例6分别是“因数中间、末尾有0的乘法”。从中我们不难发现，本课教学意义重大，是学生全面学习笔算乘法的开端。因此，解决“笔算乘法从哪位乘起、该如何书写”等基础性规范问题，是本课教学的重点。

3.自粗而细，读透文本材料

较为充分的背景研读之后，我们需要将目光聚焦到教材文本的具体细节，剖析其中的编写意图，并尽可能基于学生视角，对学习材料的可行性作出客观评析。首先，解读情境。教材设计了“3盒水彩笔一共多少支”的问题情境，符合儿童的生活现实；同时，“每盒12支”可以根据需要拆分成“10支+2支”，有利于算理分析。其次，解读例题。呈现“12×3=”后，教材通过几位小朋友的对话，展示了本课需要关注的三种算法，分别是“竖式连加”“口算乘法”“竖式乘法”。解读这部分内容时，要根据学生的认知基础，客观分析每种算法的知识源头及课堂生成的可能性。显然，“竖式连加”基于乘法与加法的联系，学生可能自主生成；“口算乘法”指向上节课的已学知识，学生也会及时想到；而“竖式乘法”属于首次接触，也是本课新授内容，学生较难探究得出，但可通过“口算乘法”加以迁移。有此分析后，教学引导便能胸有成竹：无须强求“竖式乘法”的及早出现，重在挖掘算法之间的内在联系、支撑乘法竖式的模型建构。最后，解读习题。“做一做”中有一组题目：3×2，23×2，123×2。我们需要思考，编写目的是什么？显然，通过组织学生依次计算、有序观察，助其强化“笔算乘法由个位开始”的策略思想，是本组习题的话外之音。教师如果没能领会这一意图，视其为三道独立的笔算题，那么，就难以发挥习题内在的结构化功能了。

概而言之，解读教材文本时，每位教师都应树立“从高到低”“由远及近”“自粗而细”的“镜头拉伸”意识，读清理念，读顺结构，读透材料，为完善教学资源、优化教学设计、改进教学行为打好基础。

二、妙用：扩张教材的价值功能

当前，数学教师在使用教材时至少存在三种误区：其一，“零处理”，照本宣科。“教教材”成了课堂教学的唯一任务，上课过程等同于“演课本剧”。其二，“全处理”，另起炉灶。有些教师盲目丢弃课本资源，一味引入生活元素，造成了“花样素材一贯到底、教材资源不见踪影”的课堂怪状。其三，“乱处理”，盲目裁接。由于缺乏对教材内容的深层解读，教师难以把握教材内容的整体线索及核心要义，随意裁剪，胡乱嫁接，教学资源的结构优化难以实现。

反思上述误区，不难发现，创造性使用教材显得尤为重要。笔者认为，创造性使用教材的价值取向，在于依托教材的丰富内涵、构建有效的课堂资源，使之能更好地贴近学生现实、激活主体思考、促进意义建构。具体地说，需关注以下四个方面。

1.创造性使用教材，需要挖掘内涵

材料能呈现一种事实，反映一种线索，提供一种表象，但无法更深地揭示原理。这就是说，教师首先要对本课教学的数学本质做到了然于胸、心中有数，在此基础上，对简单浅显的课本材料加以细节聚焦、深层挖掘，帮助学生透视材料表面、充分领会背后蕴含的数学原理。

例如，《长方形、正方形面积的计算》（原人教版数学三年级下册），教材在揭示面积计算公式后，编排了一道例题（如下面左图）。学生独立解答完后，笔者追问：“咦，前面的学习中，我们计算的面积都以平方厘米作单位，为什么这道题用平方分米作单位呢？”刚开始，学生确实没有意会，都认为“因为题中写着平方分米，所以就用平方分米”。后来，随着老师的启发引导，学生慢慢有了感觉：之所以用平方分米作单位，是因为用来测量餐桌面积的工具，不再是“1平方厘米的正方形”，而是“1平方分米的正方形”，所以，测得的面积用平方分米作单位。在此基础上，笔者继续组织对话、促进体会：“长14分米”说明一行能摆14个1平方分米的面积单位，“宽9分米”说明能摆9行。所以，一共能摆126个1平方分米的面积单位。由此，通过对例题背景的跟进探究，帮助学生重温了面积计算公式推导过程的思维图式（如下面右图）。endprint

2.创造性使用教材，需要讲究方式

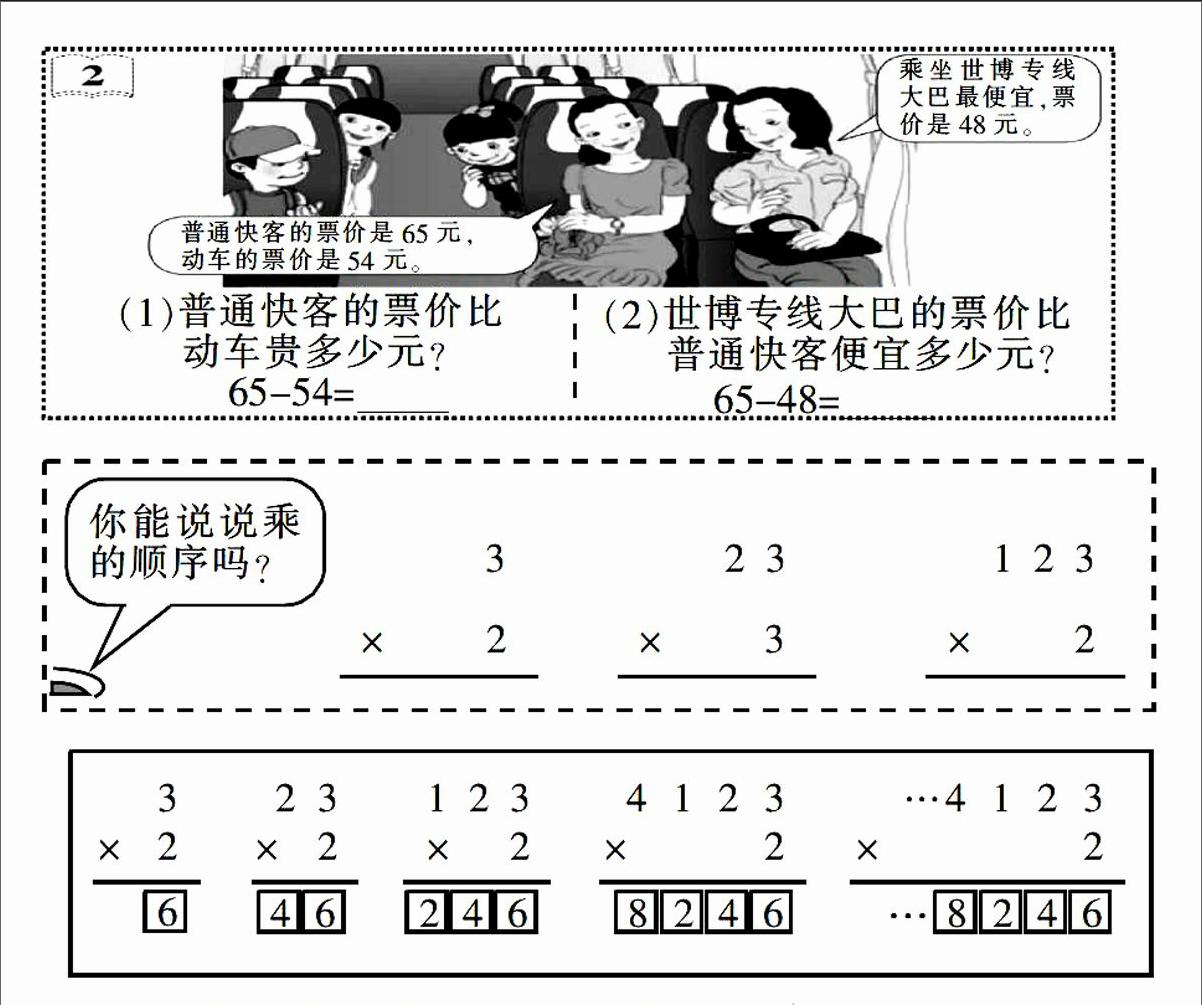
教材编排有相对固定的逻辑顺序。落实到课堂教学中，这种逻辑顺序还得根据需要灵动微调。比如计算内容的教材编排，大多由解决问题引出例题，随后呈现算法、提示算理。但是，假如每节课均按此思路教学，学生必定因为雷同而感觉乏味，而且也容易让教学活动进入“形式化”误区。笔者认为，适当改变教材内容的呈现方式，既能推动目标达成，又可体现教学新意。例如，《两位数减两位数口算》（新人教版数学三年级上册），教材中例2主要通过“乘坐交通工具”的问题情境引出“65-54”（不退位）、“65-48”（退位）两道例题。有位教师组织教学时，引入部分舍去情境，在一组口算训练中引出（1）“65-54”并展开教学。完成后，教师出示教材主题图（如下图，隐掉问题和算式），问学生：“我们刚才研究的65-54，能解决这幅图中的什么数学问题呢？根据图中的信息，你还能解决其他的数学问题吗？”随后顺势引出“大巴比快客便宜多少元”的问题，教学（2）“65-48”。这样组织，使教材主题图成为算用结合的中介、内容递进的桥梁，学生发现问题、提出问题、分析问题及解决问题的能力在此得以切实，得到历练。

普通快客便宜多少元？][65-48= ][乘坐世博专线大巴最便宜，票价是48元。]

3.创造性使用教材，需要重组内容

前段时间，笔者观摩了一节《四则运算》（原人教版数学四年级下册）的教学。全课下来，教师先后组织学生参与了四道例题的学习。

（1）3位叔叔去“冰雪天地”玩。成人票每张24元。他们带了100元，买票后还剩几元？

（2）儿童票半价。一张成人票和一张儿童票共多少元？

（3）每双滑雪鞋租金100元，每副手套租金10元。租3双滑雪鞋和1副手套共多少元？

（4）星期天，爸爸妈妈带着玲玲去“冰雪天地”游玩，购门票需要花多少钱？

四道例题分别指向“乘减”“除加”“乘加”“乘除加”四种类型，能帮助学生有序掌握混合运算的顺序。可是，翻看教材内容，笔者发现该课只安排了一道例题（如下图），即“乘除加”。那么，执教者为什么要把一道例题“扩容”为四道例题呢？这位老师道出了缘由：教材例题的运算类型是“乘除加”。通过此例，学生既要掌握“先乘除，后加减”的基本要领，还要体会“加法两边的乘除可以同时运算”的变式规则，显得“难点集中”。而改变成四道例题后，既呼应了教材情境，又拉伸了体验空间，使学生能先重点聚焦基本要领，再跟进关注变式规则，学习由此显得有序。确实，现行教材限于篇幅，所编材料常常高度概括、较为浓缩。对此，教师有必要遵循“从易到难，逐步深入”的教学原则，立足课本材料，进行合理重组，使之更符合学生的认知规律。

4.创造性使用教材，需要刷新取向

我们不能回避，有些内容教材在编排上似乎存在功利性的“近视”弊端。就是说，为了突出本课的核心知识，教材设定了一些呈现方式。而恰恰是这种呈现方式，从某种意义上看，是与学生数学素养的整体养成背道而驰的。此时，教师需要适当刷新教材内容的价值取向，确保教学过程更有利于学生的全面发展。

例如，《简便计算》原人教版数学四年级下册的主要内容是运用“减法的运算性质”简便计算。教材（如右上图）从解决问题的情境引入，突出了算用结合。然而，稍加分析，笔者有了困惑：面对“还剩多少页没看”的问题，学生会像“商量好似的”整齐划一地用“234-66-34”来列式吗？教材将列式统一为“234-66-34”，确实有利于突出运算规律的探究重点，但却在关注落实课时目标的同时，忽略了让学生充分经历解决问题的自主过程。因此，使用本课教材时，教师应适度放大对解决问题的聚焦程度，放手让学生列式解答，并在寻求“234-66-34”与“236-（66+34）”两种解法的逻辑关联的过程中，得出“减法的运算性质”。

得出笔算答案而设的，估算是为笔算服务的。而事实上，估算与笔算、口算一道，是“用运算解决问题”的三种常用方法。而且，课标将“寻求合理简洁的运算途径解决问题”作为衡量“运算能力”的重要指标，因此，虽然本课教学重点是笔算，教师也不必急于列式（因为“92÷30=”的算式形态本身就暗示着精算而非估算），而应该让学生“选

择自己喜欢的方式解决问题”。在没有束缚的情况下，有学生用口算解决了问题，有学生用估算解决了问题，还有学生用笔算解决了问题。对此，教师便可精要点拨“解决问题时，我们需要选择合适的运算方法”，并在此基础上将关注重点引向笔算。这样一来，计算教学的立意显得更具内涵了。endprint