双刀并行数控车削中的切削参数优化方法

谢书童 郭隐彪

1.集美大学，厦门，361021 2.厦门大学，厦门，361005

0 引言

制造领域中，数控加工切削参数的选择直接关系到加工成本、加工效率，以及加工质量。因此，在一定加工约束条件下，选择合理的切削参数可以实现特定的加工目标，例如降低加工成本、提高加工效率等，这就是切削参数优化问题［1－3］。

早期的切削参数优化研究主要集中在单刀车削加工，即多把刀具轮流车削，但每一时刻只有一把刀具在车削。常见的切削参数寻优算法有模拟退火 算 法［4］、遗 传 算 法［5－7］、蚁 群 算 法［8－10］、粒子群 算 法［11］、差 分 进 化 算 法［12］、分 布 估 计 算法［13－14］等。

近些年，人们开始把切削参数优化的研究重心从单刀车削逐渐转向双刀并行车削。双刀并行车削中的切削参数优化是多刀具同时优化问题，它的数学模型更复杂，求解难度更大，目前相关的研究工作还很少。Tang等［15］以最小化加工时间为目标，用粒子群算法对双刀车削中的多种加工方式进行优化。Xie等［16］在双刀并行车削中以最小化加工成本为优化目标，用分布估计算法优化加工参数。这些方法能得到一些优化解，但难以保证寻到全局最优解，且运算效率较低，不利于集成到车床的CAPP系统中。

针对对称式双刀并行车削中的切削参数优化问题，本文建立以最小化加工成本为目标的双刀并行车削参数优化模型。针对该模型提出一种混合优化算法，通过把蚁群算法（ant colony optimization，ACO）和子问题枚举算法（enumeration algorithm of sub－problems，EAS）相结合的方式，使得最终的优化算法具有寻优能力强、运算效率高的优点。

1 双刀并行车削参数优化模型

对称式双刀并行车削加工方式如图1所示。文献［4］建立的单刀车削参数优化模型接近实际车削加工，因此本文以它为基础，建立双刀车削参数优化模型。待优化的车削参数包括粗车、精车两个阶段的切削速度、进给量、切削深度、粗车次数，将工件加工成本作为优化目标，它由以下4个部分组成。

图1 双刀并行车削加工示意图

（1）实际切削过程中的加工成本CM。双刀车削的实际车削时间比单刀的车削时间［4］减少约一半，所以粗车时间为

精车时间为

式中，tmr、tms分别为粗车时间和精车时间，min；n为粗车次数，n＝ （dt－ds）／dr；L、D 分别为工件的长度和直径，mm；vr、vs分别为粗车和精车的切削速度，m／min；fr、fs分别为粗车和精车的进给量，mm／r；dt、dr、ds分别为车削总余量、粗车和精车的切削量，mm。

因此切削加工成本为

式中，k0为单位时间的管理成本和工人成本之和，＄／min。

（2）刀具空走和工件装卸操作所用成本CI。刀具空走和工件装卸操作成本与单刀车削的情况一致［4］：

式中，h1、h2分别为与车刀空走时间和进刀／退刀时间有关的常量；tc为换刀时间，min。

（3）换刀操作成本CR。双刀并行车削加工共有4把刀，粗车刀和精车刀各2把，2把粗（精）车刀同时进行车削加工。刀具寿命由Taylor公式确定，粗车刀的寿命为

精车刀的寿命为

式中，Tr、Ts分别为粗车刀和精 车刀的寿命，min；C01、C02、p、q、r均为 Taylor公式的系数［4］。

2把刀同时车削，换刀的时间为换2把刀的时间之和，粗车刀的换刀时间为2tetmr／Tr，精车刀的换刀时间为2tetms／Ts。其中，te为工件装卸的时间，min。因此总的换刀时间为

所以换刀操作成本为

（4）刀具磨损成本CT。刀具在粗车、精车过程中的加工条件不同，粗精刀具的磨损程度也不同，因此2把粗车刀的磨损成本为2krtmr／Tr，2把精车刀的磨损成本为2kstms／Ts。其中，kr、ks分别为粗车、精车刀刃成本，＄／刀刃。所以刀具磨损成本为

因此最终车削加工的加工成本函数为

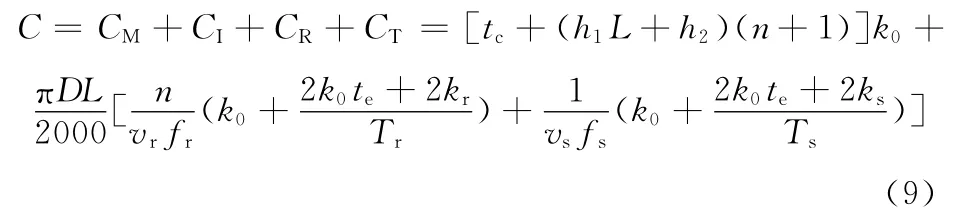
详细加工约束条件见文献［4，12］。本文目标是在满足车削加工约束条件下，最小化加工成本。

2 加工成本理论下限的计算方法

对称式双刀并行车削加工是由多次等进刀量的粗车和一次精车组成。不同的粗车次数将产生不同的加工情况。因此，各种可行加工情况的总数为

式中，nU、nL分别为粗车次数的上下限［14］。

求解整个车削参数优化问题就等效于求解m个较小的子问题。为了避免穷举m个子问题，同时也为了评价实验结果，先计算出每个子问题的加工成本的理论下限。例如，对于粗车次数为n0车削子问题，其加工成本理论下限的计算过程如下所述。

根据式（9）可得

那么

式中，（vrfr）U、（vsfs）U分别为vrfr、vsfs的上限值。因此，粗车次数为n0的车削子问题的加工成本的理论下限为

由于式（13）中的参数均已知，故只需通过约束条件的缩放处理计算出（vrfr）U和（vsfs）U，就可算出理论下限。通过上述计算方法，可计算出不同车削子问题的加工成本理论下限，最小的加工成本理论下限就是整个优化问题的理论下限。

3 算法

针对复杂的车削参数优化问题，先采用子问题枚举算法对问题进行分解、排序、预处理，再运用蚁群算法对子问题进行全局寻优求解。由此提出的基于蚁群算法和子问题枚举算法的混合优化算法能更有效地解决切削参数优化问题。

3.1 子问题枚举算法

为了降低问题的复杂度，提高算法的效率，采用子问题枚举算法对问题进行分解、排序、预处理，算法的主要步骤如下：

（1）根据可能的加工情况数，把整个优化问题等效分解成m个子问题。

（2）使用第2节的加工成本理论下限的计算方法，计算出每个子问题的加工成本理论下限CnL。

（3）按子问题的加工成本的理论下限CnL大小的升序排列所有子问题，依次为第1子问题，第2子问题，…，第m子问题，其相应的粗车次数分别为N1，N2，…，Nm，理论下限分别为第一理论下限C1L，第二理论下限C2L，…，第m理论下限CmL，其中，C1L≤C2L≤ … ≤CmL。

（4）设定i＝0。

（5）i←i＋1。

（6）利用蚁群算法在第i个子问题的解空间中寻得优化解CiO。

（7）若优化解min（C1O，C2O，…，CiO）≤C（i＋1）L或i＝m，转步骤（8）；否则转步骤（5）。

（8）从已经得到的优化中选出最小解作为最优解，算法终止。

子问题枚举算法通过优先求解少数子问题来解决整个车削参数优化问题，从而大大缩短了算法的枚举时间［14］。举例说明，某一车削优化问题被分解成8个子问题，每个子问题的加工成本理论下限均被计算出来。子问题的加工成本理论下限升序排列后为2.51＄、2.65＄、2.72＄、2.88＄、3.10＄、3.17＄、3.31＄、3.48＄。步骤（6）的蚁群算法在第1子问题（理论下限为2.51＄的子问题）处找到优化解C1O（为2.68＄），由于C1O＞C2L（C2L为2.65＄），不满足步骤（7）的条件，蚁群算法就转到第2子问题处搜索优化解，寻得优化解为2.71＄，这时 min（2.68＄，2.71＄）＜2.72＄，即 min（C1O，C2O）＜C3L，所 以 min（2.68＄，2.71＄）为整个优化问题的最优解，算法终止。其主要原因是：在后续子问题中找到的优化解必大于或等于其相应的理论下限，则必大于或等于C3L（为2.72＄），所以剩下的5个子问题均不必搜索，换句话说，子问题枚举算法只需处理8个子问题中的2个就可解决整个复杂车削优化问题。

3.2 基于蚁群算法与子问题枚举算法的混合优化算法

蚁群算法（ACO）和子问题枚举算法（EAS）相结合的优化算法（ACO－EAS）的主要步聚如下：

（1）令i＝0。

（2）令i←i＋1；以第i个车削子问题为出发点，开始搜索。

（3）初始化种群，在第i个车削子问题中进行个体编码与解码（目标函数计算）；设定迭代数l＝1。

（4）蚂蚁数nant＝1。

（5）按轮盘概率法为当前蚂蚁选择下一个城市（路径）。

（6）用局部更新规则更新信息素，蚂蚁数nant←nant＋1。

（7）判断蚂蚁数nant是否达到蚂蚁总数，若没达到，转步骤（4）。

（8）用全局更新规则更新信息素，迭代数l←l＋1。

（9）判断算法是否达到最大迭代数Gmax，若未达到，则转步骤（3）。

（10）输出当前子问题的优化解UiO；若优化解 min（U1O，U2O，…，UiO）≤U（i＋1）L或i＝m，转步骤（11）；否则转步骤（2）。

（11）从已经得到的优化解中选出最小解作为最优解，算法终止。

3.3 解的编码和解码

算法采用十进制数串的编码方式来表示问题的解［17-18］。具体的做法为：对于待优化子问题的5个变量vr、fr、vs、fs、ds，用定义域设为［0，1］的5个变量x1、x2、x3、x4、x5与之建立一一对应的函数关系。这样只需优化变量x1、x2、x3、x4、x5就可得到优化的相应加工参数vr、fr、vs、fs、ds。例如，对变量xi进行编码（要求精确到小数点后d位），则编码后的变量xi可用d个十进制数近似表示，于是构造10d＋2个“城市”。这些“城市”分为d＋2层，首尾两层各有1个“城市”（起始“城市”、终止“城市”），均为0（作为分隔层）。中间d层，从左往右分别表示变量的十分位、百分位等［18］。因此，5个变量就组成5d＋6层“城市”，两变量之间用0作为辅助层隔开。解用56位十进制表示，编码方式如表1所示。解码时，对各变量对应的层分别解码。

表1 解的编码

在解码处理中，通过一定的数学变换就可以把变量从定义域［0，1］变到原来的定义域。例如50≤vr≤500，那么对于0≤xi≤1，则由公式vr＝450xi＋50可得vr与xi的函数对应关系。其余变量fr、vs、fs、ds也做类似处理。

3.4 信息素更新规则和约束条件处理

蚁群算法中信息素的局部更新规则和全局更新规则采用文献［18］的更新方式。

针对模型中的加工约束条件，在算法中使用罚函数对违反加工约束条件的个体进行惩罚，以提高不满足约束的个体的目标函数值。违反不同的加工约束条件，将施以不同程度的惩罚。

4 模拟实验

算法用C＋＋实现，具体参数设定：蚁群大小为40，迭代总数为50，局部信息素更新系数ρ为0.2，全局信息素更新系数α为0.2，信息素初始化系数τ0为0.01。测试算法性能的加工实例的基本参数见文献［4，12］。

算法在 Windows平台（CPU为P4 2.0GHz、内存为1GB）上运行20次，运算时间为算法运行20次的时间总和。从表2可知，对于车削总余量不同的4个加工实例，算法运行稳定，所得结果的标准偏差小，算法运算效率高，约12s就可得到优化结果。此外，随着车削总余量的增加，相应的车削工序数也增加，但算法的运算时间没有明显增大。也就是，随着优化问题复杂度的增加，算法的时间花销没有明显增大。这有利于算法集成到数控车床的CAPP系统中。通过与分布估计算法［16］的结果对比发现，在不同加工实例中，本文算法优化后的加工成本平均值都明显小于分布估计算法，同时运算效率提高了8倍。

表2 不同算法的结果对比

最后，将2个算法所得的最优解与加工成本的理论下限进行对比，如图2所示。本文算法在不同加工例子中所得最优解均小于分布估计算法，非常接近理论下限，仅差4.9%，进一步优化的空间已经很小。优化的切削参数见表3。以上实验结果表明，ACO－EAS算法能找到优化的切削参数集，有效地降低加工成本。

图2 算法最优解与加工成本理论下限的对比（算法1为本文算法；算法2为分布估计算法）

表3 优化的切削参数

5 结语

为研究双刀并行车削加工中的切削参数优化问题，建立了双刀并行车削的参数优化模型，把蚁群算法与子问题枚举算法相结合，提出了ACOEAS混合优化算法。模拟实验结果表明：ACOEAS算法具有较强的搜索能力、较高的运算效率，能快速找到优化的车削参数，以降低加工成本。此外，提出了双刀并行车削的加工成本理论下限的计算方法，通过该方法算出的理论下限有助于提高算法的性能。

［1］Chandrasekaran M，Muralidhar M，Krishna C M，et al.Application of Soft Computing Techniques in Machining Performance Prediction and Optimization：a Literature Review［J］.International Journal of Advanced Manufacturing Technology，2010，46（5／8）：445－464.

［2］高亮，杨扬，李新宇.数控加工参数优化的研究现状与进展［J］.航空制造技术，2010（22）：48－51.Gao Liang，Yang Yang，Li Xinyun.Research and Development of Optimization of NC Machining Parameters［J］.Aeronautical Manufacturing Technology，2010（22）：48－51.

［3］Yusup N，Zain A M，Hashim S Z M.Evolutionary Techniques in Optimizing Machining Parameters：Review and Recent Applications（2007－2011）［J］.Expert Systems with Applications，2012，39（10）：9909－9927.

［4］Chen M C，Tsai D M.A Simulated Annealing Approach for Optimization of Multi－pass Turning Operations［J］.International Journal of Production Research，1996，34（10）：2803－2825.

［5］Onwubolu G C，Kumalo T.Optimization of Multipass Turning Operations with Genetic Algorithms［J］.International Journal of Production Research，2001，39（16）：3727－3745.

［6］Chen M C，Chen K Y.Optimization of Multipass Turning Operations with Genetic Algorithms：a Note［J］.International Journal of Production Research，2003，41（14）：3385－3388.

［7］Sankar R S，Asokan P，Saravanan R，et al.Selection of Machining Parameters for Constrained Machining Problem Using Evolutionary Computation［J］.International Journal of Advanced Manufacturing Technology，2007，32（9／10）：892－901.

［8］Wang Y C.A Note on Optimization of Multi－pass Turning Operations Using Ant Colony System［J］.International Journal of Machine Tools ＆ Manufacture，2007，47（12／13）：2057－2059.

［9］Xie S，Guo Y.Optimisation of Machining Parameters in Multi－pass Turnings Using Ant Colony Optimisations［J］.International Journal of Machining and Machinability of Materials，2012，11（2）：204－220.

［10］Vijayakumar K，Prabhaharan G，Asokan P，et al.Optimization of Multi－pass Turning Operations U－sing Ant Colony System［J］.International Journal of Machine Tools ＆ Manufacture，2003，43（15）：1633－1639.

［11］Raja S B，Baskar N.Optimization Techniques for Machining Operations：a Retrospective Research Based on Various Mathematical Models［J］.International Journal of Advanced Manufacturing Technology，2010，48（9／12）：1075－1090.

［12］Yildiz A R.Hybrid Taguchi－differential Evolution Algorithm for Optimization of Multi－pass Turning Operations［J］.Applied Soft Computing，2013，13（3）：1433－1439.

［13］谢书童，郭隐彪.边缘分布估计算法在车削参数优化中的应用［J］.中国机械工程，2010，21（1）：22－26.Xie Shutong，Guo Yinbao.Application of Marginal Estimation of Distribution Algorithms in Optimization of Turning Parameters［J］.China Mechanical Engineering，2010，21（1）：22－26.

［14］谢书童，郭隐彪.数控车削中成本最低的切削参数优化方法［J］.计算机集成制造系统，2011，17（10）：2144－2149.Xie Shutong，Guo Yinbao.Optimization Approach of Cutting Parameters for Minimizing Production Cost in CNC Turnings［J］.Computer Integrated Manufacturing Systems，2011，17（10）：2144－2149 .

［15］Tang L，Landers R G，Balakrishnan S N.Parallel Turning Process Parameter Optimization Based on a Novel Heuristic Approach［J］.Journal of Manufacturing Science and Engineering，2008，130（3）：031002－1－12.

［16］Xie S T，Pan L F.Optimization of Machining Parameters for Parallel Turnings Using Estimation of Distribution Algorithms［C］／／Proceeding of the 3rd International Conference on Advanced Engineering Materials and Technology.Zhangjiajie，2013：1192－1195.

［17］Dorigo M，Gambardella L M.Ant Colony System：A Cooperative Learning Approach to the Traveling Salesman Problem［J］.IEEE Transactions on Evolutionary Computation，1997，1（1）：53－66.

［18］陈烨.用于连续函数优化的蚁群算法［J］.四川大学学报（工程科学版），2004，36（6）：117－120.Chen Ye.Ant Colony System for Continuous Function Optimization［J］.Journal of Sichuan University（Engineering Science Edition），2004，36（6）：117－120.