基于混合算法的磁悬浮隔振器模型辨识与验证
2014-12-05宋春生张锦光张建国
宋春生 张锦光 张建国
1.武汉理工大学,武汉,430070 2.连云港鹰游纺机有限责任公司,连云港,222000
0 引言
隔振技术能有效抑制结构振动的能量传递,是潜艇减振降噪的关键技术。隔振分为主动隔振和被动隔振两种形式。被动隔振由其自身所限,对低频干扰隔振能力差,甚至对系统谐振频率附近的干扰信号还有放大作用。主动隔振可以根据设定的控制规律动态调整系统的支承特性参数,满足被动隔振无法实现的低频及谐振频率附近频率的隔振降噪的需要。
主动隔振已成为当今研究的热点,文献[1]表明,主动隔振的研究集中于主动隔振结构设计、主动隔振控制等领域。各种类的主动隔振器如电流变液阻尼器[2]、磁流变液阻尼器[3]、电磁隔振器[4]、压电隔振器等是近几年研究的热点。与其他主动隔振技术相比,磁悬浮隔振技术具有频响范围宽、响应快、可靠性高和控制参数易于调控的优势。应用磁悬浮隔振器能够有效解决多源复杂激励隔振系统隔振性能不足的问题,磁悬浮隔振器已被广泛应用于主动隔振系统,并取得了较好的隔振效果[5]。但磁悬浮隔振器的非线性、磁滞等会影响到主动隔振效果,磁悬浮隔振器工作频率较高时,这种滞后对隔振效果影响更大,解决这一问题的根本途径就是得到精确描述磁悬浮隔振器力、电流、位移之间关系的模型。目前,国内外学者主要运用电磁场理论的解析方法和利用实验数据的模型辨识方法建立此关系模型[6-7]。由于磁饱和、磁耦合及磁泄漏等因素,磁悬浮隔振器具有较强的非线性及磁滞,很难通过解析方法描述和求解,因此,利用解析方法很难精确描述磁悬浮隔振器动态电磁力、电流、位移之间的关系。基于实验实测数据的模型辨识方法是非线性及不确定模型建模的常用方法。对于存在时滞的系统,一般的模型辨识方法如最小二乘法等,不能得到较好的辨识结果。人工神经网络具有高度的非线性,能够进行复杂的逻辑计算和非线性关系实现,广泛应用于模式识别、控制与优化、预测与管理等领域。因此,本文提出一种基于混合训练算法的人工神经网络模型辨识方法,以得到精确描述磁悬浮隔振器动态电磁力、电流、位移之间关系的模型。
1 磁悬浮隔振实验平台系统
1.1 磁悬浮隔振系统模型
根据动力设备的隔振要求,本文建立的磁悬浮隔振实验台如图1所示,隔振实验台由激振电机、隔振基座、磁悬浮隔振器(具体结构见图2)、弹簧、导向装置及底座构成。磁悬浮隔振器与普通弹簧并联安装在隔振基座与底座之间。激振电机与隔振基座刚性连接,共同构成隔振对象。由于导向装置的作用,实验台只能沿竖直方向运动。
隔振实验平台中的力传感器用来测量弹簧力及磁悬浮隔振器的电磁力,位移传感器用来测量隔振基座的绝对位移。磁悬浮隔振器的性能对隔振效果起到至关重要的作用,因此研究磁悬浮隔振器特性是主动隔振的首要任务。

图1 磁悬浮隔振实验台
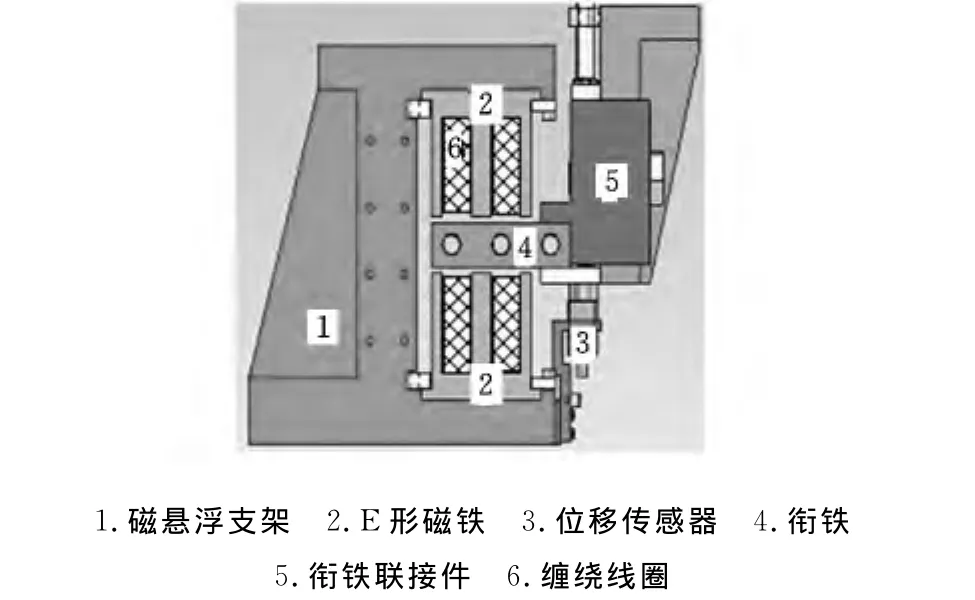
图2 磁悬浮隔振器机械结构图
1.2 磁悬浮隔振器模型
磁悬浮隔振器结构如图2所示,磁悬浮支架固定在基础上,衔铁及其组件固定隔振对象上,位移传感器测量衔铁和E形磁铁之间的气隙。
电磁力是决定磁悬浮隔振器性能的最重要特性。由于磁饱和、磁耦合及磁滞的存在,实际磁悬浮隔振器的电磁力很难通过理论模型精确描述,高频动态情况下,系统的时滞和非线性越发显著,动态电磁力模型更难通过相关理论建立。图3所示为15Hz下,实测的磁悬浮隔振器动态电磁力曲线,可以看出,由于磁滞的影响,在同一气隙、电流下,气隙变化方向也会影响电磁力的大小。基于实验实测数据的模型辨识方法是非线性及不确定模型建模的常用方法。对于存在时滞的系统,一般的模型辨识方法如最小二乘法等,不能得到较好的辨识结果。人工神经网络能够进行复杂的逻辑计算和非线性关系实现,因此,为了建立精确描述磁悬浮隔振器动态电磁力、电流、位移之间关系的模型,本文提出一种BP人工神经网络模型辨识方法。
2 BP神经网络辨识模型
BP神经网络被广泛应用于非线性系统的模式识别、控制与优化等领域,因此,本文根据动态电磁力的特性建立相应的BP神经网络,并采用不同的训练方法对所建立的神经网络进行训练,得到动态电磁力辨识模型。
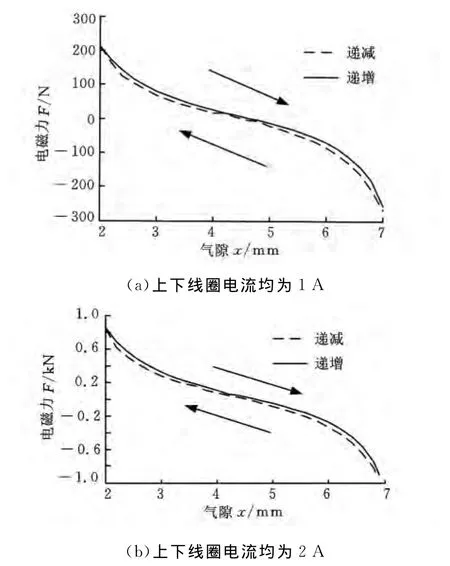
图3 实测磁悬浮隔振器动态电磁力曲线(15Hz)
经过反复分析和实验,建立的磁悬浮隔振器动态电磁力模型识别神经网络的结构为3-5-1,包括3个输入节点、5个隐含节点和1个输出节点。输入节点变量为气隙、气隙变化率、电磁力,输出节点变量为电流,隐含节点采用sigmoid型传递函数,输出节点采用线性传递函数。sigmoid型传递函数的表达式为
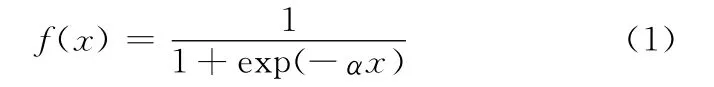
BP神经网络的结构如图4所示,x1、x2、x3为输入节点,对应气隙、气隙变化率、电磁力,wij为输入节点xj到隐含节点i的权值,Wi为隐含节点i到输出节点的权值,其中,i=1,2,…,5;j=1,2,3。b1、b2、…、b5为隐含节点的偏置权值,B 为输出节点的偏置权值。由图4可以看出,所设计的BP神经网络共包含26个参数。
第i个隐含节点的输出为
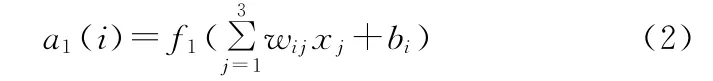
输出节点实际输出为
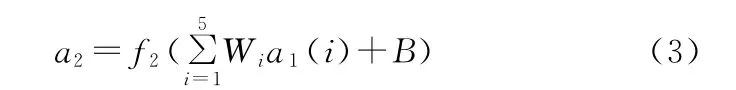
式中,f1为隐含层神经元的激活函数;f2为输出层神经元的激活函数。
误差函数为
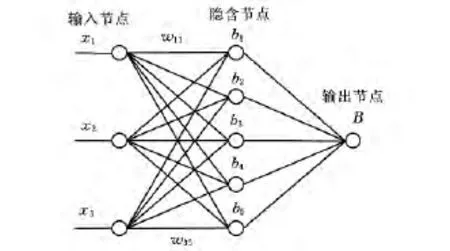
图4 磁悬浮隔振器模型ANN结构图

式中,yd为理想输出。
3 训练算法
BP算法是BP神经网络训练的常用算法,有很强的局部登山能力。但很容易陷入局部最小,得不到全局最优解。遗传算法是一种高效的全局寻优搜索算法,但局部搜索能力差。故本文利用两种算法的各自优势,提出一种混合算法,对磁悬浮隔振器动态电磁力神经网络模型的权值参数进行训练。具体思想是,先通过改进的遗传算法确定全局最优解范围,再通过BP算法,在全局最优解的范围内搜索局部最优解。
遗传算法在理论上具有全局寻优搜索能力,但是也存在一些缺点,如适应度值的标定形式多样,没有通用方法,会早熟,最优解附近左右摇摆、收敛速度慢。为了解决上述问题,本文从提高收敛速度和预防早熟两方面,对简单遗传算法进行改进,改进的具体内容是:首先,个体按照适应度的大小进行排序,保留最优解直接进入下一代,淘汰一部分的最劣解,并采用随机数补齐;然后,为了避免早熟,没被淘汰的不同个体两两进行交叉操作,形成新的个体。随着进化代数的增加,变异的比例也随之增加。这种改进的算法优点是:①各代的演化过程都保留父代中的最优个体,从而保证了可以搜索到全局最优解;②采取动态的交叉和变异比例能够有效避免早熟的发生。混合算法的具体过程包括以下几个步骤:
(1)建立遗传算法的适应度函数。适应度函数F采用系统的期望输出与实际输出差的平方来定义:

(2)产生初始种群。种群个体包含26个变量,个体采用实数编码,随机函数产生初始种群,初始种群个体数目为100,适应度函数F的精度为10-4,最佳适应度为10-4。
(3)进行选择。按照个体适应度值的大小,对群体中的所有个体进行排序,将当前种群中适应度最好的个体结构完整地复制到下一代群体中。为了保持群体中解的多样性,在选择操作中淘汰20%的最劣解,并采用随机数补齐。
(4)完成交叉与变异。采用单点交叉的形式,根据适应度值,选择交叉概率,适应度高的个体交叉和变异的几率大于适应度低的个体。为避免在接近最优解的时候出现早熟,各代之间采用动态变异率,随着代数的增加,变异率从0.02增加至0.18。
(5)实现跳转。达到指定的代数或适应度函数值时,若已寻找到全局最优解,则算法跳转到BP训练算法。
(6)寻求精确解。采用改进的BP算法在最优解范围内进行局部搜索,寻找最优解。
具体的流程如图5所示,其中,g为遗传算法实际运算代数,gmin为遗传算法实际最小适应度值,Gmin为遗传算法理论最佳适应度,Gmax为遗传算法规定的最大迭代次数,N为BP算法实际迭代次数,nmin为混合算法实际最小适应度值,Nmin为混合算法理论最佳适应度,Nmax为BP算法规定的最大迭代次数。
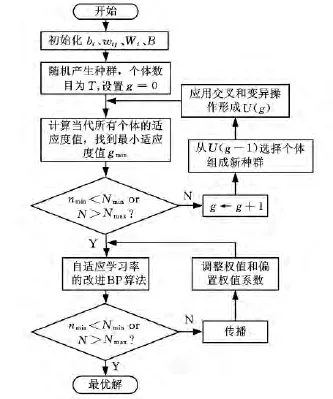
图5 混合算法流程图
4 实验结果
实验数据由图6所示的实验系统获得,输入电流频率为15Hz,实验数据分为三部分,第一部分用于设计的BP神经网络进行训练,其余两部分分别用于BP神经网络的验证和测试。

图6 磁悬浮隔振动态电磁力测量系统
利用3种训练算法得到的神经网络辨识模型的训练数据的电流误差如图7所示。首先利用训练数据,采用传统的BP算法对设计的神经网络模型训练,学习效率为0.18,经过30 000次迭代,训练得到神经网络的权值系数,该神经网络模型得到的电流与训练数据的实际电流的均方差为2.4199×10-4A,最大误差-33mA,误差比例为2.94%。接着利用训练数据,采用改进遗传算法对设计的神经网络模型进行训练,初始种群数量为100,经过200代迭代,该神经网络模型得到的电流与训练数据的实际电流的均方差仅为7.7654×10-5A,不足BP算法均方差的1/3;模型的最大误差为18.978mA,误差比例为1.69%,仅为BP算法最大误差的57%。最后利用训练数据,采用混合算法对设计的神经网络进行训练,经过改进遗传算法的150代迭代和BP算法的2 000次迭代,该神经网络模型得到的电流与训练数据的实际电流的均方差仅为7.2278×10-6A,不到BP算法均方差的3%,仅为改进遗传算法均方差的1/10;模型的最大误差为6.8679mA,误差比例为0.61%,仅为BP算法最大误差的1/5,仅略高于改进遗传算法最大误差的1/3。
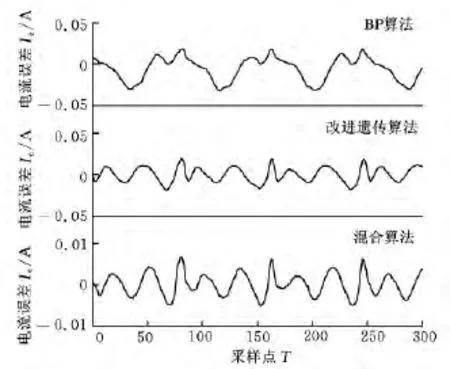
图7 3种算法模型辨识的电流误差对比(训练数据)
采用3种优化算法辨识得到的神经网络模型的输出电流与测试数据的实际电流如图8所示,对应的电流误差结果如图9所示。传统BP算法训练的神经网络得到的测试数据的均方差为1.5×10-3A,最大误差为-71.845mA,误差比例为6.30%;采用改进遗传算法训练的神经网络模型得到测试数据的均方差仅为2.0738×10-4A,仅约为 BP算法均方差的1/8;最大误差36.246mA,误差比例为3.18%,仅为BP算法最大误差的1/2。采用混合算法训练的神经网络,测试数据的均方差仅为1.5523×10-4A,约为BP算法均方差的1/10、改进遗传算法均方差的3/4;模型的最大误差-25.297mA,误差比例为2.22%,约为BP算法均方差的1/3、改进遗传算法均方差的70%。

图9 3种算法模型辨识的输出电流误差对比(测试数据)
实验结果表明:应用改进遗传算法的辨识模型的电流误差要比传统的BP算法小得多,混合训练算法的的辨识模型的电流误差最小。
5 实验验证
为验证本文设计的磁悬浮主动隔振器和提出的模型辨识方法的有效性,搭建了磁悬浮隔振实验平台。原实验台设计为双层隔振系统,为使其满足图1所示的主动隔振模型要求,需对该实验台进行改造,所采用的方法是:将实验台上层和中间层通过4个锁死支承杆固连一起,成为一个刚性结构。通过导向装置限制实验台的自由度,使之只有一个垂向自由度,如图10a所示。实验台采用B&K激振器(Modal Exciter Type 4824)进行激振,激振器的安装结构如图10b所示。力传感器测量输出力的大小,位移传感器测量位移大小,激振器力传感器测量输入力的大小。振动主动控制过程中,控制器的输入为位移传感器和力传感器等检测到的信号。控制器输出的信号通过功放,调节磁悬浮隔振器上下线圈电流的大小,产生电磁力,对产生的振动进行主动控制。本文以传递力最小作为评价指标,即输出到底座上的力越小,隔振效果越好,采用PID控制方法进行控制,控制系统结构如图11所示。其中,X为位移传感器实测位移,F为所需要的控制力,Fd为干扰力,Fe为力传感器实测电磁力,U为控制电压,I为控制电流。

图10 实验装置实物图
同等激振力下,主动系统与被动系统的输出力和力传递率如图12、图13所示。通过图12所示的对比曲线可以看出,磁悬浮主动隔振系统的输出力明显小于被动系统,谐振频率约为9.7Hz,磁悬浮主动隔振系统的输出力仅为被动隔振系统的15%,具有很好的隔振效果。通过图13对主被动隔振系统的力传递率曲线进行对比分析可以看出:在低频段,主动隔振系统隔振效果提高(力的传递率降低)了约2~3dB;系统谐振频率9.7Hz附近,系统的隔振效果提高了近15dB。
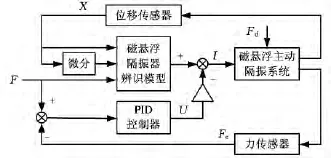
图11 磁悬浮主动隔振系统控制框图
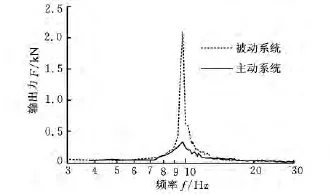
图12 主被动系统输出力对比图
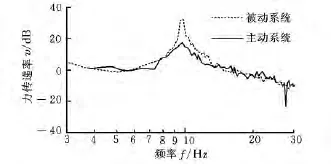
图13 主被动系统力传递率对比图
6 结语
针对磁悬浮隔振器动态电磁力的非线性及磁滞特征,本文基于BP人工神经网络的模型辨识方法建立了磁悬浮隔振器动态电磁力-气隙-电流关系的模型。采用BP算法、改进遗传算法与混合算法,对所建立的用于辨识动态电磁力的BP神经网络进行了训练。利用3种模型训练方法能较准确地获得辨识磁悬浮隔振器动态电磁力模型,采用改进遗传算法和混合算法能够提供更高的系统辨识精度,均方差和最大误差都较传统的BP算法小得多,其中,混合算法得到模型辨识精度最高,能够满足磁悬浮隔振器动态电磁力的模型辨识的需求。为了验证此辨识模型的有效性,搭建了磁悬浮主动隔振平台,建立控制模型。实验结果表明:建立的磁悬浮主动隔振系统与被动隔振系统相比,隔振效果显著提高,验证了辨识模型的有效性。
[1]Yun Y,Li Y.A General Dynamics and Control Model of a Class of Multi-DOF Manipulators for Active Vibration Control[J]. Mechanism and Machine Theory,2011,46(10):1549-1574.
[2]Shih M C,Wang T Y.Active Control of Electrorheological Fluid Embedded Pneumatic Vibration I-solator[J].Integrated Computer-aided Engineering,2008,15(3):267-276.
[3]Arzanpour S,Golnaraghi M F.A Novel Semi-active Magnetorheological Bushing Design for Variable Displacement Engines[J].Journal of Intelligent Material Systems and Structures,2008,19(9):989-1003.
[4]Daley S,Hatonen J,Owens D H.Active Vibration Isolation in a"Smart Spring"Mount Using a Repetitive Control Approach[J].Control Engineering Practice,2006,14(9):991-997.
[5]宋春生,胡业发,周祖德.差动式磁悬浮隔振系统主动控制机理研究[J].振动与冲击,2010,29(7):24-27,104.Song Chunsheng,Hu Yefa,Zhou Zude.Study on a Control Mechanism of Differential Magnetic Suspension Active Vibration Isolation System[J].Journal of Vibration and Shock,2010,29(7):24-27,104.
[6]梁青,段小帅,倪向贵,等.磁悬浮隔振器动态电磁力实验与建模[J].实验力学,2009,24(3):228-232.Liang Qing,Duan Xiaoshuai,Ni Xianggui,et al.Experiment and Modeling about the Dynamic Electromagenetic Force of a Magnetic Suspension Isolator[J].Journal of Experimental Mechanics,2009,24(3):228-232.
[7]Song Chuncheng,Hu Yefa,Xie Shengquan,et al.Dynamic Modelling of Magnetic Suspension Isolator Using Artificial Neural Network:A Modified Genetic Approach[J].Journal of Vibration and Control,2013,19(6):847-865.
