基于NCGM的粗糙表面数值模拟与实验对比

唐进元 廖东日 周 炜

中南大学高性能复杂制造国家重点实验室，长沙，410083

0 引言

很多数值方法已用于粗糙表面的模拟。Patir［1］采用线性矩阵变换方法模拟具有指定相关函数的表面，计算自相关矩阵时采用牛顿迭代法求解相关系数矩阵，该方法的主要缺点是所需的储存空间很大，计算相当费时，而且其收敛性也一直备受争议。文献［2－3］采用时间序列模型来模拟粗糙表面，采用的是自回归滑动平均模型（ARMA）。Whitehouse［4］采用自回归模型（AR）来模拟粗糙表面，但是ARMA与MA模型只考虑了低阶系统，而且只描述了原点附近的自相关函数。针对储存空间和计算速度的限制，快速傅里叶变换（FFT）方法也被用于粗糙表面的模拟。文献［5－7］采 用 FFT 方 法 模 拟 粗 糙 表 面。Wu［6－7］指出，采用FFT方法模拟粗糙表面不能同时满足正确的自相关函数与循环自相关函数，但是可以保证平均自相关函数的正确性，FFT方法只能应用于自相关长度较小的粗糙表面的模拟。基于上述文献的工作与Partir方法，为解决储存空间与计算时间的限制问题，本文采用非线性共轭梯度法［8］（NCGM）计算自相关矩阵，模拟非高斯型粗糙表面时采用Johnson转换系统［9－11］产生所需的非高斯序列。

1 粗糙表面统计规律

自相关函数可用于描述不同位置之间数据的相关程度，该函数提供了数据最基本的空间信息和数据相互之间的关系。因此，所有空间上的表面粗糙度参数都是从自相关函数获取的。

三维表面的自相关函数形式如下：

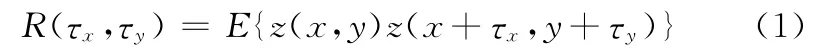
其中，E是数学期望值，τx、τy分别是x 方向、y方向的相关距离，R（0，0）即为σ2（σ为均方根）。

其离散表达式为

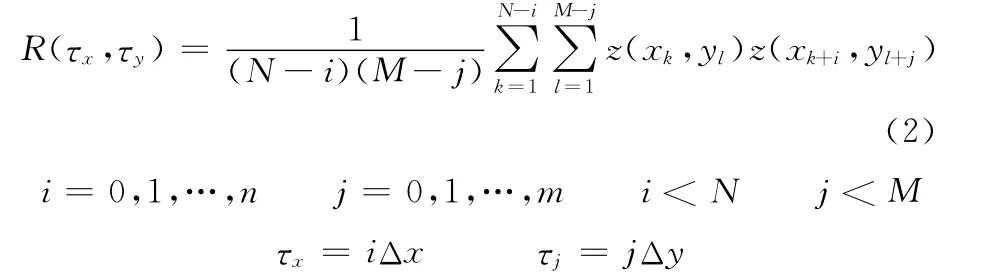
其中，n、m分别为自相关长度在x、y方向上的最大值；N、M分别为离散点沿x、y方向的总数。

相关长度τ＊定义为在轮廓方向上自相关函数衰减到临界值时的长度，Stout等［12］定义自相关函数从原点衰减到其值的10%时的长度为相关长度，此时相关函数的表达式如下：

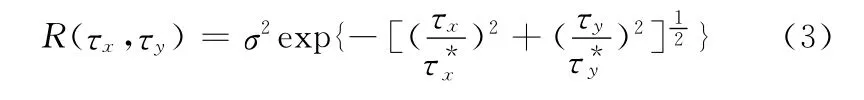
2 粗糙表面数值模拟

按高度分布函数的不同，粗糙表面可分为高斯型粗糙表面与非高斯型粗糙表面，两种粗糙表面生成的理论模型均为时间序列模型中的滑动平均模型（MA）。

2.1 高斯型粗糙表面模拟

基于Patir［1］的理论，生成（M，N）的粗糙表面需先产生（M＋m，N＋n）的独立分布的随机数和（m，n）维的自相关矩阵，生成粗糙表面的线性变换方程如下：

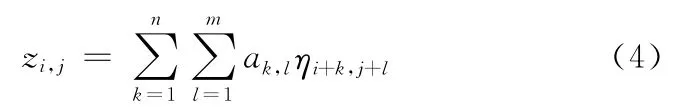
其中，ak，l是欲生成自相关函数的自相关系数矩阵第k行第l列元素，ηi，j是独立的单位方差随机数，满足以下关系式：

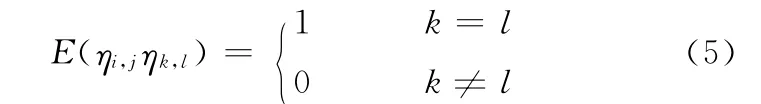
自相关函数的定义如下：

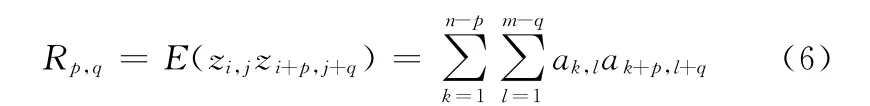
式（6）是求解维数为m×n的自相关系数矩阵的元素ak，l的非线性方程组，Patir［1］采用牛顿法求解该方程组，给定迭代的近似初值为

当用牛顿法求解式（6）时，Bakolas［13］发现，当矩阵维数一定时，该方程组不收敛。除收敛性问题外，求解式（6）的计算量相当大，还需要很大的空间来存储雅可比矩阵。

本文采用NCGM来求解该非线性方程组，把式（6）改写成：

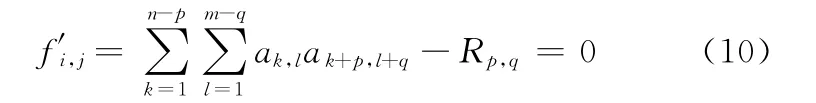
该方法把求解原函数替换成求解原函数的一阶导数。按照NCGM，现有两种搜索方向选取方法，一种为Fletcher－Reeves方法，另一种为Polak-Ribiere方法，其表达式分别为

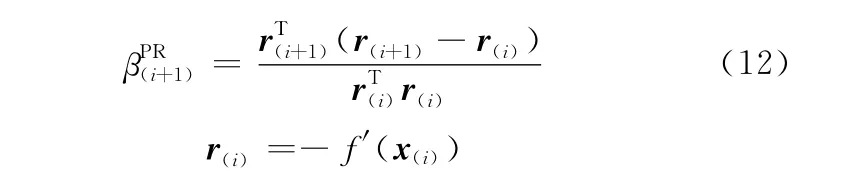
当初值选取为非常接近目标函数的解时，Fletcher－Reeves方法会收敛，而Polak－Ribiere方法在极少数情况下会不收敛，但是Polak－Ribiere方法的收敛速度比前者快很多。在迭代过程中，为避免求函数导数，采用割线法来进行非精确线搜索，其中割线法的步长需不断地调整来达到收敛，本文采用Polak－Ribiere方法求解方程组，求解步骤如下：

（2）d（0）＝r（0）－f′（x（0））（d为搜索方向）。

（3）x（i＋1）＝ x（i）＋α（i）d（i），找 到 令 f（x（i）＋α（i）d（i））最小的α（i）。

（4）r（i＋1）＝－f′（x（i＋1））。

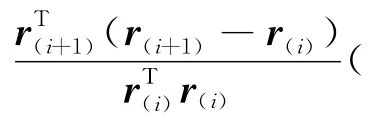
（6）d（i＋1）＝r（i＋1）＋β（i＋1）d（i）。

指定自相关函数的粗糙表面模拟步骤如下：

（1）利用计算机产生一高斯分布的随机序列μi，j。

（3）根据式（10），通过NCGM 求解得出自相关系数矩阵。

（4）根据式（4）计算得出模拟的粗糙表面z（x，y）。

基于以上理论和方法，图1和图2分别给出了相关长度βx＝βy＝3μm和βx＝βy＝10μm时的粗糙表面，粗糙表面的均值均为0，标准差为1，模拟粗糙表面点数M＝N＝60，x与y方向采样间隔均为1μm。可看出当相关长度变大时表面形貌更加缓和。当βx和βy相等时，为各向同性表面。

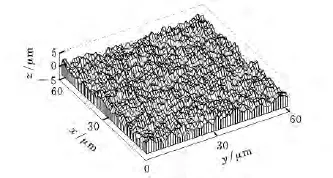
图1 相关长度βx＝βy＝3μm时的高斯分布表面

当βx和βy不相等时为各向异性表面，图3给出了βx＝30μm，βy＝3μm时的各向异性粗糙表面。当相关长度不同且数值上差别较大时，可明显看出纹理的走向。

图2 相关长度βx＝βy＝10μm时的高斯分布表面

图3 相关长度βx＝30μm、βy＝3μm时的高斯分布表面

2.2 非高斯型粗糙表面模拟

实际工程中，工程表面大多为非高斯分布表面，表面上的峰相对谷来说比较容易被除去，所以很多粗糙表面呈负偏态，故相对而言负偏态表面的接触性能较好。因此，为了更加真实地模拟粗糙表面，非高斯型表面的模拟尤为重要。粗糙表面分布的偏态为

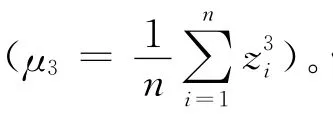
粗糙表面的峰态为

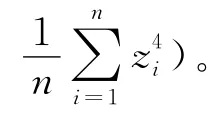
非高斯型表面的模拟相对高斯型表面来说，其输入随机序列μi，j与高斯型表面模拟时不同，模拟高斯型表面时，μi，j是高斯分布随机序列；而模拟非高斯型表面时，μi，j为非高斯分布随机序列，所以必须产生一个μi，j来满足需模拟表面的偏态与峰态。式（4）本质上是一个MA模型，对于一个纯MA模型，有

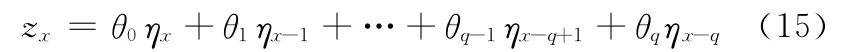
当偏态与峰态通过一个数字滤波器时，其数值会改变，所以必须对输入的偏态与峰态进行修正，其输入与输出存在以下对应关系：

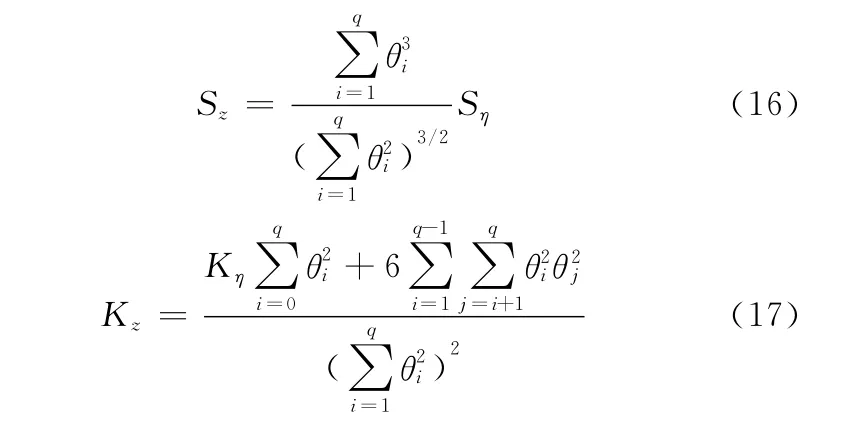
其中Sη、Kη分别为输入序列的偏态与峰态。Sz、Kz分别为输出序列的偏态与峰态，即为所求参数。根据式（4），得

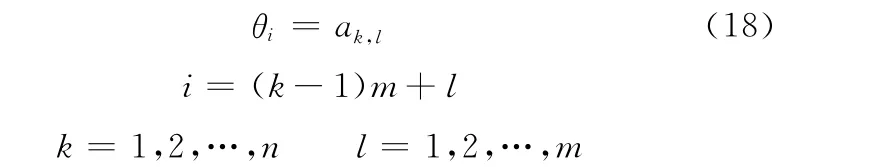
把高斯分布的随机序列转换为指定偏态与峰态非高斯随机序列需使用Johnson转换系统，按照偏态与峰态取值范围的不同，Johnson转换系统可分为SU、SL、SB三种不同的形式，在不同的偏态与峰态下有以下公式对应：

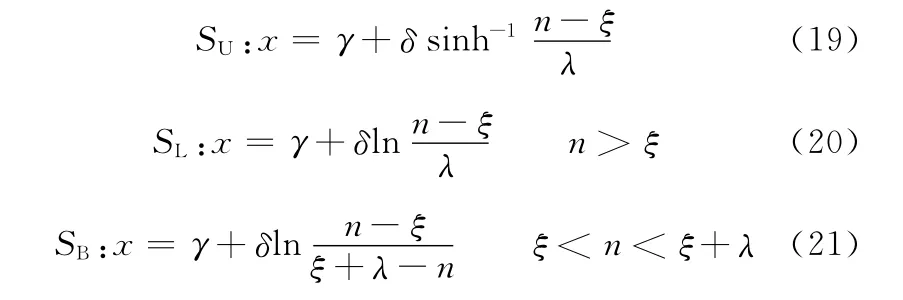
其中，SU为无界系统，SL为对数正态系统，SB为有界系统。x是标准正态分布的随机序列，η是所得到的序列。γ、δ、ξ、λ是系统得到所需偏态与峰态的4个参数。

非高斯型粗糙表面按以下步骤模拟：

（1）求解非线性方程组（式（10））。

（2）产生高斯分布序列。

（3）通过式（16）和式（17）得出指定生成的偏态与峰态序列。

（4）利用Johnson转换系统和对应系统的公式产生非高斯序列。

（5）根据式（4）产生非高斯型粗糙表面。

模拟非高斯型表面时，为了更加接近真实表面的形貌分布，采用实际加工的表面进行模拟，故自相关矩阵由真实表面计算得出。该工件采用超声磨削，磨削进给量为0.01mm，超声振动振幅为4μm，频率为20kHz，进给速度为69mm／s，砂轮转速为1440r／min，砂轮型号为 WA40L，工件材料为45钢，低温回火处理。采用Veeco Wyko NT9100光学轮廓测量仪进行表面微观形貌测量，采样间隔为0.5μm，采样点数为640×480。为减少计算量，截取其测量表面点数为60×60进行分析重构，经测量计算，x与y方向采样间隔均为4μm。

按非高斯表面模拟方法，实验扫描完整表面，实际测量区域表面与模拟的表面如图4～图6所示。可看出超声磨削加工表面有明显的加工轮廓。经计算，相关长度在y方向非常大，而x方向上的相关长度很小，完全符合加工方向的纹理分布。

图4 实验测量表面

图5 实际测量区域表面

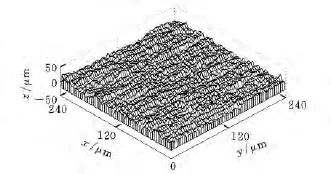
图6 模拟表面

3 粗糙表面模拟误差分析

粗糙表面模拟与理论模型要求的误差可从高度分布函数与自相关函数的对比上得出。其中高度分布函数统计主要进行均值、方差、偏态和峰态四个参数的对比，而相关函数则采用实测表面相关函数与数值模拟表面相关函数进行对比。

3.1 表面高度分布统计参数误差分析

实际加工表面的算术平均偏差Ra为0，均方根偏差Rq为6.12μm，偏态Rsk为－0.39μm，峰态Rku为3.30μm。实际加工表面与重构表面统计参数与概率密度分布曲线对比如表1、图7和图8所示。可看出两种表面在统计参数上可以很好地符合理论模型的要求。

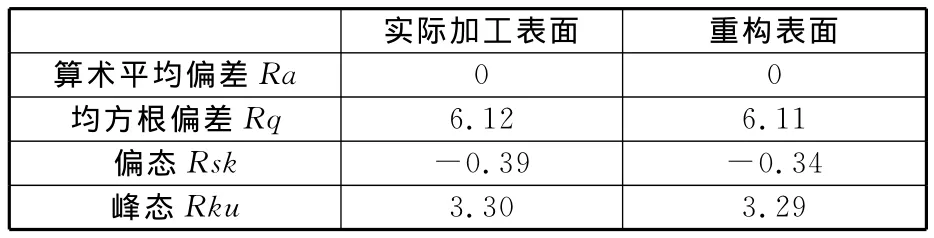
表1 实际加工表面与重构表面统计参数对比 μm

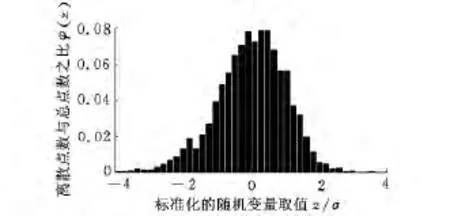
图7 实际加工表面概率密度分布

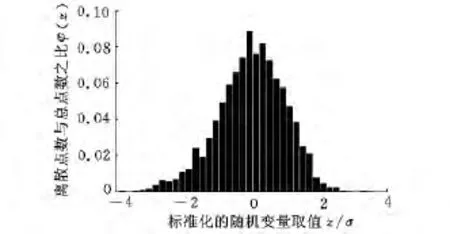
图8 重构表面概率密度分布

3.2 表面相关函数误差分析

相关函数反映的是表面各点之间的相关程度，相关函数和高度分布统计参数能完整地表征表面形貌。由于y方向相关长度很大，是主要纹理方向，故只需对比y方向自相关函数即可。实际加工表面与重构表面的自相关函数对比如图9所示，可以看出重构的表面与实际加工表面的自相关函数能较好地吻合。

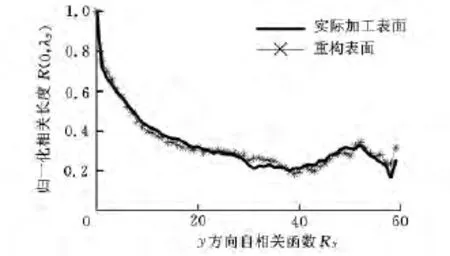
图9 实际加工表面与重构表面的相关函数

4 结语

表面高度的均值、标准差、偏态、峰态是描述高度分布函数的统计参数，而表面的相关性则用自相关函数来描述。本文采用MA模型和NCGM，能很好地克服牛顿法所带来的储存数据大、无法收敛的困难，可模拟出高度概率分布函数和自相关函数指定要求的粗糙表面。综合使用NCGM和Johnson转换系统能有效地模拟出工程表面，从而建立高精度的粗糙表面模型。

［1］Patir N.A Numerical Procedure for Random Generation of Rough Surfaces［J］.Wear，1978，47（2）：263－277.

［2］Watson W，King T，Spedding T，et al.The Machined Surface－time Series Modelling［J］.Wear，1979，57（1）：195－205.

［3］Watson W，Spedding T.The Time Series Modelling of Non－Gaussian Engineering Processes［J］.Wear，1982，83（2）：215－231.

［4］Whitehouse D.The Generation of Two Dimensional Random Surfaces Having a Specified Function［J］.CIRP Annals－Manufacturing Technology，1983，32（1）：495－498.

［5］Hu Y，Tonder K.Simulation of 3－D Random Rough Surface by 2－D Digital Filter and Fourier Analysis［J］.International Journal of Machine Tools and Manufacture，1992，32（1／2）：83－90.

［6］Wu J J.Simulation of Non－Gaussian Surfaces with FFT［J］.Tribology international，2004，37（4）：339－346.

［7］Wu J J.Simulation of Rough Surfaces with FFT［J］.Tribology International，2000，33（1）：47－58.

［8］Manesh K，Ramamoorthy B，Singaperumal M.Numerical Generation of Anisotropic 3DNon－Gaussian Engineering Surfaces with Specified 3DSurface Roughness Parameters［J］.Wear，2010，268（11／12）：1371－1379.

［9］Hill I，Hill R，Holder R.Algorithm AS 99：Fitting Johnson Curves by Moments［J］.Journal of the Royal Statistical Society Series C（Applied Statistics），1976，25（2）：180－189.

［10］Hill I.Algorithm AS 100：Normal－Johnson and Johnson－normal Transformations［J］.Journal of the Royal Statistical Society Series C（Applied Statistics），1976，25（2）：190－192.

［11］Johnson N L.Systems of Frequency Curves Generated by Methods of Translation［J］.Biometrika，1949，36（1／2）：149－176.

［12］Stout K J，Sullivan P J，Dong W P，et al.The Development of Methods for the Characterization of Roughness on Three Dimensions：EUR，0015178 EN［P］.1994－01－01.

［13］Bakolas V.Numerical Generation of Arbitrarily Oriented Non－Gaussian Three－dimensional Rough Surfaces［J］.Wear，2003，254（5／6）：546－554.