死亡率免疫理论及其在长寿风险对冲中的应用

胡仕强

(浙江财经大学金融学院，浙江 杭州 310018)

一、引 言

金融机构在未来偿还债务本金和支付利息时会产生一系列现金流，因此需要构造债券的投资组合以满足其债务偿还的承诺，即为免疫策略，更确切地说，是利率免疫策略。实施这一策略可以最大程度地降低利率变化对组合价值的影响，因此在资产负债管理中得到了广泛的研究和应用，代表性的文献有 Longstaff and Schwartz(1995)［1］和poitras and Jovanovic(2007)［2］等。同样的，寿险及年金保单的保费及准备金作为保险公司的负债也会受到利率的影响。Redington(1952)首先研究了保单负债的利率免疫问题，给出了利力变化的一阶条件:流入现金的久期应该等于流出现金的久期，即久期匹配策略［3］。之后Fisher and Weil(1971)和Shiu(1988)又拓展了Redington(1952)的免疫理论，进一步研究了单一负债和多负债免疫问题［4］［5］。这个领域较新的文献有Courtois and Denuit(2007)和Tsai(2009)等，但其关注的仍是利率风险［6］［7］。

实际上，发行寿险和年金产品的保险公司不仅要承担利率风险，而且面临死亡率和长寿风险的冲击，这对其财务状况和偿付能力都提出了更高的要求。资本市场在资金数量、流动性方面有其先天优势，因此近年来利用资本市场转移长寿风险作为一种可行的解决方案在理论和实务上都获得了长足的发展，相关文献有Hanewald(2011)［8］、Deng et al．(2012)［9］等。实务上，自2003年Swiss Re首次发行死亡率巨灾债券以来，欧美发达国家已经相继推出长寿债券、死亡率远期(q－远期)和长寿互换合同等长寿连接型金融创新产品。

与长寿风险的资本市场解决方案相比，一种被称为行业自保的长寿风险应对策略受到的关注相对较少。该方案的基本原理是利用寿险保单和年金保单对长寿风险相反的风险敞口来对冲风险。如果实际死亡率相对于预期值获得改善，寿险业务将因其死亡赔付比初始预期的延迟而获利，而年金业务将因其支付期限长于初始预期而遭受损失，因此寿险业务将成为年金业务长寿风险的一种对冲工具。相对于资本市场解决方案，自然对冲的优势是不需要一个流动性市场，可以避开长寿衍生产品发行、监管等法律和制度上的保障需求，也可以减少安排交易的成本。但是，自然对冲思想细化的一个重要问题是:在保险公司内部寿险业务和年金业务应该保持一种怎样的份额比例才能有效对冲长寿风险?本文参照Wang et al(2010)［10］拓展利率免疫理论，利用死亡率免疫理论来讨论保险公司内部寿险和年金产品的长寿风险对冲问题。

二、死亡率久期和凸性

保险公司的总负债是寿险业务的负债和年金业务的负债之和，即V=VL+VA，其中，VL是寿险业务的负债，VA是年金业务的负债，V是总负债。为了简化起见，假设一个常数的死力μ，死亡率变化对负债的影响可由Taylor展开式表示如下:

其中ε为误差项。为了达到免疫效果，当死亡率变化时，总负债不受影响，即(1)式为0，如果取一阶近似，将V=VL+VA带入并适当变形，得到:

仿照利率修正久期的定义，并考虑死亡率改善对寿险保单负债的正向关系及其对年金保单负债的反向关系，分别定义寿险负债的死亡率久期DL和年金负债的死亡率久期DA:和DA=(2)式可以变形为:

保险公司的寿险业务和年金业务的组合中，各业务保单负债在总负债中的比例只要满足(4)式，就可以利用自身内部的寿险和年金业务进行自然对冲，使未来的总负债免受死力改善，即长寿风险的影响。这样问题就归结为求寿险保单和年金保单的死亡率修正久期。为了计算方便，仿照利率近似久期的计算方法推导死亡率近似修正久期的公式。假设V0L是寿险保单的初始负债，Δμ是死力变化的绝对值，V+L表示死力下降一个很小幅度时寿险业务的新负债，V－L表示死力上升一个很小幅度时寿险业务的新负债，ΔVL是负债波动的绝对值，得到:

修正久期与债券初始价格的乘积是凸状的价格——收益率曲线在某点上的线性估计，这决定了在收益率变动不大的情况下，利用久期估计价格变化会比较准确，而在收益率变化较大的情况下，必须考虑价格——收益率曲线的凸性性质。同样道理，在死亡率变动较大的情况下，必须考虑保险公司负债——死力曲线的凸性才能更准确地预测负债变化。因此，定义死力凸性如下:表示寿险负债的死亡率凸性，表示年金负债的死亡率凸性。应用类似于久期的近似算法，可以得到死亡率凸性的计算公式:

三、死亡率免疫策略的数值分析

(一)基本假设及死亡率改善对负债的影响

假定保险公司只出售寿险和年金两种产品，并将涉及的保险产品各种定价因素约定如表1所示:

表1 保险产品的基本定价因素设定

为了研究年龄、性别和期限等的影响，对寿险产品将分别考虑30岁和40岁的被保险人，年金产品将分别考虑40岁和45岁的被保险人，男性、女性分别计算，计算20年、30年和终生保险，采用趸缴保费形式，利率稳定在3%，年金分别考虑15年延期和20年延期以考察影响死亡率久期的延期效应，定价生命表采用中国保险业经验生命表2000－2003中的CL1和CL2。

为了考察死亡率改善对寿险和年金产品负债的影响，利用CL1模拟计算死力下降10%分别对30岁男性寿险和40岁男性年金产品的负债的冲击，每种保单都考虑20年期、30年期和终生三种期限，计算结果见表2。

表2 死亡率降低10%对寿险和年金产品负债的影响

表2显示，20年定期、30年定期和终生寿险保单负债分别下降9.85%、9.65%和2.91%，寿险保单负债与死亡率变化的方向相同，且寿险保单负债的死亡率敏感性随着保险期限延长而降低;而20年期、30年期和终生年金的负债分别增加2.27%、3.31%和3.69%，即年金保单负债与死亡率变化方向相反，且其死亡率敏感性随着期限的延长而提高，终生年金受死亡率改善的冲击最大。

(二)死亡率久期和凸性的影响因素分析

与债券价格的利率敏感性受票面利率、到期时间和初始收益率三个因素的影响一样，保单负债的死亡率敏感性也会受被保险人年龄、性别、保险期限和延期期限等因素的影响。因此分别按表1对年龄、保险期限和延期期限的设定来计算死亡率久期。

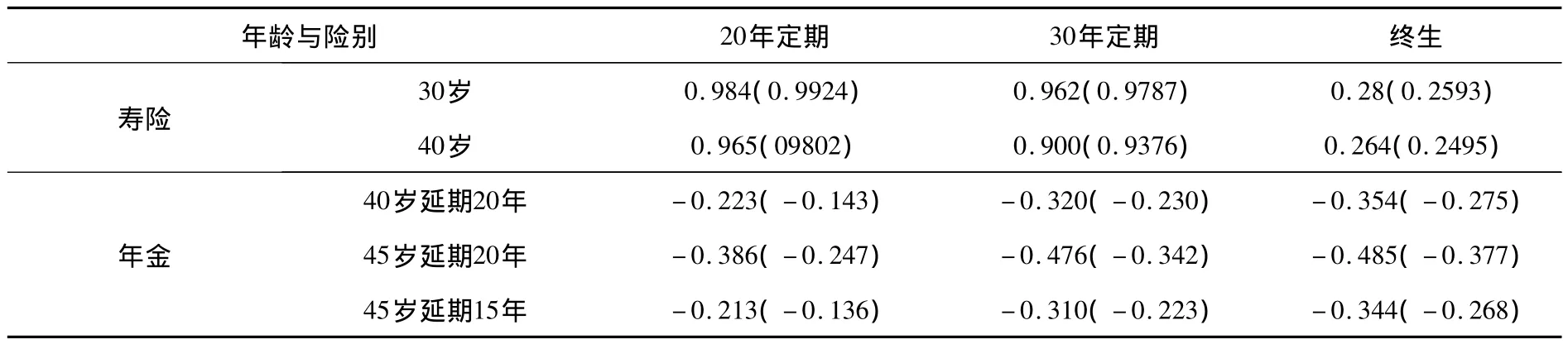
表3 死亡率久期的影响因素

表3显示:(1)寿险保单在其他条件相同时，久期将随期限的延长而减小、随年龄的增加而减小;(2)年金保单在其他条件相同时，年金的给付期限、年龄和延期年限都与久期绝对值成正向关系，且相同年限的延期效应大于年龄效应;(3)其他条件相同时，女性年金的死亡率久期绝对值均小于男性的相应值，女性寿险的死亡率久期均大于男性的相应值(终生寿险除外)。这一规律性变化对实际进行自然对冲时选择调整保单种类将具有重要的指导意义。

表3数据结合(1)式可以预测死亡率变动导致的负债变动，如对30岁男性的20年定期保险，如果仅考虑久期，则死亡率下降10%将导致负债下降9.84%，这和表2实际计算值9.85%仅相差0.01%。当然死亡率变动较大时就必须考虑死亡率凸性的影响。实际上，根据(6)式和表3，可以考察死亡率凸性的影响因素，计算结果表明死亡率凸性和死亡率久期性质相似。此外，按照表2思路可以分析凸性对保单负债变化预测的影响。如30年男性20定期保险，考虑凸性后死亡率下降10%，负债变动预测结果仅变化0.0325%。考虑到长寿风险是长期缓慢实现的，死亡率的下降不会太大，因此凸性对预测结果的影响将更小，可以忽略不计①限于篇幅，计算数据与表格分析略去。。

(三)长寿风险对冲比例

由(4)式，定义如下比例:

即当寿险负债的比例与年金负债的比例之比等于年金久期与寿险久期之比时，长寿风险得以全部对冲。

根据(7)式的最后一个等式，比例ρ可以理解成寿险业务和年金业务中达到完全的死亡率风险对冲时，两种业务的金额应满足的比例。以40岁男性年金保单为例，计算对冲一元该保单的长寿风险所需要的寿险保单的金额。为了比较对冲效果，分别计算所需的30岁男性、30岁女性、40岁男性、40岁女性不同期限寿险保单的金额。

表4 寿险与年金保单完全对冲的金额比例

表4值是寿险和年金负债组合可以免受长寿风险冲击的下限，即对冲单位金额年金保单中的长寿风险所需的最小寿险保单金额。表4结果显示，就20年期的年金而言，为了对冲年金的长寿风险，每卖出一元的年金保单，需要同时卖出0.227元的30岁男性20年定期寿险保单，或者0.232元的30岁男性30年定期寿险保单，或者0.796元的30岁男性终生寿险保单。可见，终生年金面临的长寿风险最大，而终生寿险保单对冲长寿风险的效果最不明显。

对于固定的年金保单，ρ比例将随着寿险保单的年龄和期限的增加而增加，并且女性小于男性;对于固定的寿险保单，ρ比例将随着年金保单的年龄、保险期限和延期时间而增加，同样，女性年金保单的ρ比例小于男性。

四、结论与建议

本文拓展了利率免疫理论，给出了死亡率久期和凸性的定义、计算方法，并探讨了影响保单久期和凸性的因素，结果显示:

寿险保单的久期与被保险人年龄、保险期限成反比，且女性保单的久期大于相应男性保单的久期;年金保单的久期绝对值与被保险人年龄、保险期限、延期期限成正比，且女性保单的久期绝对值小于相应男性保单的久期绝对值;死亡率凸性具有和久期一致的特性。

对于年金保单，达到长寿风险完全自然对冲的最小ρ比例将随着所选择的寿险保单被保险人的年龄和保险期限的增加而增加，且女性寿险保单的比例小于相应男性寿险保单的比例;对于寿险保单，ρ比例将随着所对冲的年金保单被保险人年龄、保险期限和延期期限的增加而增加，且女性年金保单对应的比例小于相应男性年金保单的比例。

本文虽然仅讨论了单一寿险产品和单一年金产品的久期、凸性及其对冲问题，但对于不同年龄、期限和性别等的寿险产品组合和年金产品组合，其久期、凸性也较易求得。计算方法是分别对寿险组合和年金组合中的所有产品求加权平均数，其权重就是各产品的价格占组合总价值的比重。在计算出寿险和年金产品组合的久期和凸性之后，其对冲ρ比例的计算就可以按公式(7)的方法求得。

相对于发行长寿债券、长寿互换和死亡率远期等长寿衍生产品，通过资本市场来转移长寿风险的方案，自然对冲的优势是避开了长寿衍生产品所需的发行、监管等法律和制度上的保障需求，大大降低了安排交易的成本，这对于深受长寿风险影响而又不具备发行长寿衍生产品条件的我国来说，更具有现实意义。同时，按照本文的思想，保险公司想要完全对冲其年金产品面临的长寿风险，只要有意识地调整其寿险和年金产品的销售数量和金额，获得大于或等于最低门槛值ρ的任何一个比例都可以达到目标，这给保险公司提供了足够的决策空间，不至于因对冲长寿风险而影响对寿险与年金业务比重的其他考量;即使保险公司两种业务达不到最小的ρ比例，也会产生部分对冲的效果，公司仍然可以统筹考虑其他的对冲策略来补充配合，因此自然对冲作为保险公司应对长寿风险的一种思路和选择，具有较大的灵活性和可操作性。

［1］Longstaff，F．A．，Schwartz，E．S．A simple approach to valuing risky fixed and floating rate debt［J］．Journal of Finance，1995，50(3):789－819．

［2］Poitras，G．，Jovanovic，F．Pioneers of Financial Economics，Volume 2:Twentieth Century Contributions［M］．Edward Elgar Publishing Inc．，Northampton，M．A．，2007．

［3］Redington，F．M．Review of the principles of life-office valuations［J］．Journal of the Institute of Actuaries，1952，(78):286－315．

［4］Fisher，L．，Weil，R．L．Coping with the risk of interest-rate fluctuations:returns to bondholders from naive and optimal strategies［J］．Journal of Business，1971，(44):408 －431．

［5］Shiu，E．S．W．Immunization of multiple liabilities［J］．Insurance:Mathematics and Economics，1988，(7):219 －224．

［6］Courtois，C．，Denuit，M．On immunizations and s-convex extremal distributions ［J］．Annals of Actuarial Science，2007，(2):67－90．

［7］Tsai，C．The term structure of reserve durations and the duration of aggregate reserves ［J］．Journal of Risk and Insurance，2009，76(2):419－441．

［8］Hanewald，K．Explaining mortality dynamics:The role of macroeconomic fluctuations and cause of death trends［J］．North American Actuarial，2011，15(2):290 －314．

［9］Deng，Y．，Brockett，P．and MacMinn，R．Longevity/Mortality risk modeling and securities pricing［J］．Journal of Risk and Insurance，2012，79(3):697－721．

［10］Wang，J．L．，Huang，H．C．，Yang，S．S．，Tsai，J．T．An optimal product mix for hedging longevity risk in life insurance companies:the immunization theory approach ［J］．Journal of Risk and Insurance，2010，77(2):473－497．