储层岩石微观孔隙结构特征及其对渗透率影响
2014-12-03闫国亮孙建孟刘学锋姜黎明
闫国亮,孙建孟,刘学锋,姜黎明
(1.中国石油大学地球科学与技术学院,山东 青岛266580;2.中国石油大学理学院,山东 青岛266580;3.中国石油集团测井有限公司技术中心,陕西 西安710077)
0 引 言
储层岩石的渗透率与其微观孔隙结构密切相关[1]。数字岩心作为岩石微观结构的一种数学抽象,可以更加真实地反映岩石的孔喉大小、形状和拓扑结构,提供了研究岩石微观孔隙结构和渗透率之间关系的桥梁。为研究岩石微观孔隙结构对渗透率的影响规律,首先需要对其进行定量表征。基于数字岩心主要通过提取微观孔隙空间的孔隙网络模型实现孔隙结构的定量表征。Zhao等[2]采用多向扫描方法对数字岩心孔隙空间进行多方向切片扫描搜索孔隙和喉道,但该方法很难准确探测孔隙的位置。Shin等[3]采用孔隙居中轴线方法研究了孔隙的微观结构,应用该方法可以合理分割孔隙和喉道,但是算法复杂,人机交互较多。Oren等[4-5]采用 Voronoi多面体方法提取了过程模拟法重建数字岩心的孔隙网络模型并进行了孔隙结构表征,但只适用于过程模拟法建立的数字岩心而不适用于一般数字岩心的孔隙网络建模和表征。Dong[6]采用最大球算法提取了数字岩心的孔隙网络模型,该方法建模速度较快,可用于过程模拟法和现有其他方法构建的数字岩心的孔隙网络模型建模,可以较合理区分孔隙和喉道,但确定的孔隙长度偏大而喉道长度偏小。
本文以过程模拟法重建数字岩心作为输入数据,采用改进的最大球算法提取了重建数字岩心的孔隙网络模型并对其孔隙结构进行了定量表征;研究了孔隙半径和喉道半径等微观孔隙结构参数对渗透率的影响规律。
1 数字岩心重建
X射线CT法是建立数字岩心最直接、最准确的方法,但由于实验成本过高,限制了该项技术的广泛应用。一般采用数值重建算法得到数字岩心。数值重建算法是通过岩心二维薄片的统计分析,得到孔隙度、两点相关函数、粒度分布等统计信息和黏土含量、矿物组成等岩石特性,利用这些信息重建数字岩心。数值重建方法主要有随机法和过程模拟法2种。随机法包括高斯场法[7],模拟退火法[8-9],顺序指示模拟法[10-12],多点地质统计法[13-15]和马尔可夫链法[16]。当孔隙度较小时,除多点地质统计法和马尔可夫链法之外,随机法重建数字岩心的孔隙连通性较差。过程模拟法通过模拟岩石的形成过程重建数字岩心,包括沉积过程、压实过程和成岩过程的模拟。Oren和 Bakke[5,17]应用该方法建立了Fontainebleau砂岩和Berea砂岩的数字岩心,与对应的X-CT扫描得到的数字岩心的渗流属性计算结果比较表明,过程模拟法建立的数字岩心可以重现真实岩心的孔隙结构和连通特性。笔者采用Oren等提出的过程模拟方法,以某地区砂岩(称为S1砂岩)岩心的二维薄片为基础,应用自主开发的过程模拟法程序重建了该砂岩的数字岩心。
S1砂岩的二维薄片如图1所示。图1中白色部分为岩石颗粒,黑色部分为孔隙。采用过程模拟法重建S1砂岩的数字岩心结果如图2(a)所示,图2中蓝色部分为岩石骨架,红色部分为孔隙空间。

图1 S1砂岩岩心的二维薄片

图2 S1砂岩的数字岩心及其孔隙网络模型示意图
2 孔隙网络模型提取及孔隙结构定量表征
2.1 孔隙网络模型提取
基于过程模拟法重建的S1砂岩的数字岩心应用改进的最大球算法提取数字岩心的孔隙网络模型。首先对涉及到的基本概念进行解释。
体素:在三维空间中,用以进行空间信息的数据记录、处理、表示等所采用的具有一定大小的最小体积单元。
孔隙体素:数字岩心中表示孔隙部分的最小体积单元。
骨架体素:数字岩心中表示骨架部分的最小体积单元。
内切球:以孔隙体素为球心向四周等速延伸,直到碰到最近的骨架体素,延伸区域中所有体素的集合。
冗余球:设B表示内切球,如果存在A为任一内切球,使得B⊂A,则称B为冗余球。
最大球:设所有内切球的集合用I表示,冗余球的集合用M表示,则I-M为最大球集合,其中每个元素称为最大球。任意一个最大球至少包含1个其他最大球没有的体素。
Dong等[6]提出的最大球算法存在的主要问题是提取的孔隙网络模型的孔隙长度偏大而喉道长度偏小,间接影响其他孔喉参数的确定且计算的渗透率偏大。笔者针对这一问题,采用计算机图形处理学中的几何变换技术和应用统计学中的判别分析方法,确定孔隙网络模型的孔隙长度和喉道长度,从而确定孔隙和喉道的其他参数。
改进后的最大球算法提取数字岩心孔隙网络模型的主要步骤为:
(1)搜寻内切球。基于数字岩心,首先采用扩张算法,从第1个孔隙体素开始,以其为中心,从26个方向(见图3,红色方块表示孔隙体素,灰色方块表示与其相邻的26个体素)寻找距离最近的骨架体素,然后以找到的骨架体素与孔隙体素的距离为最大范围,采用收缩算法逐一检查该范围内的体素,确定该孔隙体素对应的内切球。
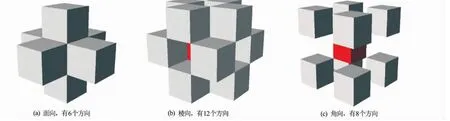
图3 孔隙体素的26个搜索方向
采用相同方法寻找下一孔隙体素的内切球,直到所有孔隙体素都被遍历,即可得到所有孔隙体素对应的内切球集合。
(2)删除冗余球。设A和B分别为内切球,它们的球心和半径分别为CA、CB、RA和RB,且RA>RB,如果满足条件
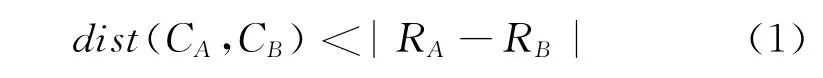
则球B为冗余球,从内切球集合中删除。式(1)中dist(CA,CB)表示内切球A和球B两者球心的距离。
采用上述判别法则从内切球集合中删除所有冗余球。
(3)孔隙喉道识别。去掉冗余球的内切球集合称为最大球集合,应用排序算法和成簇算法[6]识别孔隙和喉道。采用排序算法将最大球集合中的所有元素按照半径从大到小排序,根据半径将其划分为一系列的子集,每一个子集中最大球的半径相同。对每一子集中的最大球采用成簇算法确定其属于孔隙或喉道并得到相应的孔隙和喉道的半径。
(4)孔隙网络模型参数计算。对于每一个孔隙,以该孔隙对应的最大球球心体素为原点,选择过该孔隙中心体素的任一直线作为旋转轴。设平面β绕该旋转轴每隔一定角度旋转,直到转过180°。应用几何变换技术可以得到平面β对该孔隙局部空间剖切的剖面。在剖面内每隔一定角度发出1条射线,用于测量该方向上孔隙中心体素到岩石骨架体素的距离。对记录的所有距离应用判别分析方法确定出孔隙的长度。确定孔隙长度后即可确定孔隙的体积、形状因子(形状因子是指孔隙或喉道截面面积与其周长平方之比)和喉道的长度等参数。喉道体积及形状因子的确定方法与孔隙体积及形状因子的确定方法类似。
采用改进的最大球算法提取的S1砂岩数字岩心的孔隙网络模型[见图2(b)],用球表示孔隙,管表示喉道。根据形状因子的不同,实际计算中孔隙网络模型的孔隙和喉道均为不同截面形状的柱体。
2.2 孔隙结构定量表征
基于孔隙网络模型,统计孔隙半径和喉道半径的频率分布,得到S1砂岩数字岩心的孔隙结构参数分布图(见图4和图5)。由于缺少S1砂岩的恒速压汞实验数据,因此得到的孔隙结构参数分布没有与实验数据对比,但经过数据拟合分析,S1砂岩数字岩心的孔隙半径和喉道半径等微观孔隙结构参数满足对数正态分布,这种分布特征与Morrow[18]得到的结论一致。

图4 S1砂岩数字岩心的孔隙半径频率分布
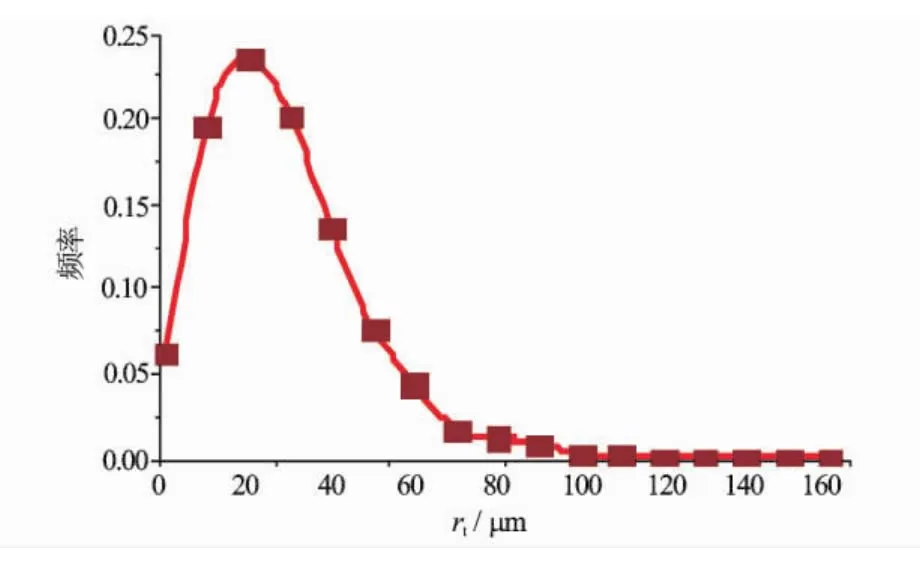
图5 S1砂岩数字岩心的喉道半径频率分布
3 渗透率数值模拟
应用逾渗网络理论[19]可求得孔隙网络模型i方向(可取x,y,z)的流量,根据Darcy定律计算渗透率

式中,Ki为孔隙网络模型i方向的渗透率,mD*非法定计量单位,1mD=9.87×10-4μm2,下同;Li为i方向长度,cm;Ai为i方向截面积,cm2;pI-pO为i方向压差,×10-1MPa;μ为流体黏度,mPa·s;Qi为i方向流量,cm3/s。
通过对比S1砂岩实验测量的渗透率和改进后最大球算法提取的孔隙网络模型计算的渗透率评价上述方法的准确性。S1砂岩实验测量的孔隙度为19.70%,平均渗透率为1 286mD。S1砂岩孔隙网络模型的孔隙度为19.78%,计算的平均渗透率为1 362mD,与S1砂岩实验测量结果接近,说明了该方法的正确性。同时,原有最大球算法提取的S1砂岩的孔隙网络模型的孔隙度为19.78%,计算的平均渗透率为1 531mD,与改进后的结果相比,改进后最大球算法提取的孔隙网络模型的渗透率更接近实验测量结果。
根据孔隙结构表征部分孔隙半径和喉道半径频率分布,采用式(3)计算得到渗透率贡献值曲线[20]

式中,ΔKj为第j个区间的渗透率贡献值;rj为第j个区间的孔隙或喉道半径值;αj为第j个区间的孔隙半径或喉道半径频率。
选取渗透率贡献最大值对应的孔隙半径和喉道半径作为S1砂岩孔隙和喉道半径的特征值。分别改变孔隙网络模型的孔隙半径分布和喉道半径分布,得到图6和图7所示的S1砂岩的孔隙半径特征值和喉道半径特征值与渗透率的关系曲线。可见喉道半径特征值对渗透率的影响大于孔隙半径特征值对渗透率的影响。渗透率随孔隙半径特征值和喉道半径特征值的变化规律均可以用Logistic函数关系描述

式中,K为渗透率,mD;r为孔隙半径或喉道半径特征值,μm;c为曲线趋于稳定段的渗透率,mD;a为渗透率快速增加段中点对应的孔隙半径或喉道半径特征值,μm;p表征渗透率随孔隙半径或喉道半径特征值变化的快慢,取值一般在2~3之间,无量纲。
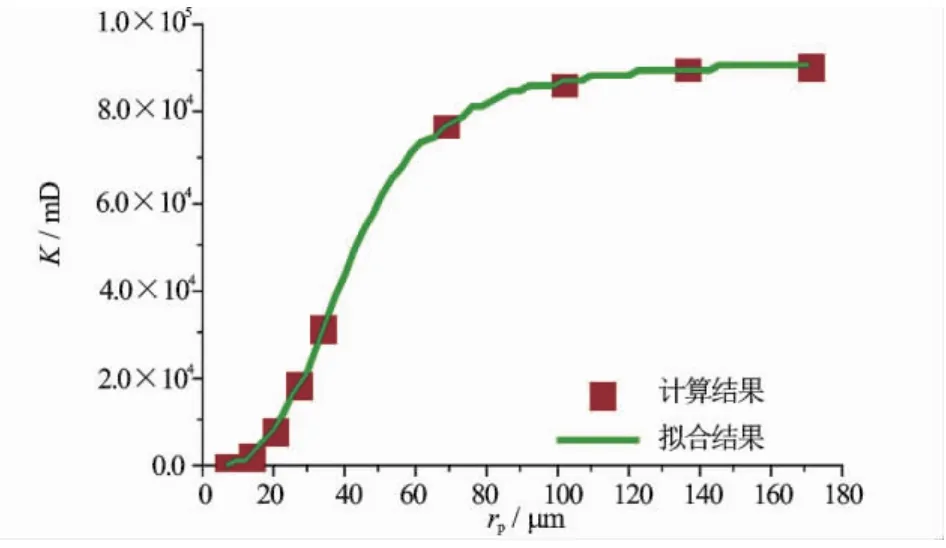
图6 S1砂岩孔隙半径特征值与渗透率关系

图7 S1砂岩喉道半径特征值与渗透率关系
4 结 论
(1)在岩心二维薄片的基础上,采用过程模拟法重建的数字岩心不仅能够反映岩石的微观孔隙结构特征,而且具有与真实岩心相近的渗流特性。
(2)通过孔隙半径和喉道半径等孔隙结构参数的定量表征,表明S1砂岩微观孔隙结构参数的分布基本满足对数正态函数分布。
(3)S1砂岩的孔隙半径和喉道半径特征值与渗透率之间的关系可以用Logistic函数关系描述,且喉道半径特征值对渗透率的影响大于孔隙半径特征值对渗透率的影响。
[1] Dullien F A.Porous Media Fluid Transport and Pore Structure[M].New York:Academic Press,1992.
[2] Zhao H Q,Macdonald I F,Kwiecien M J.Multi-orientation Scanning:A Necessity in the Identification of Pore Necks in Porous Media by 3-D Computer Reconstruction from Serial Section Data [J].Journal of Colloid and Interface Science,1994.162(2):390-401.
[3] Shin H,Lindquist W B,Sahagian D L,et al.Analysis of the Vesicular Structure of Basalts[J].Computers and Geosciences,2005,31:473-487.
[4] Bakke S,Oren P E.3-D Pore-scale Modeling of Sandstones and Flow Simulations in the Pore Networks[C]∥SPE 35479,1997.
[5] Oren P E,Bakke S.Reconstruction of Berea Sandstone and Pore-scale Modeling of Wettability Effects[J].Journal of Petroleum Science and Engineering,2003,39(3-4):177-199.
[6] Dong H.Micro-CT Imaging and Pore Network Extraction[D].London:Imperial College,2007.
[7] Joshi M.A Class Three-dimensional Modeling Technique for Studying Porous Media[D].Kansas:University of Kansas,1974.
[8] Hazlett R D.Statistical Characterization and Stochastic Modeling of Pore Networks in Relation to Fluid Flow [J].Mathematical geology,1997,29(6):801-822.
[9] 赵秀才,姚军,陶军,等.基于模拟退火算法的数字岩心建模方法 [J].高校应用数学学报:A辑,2007,22(2):127-133.
[10] Keehm Y.Computational Rock Physics:Transport Properties in Porous Media and Applications[D].Stanford:Stanford University,2003.
[11] 朱益华,陶果.顺序指示模拟技术及其在3D数字岩心建模中的应用 [J].测井技术,2007,31(2):112-115.
[12] 刘学锋,孙建孟,王海涛,等.顺序指示模拟重建三维数字岩心的准确性评价 [J].石油学报,2009,30(3):391-395.
[13] Okabe H,Blunt M J. Pore Space Reconstruction Using Multiple-point Statistics[J].Journal of Petroleum Science and Engineering,2005,46:121-137.
[14] 张挺,卢德唐,李道伦.基于二维图像和多点统计方法的多孔介质重构研究 [J].中国科技大学学报,2010,40(3):271-277.
[15] 张丽,孙建孟,孙志强,等.多点地质统计学在三维岩心孔隙分布建模中的应用 [J].中国石油大学学报:自然科学版,2012,36(2):105-109.
[16] Wu K,Nunan N,Crawford J W,et al.An Efficient Markov Chain Model for the Simulation of Heterogeneous Soil Structure [J].Soil Science Society of America,2004,68:346-351.
[17] Oren P E,Bakke S.Process Based Reconstruction of Sandstones and Predictions of Transport Properties[J].Transport in Porous Media,2002,46(2-3):311-343.
[18] Morrow N R.Interfacial Phenomena in Petroleum Recovery[M].New York:Marcel Dekker Inc,1991.
[19] Valvatne P H.Predictive Pore-scale Modeling of Multiphase Flow[D].London:Imperial College,2004.
[20] 罗蛰潭,王允诚.油气储集层的孔隙结构 [M].北京:科学出版社,1986.
