随钻方位电磁波仪器界面预测影响因素分析

杨锦舟

（中石化胜利石油工程有限公司钻井工艺研究院，山东 东营257000）

0 引 言

随钻电磁波电阻率以及随钻方位电磁波仪器在地层界面、油水界面预测和判断方面有着重要应用。较大的探测深度能提早预知地层界面，从而及时调整钻头方向，避免钻后调整。随钻电磁波电阻率与随钻方位电磁波电阻率的仪器结构和工作频率不同，探测深度也不同。常规的随钻电磁波电阻率仪器多采用多频率、多线圈距解决探测深度与垂直分辨率之间的矛盾，随钻方位电磁波仪器则在多频、多线圈距的基础上增加了多分量测量，使之具备方位特性。随钻电磁波电阻率与随钻方位电磁波仪器的探测深度有不同的定义，本文模拟随钻方位电磁波仪器的界面响应特征，分析随钻电磁波电阻率与随钻方位电磁波探测深度的不同意义和影响因素，以及各种因素对界面距离反演结果的影响，为准确预测和判断地层界面提供理论依据。

1 方位电磁波仪器探测原理及模拟方法

传统的随钻电磁波电阻率仪器发射和接收线圈都采用轴向线圈，测量信号与仪器工具面角方位角［1］无关（本文中，仪器工具面方位角也用来表示接收线圈的磁矩方位），不具备方位特性。采用倾斜或横向的发射或接收线圈，测量信号则具备方位特性［2－3］，这一性质拓宽了随钻电磁波仪器在地质导向中的应用。当仪器接近或远离储层界面时，传统的电磁波电阻率仪器无法确定储层界面方位，给钻头调整带来了不确定性，随钻方位电磁波仪器则可以较好地解决这个问题［4］。

在图1所采用模型中，发射线圈与接收线圈分别垂直或平行，仪器与地层界面平行，仪器旋转过程中，接收线圈的磁场分量Hij，（i，j＝x，y，z）随仪器工具面角相对变化如图1所示，i、j分别为发射线圈和接收线圈磁矩方向。可以看出磁场的9个分量中（实部和虚部），除了Hzz外，其余分量均具备方位分辨能力，而Hzz一般用来测量地层电导率。其中Hxz、Hzx、Hyz、Hzy周期为2π，Hxx、Hyy、Hxy、Hyx周期为π。这说明利用Hxx、Hyy、Hxy、Hyx分量无法直接区分相差180°的地层方位变化，所以在传统的随钻电磁波电阻率的基础上只需增加1个倾斜或横向接收发射（发射）线圈，即可实现对地层的方位识别。传统的随钻电磁波电阻率仪器一般只测量电磁场的ZZ分量，而随钻方位电磁波电阻率则实现了多分量测量。

本文采用的计算模型中发射线圈的磁矩与仪器轴重合（见图2），接收线圈磁矩相对于仪器轴存在45°夹角。假设大地坐标系为xyz，仪器轴与地层法线夹角为α，方位角为β（相对于x轴），接收线圈磁矩与仪器轴线所在垂面的夹角为γ。仪器坐标系为x′y′z′，大地坐标系与仪器坐标系之间的磁矩存在转换关系

图1 随钻方位电磁波测量磁场分量随仪器工具面变化关系

式中，

图2 仪器坐标系与大地坐标系关系示意图

根据麦克斯韦方程［5］可以模拟仪器周围电磁场分布规律

式中，H、E分别是磁场强度和电场强度；Js为源电流密度；Ji为感应电流密度；ω为角频率；ε为介电常数；μ0＝4π×10－7（H／m）；σ′为复电导率张量，σ′＝σ＋iωε。为了简便计算，假设发射天线和接收天线的磁矩均在平面XOZ内，即（β＝0），磁矩方向与仪器轴之间的夹角分别为θT、θR＝45°。将天线简化为磁偶极子，应用并矢格林函数可以得出任意方向磁偶极子的电磁场分量［6］，接收线圈处的磁场根据所处的位置可以认为是入射波、反射波以及透射波的叠加，接收线圈处磁场的x分量和z分量分别为［7］

式中，Gij（i，j＝x，z）表示i方向单位磁偶极子源产生磁场强度的j分量。将界面定向信号幅度定义为接收线圈方位角分别为0°和180°（相对于地层界面）的2个方向测量信号幅度的差别［8］。即

本文中主要考虑发射－接收天线对之间的界面定向信号幅度衰减。

2 随钻方位电磁波仪器界面响应与界面方位判断

2.1 界面响应模拟

图3是界面两侧地层电阻率分别为1Ω·m和10Ω·m，哈里伯顿公司深方位电磁波仪器ADR以接近水平姿态穿过地层界面（仪器轴与地层法线夹角为85°），线圈距为48in＊非法定计量单位，1in＝25.4mm，下同的仪器响应模拟曲线。可以看出在该地层条件下，方位电磁波仪器的定向幅度曲线在其2MHz和500kHz等2种工作频率下，对地层界面都有良好的指示和预测作用，随着仪器距离地层界面越来越近，响应幅度信号也越来越大，根据方位电磁波仪器的这一响应特点，利用马奎特方法对其响应进行反演计算，可以得到仪器与地层界面的距离［9］，除此之外，方位电磁波定向曲线还能判断出地层界面的方位，是位于仪器的上方还是下方，从而指导调整钻头钻进方向。而常规的随钻电磁波电阻率仪器，在该地层条件下，无论是仪器从下方还是上方接近和穿过层界面，仪器响应都是相同的，从而无法进行准确的地质导向。

2.2 层界面方位判断

采用横向或倾斜的接收线圈时，接收线圈的定向幅度响应信号随着仪器工具面变化呈现周期变化（见图1），当只有发射或接收线圈倾斜时（即测量Hxz、Hzx、Hyz、Hzy分量时），信号周期为2π。利用工具面角与定向信号幅度的关系可以确定地层界面的相对方位。模拟地层界面与水平面的夹角分别为0°、90°和180°，井眼与层界面平行情况下，仪器工具面角与仪器定向幅度信号的关系，其中井眼与层界面的相对方位关系如图4所示。可以看出当地层界面与接收线圈磁矩所在平面垂直时（接收线圈位于界面的正上方或正下方，即0°方位角），定向幅度信号为极大值或极小值，地层界面走向与接收线圈磁矩平行时，定向幅度信号为0，因此随着地层界面方位的变化，定向信号幅度极值点对应的工具面角随之变化，而极值点对应的工具面方位角与界面的相对方位是一致的，利用这一性质可以判断地层界面的相对方位。

3 探测深度的定义与界面响应模拟

图3 方位电磁波电阻率仪器穿过地层界面时的响应情况

图4 定向幅度信号随仪器工具面角变化规律

探测深度的概念最早来源于描述感应测井的Doll几何因子理论［10］，也指探测直径（半径），而Doll几何因子理论的应用有2个前提：仪器周围介质具备旋转对称性；仪器工作频率足够低，以至于能忽略趋肤效应的影响。在该条件下，几何因子被用来表示仪器周围不同径向范围内的信号贡献率。通常把径向积分几何因子为50%的径向半径定义为仪器的探测深度。对于常规随钻电磁波电阻率仪器来说主要是利用了电磁波的趋肤效应测量接收线圈的幅度比和相位差，因此严格说不能用几何因子理论定义探测深度。随钻电磁波电阻率仪器仍然借用了Doll几何因子的概念，但其探测深度不是某一固定值，而是与地层电阻率以及泥浆电阻率有关。在其他条件一定的情况下，地层电阻率越大，电磁波电阻率仪器探测深度越大［11］。

方位电磁波仪器常用来探测和识别地层界面，其探测深度用来表示对界面的探测能力，而存在地层界面的模型中无法用Doll几何因子理论描述仪器探测深度的问题。目前对于随钻方位电磁波仪器的探测深度尚没有标准的定义，国外各服务公司或仪器研发厂家常用仪器对边界存在引起的信号变化的探测能力定义探测深度［12］。因此，仪器对边界探测能力依赖于仪器对小信号的识别能力以及实际的地层模型。对于采用倾斜接收线圈随钻方位电磁波仪器来说，电磁场采用了多分量测量，其界面定向信号幅度也可表示为［13］

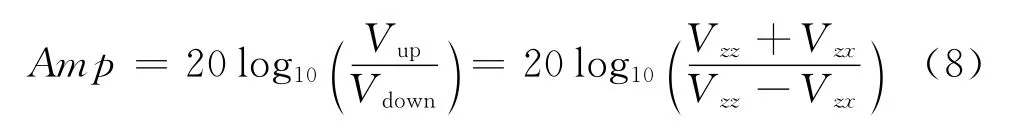
利用接收线圈相对地层界面上、下2个方向的测量电动势的比值指示界面。式（8）中，Vup、Vdown分别为线圈相对地层界面上、下2个指向的电动势，Vij（i，j＝x，y，z）表示为接收线圈的电动势，其中i为发射线圈指向，j为接收线圈指向。

如果表示成以e为底的对数，即

当Vzx≪Vzz时

由图1可知，磁场分量ZZ不具备方位特性，方位特性的区分取决于交叉耦合磁场分量ZX，交叉耦合磁场分量ZX在均匀介质中为0，在靠近地层界面时，磁场分量ZX逐渐增大，磁场分量ZZ在均匀介质中为与地层电导率相关的定值，在远离地层界面时Vzz≫Vzx。因此对磁场分量ZX的探测和分辨能力决定了仪器的探测深度。图5为模拟接收线圈磁场分量ZZ激发的电动势幅度以及交叉耦合磁场分量ZX激发的电动势幅度随界面距离的变化关系，数值模拟所采用的地层模型如图3（a）所示，相邻地层电阻率分别为1Ω·m和10Ω·m，线圈距为112in，工作频率为500kHz。由模拟结果看，同轴耦合磁场分量ZZ激发的电动势幅度比交叉耦合磁场分量ZX激发的电动势幅度在远离界面处要高2～3个数量级，因此由式（9）可得，对磁场分量ZX的分辨能力越强，界面定向幅度信号的分辨率也就越高，界面探测深度越大。

图5 同轴磁场分量ZZ激发电动势和交叉耦合分量ZX激发电动势随地层界面距离变化关系模拟

4 探测深度影响因素分析

4.1 工作频率

采用地层模型如图3（a）所示，上下地层电阻率分别为1Ω·m和10Ω·m。仪器以接近水平姿态穿过地层界面，分别模拟不同频率和线圈距情况下的仪器响应情况。图6为模拟哈里伯顿公司仪器ADR线圈距112in，工作频率分别为2MHz、500、125、80、20kHz时的仪器响应，可以看出除了2MHz响应曲线在界面处出现异常，随钻方位电磁波仪器在界面处的响应幅度随工作频率的降低而减小，在仪器灵敏度一定的情况下（假设0.02dB），2MHz、500以及125kHz频率下仪器的探测深度随频率的降低而增加，而频率继续降低时，仪器探测深度增加不明显甚至降低（工作频率20kHz），也就是说不能单纯靠降低工作频率增加仪器探测深度。

4.2 线圈距

图7为模拟在一定工作频率下（125kHz）不同线圈距的仪器界面响应。由模拟结果可看出，仪器界面响应相对幅度随着线圈距的增大而增大，在同样的灵敏度情况下，线圈距越大，仪器探测深度越大，但随着线圈距的增大，探测深度增加的幅度越来越小，而且增加仪器长度会对仪器使用带来很大限制和不便，因此也不能无限增大线圈距来提高探测深度。值得注意的是，线圈距越大，相对信号幅度越大，这是由于感应电动势Vzz的幅度随着线圈距的增大而降低（见图8），但感应电动势Vzx幅度在距离界面一定位置后却随着线圈距的增大而增大，这造成了线圈距越大，界面定向信号幅度越大（见表1）。

图6 不同工作频率时的仪器响应

图7 相同频率不同线圈距时的仪器响应

4.3 地层电阻率（电导率）对比度

图8 不同线圈距时的同轴电动势ZZ和交叉耦合电动势ZX幅度相对关系

表1 不同界面距离处的同轴电动势ZZ和交叉耦合电动势ZX相对幅度值

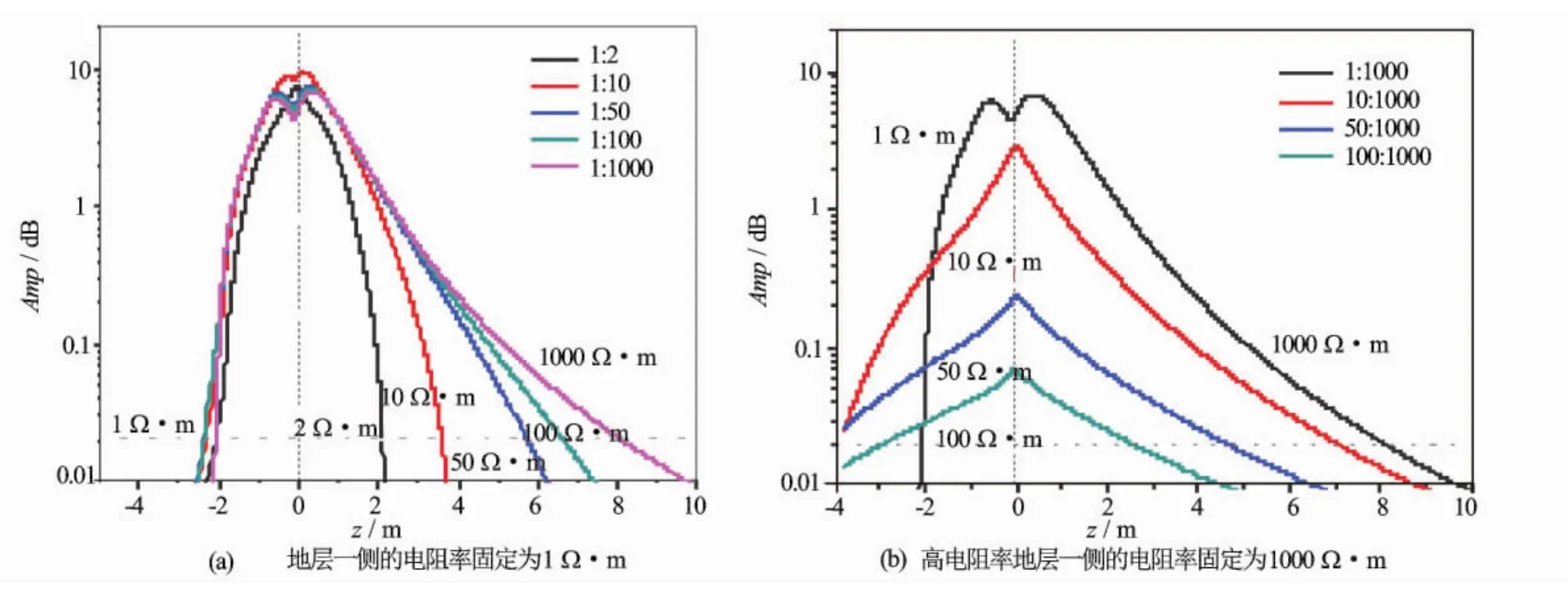
图9 不同电阻率对比度情况下的仪器响应及探测深度

针对图3地层模型，界面一侧电阻率固定为1Ω·m，模拟地层电阻率对比度分别为1∶2、1∶10、1∶50、1∶100和1∶1 000时的仪器响应［见图9（a）］。可以看出相同信号灵敏度的情况下（0.02dB），电阻率对比度越大，仪器对高电阻率地层的探测深度越大，探测深度从2m可达到8m，而对低电阻率地层探测深度影响不大。图9（b）为固定相对高电阻率地层电阻率1 000Ω·m不变，另一侧电阻率分别为1、10、50和100Ω·m，此时仪器对相对高电阻率地层的探测深度主要受电阻率对比度影响，电阻率对比度越高，仪器探测深度越大。而对相对低电阻率地层的探测深度则受地层电阻率和电阻率对比度双重因素的影响，相对高的地层电阻率会增加探测深度，但会降低电阻率对比度，从而影响到仪器的探测深度，由模拟结果看出在固定低电阻率地层的电阻率时，相邻地层电导率的差变化不大，在一个数量级范围内（500～999mS／m），相应的界面响应幅度变化也不大，而固定高地层电阻率时，相邻电导率变化范围大约为3个数量级（10～999mS／m），相应的界面响应幅度变化也较大，因此相邻地层电导率的差是决定方位电磁波界面响应幅度的重要因素。

5 地层界面距离反演效果影响分析

在地质导向应用中，主要通过对随钻方位电磁波实时资料的反演预测地层界面距离。在分析了方位电磁波探测深度的影响因素后，模拟这些因素对界面距离反演结果的影响，常用的模型为2层或3层地层模型。将测井数据表示为向量形式，地层参数与仪器响应可以表示为

式中，R为相邻地层电阻率，可以通过邻井资料或随钻测井资料得到；h为仪器到地层界面的距离；y为随钻方位仪器响应值；f为仪器响应函数；Φ为目标函数。该反演的过程就是通过逐次修正h实现Φ最小化的过程。马奎特反演计算方法作为一种局部最优算法，局限性在于局部收敛，反演计算时初始值的选取尽可能多地结合已有的地层信息，使初始值的选取更加合理。反演计算过程中通过利用误差与设定最小误差控制反演结果。图10为对界面距离反演的效果对比，采用2层地层模型，1 000m处为地层界面，界面两侧电阻率分别为1Ω·m和20Ω·m，对哈里伯顿公司仪器ADR 112in线圈距、125kHz的响应曲线进行反演，预测仪器与界面距离。其中图10（a）中分别设定仪器分辨率为0.02dB和0.05dB，图中标出了真实界面距离10%的误差线，可以看出，随着距离的增大，反演结果的误差也越来越大，该算例中分辨率为0.02dB时反演得到的有效界面距离大于5m，远大于分辨率0.05dB时反演得到的有效界面距离，因此仪器对小信号的分辨能力越高，反演距离结果越可靠。图10（b）针对电阻率分别为1Ω·m和20Ω·m的响应进行反演，在反演过程中，高电阻率层的电阻率采用30Ω·m，由反演结果可知增大高电阻率地层的电阻率在层界面3m以内，对界面距离的反演结果基本没什么影响，随着界面距离的增大，反演得到的距离与真实界面距离的偏差越来越偏大。反演过程中，如果增大低电阻率地层的电阻率，保持电阻率对比度不变，例如在本算例中低电阻率层电阻率由1Ω·m增大到1.5Ω·m，则导致在地层界面附近反演结果比实际界面距离偏小，随着界面距离增大，反演结果与真实距离越来越接近。考虑到仪器对小信号分辨率的问题，越远离界面信号越小，反演结果越不可靠，因此在地层界面距离反演过程中，高电阻率地层电阻率值不准确对反演结果影响不大，关键要确定好低电阻率地层的电阻率。

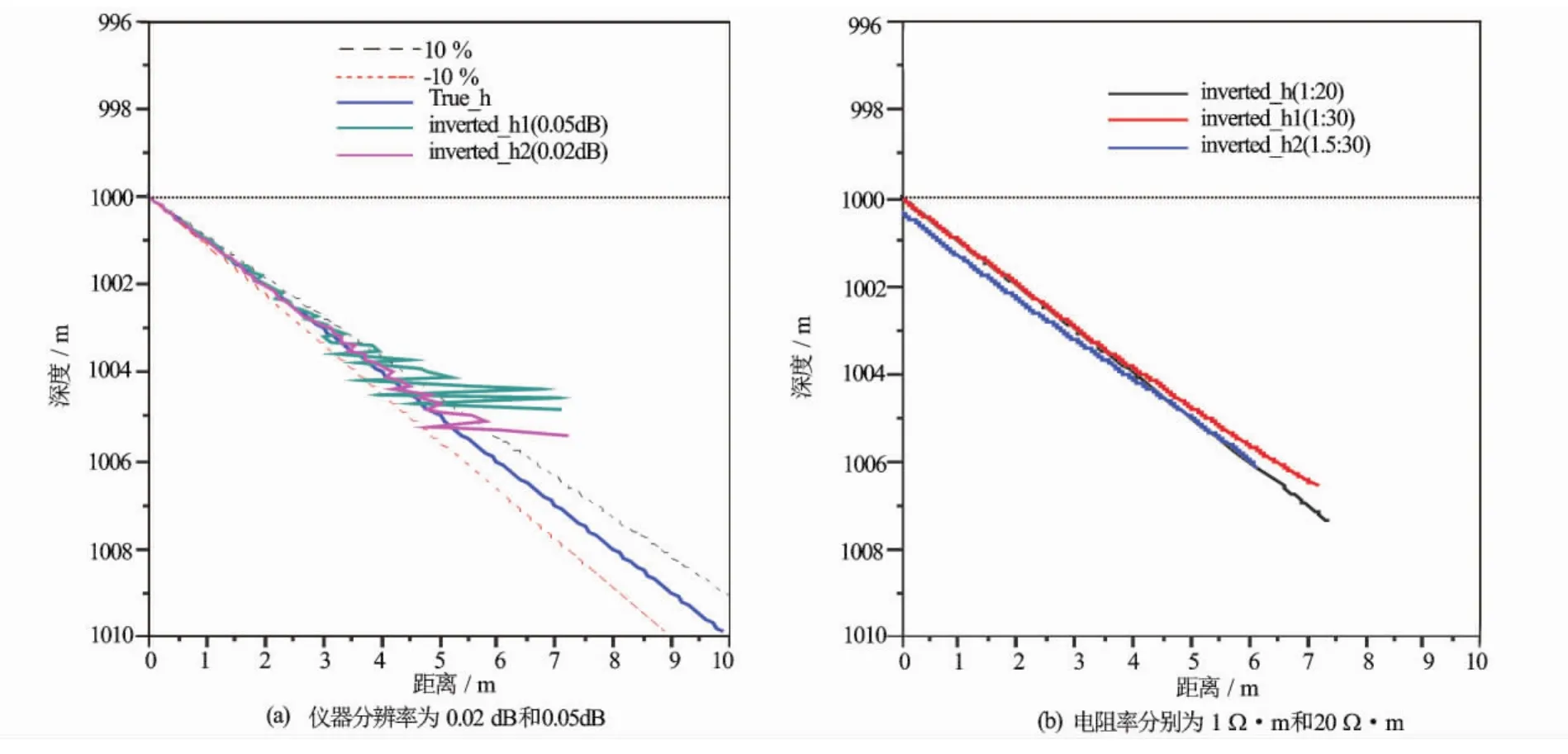
图10 不同情况下界面距离反演效果对比

6 结 论

（1）利用随钻方位电磁波仪器的界面响应特点可以预测和判断地层界面以及层界面的走向。随钻方位电磁波仪器的工作频率和线圈距会影响仪器的探测深度，相同信号灵敏度条件下，线圈距越大，工作频率越低，仪器探测深度越大。

（2）仪器探测深度除了与本身工作参数有关，还与仪器所处的地层有关。仪器所处地层的电阻率以及界面两侧电阻率对比度均会影响仪器的探测深度，地层电阻率越大，界面两侧电阻率对比度越大，仪器探测深度也越大，在不同地层模型情况下，哈里伯顿公司仪器ADR的界面探测深度可由2m增大到8m左右。

（3）界面距离反演过程中，在其他约束条件不变的情况下，界面两侧高电阻率地层的电阻率不准确对距离反演结果影响不大，尤其是越靠近界面的情况下；而低电阻率地层的电阻率值不准确则会造成反演界面距离出现比较大的误差，反演时采用的低电阻率地层电阻率值比真实值偏大，则反演得到的界面距离会偏小，因此界面距离反演过程中，相对低电阻率地层的电阻率值要尽量准确。

［1］ 周云凤，程为彬，陈世琳.随钻测量中工具面角的模拟解算 ［J］.中国测试，2010，36（3）：15－18.

［2］ David Kennedy W，Bill Corley，Stephen Painchaud，et al.Geosteering Using Deep Resistivity Image from Azimuthal and Multiple Propagation Resistivity ［C］∥SPWLA 50th Annual Logging Symposium，Paper ZZ，2009.

［3］ Qiming Li，Dzevat Omeragic，Lawrence Chou，et al.New Directional Electromagnetic Tool for Proactive Geosteering and Accurate Formation Evaluation While Drilling［C］∥ SPWLA 46th Annual Logging Symposium，Paper UU，2005.

［4］ Douglas Seifert，Saudi Aramco，Roland Chemali，et al.The Link Between Resistivity Contrast and Successful Geosteering ［C］∥ SPWLA 52nd Annual Logging Symposium，Paper VVV，2011.

［5］ 梁灿彬，秦光戎，梁竹健.电磁学 ［M］.北京：高等教育出版社，1985.

［6］ 肖加奇，张庚骥.水平井和斜度井中的感应测井响应计算 ［J］.地球物理学报，1995，38（3）：396－404.

［7］ 杨锦舟，魏宝君，林楠.倾斜线圈随钻电磁波电阻率测量仪器基本原理及其在地质导向中的应用 ［J］.中国石油大学学报：自然科学版，2009，33（1）：44－49.

［8］ 魏宝君，田坤，张旭，等.定向电磁波传播随钻测量基本理论及其在地层界面预测中的应用 ［J］.地球物理学报，2010，53（10）：2507－2515.

［9］ 陈华，范宜仁，邓少贵，等.水平井中随钻电阻率实时确定地层界面方法 ［J］.吉林大学学报：地球科学版，2011，41（5）：100－106.

［10］ 洪有密.测井原理与综合解释 ［M］.2004：128－137.

［11］ 杨震，岳步江，刘庆成.大斜度井随钻电磁波层厚影响模拟及机理分析 ［C］∥第六届中俄测井国际学术交流会论文集，2010：93－98.

［12］ Michael Rabinovich，Fei Le，Jeremy Lofts，et al.Deep？How Deep and What？The Vagaries and Myths of“Look Around”Deep－resistivity Measurements While Drilling［C］∥ SPWLA 52nd Annual Logging Symposium，Paper NNN，2011.

［13］ Omeragic D，Li Q，Chou L，et al.Deep Directional Electromagnetic Measurement for Optimal Placement［C］∥SPE97045，2005.