基于三轴地震波传感器的舰船被动定位方法

李 响，白正勤，刘旭东

（海军蚌埠士官学校兵器系，安徽 蚌埠233012）

0 引言

在浅海环境中，航行舰船的辐射噪声由于浅海低频截止效应，低频段的辐射噪声和海底介质相互耦合产生沿海底传播的舰船地震波场，而其中起主要作用的舰船低频噪声场是由舰船内部或外部的动力干扰引起的舰船结构振动向外辐射噪声所引起的［1］。舰船地震波场含有丰富的舰船目标信息，从而成为探测舰船目标并实施定位的一种有效方式［2－4］，在水中兵器中有重要的应用价值。由于保密原因，国外对该领域的深入研究鲜有报道，而国内仍处于起步阶段，局限于舰船地震波场传播特性的理论研究，尚未涉足舰船地震波场的应用研究。因此，本文提出了利用置于海底的动圈式三轴传感器接收舰船地震波信号，并对舰船目标进行被动探测定位的方法。

1 传感器设计

从舰船地震波信号的特点以及系统功耗这两个主要方面着手，选择适合水底环境使用的舰船地震波场传感器。

1.1 传感器的选择

舰船地震波信号主要是舰船辐射噪声耦合到海底所产生的沿着海底界面传播的表面波，属于低频微弱振动，具有一般地震波的特点。因此，可以借鉴海底结构勘探常用的地震检波器（压电式和动圈式），并加以改进。相对于压电式检波器，动圈式检波器有较低的输出阻抗、较好的信噪比和较低的使用频率，可测量微小的振动，有一定的抗横向振动能力。同时，其后继信号处理电路简单，并且传感器本身不需要电源供电。因此，选用进行舰船地震波场信号接收。

1.2 传感器结构特点

动圈式检波器结构如图1所示，其机电转换通过线圈相对磁铁往复运动实现。线圈及线枢由一个弹簧系统支撑在永久磁铁的磁极间隙内，组成一个振动系统。当线圈在磁极间隙中运动时线圈切割磁力线，同时在线圈两端产生感应电势，感应电势的大小与线圈切割磁通量的速度成正比，即与其相对于磁铁的运动速度成正比，所以，动圈式检波器也称为速度检波器［5－6］。以垂直检波器为例：在接收到垂向运动时，磁铁随之运动，但线圈由于其惯性而趋于保持固定，使线圈和磁场之间有相对运动，输出感应电势。而对于水平的运动，线圈相对于磁铁是不动的，则它的输出为零。

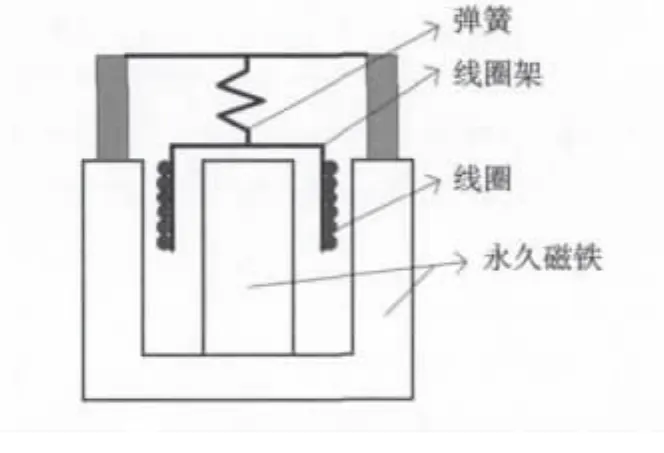
图1 动圈式检波器结构示意图Fig.1 Thestructure feature of moving－coil seismometer

1.3 传感器方向特性

由于自身结构特点，动圈式检波器具有天然的“8字形”方向性，沿传感器轴向的输出灵敏度最大，假设最大灵敏度为I0，则偏离传感器轴β角方向的有效灵敏度为I1＝I0cosβ，如图2所示。利用此方向特性可以确定振动波相对于传感器轴的偏角，即波达方向。为了更好地利用舰船地震波场，只接收单一分量的信号是不够的。由3个相同参数的动圈式检波器两两正交组成三轴地震波传感器（一个垂直方向，两个水平方向）。则，三轴地震波传感器在三个方向各有“8字形”的方向性。

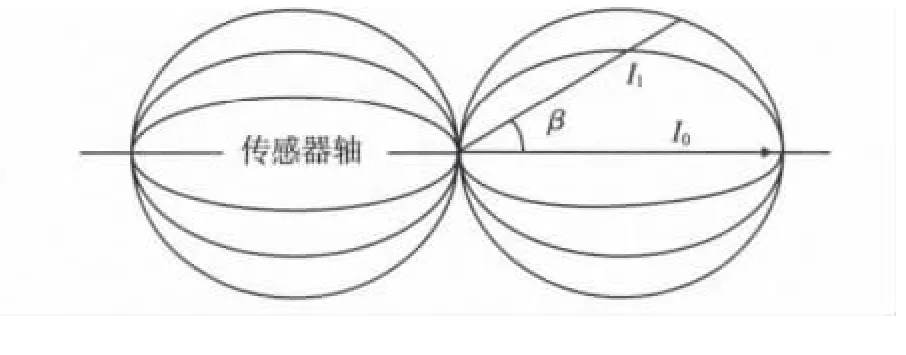
图2 “8字形”的方向性Fig.2 The directivity of single sensor

2 基于传感器的被动定位算法

2.1 三轴传感器输出特性

三轴传感器布放于海底，接收航行舰船的空间振动信息，输出包含目标方位信息的三分量信号：vx，vy，vz，如图3所示。

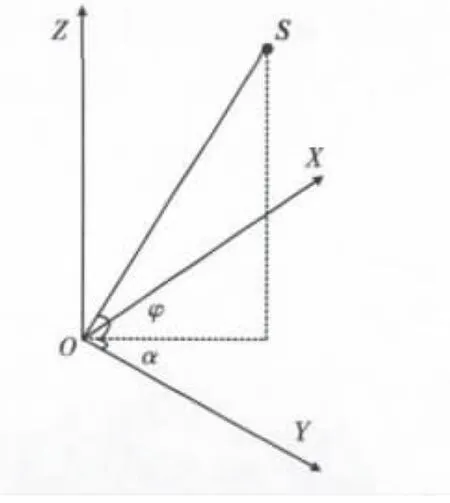
图3 信号波达方向Fig.3 The direction of arrival

声源发出的声波入射到三轴传感器上，其三轴输出分量为：

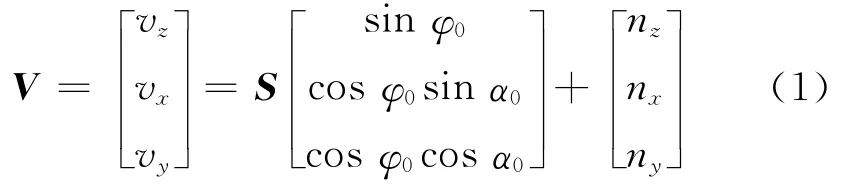
式（1）中，S是入射声波；φ0是目标俯仰角；α0是目标方位角；nz是Z轴输出的噪声，nx是X 轴输出的噪声，ny是Y轴输出的噪声，假设噪声为零均值、高斯白噪声，互不相关，且与声源互不相关。

2.2 被动定位算法

假设在各向同性的均匀噪声场中，对三轴传感器的输出信号V＝ ［vz（t）vx（t）vy（t）］T，分别以U ＝ ［sinφ cosφsinα cosφcosα］T作为权重进行加权求和：

加权求和信号Y的平均功率为：

式（3）表明，当且仅当φ＝φ0，α＝α0时，P（φ，α）达到最大，此时：

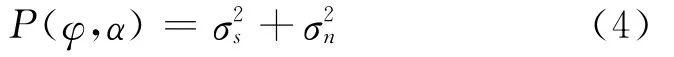
即P（φ，α）对声波入射方向的响应最大，且φ＝φ0，α＝α0。因此，可以通过空间峰值搜索的方法确定目标的俯仰角和方位角［7－8］。

2.3 仿真计算

针对2.1节的被动定位算法进行仿真计算，仿真信号为单频信号，模拟目标相对于传感器的俯仰角为10°，方位角为20°的舰船噪声信号。图4为信噪比为0 dB时进行定位计算的结果，计算所得的俯仰角为11°，方位角为20°。结果表明：定位算法对仿真信号能够准确的定位，而且定位算法和信号频率无关。

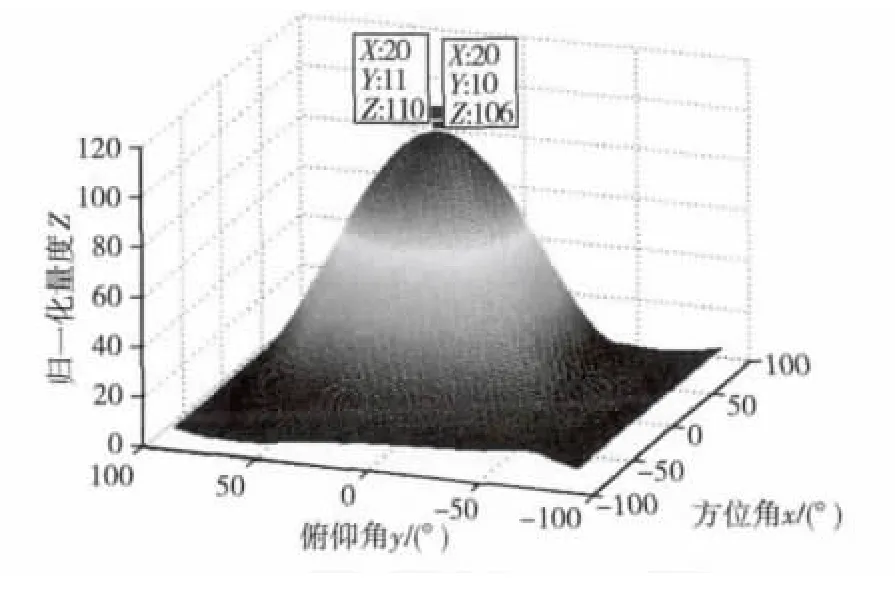
图4 入射信号的仿真计算（10°，20°）Fig.4 DOA estimation result versus elevation

3 实验分析

为了检验传感器的实际接收效果，以及定位算法对实际舰船目标的探测定位能力，在自然水域进行了信号接收和定位试验。

检测装置由密封舱、三轴地震波传感器、信号调理和数据采集存储电路组成，并将其置于水底，实验情况如图5所示。为了解决检测装置布放时传感器姿态的不确定性，将三轴地震波传感器安装在万向架上，使三轴传感器在任何姿态下都能实现水平调节，保证传感器的正常工作。

图6为湖试环境下三轴地震波传感器实测的2km外气枪声源信号，三分量信号清晰可辨（水深16m，气枪置于水下1.5m，气枪压力6MPa，检测系统置于淤泥质湖底）。试验表明：三轴地震波传感器可以很好地接收到水中声源的噪声信号。

图7为海上实船试验三轴传感器实测的舰船信号（试验区域水深20m，检测系统置于淤泥质海底）。试验表明：接收到三分量信号具有明显的区域特性，可明确的识别出舰船的通过特性曲线。

图8为由算法估计出的俯仰角随时间的变化曲线和目标通过特性曲线的对比图（实线为计算所得估计曲线，虚线为实测通过曲线）。由图可得，利用定位算法估计的目标俯仰角变化曲线和实际的目标通过特性曲线符合较好，表明该算法可有效地判别出目标相对于检测装置的位置及通过区域。

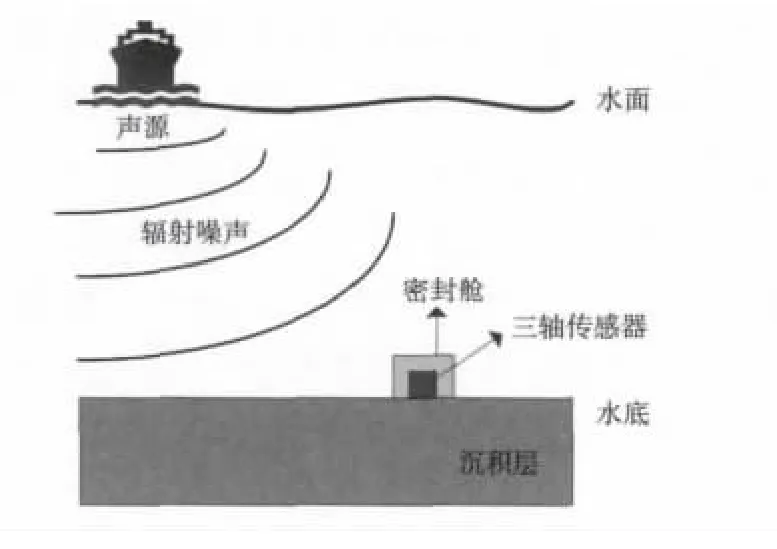
图5 实验示意图Fig.5 The diagrammatic sketch of the lake test

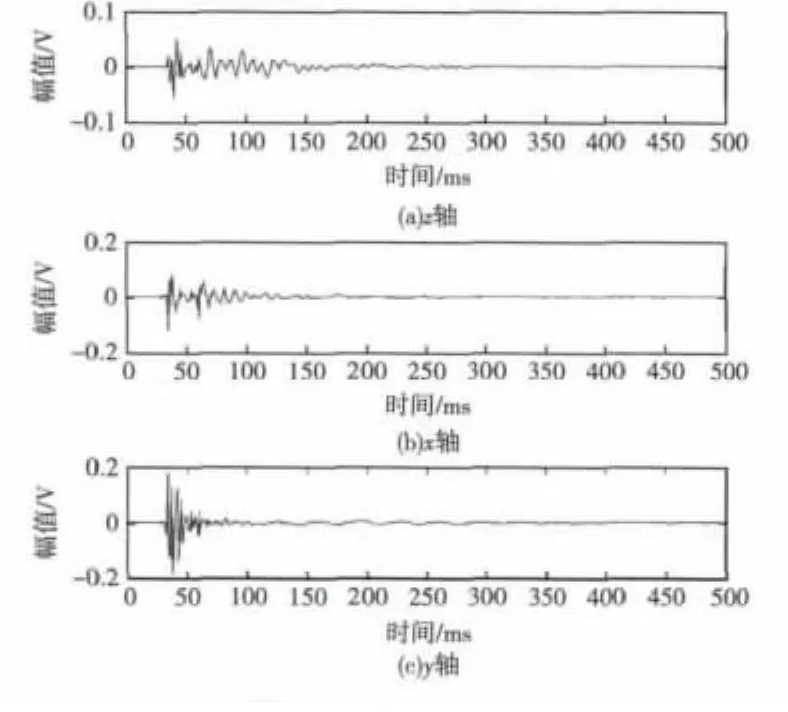
图6 实测气枪声源信号Fig.6 The air gun signal

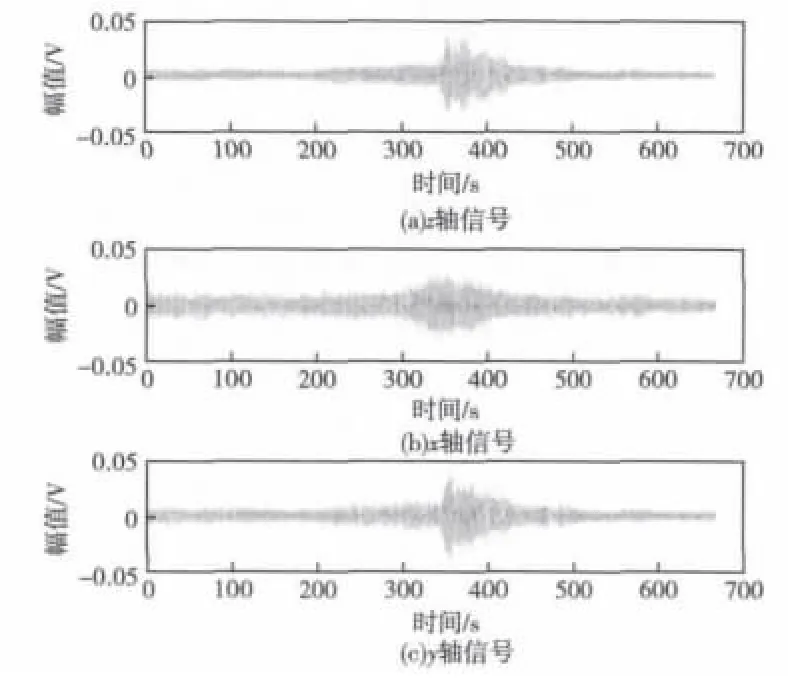
图7 实测舰船信号Fig.7 The ship signal

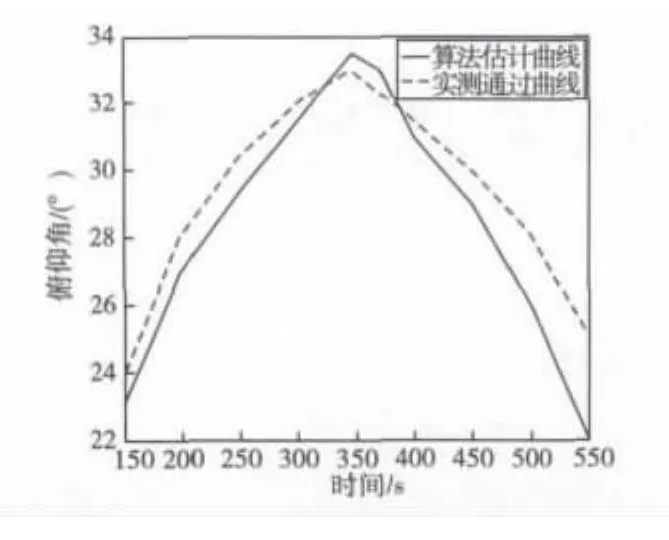
图8 俯仰角变化曲线Fig.8 The variational curve of elevation

4 结论

本文提出了利用动圈式三轴传感器对舰船目标进行探测定位的方法。该方法通过动圈式三轴传感器检测舰船地震波信号，利用其自身的结构特点和方向特性，结合算法对舰船目标进行定位。试验表明，置于海底的动圈式三轴传感器能够很好地接收舰船地震波信息，输出含有目标方位特征的三分量信号，结合算法实现了对目标的被动探测定位，对水下目标探测具有重要的意义。但是，本文限于单传感器对单目标的探测定位，而对于多传感器、多目标的探测定位还有待于进一步的研究。

［1］陆鑫森，金咸定，刘涌康.船体振动学［M］.北京：国防工业出版社，1980.

［2］Kuperman W A.Bottom Interacting Ocean Acoustic［M］.NATO：Marine Sciences，1980.

［3］Schmalfeldt B.Ambient and ship－induced low frequency noise in shallow water，Bottom－interacting ocean acoustics［R］.La Spezia，Italy：SACLANT ASW Research Center，1989.

［4］Ali H B，Schmalfeldt B.Seismic Sensing of Low－Frequency Radiated Ship Noise［R］.La Spezia，Italy：SACLANT ASW Research Center，1984.

［5］朱蕴璞，孔德仁，王芳.传感器原理及应用［M］.北京：国防工业出版社，2005.

［6］周征.传感器原理及检测技术［M］.北京：清华大学出版社，2007.

［7］王永良.空间谱估计理论与算法［M］.北京：清华大学出版社，2004.

［8］孙超，李斌.加权子空间拟合算法理论与应用［M］.西安：西北工业大学出版社，1994.