基于稀疏表示的水声信号分类识别

廖明熙，张小蓟，张 歆

（西北工业大学航海学院，陕西 西安 710072）

0 引言

一直以来，水下目标识别与分类算法是水下舰船噪声信号处理研究的重点及难点，其主要方法是通过舰船的发动机噪声来判断舰船的类别。在水下目标识别特征提取方法的研究中，有众多的特征提取方法［1］：功率谱分析理论［2］、小波及小波包理论［3］、HHT 变 换 方 法、MFCC 方法。其 中 基 于HHT变换具有比较好的特征识别效果［4－5］。

这些特征提取与分类识别算法都是使用原信号，受限于水声系统的带宽，必须先将数据保存在水声设备中，然后将信号传输到地面站进行处理，给实际应用带来不便。因此如何降低数据量，并进行实时处理成为水声信号特征提取及分类识别的新方向。2006年Candès等提出了压缩感知（Compressed Sensing，简称CS）理论［6－7］，该理论的本质内容是稀疏或可压缩信号的少量随机的线性投影即包含了重构和处理的足够信息，也就是仅仅利用信号稀疏或可压缩的先验和少量的全局线性测量可以获得精确的信号重建，该理论被美国科技评论评为2007年度十大科技进展。而一般的语音信号在DCT基下是可稀疏的［8－9］，满足压缩感知理论要求，能够实现精确重构。因此信号的稀疏表示必然包括信号的所有特征信息，因此使用稀疏表示作为信号特征在理论上可行，并且能够减轻数据处理任务。

本文提出将CS理论中稀疏表示作为舰船噪声信号的特征向量，然后使用支持向量机（SVM：Support Vector Machine）分类方法进行分类识别，仿真结果表明该方法与传统特征提取方法相比，不仅速度得到了大幅度的提高，而且有效提高了识别率。

1 压缩感知理论

压缩感知理论指出，如果一个信号是稀疏的，或者在某个变换域内是稀疏的，那么就可以使用一个与变换基不相关的观测矩阵将稀疏的高维信号“压缩”成低维信号，并且如果稀疏满足一定的条件，还可以通过“压缩”之后的低维信号恢复成原信号［10－11］。

设空间R存在长度为N的列向量x∈R，且信号中是K稀疏的，即信号中只有K个系数不为零或明显大于其他系数，且满足K≤N。用矩阵表示：

y称之为x的感知值，长度为M（M＜N）的列向量，称之为测量自然数，Φ为M×N的测量矩阵。

但是在实际当中，这样稀疏的信号并不常见，经过研究发现，如果一个信号在某种正交变换下是稀疏的，那它同样也适用于压缩感知理论，用矩阵表示：

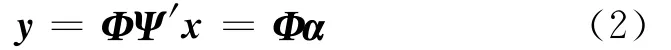
其中Ψ′表示正交基变换（N×N），α为稀疏系数，即信号x经过正交变换之后是稀疏的。经过大量的实验研究，得到一个更广泛的结论，即如果一个信号在过完备字典下是稀疏的，则该信号同样满足压缩感知理论，用矩阵表示：

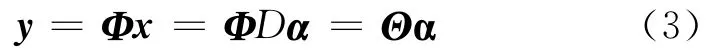
D为冗余字典，α称之为信号x在字典D下的稀疏表示。这个结论将使得非常多的信号都适用于压缩感知理论。

2 基于稀疏表示的水声分类识别

2.1 DCT字典设计

大多数的信号本身是不稀疏的，而语音信号在离散余弦DCT（discrete cosine transform）域上有着近似稀疏性［8］，DCT有很强的能量聚焦作用，舰船噪声的高频分量很小，根据实验，发现舰船噪声在DCT基下近似稀疏，将DCT系数取绝对值并排序得到系数分布，如图1所示。

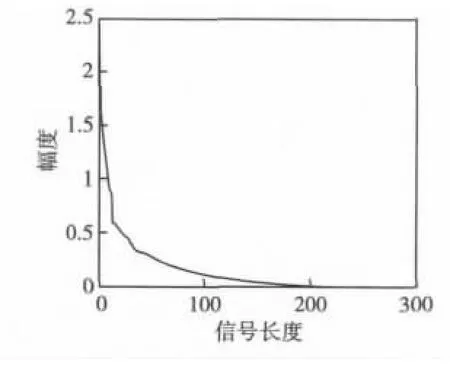
图1 水声信号DCT系数分布Fig.1 The signal DCT coefficient distribution

从图1可以看出，水声信号在DCT字典下是近似稀疏的。对于数字序列信号x（n），n＝0，1，…，N－1，其DCT变换如式（4）：

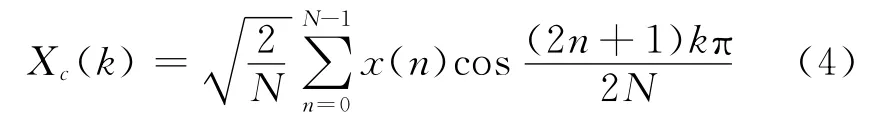
其中DN是大小为N×N的DCT变换矩阵，也就是DCT字典。

2.2 K－SVD算法

水声信号在DCT字典下是近似稀疏的，为了能够在DCT字典下严格稀疏，需要对DCT字典进行稀疏训练。这里使用 K－SVD 算法［8－9］。K－SVD 算法模型：

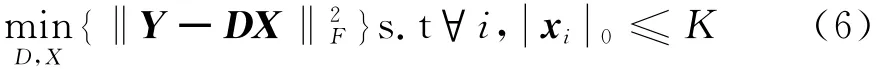
化简得：

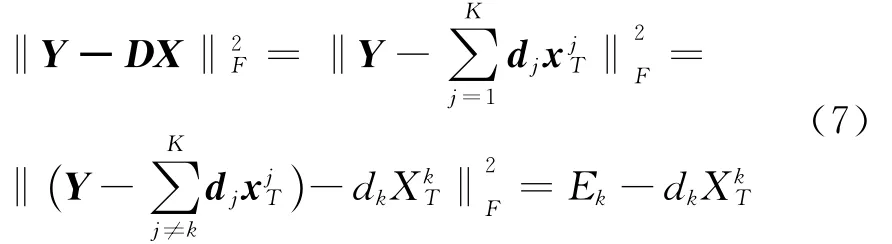
其中，Y＝ ｛yi｜i∈ ［1 ，M ］，yi∈Rn｝为需要进行稀疏表示的信号集，X＝｛xi｝为稀疏系数，K为稀疏度。得到稀疏化之后的字典D。K－SVD使用算法求解稀疏字典具体计算步骤如下：

1）字典为DCT字典。在信号集中随机选取M个信号样本组成初始信号集Y；

2）固定D，求解X，这是一个SR的实现过程，在K－SVD算法中，使用OMP算法实现；

3）根据已经求得的X，求解D，对Ek使用SVD分解，求解dk，依次更新D中所有的列。

4）循环步骤2），步骤3），重复迭代，得到稀疏化之后的冗余字典D。

2.3 信号的稀疏表示求解

根据以上算法得到稀疏化之后的冗余DCT字典，从而可以通过计算得到舰船噪声信号在DCT冗余字典下进行的稀疏表示。即求解式（5）中的α：

由于信号长度是N，字典尺寸为M×N，M＜N，因此该算法是个NP－hard问题，常用的求解算法有基追踪（BP）［12］、匹配追踪法（MP）［13］和正交匹配追踪法（OMP）［14］。结合 OMP的速度优势，这里采用OMP算法，求解问题如式（9）所示：

其中D＝ ｛di｜i＝1，2，…，M ｝，是已知的字典，X＝ ［x1，x2，…，xN］是待求解系数信号，OMP算法［14］是针对基于最小化l0范数问题而提出来的。

OMP算法步骤如下：

1）初始化残差r0＝y，索引集Λ0为空集，t＝1。

2）找出信号残差rt和字典列dj内积中最大值所对应的下标λ，即：

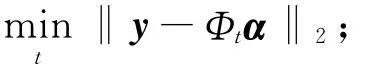
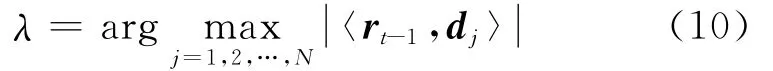
3）更新索引集Λt＝Λt∪｛λt｝，记录找到的字典中的重建原子集合：

5）更新信号残差

6）t＝t＋1，判断是否满足t＞K，若满足，则停止迭代，否则循环步骤二到步骤五。得到的Λ即为所求字典D，而α为所求稀疏表示系数。

3 仿真实验

3.1 K－SVD实验

经过仿真实验发现，稀疏字典的计算时间tdic与测量次数M成正比，如图2所示。

从K－SVD计算算法当中不难看出M的增长计算的复杂度是近似线性增长的。

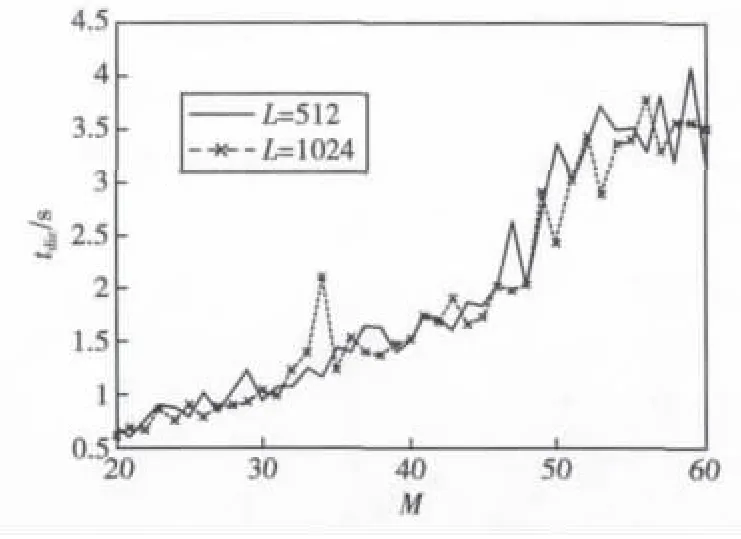
图2 测量次数M对tdic的影响Fig.2 The impact on tdicof measurements M

3.2 分类实验

从压缩感知理论体系中可知，如果一个信号在某个变换域是稀疏的，则信号的稀疏表示必然包含了原信号的大部分信息。所以不同类型的舰船噪声信号的稀疏表示必然不一样，因此可以将稀疏表示直接作为特征向量进行分类。根据稀疏表示中的K个非0系数这个特点，非常适合使用SVM分类器进行分类。具体步骤如下：

1）生成样本集：三类实际舰船噪声信号A、B、C。按长度 N 组成样本集：XA、XB、XC。

2）设计DCT冗余字典：初始化DCT字典，尺寸为M×N，初始化的训练信号集为A、B、C三类样本集中任选M个样本数。由于本文着重分类，不对信号进行重构，因此稀疏度K可任选，然后使用K－SVD算法进行训练得到稀疏化的DCT冗余字典D。

3）求解稀疏系数：使用OMP算法对XA、XB、XC三类样本集中每个样本求解系数，得到系数集αA、αB、αC。

4）特征提取：对XA、XB、XC三类样本中除去M个用于训练字典的样本，然后进行特征提取。使用文献［4］中提到的方法，提取信号的EMD频谱峰值，组成特征样本集TA、TB、TC。

5）训练分类模型：在XA、XB、XC与αA、αB、αC各类样本集中，随机抽取P个样本构成训练集，进行SVM训练，得到分类模型。

6）分类识别：在剩下的XA、XB、XC以及αA、αB、αC各样本集中进行分类识别。

对比实验结果，取M ＝40、64，N ＝1024，P＝20，K取4～20；5），6）重复100次，实验结果如图3所示。

由图可知，随着稀疏度K值的减小，平均识别率在增加，其原因在于特征数据越稀疏，对于SVM分类器的分类效果越好。当足够稀疏时，识别率超过了使用EMD频谱峰值作为特征的识别率。其中，当K＝4，M＝64，N＝1024的时候，各识别率如表1所示。

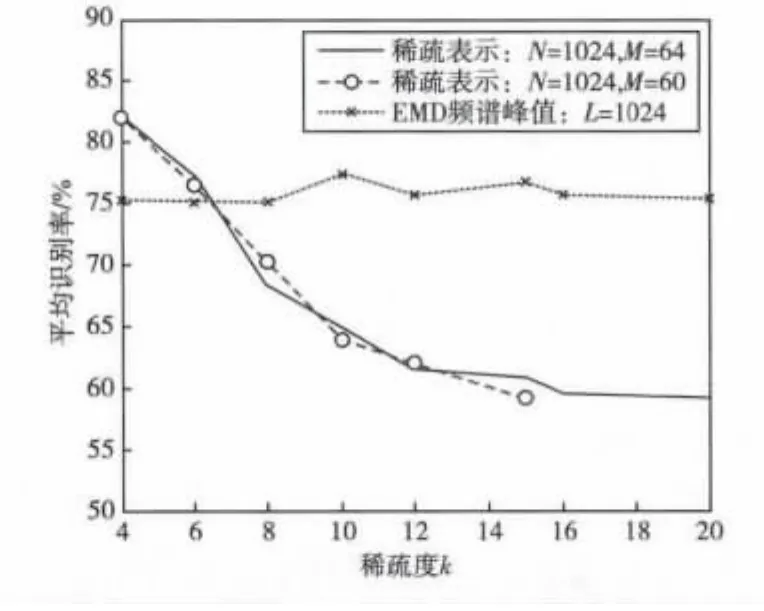
图3 在不同特征下平均识别率比较Fig.3 Comparison of recognition rate in different feature

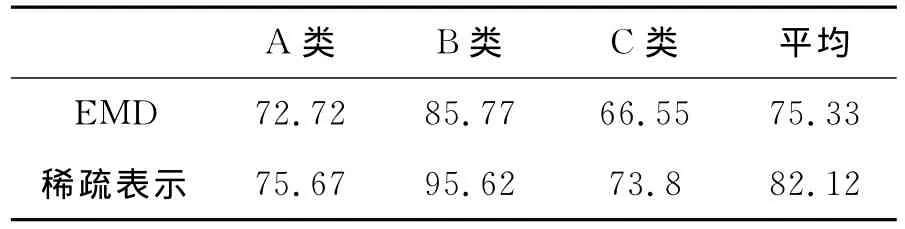
表1 分类识别率比较Tab.1 Comparison of classification rate

由表1可知，使用稀疏表示作为舰船噪声信号分类作为特征，识别率较好于EMD特征提取方法。

3.3 特征提取及分类时间性能比较

使用EMD频谱峰值作为特征进行分类识别所需要的总时间t1，包括特征提取所需要的时间temd加上分类需要的时间tsvm1。如式（13）所示：

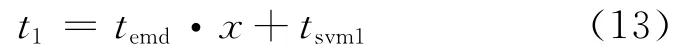
使用稀疏表示作为特征进行分类识别所需要的总时间t1，包括稀疏字典求解时间tdic、特征提取所需要的时间tspr以及分类需要的时间tsvm2。由于本算法中使用了三类信号，如式（14）所示：

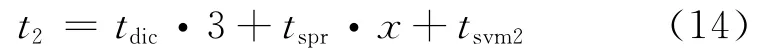
其中公式（8）（9）中的x表示样本数个数，“3”表示三类信号需要各计算一个字典。经过多次仿真实验，在t1中，temd·x达到了t1的99% 以上。在t2中，当x足够小的时候，tdic·3远大于其他两项，随着x的增大，占的比重越来越小。由于tsvm1、tsvm2相对于其他几项可以忽略，因此在实验中未计入t1、t2。针对x对t1与t2之间影响仿真结果如图4所示。

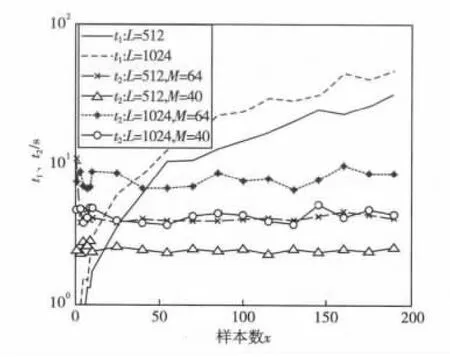
图4 信号长度与特征提取耗时倍数的关系Fig.4 The relationship between signal length and multiple consuming

由图可知，使用稀疏表示作为特征的计算所用总时间增长斜率Δt1要远远小于使用EMD频谱峰值作为特征的计算所使用总时间增长斜率Δt2。经过仿真计算得到计算EMD频谱峰值所需要的时间是计算稀疏表示的时间的20倍。如式（15）所示：

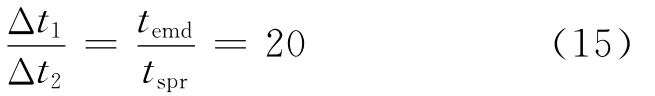
从以上仿真实验中，可以得出结论：使用稀疏表示作为信号特征可以大大缩短使用EMD频谱峰值作为特征的计算时间。

4 结论

本文提出了一种新型的水声信号特征表征方法，即采用压缩感知中的稀疏表示作为舰船噪声的特征，以实现用小量的特征信号取代大量的原始数据信号。具体实现中采用K－SVD算法训练得到DCT冗余字典，在某种程度上包含了原信息的主要特征，并使用OMP算法对实际信号样本进行求解稀疏系数。本文通过使用SVM分类算法对使用稀疏表示的目标特征集进行分类识别，实现了大幅提高目标识别速度的目的，在水声信号分类中有非常重要的实际意义，实验仿真结果表明，在选取合适的参数时，使用本文所提出的方法在分类识别率性能上优于目前性能较好的特征分类器，具有非常高的实用价值。

［1］李新欣.船舶及鲸类声信号特征提取和分类识别研究［D］.哈尔滨：哈尔滨工程大学，2012.

［2］史广智，胡均川.基于小波包和1（1／2）维谱的舰船辐射噪声频域特征提取及融合［J］.声学技术，2004，23（1）：4－7.

［3］樊养余，陶宝祺.舰船噪声的1（1／2）维谱特征提取［J］.声学学报，2002，27（1）：71－76.

［4］刘深 ，张小蓟，牛奕龙，等.基于IMF能量谱的水声信号特征提取与分类研究 ［J］.计算机工程与应用，2014（3）：203－206.

［5］张小蓟，张歆，孙进才.基于经验模态分解的目标特征提取与选择［J］.西北工业大学学报，2006，24（4）：453－456.

［6］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：1289－1306.

［7］DONOHO D.Compressed sensing［J］.IEEE Trans.Information Theory，2006，52（4）：1289－1306.

［8］孙林慧.语音压缩感知关键技术研究［D］.南京：南京邮电大学，2012.

［9］戴琼海，付长军，季向阳.压缩感知研究［J］.计算机学报，2011，34（3）：425－434.

［10］Candès E J.Compressive sampling［C］／／Proceedings on the International Congress of Mathematicians.Madrid：IEEE，2006：1433－1452.

［11］Candès E J，Romberg J，Tao T.Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information［J］.Information Theory，IEEE Transactions on，2006，52（2）：489－509.

［12］Chen S S，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit［J］.SIAM journal on scientific computing，1998，20（1）：33－61.

［13］Needell D，Vershynin R.Greedy signal recovery and uncertainty principles［C］／／Electronic Imaging 2008.International Society for Optics and Photonics.2008，68140J－68140J－12.

［14］Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.Information Theory，IEEE Transactions on，2007，53（12）：4655－4666.