水声通信中单载波频域均衡器设计方法

姚智文，张 歆

（西北工业大学航海学院，陕西 西安710072）

0 引言

水声信道是一个带宽受限的、时变的复杂无线信道，其多径时延扩展引起的码间干扰（ISI），是实现高速率水声通信的主要障碍。因此，有效抵抗ISI的技术一直是水声通信研究的热点［1－2］。近年来，带有频域均衡的单载波调制（SC－FDE）技术受到人们的重新关注［3－7］。由于具有良好的抗ISI性能以及低复杂度，SC－FDE在水声通信领域中也得到了研究。

SC－FDE要在水声通信中得到有效应用，需要对均衡器的结构和参数估计进行深入的研究。SCFDE有线性与非线性两种结构。文献［5］在水声通信中采用了线性结构的频域均衡，并用海试数据进行了验证，但是均衡效果欠佳。文献［3］中提出了一种无线电应用中的非线性结构频域均衡——迭代块判决反馈均衡（IB－DFE），并按照最小均方误差准则设计了前馈和反馈滤波器系数的迭代修正算法，但文中缺乏对频域信道的有效估计。文献［8］则对计算均衡器参数所需的信道估计进行了研究，提出的联合迭代均衡和信道估计（JECE）算法，将基于训练和面向判决的信道估计算法有效地结合起来，并以均衡器反馈信号的可靠度为准则，选择最佳信道估计值，但文中未对不同结构的均衡效果进行比较。本文针对此问题，提出了水声通信中单载波频域均衡器设计方法。

1 SC－FDE的系统模型

1.1 SC－FDE的数据结构

在SC－FDE系统中，发射数据流经符号映射后被分为多个数据块，每个数据块用已知伪随机（PN）码进行扩展，以使发射信号满足可循环性。为了进行信道估计，在第一个数据块前加训练块，训练块由训练序列和PN扩展序列组成，数据结构如图1所示。本文采用具有常数包络和均匀谱特性的Chu序列作为训练块，长度取为E，用长度为F的PN码扩展为长度N＝E＋F的训练块。设信道的最大多径时延为L，则取E＞L，F＞L。接收端利用训练序列进行频域信道估计，其估计结果用于均衡器参数的计算。

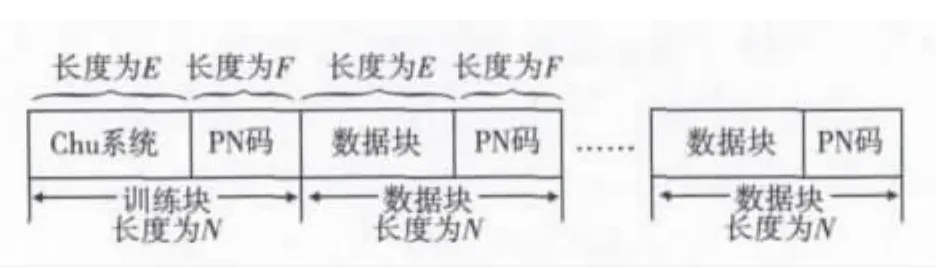
图1 SC－FDE的数据结构Fig.1 Data Structure of SC－FDE

在SC－FDE系统中，发射端发送的时域信号，在接收端经离散傅里叶变换（DFT）到频域后，经过频域均衡抵消掉ISI后再回到时域中进行检测判决。其中频域均衡（FDE）可采用线性结构和非线性结构，下面就频域均衡的两种不同结构进行探讨。

1.2 线性结构的频域均衡

采用线性结构频域均衡的接收端原理框图如图2所示。时域接收信号rn首先进行串并转换和DFT后得到频域信号Rk，然后通过频域均衡得到信号Uk，均衡信号Uk再经过IDFT和并串转换后得到时域信号un，经检测判决后输出发送信号的估计。

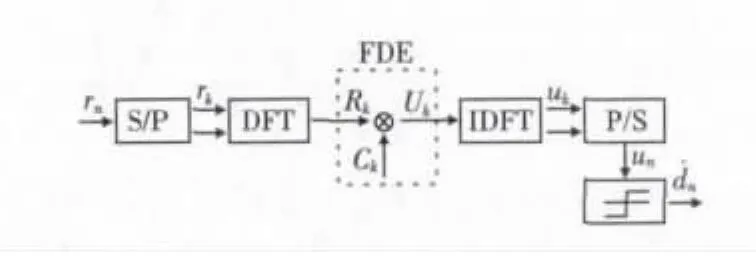
图2 采用线性结构的频域均衡接收端框图Fig.2 Block diagram of FDE receiving end adopting a linear structural

设时域接收信号为：

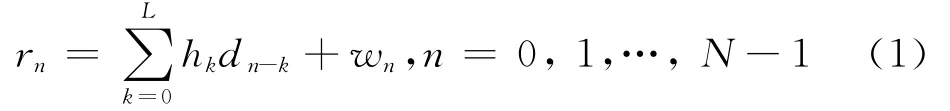
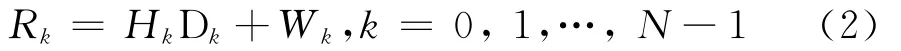
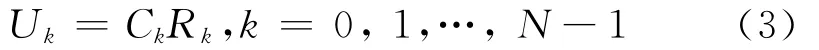
式中Ck为滤波器系数。按照线性最小均方误差（MMSE）准则可得［3］

其中Mw为噪声功率，MDk为频域信号功率。

1.3 非线性结构的频域均衡

采用IB－DFE结构的频域均衡接收端如图3所示。时域接收信号经过DFT后得到频域输入信号Rk，经前馈滤波器后得到频域信号Xk，该信号与反馈滤波器输出信号Yk相减，抵消ISI，得到频域均衡输出信号Uk，再经过IDFT、并串转换和检测判决得到。其中反馈滤波器的输入信号是由判决信号加上PN码扩展之后，再经过串并转换和DFT得到的频域信号。在IB－DFE中，由于滤波器系数的迭代计算需要利用前一次均衡的判决信息，所以采用IB－DFE结构的均衡器为非线性频域均衡器。

图3 采用IB－DFE结构的频域均衡接收端框图Fig.3 Block diagram of FDE receiving end adopting IB－DFE structural

设第l次迭代时，前馈滤波器输出为：

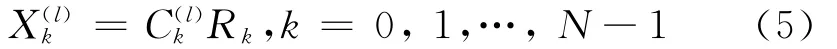
反馈滤波器输出为：

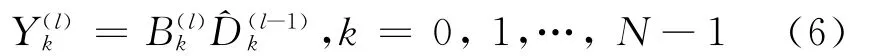
则均衡器输出为：

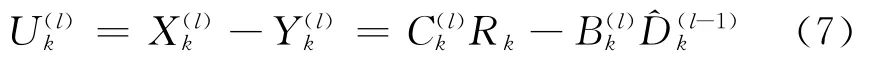
式中，C（l）k、B（l）k分别为第l次迭代时前馈和反馈滤波器的系数，其中前馈滤波器系数为［7］：

其中，k＝0，1，…，N－1。此时Ck（l）的计算不仅用到了噪声功率、信号功率以及信道估计参数，还包括发射信号与上一次迭代判决信号的相关函数

反馈滤波器系数为：

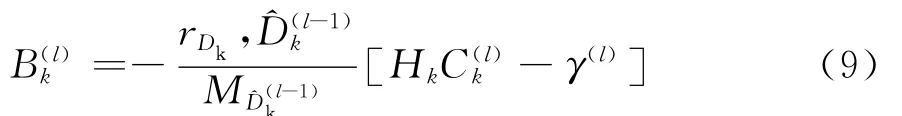
式中，γ（l）表示经过前馈滤波器后的信号幅度，表示为：

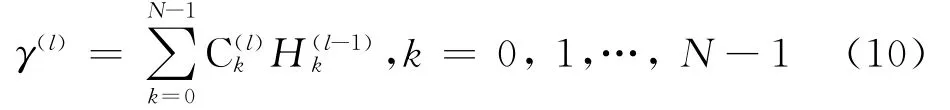
2 JECE算法原理

由式（4）、式（8）及式（9）中可以看到，信道系数Hk是计算频域均衡器参数的关键，因此，需要进行有效的信道估计。针对有多径时延和多普勒频移的水声信道，文献［8］中提出了一种联合迭代均衡与信道估计（JECE）算法。接收的训练序列转换到频域后，进行最小方差（LS）估计，形成基于训练的信道频域估计，用于IB－DFE的初次迭代；然后用均衡器输出的判决信号作为新的训练序列，形成面向判决的信道估计，再采用文献［9］中的方法将其与TS，k进行加权组合得到新的信道估计值，即

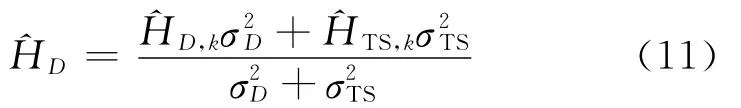
式中，σ2D和σ2TS分别是和TS，k的方差。

最后以均衡器反馈信号的可靠度ρ（l）（发射信号与上一次迭代判决信号之间的归一化相关系数的期望值）作为判决门限，选择第l次迭代时的信道估计与之间的最佳值作为信道估计Hk，形成联合迭代均衡与信道估计（JECE）算法，用于IB－DFE的前馈及反馈滤波器系数的计算。

本文主要借鉴文献［8］中提出的JECE算法进行信道估计。

3 仿真分析

我们用水声信道模型对SC－FDE的性能进行仿真，传输距离10km、水深200m和传输距离3km、水深50m的水声信道模型的参数如表1所示。表中的数据分别用最先到达路径的参数归一化，仿真数据为二进制随机数据，调制方式为QPSK，噪声为加性高斯白噪声，且假设接收时间同步完好。

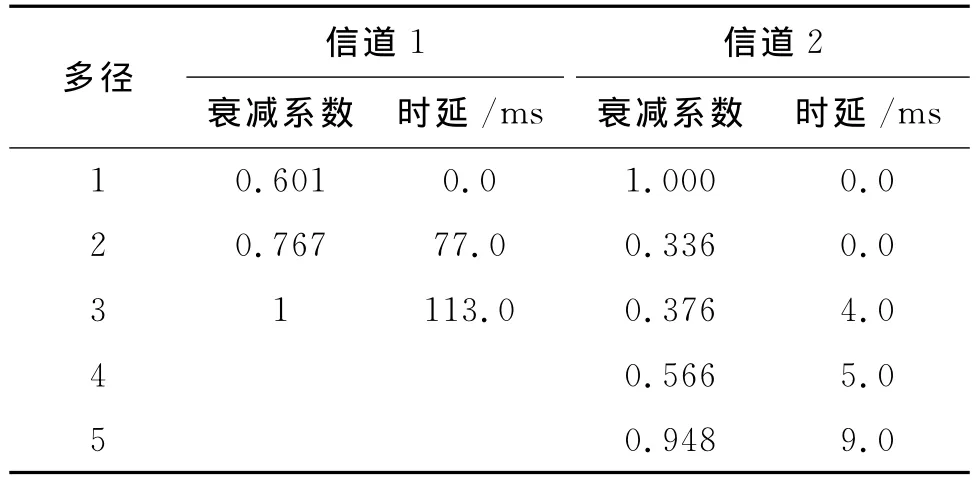
表1 水声信道模型的参数Tab.1Parameters of underwater acoustic channel model

3.1 非线性与线性均衡器的性能比较

图4为信道1中假设信道已知和采用信道估计（JECE）算法的IB－DFE与线性均衡器的误比特率（BER）曲线。仿真时，信号频率为5kHz，符号速率为500bps，相应的信道长度为L＝57。取数据块长度N＝1024，PN码长度F＝128。图中分别给出了IB－DFE（迭代4次，包含反馈信息）和线性均衡（迭代1次，无反馈信息）的BER曲线。仿真的数据数为5.98×104。由图可见，在信道1中信道估计条件下，同样在SNR＝16dB时，IB－DFE的BER曲线接近10－4，线性均衡器的BER还不到10－2；而在信道已知条件下，IB－DFE的BER曲线下降较快，在SNR＝12dB时就已达到10－4，线性均衡器BER则刚刚达到10－2。

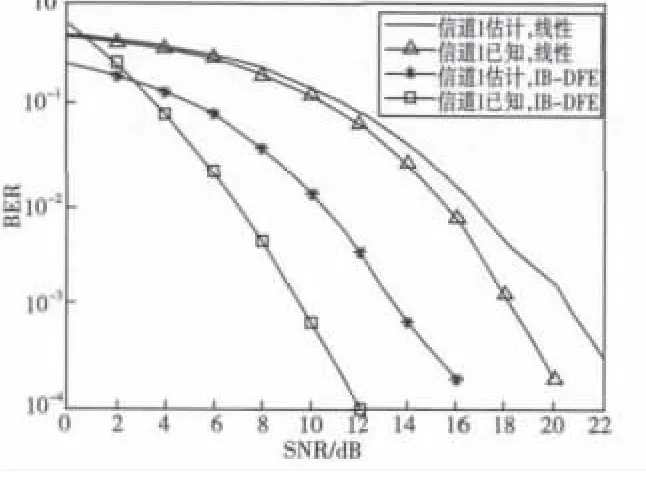
图4 信道1中均衡器的性能对比Fig.4 Performance comparison of equalizer in Channel 1

图5为采用信道2中的参数，在假设信道已知和信道估计条件下IB－DFE与线性均衡器的BER性能比较。仿真时，信号频率为5kHz，符号速率为1.25kbps，相应的信道长度为L＝11。取数据块长度N＝1024，PN码长度F＝32。由图可见，当SNR＝9.2dB时，采用信道估计的IB－DFE的BER曲线达到了10－3，此时线性均衡刚刚达到10－1；而在信道已知条件下，IB－DFE的BER曲线仅在SNR＝5.7dB时已经达到10－3，而线性均衡器的BER才刚刚达到10－2。虽然信道2中多径数目多，且发送符号速率较大，但是由于信道长度相比较信道1中的短，所以曲线收敛效果较好。

图5 信道2中均衡器的性能对比Fig.5 Performance comparison of equalizer in Channel 2

3.2 不同符号速率时IB－DFE的参数设计

图6是在信道2中，对于不同符号速率时不同结构均衡器的BER曲线。仿真时，信号频率为10kHz，当符号速率取1kbps时，相应的信道长度为L＝9。取数据块长度N＝256，PN码长度F＝16；当符号速率取2kbps时，相应的信道长度为L＝18。取数据块长度N＝512，PN码长度F＝32；当符号速率取5kbps时，相应的信道长度为L＝45。取数据块长度N＝1024，PN码长度F＝128。仿真的数据数为6.87×104。

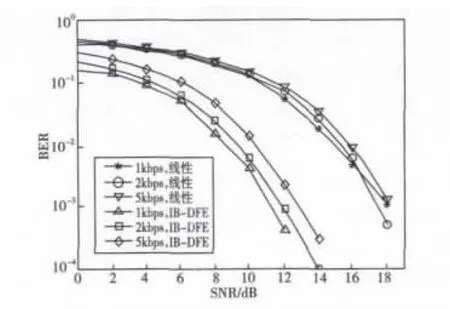
图6 不同符号速率时均衡器的BER曲线Fig.6 The BER curves of equalizer in Different symbol rates

由图6可见，在不同的符号速率1kbps、2kbps及5kbps情形下，分别根据相应的信道长度选取合适的数据块与PN码长度，有效抵抗多径效应，得到较好的误比特率性能。如图6所示，当符号速率为1kbps，SNR＝11.1dB时，IB－DFE的BER曲线达到了10－3，此时线性均衡刚刚达到10－1；当符号速率取为2kbps时，IB－DFE的 BER曲线在SNR＝12dB时达到10－3，而线性均衡器刚刚达到10－1。当符号速率取5kbps时，IB－DFE的BER达到10－3需要信噪比12.7dB，线性均衡器需要信噪比18.2dB。这说明可适当提高符号速率，利用IB－DFE同样可以得到较好的误比特率。

3.3 数据块长度对均衡器的性能影响

图7是在信道1中采用不同数据块长度的IB－FDE与线性均衡器BER曲线。仿真时，符号速率为200bps，信号频率为4kHz，相应的信道长度L＝23，选取F＝32，数据总数为5.6×104。

图7 不同数据块长度对均衡器的性能影响Fig.7 The performance impact on the equalizer of different data block lengths

由图可见，数据块长度对均衡器的性能有着较大的影响。当取数据块长度N＝256时，线性均衡器收敛效果很差，IB－DFE收敛效果也一般；当取N＝512时，IB－DFE收敛效果有所改进，在SNR＝12dB时，达到10－3，而线性均衡器还没有达到10－2；当取N＝1024时，IB－DFE的BER曲线收敛效果要明显优于线性，在SNR＝10.1dB时达到10－3，在12dB时达到10－4，而线性均衡器在SNR＝12dB时才刚刚达到10－1；当取N＝2048时，曲线收敛效果反而较差，这说明可适当增大数据块长度，有效降低误比特率，但同时也不是越大越好，这主要取决于发送的符号速率和信道参数。

3.4 均衡器的复杂度计算

按照文献［8］，不同均衡方案的计算复杂度可以用均衡过程中进行信号处理和滤波器设计所需的复数乘（CMUL）的次数来评估。在信号处理方面，N点DFT需要（N／2）log2N－N次CMUL。在IB－DFE中，接收端要经过1次DFT将时域信号转换到频域；同时在每次迭代时，前馈和反馈滤波器需要2 N次CMUL和2次（I）DFT，除了最后一次迭代仅需1次IDFT。因此每输出一个符号需要2 NI［（N／2）log2N－N＋N］／E－N／E次CMUL，其中，NI为迭代次数。表2中给出了在图7仿真条件下中N＝512时的IB－DFE与线性均衡器进行信号处理的计算复杂度。其中，线性均衡所需的CMUL为2［（N／2）log2N－N］／E＋N／E（迭代一次）。

表3为图7中当N＝512时不同结构中滤波器设计所需要的CMUL次数。对于IB－DFE来说，前馈和反馈滤波器的设计需要计算一次｜H｜2k，同时每次迭代又需要计算一次除和两次乘，即所需的CMUL为（3 NI＋1）N。然而对于线性结构来说，计算复杂度为N。

由表2可见，无论是线性结构均衡器还是IB－DFE，用于信号处理的计算复杂度都与数据块长度有关，线性结构所需的CMUL次数要少于IB－DFE（NI＝4）。由表3可见，在4次迭代的情况下，IB－DFE的计算复杂度远远大于线性结构均衡器，这是由于在IB－DFE中需要迭代计算滤波器的系数，但是这种迭代的设计不涉及矩阵运算，只涉及DFT和矢量的乘、除，因而实现过程较为简单，对数字信号处理（DSP）和现场可编程门阵列（FPGA）等实现平台的要求也会大大地降低。

表2 信号处理的计算复杂度Tab.2 The computational complexity of signal processing

表3 滤波器设计的计算复杂度Tab.3 The computational complexity of filter design

4 结论

本文提出了水声通信中单载波频域均衡器设计方法，该方法联合了基于训练与面向判决信道频域估计，并以均衡器反馈信号的可靠度作为判决门限，选择最佳信道估计值，用于均衡器的前馈及反馈滤波器系数的计算。仿真表明，采用非线性结构的单载波频域均衡相比线性结构均衡器具有更好的误比特率性能，对存在严重ISI的水声信道具有更好的适应性及可实现性。

［1］Singer A C，NeLon J K，Kozat S S.Signal proces－sing for underwater acoustic communications ［J］.IEEE Communications Mag，2009，47（1）：90－96.

［2］郭瑜晖，孙海信，程恩，等.水声系统单载波频域均衡方法比较［J］.厦门大学学报（自然科学版），2012，51（5）：849－853.

［3］Benvenuto N，Tomasin S.Iterative design and det－ection of a DFE in the frequency domain ［J］.IEEE Transactions Communications，2005，53（1）：1867－1875.

［4］Pancaldi F，Vitetta Giorgio M，Kalbasi R，et al.Singlecarrier frequency domain equalization ［J］.IEEESignal Processing Mag，2008，25（5）：37－56.

［5］Zhang J，Zheng Y R，Xiao C S.Frequency－domain equalization for single carrier MIMOunderwater acoustic communications［C］∥IEEE Conference OCEANS 2008，Quebec，Canada，2008：1－6.

［6］Zhang C，Wang Z C，Pan C Y，et al.Low－comple－xity iterative frequency domain decision feedback equalization［J］.IEEE Transactions Vehicular Tec－hnology，2011，60（3）：1295－1301.

［7］Miguel L，Rui D，Paulo M.SC－FDE for offset mo－dulations：an efficient transmission techniquefor broadband wireless systems［J］.IEEE Transactions Communications，2012，60（7）：1851－1861.

［8］张歆，张小蓟.水声信道中的迭代分组判决反馈均衡器［J］.电子与信息学报，2013，35（3）：683－688.

［9］Coelho F，Dinis R，Montezuma P.Joint detection and channel estimation for block transmissionsch－mes［C］∥Military Communications Conference 2010，San Jose，USA，2010：1765－1770.