基于线性混合盲分离的谐波检测和消除方法

向东阳，彭小宏，毕季明

（海军陆战学院，广东 广州 510430）

0 引言

在各种电信号、声信号的处理过程中，谐波干扰的检测和消除通常是必不可少的环节。谐波检测的方法有很多，比如谱分析方法、FFT、神经网络等［1］。谐波消除的常用方法是采用数字陷波滤波技术，但陷波滤波器毕竟有一定的带宽，因此对有用信号成分会造成一定的破坏。在众多的谐波消除方法中，实际上最有效方法应该是直接从混合信号中减除干扰成分，当然前提是能够直接获得参考信号。传统的自适应滤波方法就是基于这一思路而建立的，但是传统自适应滤波要求参考源信号中不能混有目标信号成分，否则滤波效果会受到很大影响。文献［2］提出了一种基于独立分量分析的谐波检测和消除方法。从统计信号处理的角度来看，谐波干扰和待检测的目标信号通常来自于两个相互独立的信号源。因此可以将谐波干扰消除问题转化为盲源分离问题，不过与一般的盲源分离问题相比较，我们对谐波干扰的先验知识（例如谐波频率和时域波形的基本形式）有一定的了解，因此比一般盲源分离问题的处理要简单。

文献［2－8］的谐波检测和消除模型虽然是基于独立分量分析的原理，但是有的没有考虑尺度和次序不确定性问题［2］，有的虽然考虑到了，但是没有给出有效的解决方法［4］，因此所估计出的谐波幅度和相位有可能是不准确的。本文针对此问题，提出了基于线性混合盲分离的谐波检测和消除方法。

1 线性混合盲分离模型

盲信号分离（Blind Signal Separation ，BSS）技术是指在具有多个信号源的复杂环境中，传感器测量到的信号是多个信号源的混合信号，从混合信号中将原始信号分离出来的问题。按照信号混合的方法一般分为线性瞬时混合、卷积混合和非线性混合三种。固定点算法［9］（Fast－ICA）是源信号线性瞬时混合盲分离方法中的一种，通常由对混合信号预处理和独立分量提取两部分组成，其中预处理包括信号的中心化和白化处理两部分。这里重写信号混合与分离的公式为：

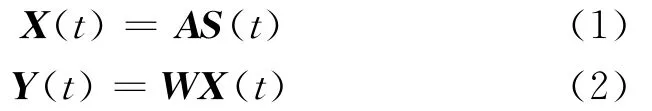
其中 S（t）＝ ［s1（t），s2（t），…，sn（t）］T为 源 信 号，X（t）＝ ［x1（t），x2（t），…，xm（t）］T（n ≤ m）为混合信 号，A 为 混 合 矩 阵，Y（t）＝ ［y1（t），y2（t），…，yn（t）］T为估计的源信号，W 为分离矩阵。

信号经过预处理后，在进行独立分量提取之前，必须寻找一种独立性的判据来度量分离信号的非高斯性，也即独立性。该独立性可用负熵来度量。对于一个随机变量y，若其概率密度为p（y），则负熵的定义式为：

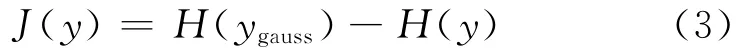
式（3）中，ygauss是具有和y相同方差的高斯度量；而H（y）＝－∫p（y）lgp（y）dy为随机变量y的信息熵。然而，实际计算时，由于随机变量y的概率密度p（y）未知，故一般用下式进行估计：

式（4）中，G（·）为某个非二次函数，其有多种选择，已证明下列形式是有用的［9］：

由式（4）可知，y的非高斯性越强，E｛G（ygauss）｝就越小，负熵J（y）越大，因此可以用负熵极大化来作为独立性的判据。即在做完混合信号的预处理后，依据负熵判据来寻找矩阵W，使得Y＝WX的负熵最大。也就是对E｛G（Y）｝＝E｛G（WX）｝求极值，使E｛G（WX）｝最大。根据牛顿迭代法求解，经过代数化简后得：

式（7）中，Wi（k＋1）是第k＋1次迭代时矩阵W 的第i行，g（·）为G（·）的导数，g＇（·）为g（·）的导数，‖·‖2代表求2－范数。

总之，采用负熵的固定点算法步骤可总结如下：

1）将混合信号X去均值，然后加以白化；

2）任 意 选 择 Wi的 初 值 Wi（0）， 要 求‖Wi（0）‖2＝1，i＝1，2，…，n；

3）根据（7）更新和归一化Wi；

4）设定阈值，根据ΔWi的大小判断算法是否收敛，如未收敛，继续步骤3）。

基于负熵的固定点算法的优点在于：由于采用牛顿法，收敛较有保证，可以证明它具有三阶的收敛速度；而且迭代过程中无需引入调节步长等人为设置的参数，因而更加简单方便。

2 基于线性混合盲分离的谐波检测和消除的原理

设x（t）是记录的混合信号，其中含有目标信号s0（t）和谐波信号p（t），即

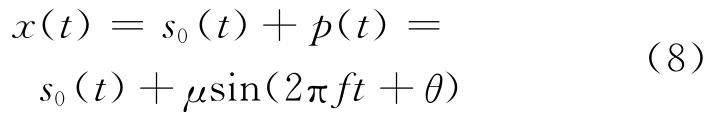
式（8）中，μ 为谐波幅度，θ为谐波相位，f 为谐波频率。

一般情况下，谐波的频率可以通过简单的谱分析获得，但谐波的幅度和相位通常是未知的。如果有同步测量的谐波干扰源信号，那么幅度和相位估计问题就相对比较简单。如果没有谐波参考源，则会比较复杂。此种情况下，通常采用从混合信号中提取一段不含目标信号或目标信号较弱的数据段进行谐波幅度和相位的估计，不过估计精度往往难以保证。盲信号处理技术为谐波幅度和相位估计提供了一个新的思路。文献［2］用线性盲分离方法进行了谐波频率和相位的估计，但是没有考虑独立分量分析的尺度和次序不确定性问题，因此其模型是不完整的，估计的谐波幅度和相位有可能是不正确的。本文在其基础上进行了改进，考虑了独立分量分析的尺度和次序不确定性因素，并推导了幅度和相位的求取方法。

文献［2］对式（8）进行了分解，得到

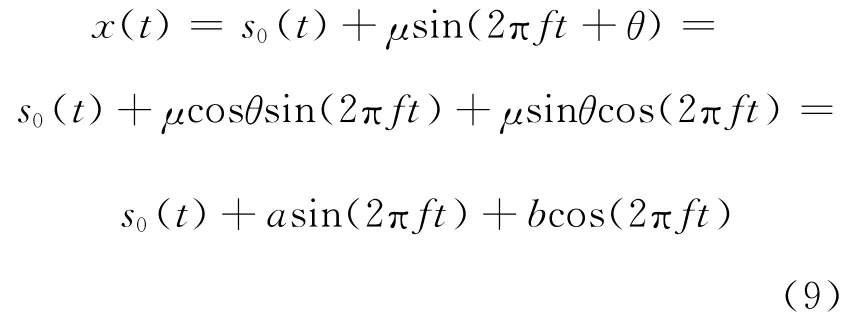
式（9）中，μ为谐波幅度，θ为谐波相位，f为谐波频率。重新构造两路参考信号为：s1（t）＝sin（2πft）和s2（t）＝cos（2πft）；则此时混合信号可记为：X（t）＝［x（t），s1（t），s2（t）］T，相应的混合过程用矩阵形式可表示为：

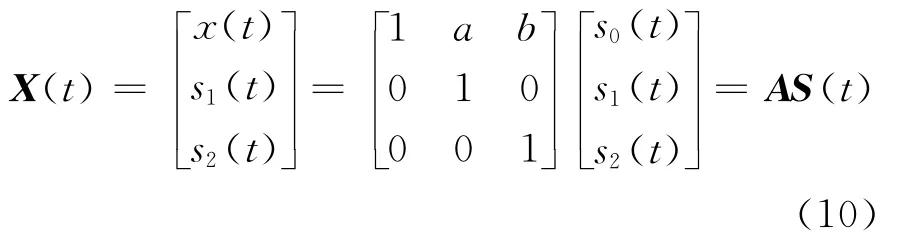
式 （10）中，A 为 混 合 矩 阵，S（t）＝［s0（t），s1（t），s2（t）］T为源信号。

采用固定点算法对三路混合信号X（t）＝［x（t），s1（t），s2（t）］T进行分离，估计的混合矩阵记为，估计的源信号记为（t），则有：

由于盲分离方法分离出的信号与源信号存在尺度和排列次序的不确定性，则有：

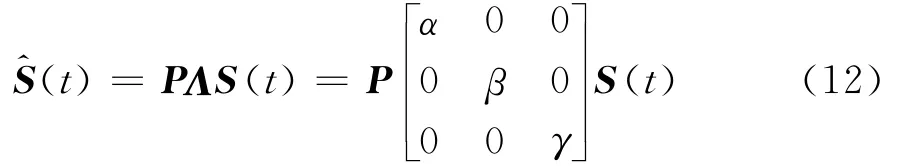
式（11）中，Λ为任一非奇异的对角矩阵，P为任一置换（或排列）矩阵，其任意一列或一行只有一个为1的非零元素，则（11）可写为：

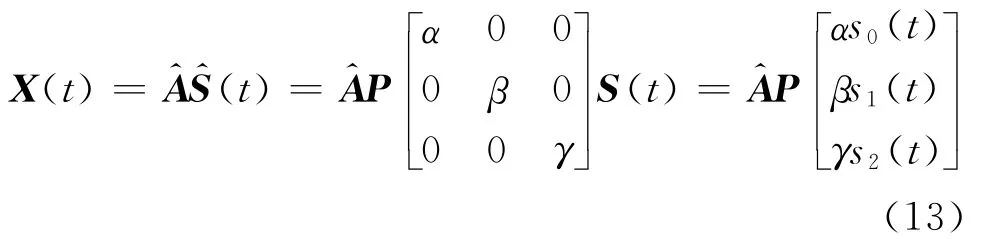
进一步将（10）写为：

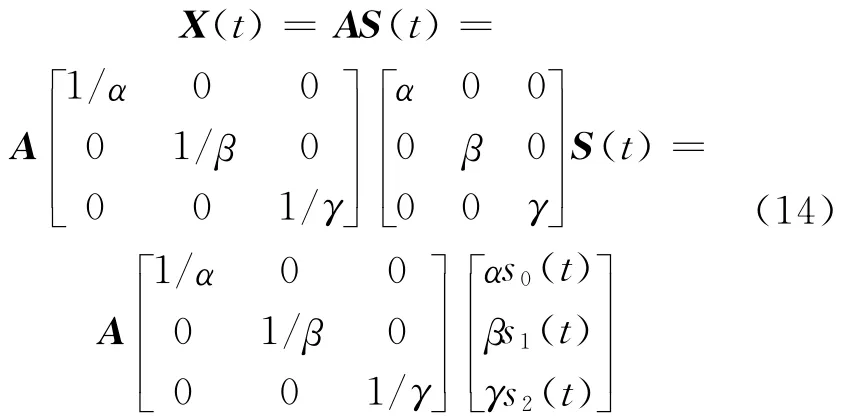
对比式（13）与式（14）可以发现，

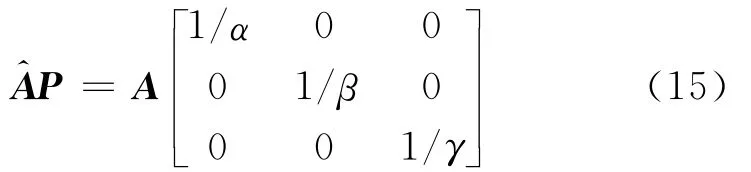
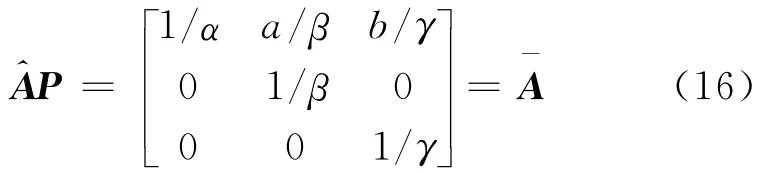
根据式（16），因为P为置换矩阵，则盲分离方法估计出的混合矩阵与右边的矩阵只是存在列排列上的差异。因此矩阵除了第一行外，其它行都应该只有一个元素不为零，并且这些行的不为零元素均不属于同一列。实际计算中由于误差的存在，混合矩阵中的那些应该为零的元素不可能准确的等于零，但是肯定接近于零，并且远小于同一行中最大的元素（绝对值）。只要将矩阵的列按照矩阵的结构进行重新调整，再根据矩阵相等则对应元素相等的原则，就可以将参数a，b，α，β，γ计算出来，进而由和θ＝arctan（b／a）得到谐波p（t）幅度和相位。与此同时，在调整的列的顺序时将分离信号的顺序也做相应调整，即如果估计的混合矩阵的第i列和第j列互换，则估计的源信号t）的第i行和第j行也互换，调整完毕后，将）的第一行除以α，即可得到消除谐波信号后的目标信号s0（t）。

综上所述，如果混合信号为x（t），对于单个谐波信号p（t）的检测和消除，改进的基于线性盲分离模型的谐波检测和消除方法可归结为图1所示，算法整体流程。

图1 算法整体流程框图Fig.1 Flow chart of the algorithm

3 仿真分析

为了检验本文提出的方法对谐波参数进行检测的准确性，分别对单个和多个谐波信号参数的检测采用Matlab7.1进行了仿真，计算机CPU为Intel Celeron 2.6G，内存为2G。

3.1 单个谐波信号的幅度、相位检测及其消除

采用Matlab生成如下的混合信号：

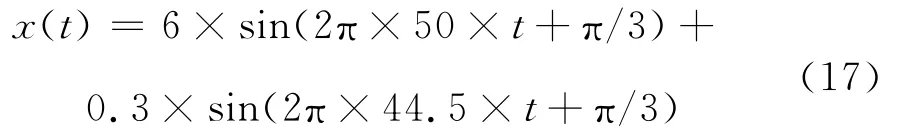
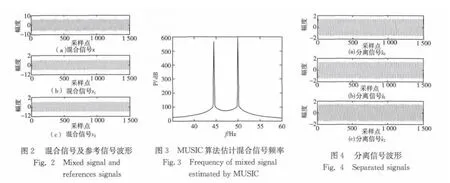
采样频率为1Hz，采样时间为1.5s，波形如图2所示，采用MUSIC算法估计信号频率为50Hz和44.5Hz（如图3），但是不能估计其幅度和相位，若要检测44.5Hz信号的幅度和相位，根据第3节的分析，则一路源信号为：

再构造两路参考信号：

则源信号应为S（t）＝ ［s0（t），s1（t），s2（t）］T，混合信号为：

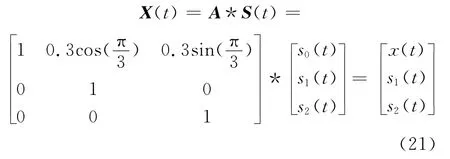
式中A为混合矩阵。

采用固定点算法对X（t）进行分离，耗时0.06 s，分离信号的波形如图4，得到估计的混合矩阵为：

理想情况下分离信号与源信号的幅度和排列次序应该一致，但从矩阵、图2和图4中可看出，分离信号和源信号s0、s1、s2的幅度和排列次序明显不一致。若直接根据矩阵和分离信号求源信号幅度和相位，肯定会出现误差，因此必须对进行调整。将（22）式的列按照（16）式中矩阵的结构重新排序，可得到为：

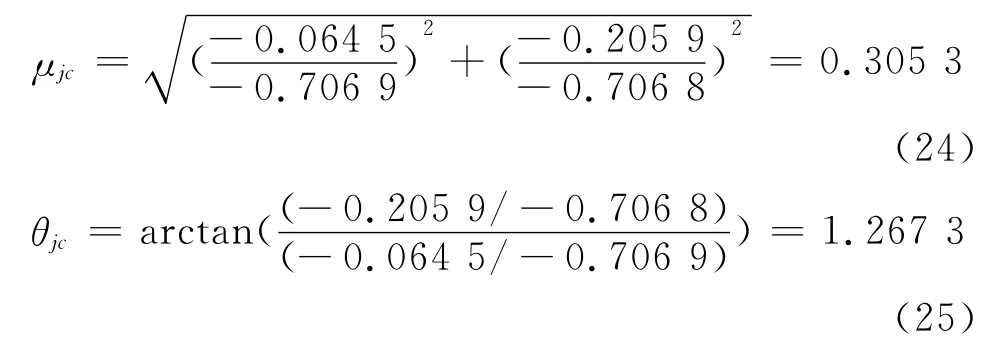
将检测结果和真实值进行对比，结果见表1，相对误差的计算方法为：

表1 谐波检测误差Tab.1 The error of harmonic detection

由表中可以看出，幅度的检测比较准确，但是相位的检测误差较大，如何提高其精度还需进一步研究。

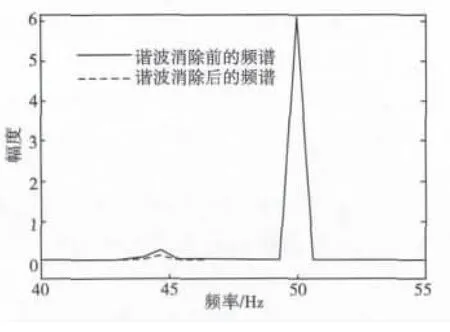
图5 混合信号及其消除谐波后的频谱Fig.5 Frequency of mixed signal before and after harmonic removal

3.2 多个谐波信号的幅度检测

盲分离方法进行谐波相位检测时误差较大，下面仅进行多个谐波信号的幅度检测，其方法和单个谐波信号幅度检测的不同之处在于需要根据检测的谐波个数构造多个参考信号，其他过程相同。

采用Matlab生成如下的混合信号：

采样频率取为1kHz，采样时间为1.5s，波形如图6所示，采用MUSIC算法估计信号频率为45.7Hz、44.5Hz和46.9Hz（如图7）。为了检测频率为44.5Hz和46.9Hz信号的幅度，构造四路参考信号：

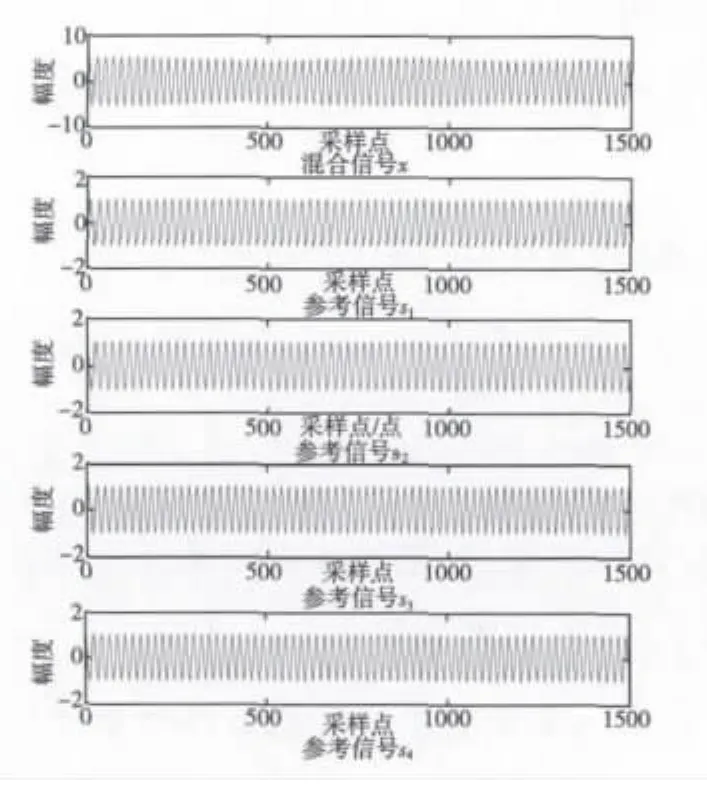
图6 混合信号及参考信号波形Fig.6 Mixed signal and references signals

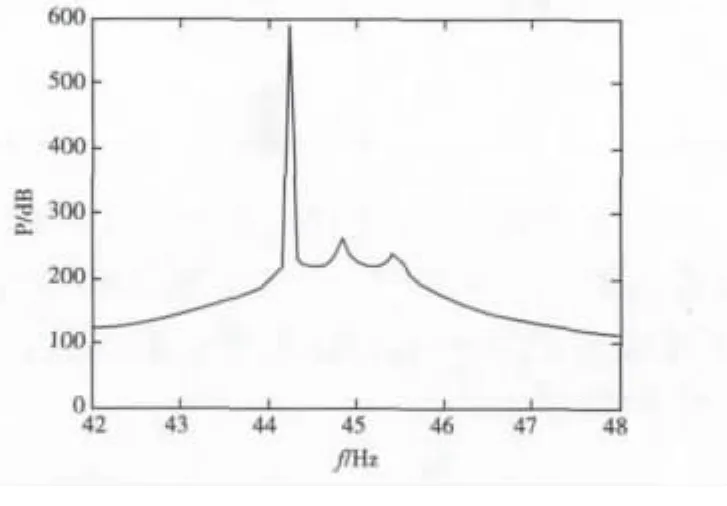
图7 MUSIC算法估计混合信号频率Fig.7 Frequency of mixed signal estimated by MUSIC

得到混合信号向量X（t）＝ ［x（t），s1（t），s2（t），s3（t），s4（t）］T，采用固定点算法对 X（t）进行分离，耗时0.06 s，得到估计的混合矩阵为：

频率为44.5Hz信号的幅度为：

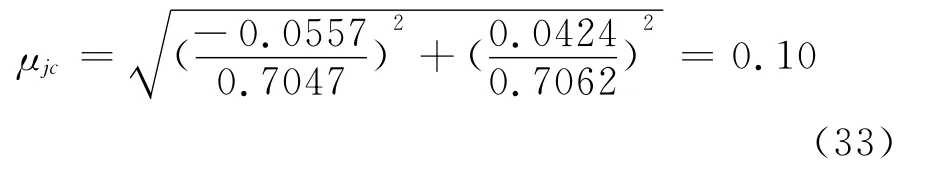
频率为46.9Hz信号的幅度为：

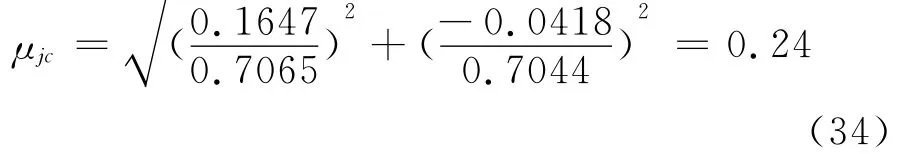
利用FFT方法求出了x（t）中44.5Hz和46.9 Hz的信号的幅度，并将其和利用本文方法求出的幅度进行了对比，结果见表2。

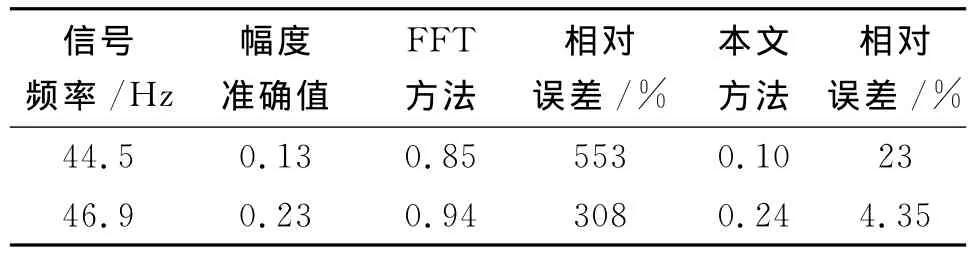
表2 不同方法求取幅度的结果比较Tab.2 comparison of magnitude for different methods

由表中可看出，在采样时间为1.5s时，由于发生频谱泄漏，利用FFT求解间谐波幅度是不准确的，而本文方法求出的幅度虽然也有误差，但其精度远好于FFT方法。

4 结论

本文提出了基于线性混合盲分离的谐波检测和消除方法。该方法在传统基于独立分量分析的谐波检测和消除方法的基础上，采用矩阵方法分析了线性混合盲分离模型中分离信号与源信号的对应关系，得到了一种消除分离信号尺度和次序不确定性的方法，使传统的线性盲分离模型应用于谐波检测时得到的谐波参数更加准确，仿真实例证明了该方法在谐波幅度检测和谐波消除方面的正确性和有效性，但应用在谐波相位检测时误差较大，还需作进一步深入研究。同时，本文的方法还可以应用于故障诊断中故障信号的准确分离、提取以及检测。

［1］向东阳，王公宝.基于FFT和神经网络的非整数次谐波检测方法［J］.中国电机工程学报，2005，25（9）：35－39.

［2］吴小培，李晓辉，孔敏.基于独立分量分析的谐波估计和消除［J］.电工技术学报，2003，18（4）：56－60.

［3］甘武，孙云连.基于独立分量分析的工频通信中的谐波干扰消除［J］.继电器，2005，33（10）：17－20.

［4］季宇，孙云莲，李晶.基于独立分量分析的谐波检测［J］.电力系统保护与控制，2009，37（8）：14－18.

［5］金贵斌，王曙钊，金桂梅，等.基于独立分量分析的同频、邻频及谐波干扰消除法［J］.电测与仪表，2009，46（6）：1－4.

［6］郑东方，陈红坤，杨志平.独立分量分析在谐波源辨识中的应用［J］.电力系统及其自动化学报，2012，24（4）：139－144.

［7］汪斌，王年，蒋云志.基于动态独立分量分析算法的谐波检测［J］.电力系统保护与控制，2011，39（2）：40－44.

［8］王继，王年，汪炼.基于改进Fast－ICA的电能质量谐波检测［J］.电力系统保护与控制，2010，38（18）：126－130.

［9］杨福生，洪波.独立分量分析的原理与应用［M］.北京：清华大学出版社，2006.