基于过零数衰减的震动探测预警分析方法

陈 卓，方 向，张卫平，王怀玺，胡尚夫

（1.解放军理工大学野战工程学院，江苏 南京210007；2.武汉军械士官学校，湖北 武汉430075）

0 引言

远距离的目标预警可有效提高对目标定位、跟踪及快速打击的反应速度。常用的预警技术有震动探测预警技术和声探测预警技术，两者都是采用被动式探测，隐蔽性好，作用距离远。震动探测预警技术因其具有更好的抗干扰性而被普遍用于各种地面探测系统中［1－4］。目前国内外对预警效果的评价是通过预警率来衡量的，一般是指通过对探测得到的目标震动信号进行过零分析来判断目标是否出现，并进行多次测试求得准确判断目标出现的概率。此种方法不仅实验工作量大，且得到的测量值有限，难以对不同距离处目标的预警率进行量化，本文针对此问题，提出了基于过零数衰减的地震动传感器探测预警分析方法。

1 地震波的传播与预警分析

1.1 地震波的传播规律

目标在地表运动引起地面震动，以地震波的形式沿地表向远处传播。地震波的传播较为复杂，传播过程与环境因素密切相关，易受地形地貌、地质条件和外界因素等干扰。地震波的传播速度受外界环境的影响较大，如在松软的土地中表面波的传播速度约为200m／s，而在硬岩石土地中表面波的传播速度达4 000m／s［5］，但在同种或均质介质中传播时速度是相对稳定的。按照介质质点运动的特点和波的传播规律，地震波可分为体波和面波两大类。Miller和Purssey证明了在半无限介质表面，地面波以Rayleigh波为主，占到总传输能量的70%［6］。波动强度随着传输距离的增加依指数规律衰减，数学表达式为：

式中，α（f）＝ksf，f为信号频率，ks为衰减系数［7］。

1.2 过零分析

过零分析是预警分析的前提，预警分析是建立在过零分析的基础之上。信号的过零分析［8］是指在时域内对信号幅值与门限值比较，计算过零数。信号的过零分析与频谱分析具有密切关系。当信号是频率为f的正弦信号时，过零数为：

过零数与信号的频率成正比，k为比例系数。

对于频率范围从f1到f2的平稳高斯随机信号，单位时间内的过零点数与功率谱G（f）的关系为：

从上式可以看出，若信号主频段频率较高，单位时间内的信号过零点数就较多。

目标运动产生的信号一般都是非平稳随机信号，但在短时间内可以看作平稳随机信号，运用过零分析方法求得一定时间内的过零数。通过对测试的信号进行统计分析，若信号的过零数符合一定统计规律，则可以将目标从背景中区分出来。

1.3 预警分析

预警分析往往是指通过多次测量准确求得目标实际出现的概率，即预警率。通过对测得的地震动信号进行过零分析，得到目标不同距离处一定时间内的过零数及无目标出现时背景地震动信号的过零数，分析目标信号过零数与背景信号过零数的统计规律，设定过零数临界值，当测得的过零数超过临界值时认为目标出现，反之则认为目标没有出现［9］。预警率表达式为：

式中，P（r）为目标在距离r处时的预警率，m为选取的样本次数即目标出现的次数，n为m次样本采样中探测到的地震动信号的过零数超过临界值的次数。

2 过零数衰减模型

由地震波的传播规律和过零分析可知，目标引起的地震波传播距离较近时，各频率信号强度衰减较小，高频信号在过零数的计算中占据主导作用；随着传播距离的增加，信号的强度呈指数衰减，且频率越高，衰减越快，频率较低的信号逐渐成为主频信号，决定过零数的大小，且传播距离越远，主频越低。由式（1）进行计算机仿真可推导出信号主频随传播距离的增加近似依指数规律降低，数学表达式可写为：

式中，fm（r）为信号传播距离r时的主频，km为衰减系数。

由上面分析可知，信号主频在过零数的计算中起决定性的作用。依据信号主频随传播距离的变化关系，结合地震波的振幅随传播距离的增加按指数规律衰减［10］，为简化模型复杂程度，假设目标引起的地震动波在均质介质中传播，探测到的地震动信号的过零数变化只与目标距离有关，可假定过零数的衰减随着目标距离r的增加按指数规律衰减，即

式中，N（r）为距离目标r时测得的地震动信号的过零数，r为目标与传感器间的距离，a，b分别为常数。

通过式（6）可以得到任意距离处目标运动引起的地震动信号的过零数，结合预警率求解公式可对单传感器下目标的预警情况进行定量分析。

3 实验及仿真验证

为了检验本文提出的预警分析方法的有效性，进行了相关的实验研究和仿真计算。

3.1 实验条件和结果

在温度为20～30℃，风速不大于6m／s的条件下，让坦克在土质地面上以25km／h的速度匀速行驶，多次测量得到坦克在距离为400m、350m、250m、150m和50m处的地震动信号，如图1所示。

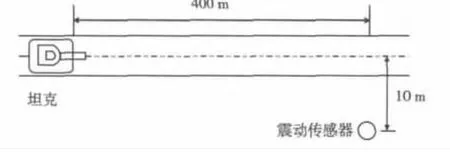
图1 测试示意图Fig.1 The sketch map of experiment

对探测到的坦克地震动信号运用过零分析得到相应距离处的过零数，如表1所示。

表1 坦克地震动信号的过零数Tab.1 The zero－pass number of seismic signal caused by tank

3.2 过零数衰减模型分析

对表1中数据求平均并按式（6）进行拟合，如图2所示。

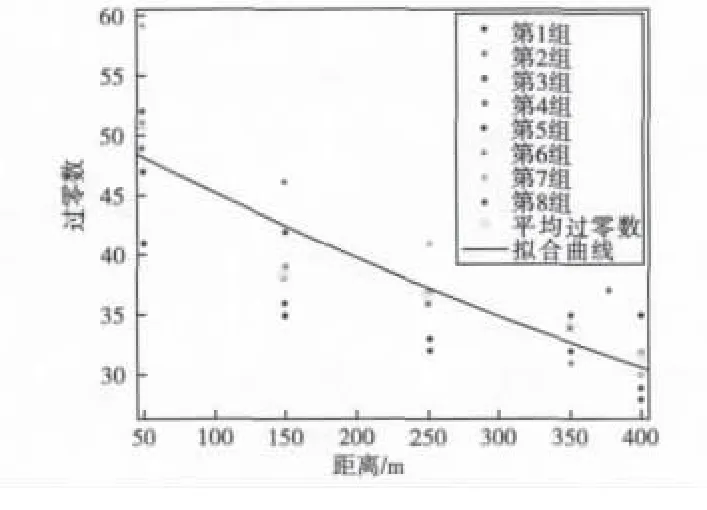
图2 过零数拟合曲线Fig.2 The fitting curve on zero－pass

误差求解公式：

式中，w（r）为在距离r处的过零数误差值，E（r）为在距离r处实验数据所求的的平均过零数，N（r）为在距离r处通过模型求解得到的过零数。

方差求解公式：

式中，D（r）为距离r处的过零数方差，N（i，r）为距离r处第i组数据的过零数值，n为数据组数。

依据式（7）和式（8）可求得目标地震动信号过零数在不同距离处的误差和方差，如表2所示。

表2 不同距离处的误差和方差Tab.2The error and variance at different distances

从表2中可以看出目标地震动信号的过零数误差较小，说明模型的可信度较好；方差随距离的增加近似呈线性递减趋势，如图3所示。通过拟合，可得到地震动信号的过零数方差随距离变化的线性数学表达式：

式中，D（r）为目标在距离r处时过零数方差，c，d都是常数。

图3 过零数方差的拟合曲线Fig.3 The fitting curve on zero－pass variance

3.3 仿真验证

假设目标在任意距离处的地震动信号的过零数服从高斯分布，且以式（6）所求过零数为均值，式（9）所求相应距离处的过零数为方差，运用Matlab软件可求得任意距离处地震动信号的随机过零数（四舍五入取整）。

通过多次求解，结合预警分析式（4），利用蒙特卡洛方法可进一步求得目标在任意距离时的预警率，如图4所示。

图4 预警率随目标距离的变化曲线Fig.4 The curve of warning rate with different target’s distance

依据表1提供的数据和式（4）可以求得坦克目标在50m、150m、250m、350m和400m处的实测预警率分别为100%、100%、100%、100% 和75%，根据本文所提方法求解得到的在相应距离处的预警率分别为100%、100%、98%、85% 和65%，和实测数据计算得到的预警率总体吻合较好。

在目标距离为350m和400m时，预警率的分析结果存在一定差距，主要原因是目标距离已较远，实测地震动信号的过零数在两距离时与选取的临界值相差较小。可通过以下两种方法进行改善，一是在允许范围内适当增加选取的过零数跨度时间来变相增大目标信号过零数与选取的临界值间的差值；另一种方法是选用灵敏度更高的地震动传感器，在距离较远处仍能很好地将目标信号与背景信号区分开来。

从图4中可以看出，随着目标距离的增加，预警率呈递减趋势。目标距离为300m时预警率为96%，300m以后预警率下降的越来越快，目标距离为400 m时，预警率为65%，450m时预警率不到30%，这与现有研究提出的震动预警距离达300～400m相吻合。这主要是因为目标距离较近时，目标信号幅值明显高于过零分析时设定的门限值，此时过零数主要跟随主频变化，表现为预警率高；但随着传播距离的增加，目标信号强度减弱，信号主频降低，背景噪声信号的影响作用更加明显，此时过零数受目标信号主频与噪声信号的双重影响，表现为目标预警率的快速下降；随着传播距离的进一步增加，目标信号逐渐淹没在噪声信号中，导致目标无法被探测到，表现为预警率接近于零或等于零。

4 结论

本文提出了基于过零数衰减的地震动传感器探测预警分析方法，该方法在地震波传播规律和过零数求解的分析基础上，给出了过零数指数衰减模型，可求解任意目标距离时的过零数，结合预警分析得到单传感器对目标一定距离上的量化预警情况。实验及仿真计算结果表明：本文提出的预警分析方法正确反映了预警率随目标距离的变化趋势，且量化结果与实测数据预警分析结果吻合较好。该方法可有效减少实验数据测量的工作强度，获得更多的预警分析数据，并对多传感器组网探测预警距离的分析提供借鉴。

［1］Pakhomov A，Pisano D，Sicignano A，et al.High performance seismic sensor requirements for military and security applications［J］.Proceeding of SPIE，2005，5796：117－124.

［2］谢仕强.基于地震动传感器的人员车辆探测系统［D］.南京：南京理工大学，2006.

［3］Alex Pakhomov，Tim Goldburt.Seismic systems for unconventional target detection and identification［J］.Proceeding of SPIE，2006，6201（1）：1－11.

［4］王永龙.基于无线传感器网络的目标探测技术研究［D］.太原：中北大学，2008.

［5］Slee G E，Ladd M D，McDonald T S，et al.Acoustic and seismic modalities for unattended ground sensors［J］.SPIE，1999，3713：2－9.

［6］邢怀飞，李芳，刘育梁.无线传感器网络声震节点目标分类综述［J］.科学技术与工程，2008，8（7）：1748－1756.

［7］Scholl J F，Agre J R，Clare L P，et al.A low power impulse signal classifier using Harr wavelet transform［J］.Proc SPIE，1998，3577：115－123.

［8］石云波，刘俊，王玲.地面运动目标的震动信号的特性分析［J］.传感技术学报，2007，20（4）：874－876.

［9］陶小亮.基于地震动的目标识别和人员定位算法的研究与实现［D］.南京：南京理工大学，2007.

［10］聂伟荣，朱继南，张元春.地震波传播理论在目标探测中的应用［J］.探测与控制学报，1999，21（4）：50－54.