压缩感知实现方法及应用综述
2014-12-01王红亮刘文怡
王红亮,王 帅,刘文怡
(中北大学电子测试技术国家重点实验室 仪器科学与动态测试教育部重点实验室,山西 太原 030051)
0 引言
随着信息技术的高速发展,需要传输的数据量和采样频率越来越大,因此,科学家遇到“信息瓶颈”的难题:采集时得到的海量数据进行传输和存储,让目前的通信系统越来越难以承受[1]。传统的香农-奈奎斯特采样定理要求采样频率必须大于信号最高频率的两倍以上,才能较好恢复出原信号,虽然实现了信号的采集、压缩和恢复,但采集数据和频率的急剧增加,使这种方法的缺点尤为突出:压缩过程中丢弃了绝大部分采集的数据,增加了额外的存储和传输设备。因此,人们一直寻找解决的办法:采集频率更低,产生的数据量更小,并且能很好地恢复原信号。
近年,Donoho、Candès、Romberg和 Tao在泛函数分析、矩阵理论、统计概率论等基础上提出了新型信号压缩采样的理论,称之为compressive sensing or compressed sensing(简称 CS),中文翻译为压缩感知[2-5]。CS一经提出便吸引许多科学家的关注,因为它解决了香农-奈奎斯特采样定律在信号采集中的不足,而且具有低采样率、低速率和重构质量高等特点,不仅显著降低采集设备和存储设备的设计难度,而且减少设备使用数量。目前,在国内压缩感知理论已成为研究热点,许多科研机构和大学都投入大量的人力、物力开展这方面研究:西安电子科技大学最先建立课题组并将压缩感知理论应用在超宽带雷达信号检测[6-8],取得了非常好的效果,中国科学院在2010年开设压缩感知这门课,而且研究出基于压缩感知的探地雷达数据压缩采集方法,实现了雷达信号的实时采样数据压缩[9]。另外,北京航空航天大学、华南理工大学、解放军理工大学等单位也在积极探索。
1 压缩感知理论
压缩感知的理论分为三个部分:构建稀疏矩阵、设计观测矩阵和重构原始信号。其中判断信号是否具有稀疏性是实现压缩感知的前提;观测矩阵的设计是其重要组成部分,它的设计不仅关系到压缩和采样过程的快慢,而且影响重构信号的准确性;重构原始信号是其核心部分,因此,重构算法是否合适决定恢复原始信号质量的好坏。
1.1 数学模型
假定有限实值离散空间为RN,其中ψi(i=1,2,…,N)是RN的基向量,则空间内任意信号x(N个信息量)表示为:
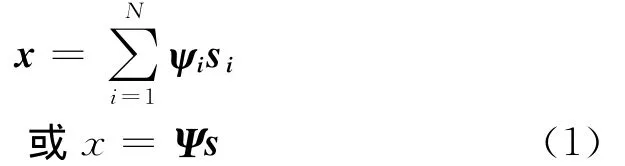
式(1)中Ψ = [ψ1,ψ2,…,ψN],Ψ 是由基向量ψi构成的N×N正交矩阵,如图1所示,矩阵s是信号x在Ψ域的稀疏后的矩阵。
然后采用与Ψ相干性较小的观测矩阵Φ(M×N,M≪N)对信号进行线性投影,过程如图2所示,得到观测矩阵y:

观测值y是M阶列矩阵,注意:在此过程中观测值y不是原信号的采样值,而是信号x在观测矩阵Φ上的投影值。由于信号x是可稀疏的矩阵,所以式(2)可以表示为:
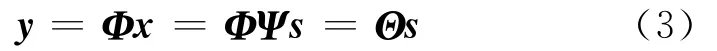
式(3)中Θ(M×N矩阵)称为感知矩阵。
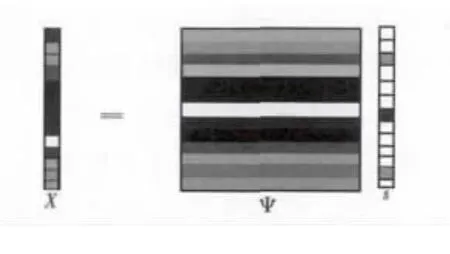
图1 信号稀疏矩阵示意图Fig.1 Sparse Matrix of Signal
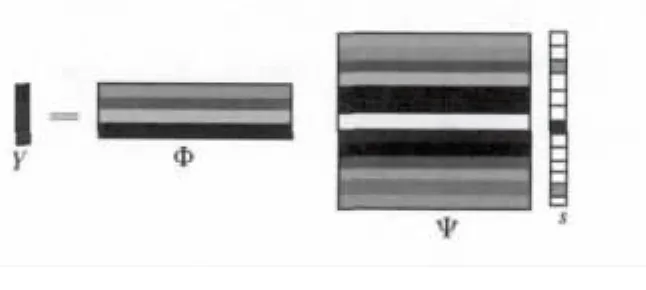
图2 观测过程示意图Fig.2 Measurement Process
从M维观测值y准确地恢复原始信号x最直接的方法是转化为L0范数的最优化问题:
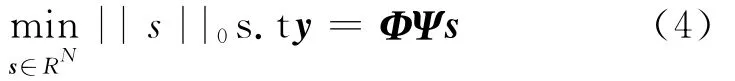
但直接求式(4)的解是个NP-hard问题[5]:利用|s||0虽然可以得出稀疏后的矩阵s内有多少个非零信息,却不知道信息的具体位置,用枚举法有个解(k和N 分别是信号x的稀疏度和信息总量),而N的值一般以万为单位,所以,这种方法找出最稀疏解的难度很大。但Donoho认为最优化问题与信号的稀疏分解类似,从信号稀疏分解的相关理论中寻找更有效的求解途径,证明最小L0范数下在一定条件下和最小L1范数具有等价性可以找到最稀疏的解。所以,式(4)可转化为L1最小范数下的最优化问题:
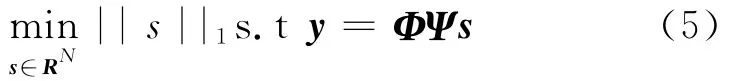
1.2 压缩感知约束条件
压缩感知实现需要满足一些条件:信号在某个变换域是可稀疏,稀疏矩阵和观测矩阵尽量不相干,感知矩阵满足RIP准则等。
1.2.1 稀疏信号
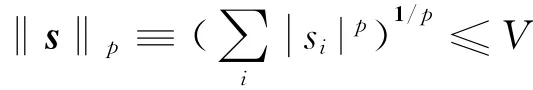
信号x在正交基Ψ稀疏的变换为:s=ΨTx,当0<p<2,实数V>0时,这些系数满足:则说明x在正交矩阵Ψ变换域是稀疏的,如果矩阵s中有k个非零元素(或大系数),则称s为x的k阶稀疏矩阵(稀疏度为k),且k≪N。
1.2.2 相干性
假设有两组正交矩阵Ψ = [ψ1,ψ2,…,ψN],ф=[φ1,φ2,…,φN],两组正交矩阵的相干系数为:
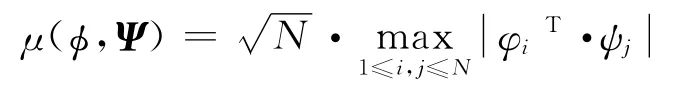
其中φi,ψj是矩阵Φ,Ψ内的第i列和第j列矩阵,根据线性代数所学知识得出相关系数的范围在1≤μ2(Φ,Ψ)≤N,如果这两个矩阵相干系数较小,则矩阵之间的相干性就越小,反之,相干性就越大。正交矩阵Φ,Ψ可做压缩感知的稀疏矩阵和观测矩阵,当μ2(Φ,Ψ)=N时,压缩感知就变成传统的压缩采样。文献[5]推导出M的取值范围:
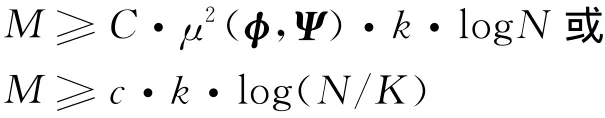
根据前几年研究CS的经验,当M≥4k时,其稀疏性,相干性和重构信号的质量都符合预期[10]。
1.2.3 RIP准则
有限等距准则(Restricted Isometry Property,RIP)是CS理论感知矩阵Θ需要满足重要条件,CS理论的初衷是有效处理复杂信号[11],所以,RIP 准则适合的范围以自然界信号为主。假设一个复杂矩阵Φ(M×N,M≪N),P是Q的子集,其中集合Q={1,2,…,N},Φp是Φ 中随机抽取P 个列向量组成M×P矩阵
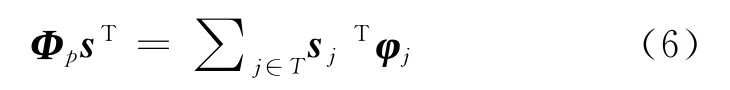
式(6)中矩阵sT为信号稀疏矩阵s的转置,φj为Φp的列向量,Candès and Tao[5]定义k阶稀疏矩阵的限制系数RIC为常数δk且δk∈(0,1)需要满足的条件是:

Candès在文献[12]中证明:当P=2k时,L1范数代替L0范数需要满足的条件δ2s<0.414,但是判断矩阵是否满足RIP准则,以及RIC的计算都是非常困难的,因此相继出现了利用其他理论如相关性判别理论[13]和矩阵Spark判别理论[14]等验证感知矩阵。
1.3 含噪声的压缩感知模型
CS理论应用时,信号常常伴随着噪声和其他因素的干扰,Candès在文献[3][12]提出含噪声的CS模型:

其中z为随机噪声或其他因素干扰产生的变量矩阵,目前,含有噪声处理的方法主要有基追踪降噪法[15]以及转化为二次规划问题解决原始信号恢复[16]。若式(7)满足RIP准则且-1,则可转化为范数L1最优化问题:
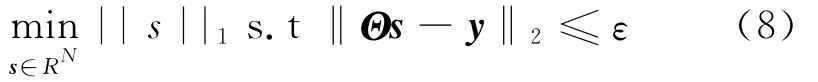
式(8)中ε称为误差值,是理想观测值与实际观测值的差,并且方程的解s′满足:

sk为原信号稀疏矩阵s的k阶稀疏逼近,b1,b2为较小的常量,式(8)中的ε是无噪声下的自身误差值,式(9)中的ε是有噪声和干扰的情况下产生的误差。
1.4 压缩感知与香农采样的区别
压缩感知采集方法并不是对数据直接进行采集,而是通过一组特定波形去感知信号,即将信号投影到给定波形上(衡量与给定波形的相关度),感知到一组压缩数据,最后利用最优化的方法实现对压缩数据解密,估计出原始信号的重要信息[17]。
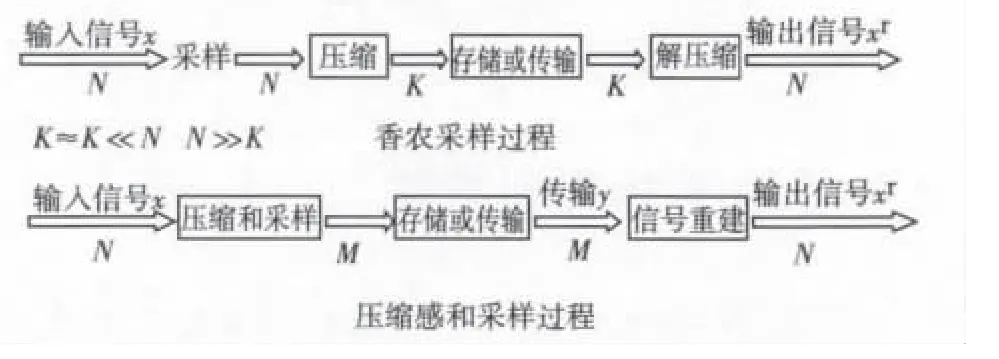
图3 压缩感知和香农采样过程示意图Fig.3 Process of Compressed Sensing and Shannon sampling
如图3所示,香农采样是线性抽样,所以,得到的采样值接近于N个,经过低通滤波器滤除绝大部分,最后只是将剩下的k个抽样值(k≪N)传输或存储,在恢复信号时,利用k个采样值通过带限内插等方法恢复信号xr,其中xr中有N个值。但在这整个过程有个缺点:采样时得到的样本值,在压缩过程中丢弃了绝大部分只剩下k个,所以,采样过程做了很多的“无用功”。
压缩感知和香农采样的区别主要在两方面,一方面,CS是非线性和非自适应性采样,不会随输入信号的频率不同而改变输入装置,不论输入的是声信号,图像信号还是视频信号等都能恢复原信号,只是恢复信号的质量参差不齐。另一方面,CS的采样和压缩同时进行,解决了香农采样中先采集再丢弃的问题。
细心观察图4和图5发现:香农采样其实是压缩感知的特殊形式,只是其观测矩阵是单位矩阵(脉冲函数),压缩感知的观测矩阵是行数远小于列数,但其独特的设计正是压缩感知的优点:信号与观测矩阵相乘最终得到的观测矩阵y远小于原信号。压缩和采样在同一过程,避免了先采样再滤除的问题。
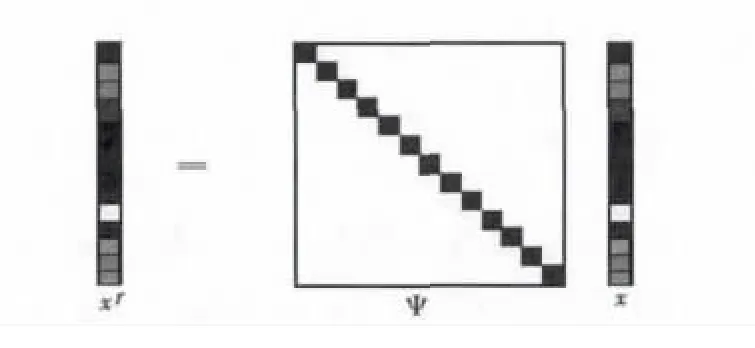
图4 香农采样的矩阵示意图Fig.4 Matrix of Shannon sampling
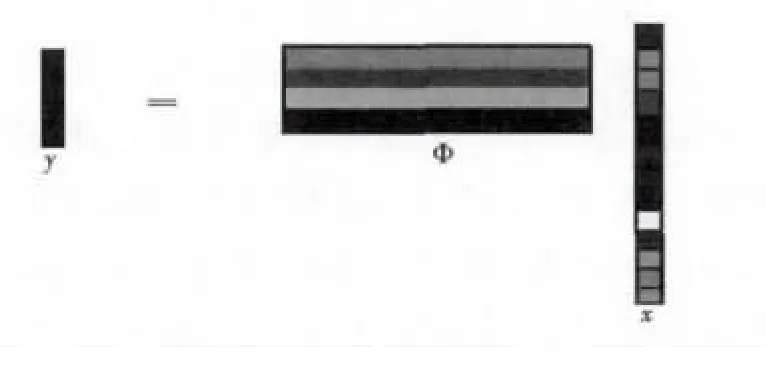
图5 压缩感知采样过程示意图Fig.5 Sampling Process of Compressed Sensing
2 压缩感知实现方法
目前,国内外学者已经提出许多压缩感知实现的方法,本章将这些方法进行归类介绍。
2.1 信号的稀疏
压缩感知模型的前提是信号在变换域是否稀疏,因此,稀疏矩阵的选择影响着信号重构质量的好坏。经过几十年的发展,信号稀疏已经提出多种表示方法,如图6所示,主要分为三大类。第一类是正交基矩阵,利用Fourier变换、离散余弦变换 (Discrete Cosine Transform,DCT)和小波变换(Wavelet)等正交基变换稀疏信号。
第二类是多尺度几何分析法(或者超小波变换法),其中Ridgelet[18],Curvelet[19]和Contourlet[20]等方法应用较多。
在自然图像中包含有大量的纹理特征,线奇异性表现比较突出,小波变换等方法达不到最优的逼近,所以,图像的稀疏就需要其他更有效的方法。Candès等人在1998年提出了变换脊波变换(Ridgelet)以及在此基础提出曲波变换(Curvelet)。Ridgelet变换是沿脊线刻画直线的奇异性,能有效地表示直线的奇异性特征,具有直线奇异性的多变量函数有良好的稀疏性,但对于图像曲线边缘的描述,其稀疏逼近性能只相当于小波变换,不具有最优的非线性逼近稀疏,而且曲线奇异性仍是一个曲线,不是一个点,对于奇异性小波的表示将不是稀疏的。
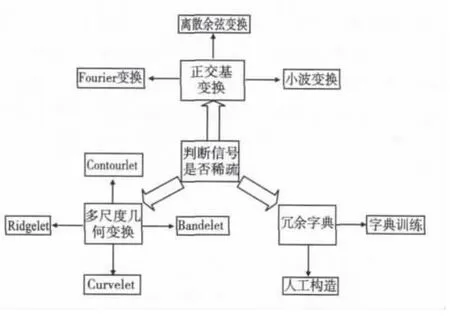
图6 稀疏矩阵的方法示意图Fig.6 Achieve Methods of Sparse Matrix
Curvelet变换的实现是通过一种特殊的滤波过程和多尺度Ridgelet变换,而且在所有可能的尺度上进行Ridgelet变换,这样的曲线波能自适应地“跟踪”该奇异曲线,从而达到非常好的稀疏特性,此方法相对于小波变换的最大优点是具有高度的各向异性,所以,Curvelet变换能更稀疏表达图像信息。
Do等人提出的Contourlet变换是一种多分辨率、局域性和多方向的稀疏表示方法,用类似于轮廓段的基结构稀疏图像,Contourlet变换基的支撑区间是随尺度而变化的“长条形结构”,具有方向性和各向异性,从而使表示图像边缘的Contourlet系数能量更加集中,相比于小波变换Contourlet变换能更“稀疏”地表示图像。
正交基变换的缺点是:信号的稀疏变换唯一,如果正交基选择不合适,不能得到最稀疏的矩阵,进而影响信号重构,同时这类方法对高维信号如图像和视频信号等不适用。多尺度几何分析法以“最优”图像表示理论为基础,主要解决了高维空间数据稀疏表示的问题,却仅对高维信号有很好的效果,一维信号不能得到最稀疏的解。
针对上述两类方法的优缺点,由Mallat和Zhang在1993年提出了全新的稀疏理论——冗余字典(或称过完备字典),而且指出冗余字典对于信号稀疏表示的必要性和重要性,最后,介绍了匹配追踪(Matching pursuit,MP)算法。冗余字典仍是目前信息领域研究的难点和热点,其主要内容:将空间RN的N个基向量增加到N+P个(P为正整数),兵器矩阵的任意N个列向量不相关,字典中可能既有Fourier变换基同时有Curvelet变换基等,需要遵循一个原则:各个基向量尽可能使输入信号达到最稀疏。基于这种原则,冗余字典一定是非正交而且是冗余的,正是通过增加基向量个数提高变换系统的冗余性增强信号逼近的灵活性,从而提高稀疏表示高阶信号的能力。根据能量守恒定理,信号原有的能量没有发生转移且大小不变,则稀疏后的信号会呈现在极少位置的系数非常大,绝大部分位置系数基本为零。
冗余字典可以使信号呈现最佳稀疏,其设计方法有人工构造和字典训练两类,目前人工构造应用较为广泛,其构造冗余字典主要思想是:利用参数和含参数的函数中选取若干函数来近似表示信号,参数的选取是字典设计中一个很重要的问题。经典的方法有Gabor字典[21],Refinement-Gaussian混合字典[22]和Gabor感知多成分字典[23]等。字典训练是近几年提出的,使用较多的有K-SVD算法[24]及在此基础提出的 EK-SVD[25],DK-SVD[26]等,这种方法的优点是稀疏表示效果较好,计算复杂度较低,但缺点是没有完备的理论支撑。
2.2 观测矩阵的设计
压缩感知理论模型中,观测矩阵在信号稀疏和信号重构中起关键性的作用。如图7所示,现在的观测矩阵设计分为两大类:随机观测矩阵和确定性观测矩阵。
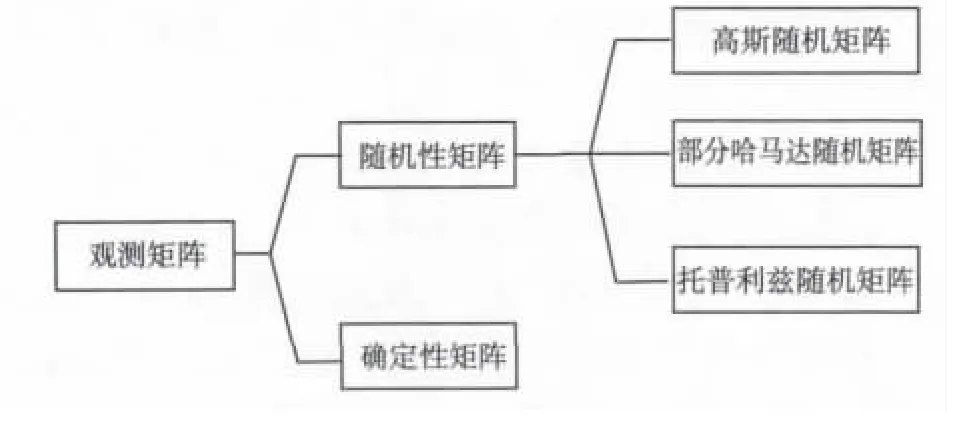
图7 设计观测矩阵的方法Fig.7 Achieve Methods of Measurement Matrix
2.2.1 随机观测矩阵
观测矩阵设计的原则是与稀疏矩阵尽可能不相干,同时,自身的列矩阵之间相互独立。目前,随机矩阵如随机高斯矩阵[2,5]、部分哈马达随机矩阵[27]和托普利兹矩阵[28]等采用较多,其中符合独立正太分布的高斯随机矩阵最具有代表性。这些随机矩阵的共同点是:列矩阵之间保持非常好的相互独立性,同时随机矩阵与稀疏矩阵有非常小的相干性,精确重建所需的观测次数较少而且符合RIP准则,所以,此方法在软件仿真时非常受“欢迎”,但因为其自身的不确定性很难在硬件电路实现,这也是令人“惋惜”的地方。
2.2.2 确定性观测矩阵
Ronald A.Devore最先提出了符合RIP准则的多项式确定性观测矩阵,解决了随机观测矩阵的不足。简单叙述构造确定性观测矩阵的步骤[29]:
假设存在有限元素个数为z的集合T,T中的元素取值范围为{0,1,2,…,z-1}。给定任意正整数d,0<d<z,用Pc来表示最高次幂小于或等于c的多项式集合:H(x)=a0+a1x+…+acxc,其中H(x)的系数{a0,a1,…,ac}的取值范围为集合T,即a0,a1,…,ac∈T,所以,共有N =zc+1个多项式。定义大小为z×z的零矩阵F,即矩阵F的元素值全为0。且记矩阵F的位置为{(0,0),(0,l),(0,2),…,(z-1,z-2),(z-1,z-1)}。
首先,在矩阵F的每一列的某一个位置插入数值1。其插值方式如下:把x到H(x)当作是T到T的映射,即多项式H(x)的自变量和函数都在集合F中取值,矩阵F的第x列第H(x)个位置的值由0变成1。
然后,把矩阵F转换为大小为M×l的列向量VH,其中M=z2。在向量VH中,从第一个位置开始,前z个元素中有1个1,前2z个元素中有2个1,以此类推,在列向量VH中共有p个1。
循环上述两个步骤直到取完所有多项式系数后,共有一个这样的列向量。由这N个列向量组成的矩阵记为Φ0,大小为M×N,M=z2,N=zc+1。而且,文献[30]证明上述确定多项式观测矩阵符合RIP准则。
多项式确定性观测矩阵也有缺陷,如观测值M的取值范围比随机矩阵的设计时间比较长,观测矩阵不够稀疏等,但它可以在硬件电路中实现,而且有广阔的应用前景,这些都是随机观测矩阵没有的优点。
2.3 重构信号算法
重建算法的设计应该遵循如下基本准则:算法应该利用尽量少的压缩测量,并且快速、稳定、精确或近似精确地重建原始信号。重构算法有两大类应用较为广泛:松弛法和贪婪算法。
2.3.1 松弛法
Donoho提出利用L1范数代替L0范数,变成线性规划的凸优化问题[31],找出最稀疏的矩阵恢复原信号,这种方法称为松弛法。
如图8用二维平面表示Lp范数球在0<p<1,p=1,p=2的稀疏求解问题。当p=0,利用范数L0求最稀疏矩阵的解是NP-hard问题。当0<p<1时,范数Lp本身不是凸函数,而且所得到最稀疏的解不唯一。当p=1时,范数L1是凸函数,约束于y=Φx直线上转化为线性规划的凸优化问题,最稀疏解在坐标轴是唯一的,其他坐标轴的坐标为0。当p=2时,得到的唯一解是与y=Φx直线相切的点,且不在坐标轴上,所以这个解不是最稀疏的。
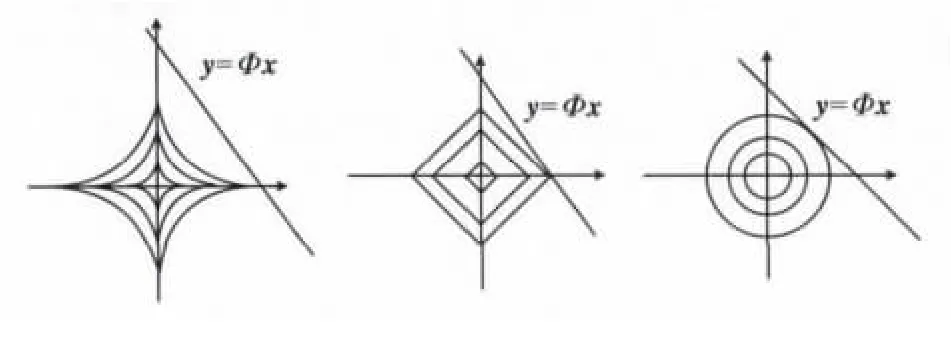
图8 三种Lp范数球的2D示意图Fig.8 Three Kind of 2Dgraph of Norm Lpball
虽然利用L1范数代替L0范数可以求解最稀疏的矩阵,但要满足RIP准则、稀疏性、一致不确定性和弱准确重构等条件,但是利用L1范数求解也存在个问题:如果y=Φx满足斜率为45°,稀疏解有无穷多个,所以,应近尽量避免这种情况。L1范数最小化是利用基追踪BP[32]的优化求出最小值,解决BP线性规划的凸优化问题应用较多的方法有内点法、梯度 投 影 法 (Gradient Projection for Sparse Reconstruction,GPSR)、 同 伦 算 法 (Homotopy Algorithm,HA)[33]和 最 小 角 度 回 归 法 (Least Angle Regression,LARS)[34]。这类方法优点是重构信号的质量较好,需要观测的个数较少,缺点是计算复杂度较高。
2.3.2 贪婪算法
贪婪算法的主要思想是:每一步迭代都选择最匹配的原子,直至逼近原信号。这类方法有匹配追踪(MP)法、正交匹配追踪(OMP)法以及在此基础上的正则正交匹配追踪(Regularize Orthogonal Matching Pursuit,ROMP)[35]和压缩感知匹配追踪 (Compressed Sampling Matching Pursuit,CoSaMP)[36]和阈值迭代法[37]等,其中OMP算法最具代表性。
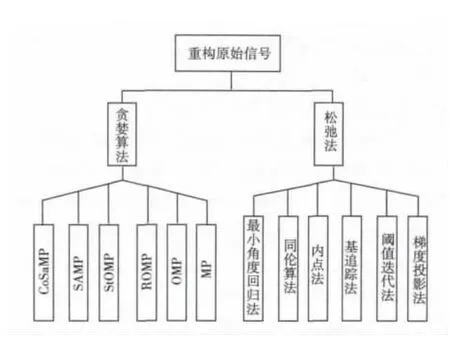
图9 重构信号的算法示意图Fig.9 Signal Algorithm of Recovery Signal
下面简单叙述OMP算法:
输入:感知矩阵Φ,测量向量y,稀疏度k;
输出:x的k稀疏的逼近xr,重建误差r;
初始化:余量r0=y,重建信号x0=0,索引集Γn=Γn-1∪ {k},迭代次数n=0;
步骤1:计算余量和感知矩阵Φ的每一列的内积gn=ΦTrn-1;
步骤2:找出gn中元素最大的元素,j=argmax|gn[i]|;
步骤3:更新索引集Γn=Γn-1∪ {j}及原子集合 ΦΓn = ΦΓn-1∪ {φj};
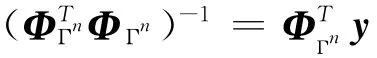
步骤5:更新余量rn=y-Φxn;
步骤6:判断是否满足停止条件,满足则停止,xr=xn,r=rn输出xr,xn,否则转步骤1。
贪婪方法的计算复杂度虽然较低,但与松弛法相比,需要将原始信号内的N个元素逐一恢复,而且重构时每次恢复的计算都有微小误差,每个元素的误差的叠加最终也会变成非常可观的值,同时,需要较多的观测次数,所以,重构信号的质量也相对较低。
3 压缩感知应用
目前,压缩感知在各个领域的应用成果不断涌现,CS起源于对核 磁 共 振 (Magnetic Resonance Imaging,MRI)成像的研究,同时,在超声探测图像、遥感成像和光学成像等方面进展迅速。此外,CS在语音信号的稀疏和去噪、信道编码数据传输、雷达检测等方面也在不断深入。
3.1 图像方面
在光学成像领域,首先将CS理论应用于实践的是Rice大学的Baraniuk教授等研发的“单像素相机”[30],如图10所示,相机主要利用数字微镜阵列(Digital Micromirror Array,DMA)完成了目标图像在伪随机而至模型的线性投影,通过单一信号光子检测器采样,取得远小于香农采样的像素点恢复图像,同时,具有自适应图像波长的能力。在医学成像领域,Lustig提出的稀疏 MRI成像[38]是最早将CS应用于医学成像,通过空间的部分数据完美恢复出原始图像,而且,提高了MRI的成像速度,减少对人体的辐射时间,从而降低危害。清华大学的焦鹏飞等提出将CS应用于CT成像[39],减少了采集图像数据量,恢复的图像更加清晰。此外,Ronen Tur在2010年提出了基于有限更新率的压缩感知超声成像算法[40]。所以,CS在三维图像、脑部成像和超声图像检测等方面有较大的应用前景。
3.2 语音方面
目前,国内外将压缩感知理论应用在语音信号处理才刚刚开始,相对于其他领域的研究成果也相对较少。语音信号压缩感知理论的研究主要集中在语音信号稀疏基、语音增强和语音编码三个方向。

图10 Rice大学的单像素相机结构图Fig.10 Structure of Single Pix Camera
Giacobello等[41]利用语音信号冗余域的稀疏性,特别是浊音信号的稀疏性,通过压缩感知计算稀疏的线性激励的近似值,然后再进行编码,并与多脉冲激励等方法进行对比,实验结果表明取得较好的听觉效果。该文献也提出CS可以应用到非正交基上具有稀疏性的语音信号。同时,语音信号自适应方面的研究开始受到关注,通过相应自适应算法能更好将语音信号稀疏、去噪和编码[42]。此外,压缩感知理论还应用到语音信号处理的其他方向:语音信息隐藏、语音丢包补偿策略和欠定盲源分离等。随着压缩感知理论研究的不断深入,有关语音信号方面的成果也会不断涌现。
3.3 模数转换
CS应用在模/数转换是近几年研究的难点,针对这个问题,较为成熟是S.Kirolos,J.Laska在2006提出的模拟信息转换器(Anology to Information convertor,AIC)[43](结构如图11)。模拟信息转换器主要原理是:采用一组具有信号Nyquist频率的随机序列对待测试信号进行随机解调,将高频模拟信号投影到基带采样,利用重构算法恢复原始信号。Cande’s在AIC基础上研究出RMPI压缩采样芯片[44],同时出现多通道的AIC宽带转换器 (Modulated Wideband Conversion,MWC)[45]。文献[46]建立了并行多通道的AIC声音信号压缩感知模型,通过大量的相关实验得出结论:多路AIC很好的满足RIP准则和非相干性,同时,多通道恢复信号的质量远好于单通道。目前,这种模型已成功运用在逆合成孔径雷达、穿墙雷达和探地雷达等雷达探测领域,并取得了预期的结果[47]。
4 压缩感知的展望
压缩感知理论的出现为信息领域带来一次新的“革命”,改变了传统压缩采样信号的模式,减少了采集海量冗余数据造成存储和传输设备的使用量,而且降低不断接近采集设备极限的抽样频率。不过,该理论刚刚提出,在应用时也有需要改进的方面:
1)去噪方面
虽然CS在压缩采样过程可以去除部分噪声,但观测值进行传输、存储和恢复原信号时,也会产生大量的噪声,目前的方法是采用滤波器,但会造成相位偏移和衰减等问题,所以,设计观测矩阵和恢复算法尽量减少噪声是目前研究的新趋势。
2)自适应观测矩阵设计方面
观测矩阵需要满足RIP等条件,大多采用随机性观测矩阵,但随机矩阵在硬件实现非常困难,而且不具有普遍适用性。所以,有必要建立自适应观测矩阵,不仅在硬件电路中可以实现,并且对不同的信号(如语音、图像)进行自适应压缩采样。
3)低速模数转换方面
压缩感知的应用领域绝大部分是针对数字信号,虽然模/数转换虽然采用AIC可以实现,但先利用奈奎斯特定律进行高速采样,再利用CS方法低速处理恢复原信号,能否利用ADC低速采样进行压缩感知方法恢复信号。
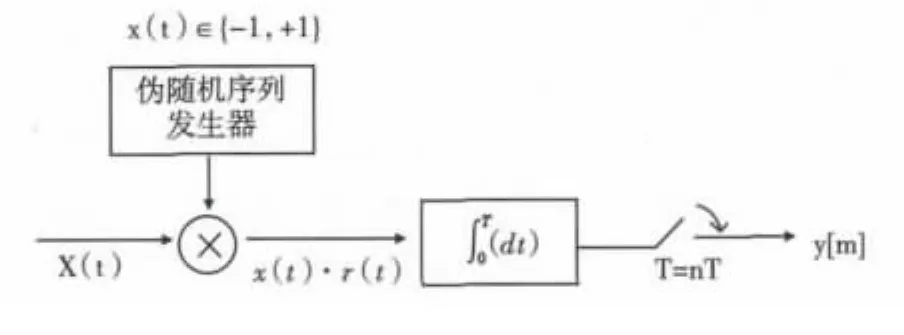
图11 AIC结构模型Fig.11 Structure Model of AIC
5 结论
压缩感知理论基于信号可稀疏性原理,通过将信号从高阶矩阵线性投影为低阶矩阵的方法实现压缩采样。与传统香农采样定理相比,具有采样速率远低于奈奎斯特采样频率,压缩和采样过程同时进行等优点。本文简述了压缩感知的基本理论,重点介绍了稀疏矩阵、观测矩阵和重建算法的研究进展和限制条件。虽然该理论存在非自适应采样等缺陷,但在核磁共振、雷达探测和语音编码等领域取得了较好的效果,而且在医疗三维成像、超声图像检测等方面具有良好的发展前景。但该理论还有待进一步研究和验证,以满足各种实际应用需要。
[1]Richard G.Baraniuk.More Is Less:Signal Processing and the Data Deluge[J].Science,2011,331:717-718.
[2]David L Donoho.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[3]ECandès,Wakin M.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.
[4]Donoho David L,Tsaig Y.Extensions of compressed sensing[J].Signal Processing,2006,86(3):533-548.
[5]Candès E,Romberg J,Tao Terence.Robust uncertainty principles:exact signal reconstruction from highly in-complete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[6]焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7);1651-1662.
[7]石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报2009,37(5):1070-1081.
[8]Shi G,Lin J,Chen X,Qi F,et al.UWB Echo Signal Detection With Ultra-Low Rate Sampling Based on Compressed Sensing[J].IEEE Trans.on Circuits and Systems II:Express Briefs,2008,55(4):379-383.
[9]卢策吾,刘小军,方广有.基于感知压缩的探地雷达数据压缩采集[J].电子学报,2011,9(39):2201-2206.
[10]Ventura R,Vandergheynst P,Frossard P.Low-rate and flexible image coding with redundant representations[J].IEEE Trans.Image Processing,2006,15(3):726-739.
[11]MElad,Bruckstein A M.A generalized uncertainty principle and sparse representation in pairs of bases [J].IEEE Transactions on Information Theory,2002,48(9):2558-2567.
[12]Candès E.compressive sampling[C]//Madrid,Spain:Proceedings of the International Congress of Mathematicians,2006:1433-1452.
[13]Donoho D L,Huo X.Uncertainty principles and ideal atomic decomposition[J].IEEE Transactions on Information Theory,1999,47(7):2845-2862.
[14]MElad,Bruckstein A M.A generalized uncertainty principle and sparse representation in pairs of bases[J].IEEE Transactions on Information Theory,2002,48(9):2558-2567.
[15]Chen S S,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing,2001,43(1):129-159.
[16]Boyd S P,Vandenberghe L.Convex Optimization[M].Cambridge:Cambridge University Press,2004.
[17]戴琼海,付长军,季向阳.压缩感知研究[J].计算机学报,2011,3(34):425-434.
[18]Candès E.Ridgelet:Theory and Application[D].California:Stanford University,1998.
[19]Candès E,Donoho D L.Curvelets[R].California:Stanford University,1999.
[20]Pennec E,Mallat S.Sparse geometric image representations with bandelet[J].IEEE Trans.Image Process,2005,14(4):423-438.
[21]Bergeau F,Mallat S.Match pursuit of images[C]//Proceedings of IEEE Signal Processing.Philadelphia,USA:IEEE ComputerSociety,1994:330-333.
[22]Ventura R,Vandergheynst P,Frossard P.Low-rate and flexible image coding with redundant representations[J].IEEE.Trans.Image Processing,2006,15(3):726-739.
[23]Sun Y B,Xiao L,Wei Z H,et al.Sparse representations of images by a multi-component Gabor perception dictionary[J].Acta Automatica Sinica,2008,34 (11):1379-1387.
[24]Michal A,Elad M,Alfred B.K-SVD:An algorithm for designing over-complete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing,2006,54(11):4311-4322.
[25]Mazhar R,Gader P D.EK-SVD:Optimized dictionary design for sparse representations[C]//19th International Conference on Pattern Recognition,2008:1-4.
[26]Zhang Q,Li B X.Discriminative K-SVD for dictionary learning in face recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR),2010:2691-2698.
[27]Tsaig Y,Donoho D,Extensions of compressed sensing[J],signal Processing,2006,86(3),549-571.
[28]Holger Rauhu.Circulant and Toeplitz matrices in compressed sensing[J].In Processing SPAR’09,Saint Malo,2009.
[29]Ronald A.Devore.Deterministieeon struetions of compressed sensing matrice[J].Journal of ComPlexity,2007,23(4-6):918-925.
[30]Duarte M F,Davenport M A,Takhar,et al.Single-pixel imaging via compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):83-91.
[31]David Donoho.For most large underdetermined systems of linear equations,the minimal ell-1norm near-solution approximates the sparsest near-solution[J].Communications on Pure and Applied Mathematics,2006,59(7):907-934.
[32]Chen Shaobing,Donoho D L,Saunders M A.Atomic decomposition by dasis dursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61.
[33]Malioutov D M,Cetin M,Willsky A S.Homotopy continuation for sparse signal representation[C]//IEEE International Conference on Acoustics,Speech,and Signal Processing.Philadelphia,USA:IEEE Press,2005:733-736.
[34]Efron B,Hastie T,Johnstone I,et al.Least angle regression[J].The Annals of Statistics,2004,32(2):407-451.
[35]Needell D,Vershynin R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J].Foundations of Comp.Math,2000,9(3):317-334.
[36]Needell D,Tropp J.Cosamp:Iterative signal recovery from incomplete and inaccurate samples[J].Applied and Comput.Harmon.Anal.2009,26(3):301-321.
[37]Daubechies I,Defrise M,Mol C De.An iterative thresholding algorithm for linear inverse problemswith a sparsity constraint[J].Comm.Pure.Appl.Math,2004
[38]Lustig M,Donoho D,Pauly J M.Sparse MRI:The application of compressed sensing for rapid MR imaging[J].Magnetic Resonance in Medicine,2007,58(6):1182-1195.
[39]焦鹏飞,李亮,赵骥.压缩感知在医学图像重建中的最新进 展 [J].CT 理 论 与 应 用 研 究,2012,21(1):133-147.
[40]Tur R,Eldar Y C,Friedman Z.Innovation rate sampling of pulse streams with application to ultrasound imaging[J].IEEE Transactions on Signal Processing,2011,59(4):1827-1842.
[41]Giacobello D,Christensen M G,Murthi M N,et al.Retrieving sparse patterns using a compressed sensing framework:applications to speech coding based on sparse linear prediction[J].Signal Processing Letters,IEEE,2010,17(1):103-106.
[42]罗武骏,陶文凤,左加阔,等.自适应语音压缩感知方法[J].东 南 大 学 学 报 (自 然 科 学 版 ),2012,42(6):1027-1030.
[43]Kirolos S,Ragheb T,Laska J N,et al.Practical issues in implementing analog-to-digital converters[J].International Workshop on System-on-Chip for Real-Time Applications,2006:141-146.
[44]Becker S,Bobin J,Candès E J,NESTA:a fast and accurate first-order method for sparse recovery[J].SIAM J.Imaging Sci.2011,4(1):1-39.
[45]Mishali M,Eldar Y C.From Theory to Practice:Sub-Nyquist Sampling of Sparse Wideband Analog Signals[J].IEEE Journal of Selected Topics on Signal Processing,2010,4(2):375-391.
[46]余恺,李元实,王智,等.基于压缩感知的新型声信号采集方法[J].仪器仪表学报.2011,33(1):106-112.
[47]刘记红,徐少坤.压缩感知雷达成像综述[J].信号处理,2011,27(2):251-260.
