基于决策表分解的属性约简算法

刘旭东，秦亮曦

（广西大学 计算机与电子信息学院，广西 南宁530004）

0 引 言

属性约简的方法很多，但所追求的目标相同，就是能够高效获得最小约简集。然而，找到最小约简是一个NP－hard问题，通常采用基于属性重要度等启发式搜索算法找到最优或次优约简集，所以如何高效的获得约简结果是属性约简算法的研究重点。当数据集较大时，现有一些基于属性重要度的约简算法效率往往比较低。针对这一问题，本文提出了一种基于决策表分解的属性约简算法，不仅能得到较优的约简集，更能降低时间复杂度，较快地得到约简结果。

1 粗糙集理论的基本概念［1，2］

定义1 决策表信息系统用S＝（U，C∪D，V，f）来表示，其中，U表示一个有限非空对象集 （论域），U ＝ ｛0，1，2，…，n｝；C为条件属性集，D为决策属性集，通常决策属性只有一个，且C∩D＝；V＝∪Va，Va为属性a的值域；f为信息函数f：U×（C∪D）→V，a∈（C∪D），x∈U，有f（x，a）∈Va。

定义2 令P C∪D ，ind（P）＝ ｛（x，y）｜f（x，a）＝f（y，a）， a∈P｝称为S的不可区分关系。显然，不可区分关系是一个等价类。属性集P将论域U划分为多个等价类，记为U／P。

定义3 对于决策表信息系统S，令U／C＝ ｛X1，X2，…，Xn｝，U／D ＝ ｛Y1，Y2，…，Ym｝。条件属性C 关于决策属性D 的正域POSC（D）＝∪ ｛Xi｜XiYj，Xi∈U／C，Yj∈U／D｝。正域基数是衡量属性重要度的一个重要准则。

定义4 对于决策表信息系统S，若POSP（D）＝POSC（D）， 且 对 于 a ∈ P， 有 POSP（D） ≠POS｛P－a｝（D），则称P是S的一个属性约简。

定义5 若存在2个对象x，y，若 a∈C，f（x，a）＝f（y，a），且f（x，D）≠f（y，D），则称S是不相容决策表，即当2个对象条件属性相同，但分类不一样时，此信息系统是不相容决策表，否则就是相容决策表。本文只考虑相容决策表。

定义6 互信息I（X，Y）是一个用来测量2个随机变量X，Y之间相关程度的量，I（X，Y）其中，p（x，y）表示随机变量X、Y的联合分分别是变量X、Y的边缘分布。

定义7 在决策表信息系统S＝ （U，C∪D，V，f）中，有属性集P C，添加一个属性p∈C到P中，获得的互信息增加量 （信息增益）为gain＝I（P∪p，D）－I（P，D）。计算每个条件属性对决策属性的gain，gain越大，条件属性就越重要。

2 基于决策表分解的属性约简算法及其复杂度分析

2.1 算法思路

一般采用启发式算法进行属性约简，定义一个启发函数，如差别函数（区分函数）［3，4］或属性重要度函数［5－11］，通过此函数进行属性约简。在基于差别函数的属性约简算法中，需要通过比较对象之间的差异来构造决策表信息系统的区分矩阵，当数据集比较大时，空间和时间复杂度都比较高，所以一般采用定义属性重要度函数的启发算法。在基于属性重要度的属性约简算法中，传统的约简算法（如文献 ［5］）建立在整个决策表上，通过划分等价类U／P，不断计算POSP（D）是否等于POSC（D）。只有当等价类中的所有对象决策属性值相同时，这些对象才属于正域。也就是说，只要存在2个对象，其决策属性值不同，那么整个等价类都不属于正域，此时，就不用考虑其它对象。经过研究，在选取某个最重要的属性后，在下一步的迭代过程中，可以在上一次所求的各个等价类中分别计算正域，而不必在整个决策表上计算，并且如果其中一些等价类已经在正域中，就可以忽略这些等价类。由于每次计算是建立在已分解的决策表上，所以不需要计算对属性集的正域基数，每次迭代只需计算对单个属性的正域基数，而且每次迭代所处理的对象将大大减少。由此设计出一个基于决策表分解的属性约简算法，该算法的主要思想是在每次迭代选取一个最重要的属性后，将原有决策表按照所求的等价类分解成各个更小的决策表。

从包含很多条件属性的决策表信息系统中得到约简结果，通用方法是在每次迭代过程中挑选最重要的属性直到找到一个合适的约简集。衡量属性重要性有很多准则：正域基数，信息熵，互信息增益等。在传统的属性约简算法中，一般只采用单一的评价标准来衡量属性的重要度，如基于信息熵的属性约简算法［5］一般以信息熵为评价标准，每次迭代选取信息熵最小的属性；基于正区域的属性约简算法［6－10］通常以正域基数为评价标准，每次迭代选取正域基数最大的属性。当存在多个属性其衡量标准相同时，采用单一的标准就无法判别，只能随机的选取其中某个属性，进而影响最终约简结果。本文提出的基于决策表分解的属性约简算法采用正域基数和互信息增益相结合的方法来衡量属性的重要度。由定义3知，属性p关于决策属性D的正域POSp（D）中个数越多，表明正域中不可分辨的对象个数越多，D对p的依赖度越大，属性就越重要。由定义7知，添加一个属性后，获得的信息增益越大，表明这个属性给分类系统带来的信息就越大，该属性就越重要。本文提出的属性约简算法在每次迭代过程中，选取正域基数最大的属性，当存在正域基数相同时，再选取互信息增益较大的，这样能更客观地衡量属性的重要度，从而得到更小的约简结果。当两者都相同时，说明属性是同等重要的，则随机选取一个。

2.2 算法描述及复杂度分析

输入：S＝ （U，C ∪ D，V，f）

输出：约简结果RES

1.for每个条件属性p∈C，do

1.1.for（每个决策表 （第一次只有一个决策表）），do

求出等价类U／p，然后根据等价类计算正域POSP（D），对正域进行累加。

2.选取正域基数最大的属性p放入RES中。若正域基数最大的属性存在多个，则先根据等价类求出互信息增益，再选取互信息增益最大的属性p放入RES中。若互信息增益也相等，则选取序号靠前的属性。

3.分解决策表for（U／p中每个等价类），do

3.1.if（等价类不在正域中）｛

构造新决策表：对象集为等价类中的元素，条件属性去除p，决策属性不变；｝

4.如果决策表不为空，则转到第1步 （决策表已经被分解），否则，终止。

算法的时间复杂度分析：划分等价类的时间复杂度为O （｜U｜）［6，8］，所以第1步计算正域的时间复杂度为O（｜C｜｜U｜）；求信息增益的时间复杂度为O （mn），其中，m是条件属性p的种类，n是决策属性的种类 （mn＜＜｜C｜｜U｜），所以第2步的时间复杂度最坏情况下为O （｜C｜）；第3步的时间复杂度为O （｜U｜），所以每层递归的时间复杂度为O （｜C｜｜U｜）。由于每层递归要处理的对象数目｜U｜不断减小，条件属性个数｜C｜也不断减少。当不存在冗余属性时，需要递归｜C｜次，所以最坏情况下，时间复杂度为O （｜C｜2｜U｜）。

2.3 实例分析

在表1中，有7个对象，4个条件属性a，b，c，d，一个决策属性e。先划分等价类，ind（｛a｝）＝ ｛｛0，2，3，4，5｝，｛1，6｝｝，ind（｛b｝）＝ ｛｛0，2，3｝，｛1，6｝，｛4，5｝｝，ind（｛c｝）＝｛｛0，6｝，｛1，2，3，4，5｝｝，ind（｛d｝）＝ ｛｛0，3，5｝，｛1，4，6｝，2｝，ind（｛e｝）＝ ｛｛0，5｝，｛1，3｝，｛2，4，6｝｝。通过等价类计算正域，POS｛a｝｛e｝＝，POS｛b｝｛e｝＝，POS｛c｝｛e｝＝，POS｛d｝｛e｝＝ ｛2｝。 所以选取属性 d， 得 RES ＝ ｛d｝。U／｛d｝＝ ｛｛0，3，5｝，｛1，4，6｝，｛2｝｝，构造2个新决策表，见表2、表3。

表1 决策表S

表2 决策表S1

表3 决策表S2

在决策表S1和S2中，先划分等价类，对S1：ind（｛a｝）＝ ｛｛0，3，5｝｝，ind（｛b｝）＝ ｛｛0，3｝，｛5｝｝，ind（｛c｝）＝ ｛｛0｝， ｛3，5］｝，ind（｛e｝） ＝ ｛｛0，5｝， ｛3］｝； 对 S2：ind（｛a｝）＝ ｛｛1，6｝，｛4｝｝，ind（｛b｝）＝ ｛｛1，6｝，｛4｝｝，ind（｛c｝）＝ ｛｛1，4｝，｛6｝｝，ind（｛e｝）＝ ｛｛1｝，｛4，6｝｝。

再计算正域：POS｛a｝｛e｝＝＋｛4｝＝ ｛4｝；POS｛b｝｛e｝＝｛5｝＋｛4｝＝ ｛5，4｝；POS｛c｝｛e｝＝ ｛0｝＋｛6｝＝ ｛0，6｝。b，c的正域基数相等，计算信息增益，gain（b）＝0.2516，gain（c）＝0.2516。于是，选取属性b，RES ＝ ｛d，b｝。U／｛b｝＝｛｛0，3｝，｛5｝，｛1，6｝，｛4｝｝，再构造新决策表，见表4、表5。

在决策表S11和S21中，对S11：ind（｛a｝）＝ ｛｛0，3｝｝，ind（｛c｝）＝ ｛｛0｝，｛3｝｝，ind（｛e｝）＝ ｛｛0，3｝｝；对S21：ind（｛a｝）＝ ｛｛1，6｝｝，ind（｛c｝）＝ ｛｛1｝，｛6｝｝，ind（｛e｝）＝｛｛1｝，｛6｝｝。再计算正域，POS｛a｝｛e｝＝ ｛0，3｝＋＝ ｛0，3｝；POS｛c｝｛e｝＝ ｛0，3｝＋｛1，6｝＝ ｛0，3，1，6｝。所以取属性c，RES＝｛d，b，c｝。此时，没有构造决策表的对象，故算法终止。约简结果是 ｛d，b，c］。

表4 决策表S11

表5 决策表S21

3 实验分析

收集UCI数据库中8个数据集对文献 ［5］中的算法（原算法）和本文提出的算法 （改进算法）进行对比测试。算法用C＋＋编写，实验环境为 Windows XP，Pentium4 3.0GHz，512M内存，Code：Blocks10.05。数据集规模见表6。

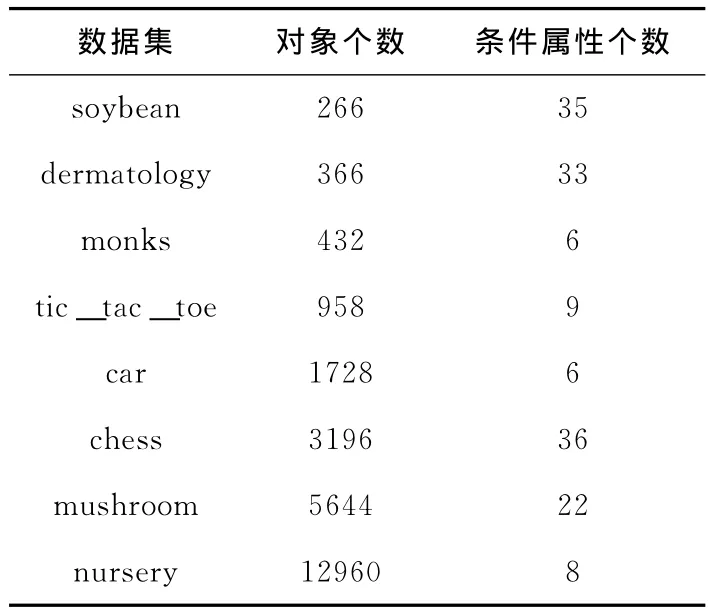
表6 数据集

为了不影响测试结果，mushroom数据集中去掉了含有缺失值的对象。如果是连续型数据，则先进行离散化处理。由于不同数据集运行时间的跨度比较大，所以把实验结果放在2个图中。实验结果如图1，图2，表7所示。由表7知，改进算法与原算法得到的约简结果相同，说明改进算法是正确可行的。由图1，图2知，在运行时间上，改进算法比原算法都得到了不同程度的提高，其中mushroom提高的幅度最大，原算法需要25.469s，改进算法只要0.578s。原算法随着数据集的增加，运行时间逐渐增加，但改进算法的运行时间不一定。比如，mushroom比chess大，但时间明显要少于chess，主要原因有2点：①mushroom中含有大量冗余属性，约简结果中只有3个属性，算法只需迭代3次，而chess却需要迭代31次；②mushroom的约简结果是 ｛a5，a20，a3｝ （a5表示第5个条件属性），a5的正域基数为2868，所以在下一次迭代中只需考虑2776个对象，a20的正域基数为2664，所以在下一次迭代中只需考虑112个对象，这样一来，计算时间大大降低了。所以改进的算法在mushroom数据集上运行效率最高。由此说明，改进算法要优于原算法。

表7 约简结果对比图 （属性个数）

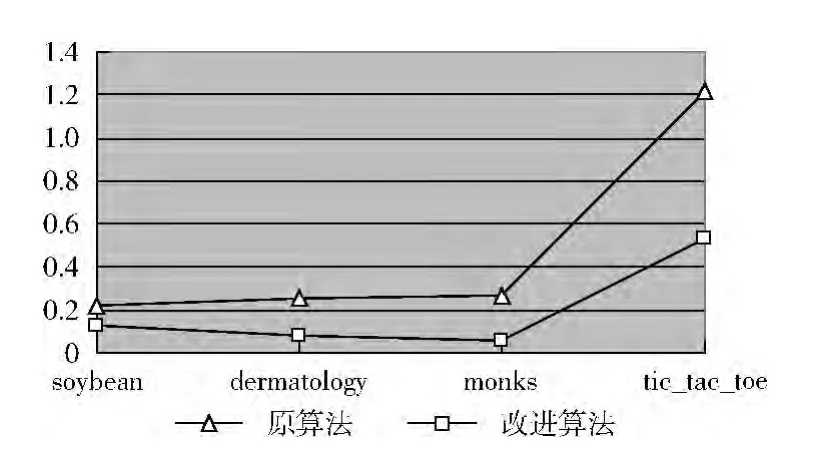
图1 算法运行时间对比1（单位：秒）

图2 算法运行时间对比2（单位：秒）

4 结束语

本文针对大多数属性约简算法运行效率不高的问题，提出了一种基于决策表分解的属性约简算法。此算法通过不断对决策表进行分解，避免了许多重复计算，降低了计算时间。结合正域基数和互信息增益能更客观地衡量属性的重要性。对算法进行了时间复杂度分析，并通过实验对算法的效率进行了测试。实验结果表明，该算法运行效率要优于文献 ［5］中的算法。当数据集越大且含有较多冗余属性时，提高的幅度越明显。今后的工作集中在以下几个方面：对连续型数据属性约简的研究，对不相容决策表的约简研究，以及将约简结果用于分类中。

［1］Pawlak Z.Rough sets ［J］.International Journal of Computer and Information Sciences，1982，11 （5）：341－356

［2］MIAO Duoqian，LI Daoguo.Rough set theory，algorithm and application ［M］.Beijing：Tsinghua University Press，2008（in Chinese）.［苗夺谦，李道国.粗糙集理论﹑算法与应用［M］.北京：清华大学出版社，2008.］

［3］WANG Hui，WANG Jing，ZHANG Caiyun.Improvement of attribute reduction algorithm based on distinction matrix ［J］.Journal of Wuhan University of Science and Technology，2011，34 （2）：126－130 （in Chinese）.［王慧，王京，张彩云.基于区分矩阵的属性约简算法改进策略 ［J］.武汉科技大学学报，2011，34 （2）：126－130.］

［4］WANG Xizhao，WANG Tingting，ZHAI Junhai.An attribute reduction algorithm based on instance selection ［J］.Journal of Computer Research and Development，2012，49 （11）：2305－2310 （in Chinese）.［王熙照，王婷婷，翟俊海.基于样例选取的属性约简算法 ［J］.计算机研究与发展，2012，49 （11）：2305－2310.］

［5］SHEN Wei，ZHAO Jiabao.A new heuristic reduction algorithm of rough sets decision－making table ［J］.Computer Technology and Development，2010，20 （10）：16－20 （in Chinese）.［沈伟，赵佳宝.一种新的启发式粗糙集决策表属性约简算法 ［J］.计算机技术与发展，2010，20 （10）：16－20.］

［6］GE Hao，LI Longshu，YANG Chuanjian.Improvement to quick attribution reduction algorithm ［J］.Journal of Chinese Computer System，2009，30 （2）：308－314 （in Chinese）.［葛浩，李龙澍，杨传健.改进的快速属性约简算法 ［J］.小型微型计算机系统，2009，30 （2）：308－314.］

［7］XUE Shengjun，GUO Qiang.A minimal attribute reduction algorithm ［J］.Journal of Wuhan University of Technology（Transportation Science ＆ Engineering），2012，36 （3）：515－519（in Chinese）.［薛胜军，郭强.一种改进的最小属性约简算法 ［J］.武汉理工大学学报 （交通科学与工程版），2012，36 （3）：515－519.］

［8］JIANG Yu，LIU Yintian，LI Chao.Fast algorithm for computing attribute reduction based on Bucket Sort ［J］.Control and Decision，2011，26 （2）：207－212 （in Chinese）.［蒋瑜，刘胤田，李超，基于Bucket Sort的快速属性约简算法 ［J］.控制与决策，2011，26 （2）：207－212.］

［9］Qian Yuhua，Liang Jiye，Witold Pedrycz.Positive approximation：An accelerator for attribute reduction in rough set theory［J］.Artificial Intelligence，2010，174 （9－10）：597－618.

［10］Qian Yuhua，Witold Pedrycz，Liang JiYe.An efficient accelerator for attribute reduction from incomplete data in rough set frame－work ［J］.Pattern Recognition，2011，44 （8）：1658－1670.

［11］Meng Zuqiang，Shi Zhongzhi.A fast approach to attribute reduction in incomplete decision systems with tolerance relationbased rough sets ［J］.Information Sciences，2009，179（16）：2774－2793.