基于互连网络的比特置换实现技术

常忠祥，戴紫彬，李 伟，陈 帆，马 超

（信息工程大学，河南 郑州450001）

0 引 言

通用微处理器大多以字为单位进行操作，不能很好支持比特置换功能，极大制约了密码算法在处理中的运算性能，因此如何提高比特置换操作在处理器中的执行效率，成为了人们研究的热点。比特置换实现主要有数据选择器、互连网络、基本单元组合3种实现方式，采用数据选择器方式以北京科技大学曲英杰的实现方式为主，可以支持1－1、1－n（n为输入数据位宽）等置换，灵活性强。但存在着资源占用大，配置信息量大，功能冗余等问题，同时，由于其配置信息量大，若采用动态生成的方式，其延时和资源均难以接受，只能采用对配置信息提前配置的方式，不支持动态更换置换种类的功能；采用互连网络实现，以PALMS（princeton architecture laboratory for multimedia and security）的Ruby B.Lee等人提出的PPERM、CROSS、OM－FLIP［1］等指令为主，支持1－1的比特置换，减少了部分冗余功能，但也存在着配置信息量大，只能采用配置信息提前配置的方式，不支持动态更换置换种类；基本单元组合实现主要以通用处理器中移位、异或等基本单元组合为主，可以实现任何一种比特置换操作，但需要的基本单元次数较多，效率较低。

基于此，本文通过分析互连网络的拓扑结构和互连函数，结合归并排序算法的特点，提出了多次通过互连网络的方式实现比特置换，能够动态更换比特置换的种类，有效降低资源的消耗，具有较高的灵活性和处理性能。

1 相关知识

1.1 归并排序算法

归并排序算法［2］可以实现任意序列到固定升序或降序的功能，过程如下：

（1）对输入数据进行两两比较，形成长度为2的多组有序序列；

（2）使用归并的方法 （奇偶归并或双调归并）对2个长度为2的有序序列进行归并，得到长度为4的有序序列；

（3）重复上述步骤，直到所有的数据都归并成一个完整的有序序列为止。

设存在初始序列 ｛7，6，5，4，3，2，1，0｝，目的序列 ｛0，1，2，3，4，5，6，7｝，将序列按照归并排序的算法进行实现，过程如下：

（1）将初始序列进行排序

（7）（6）（5）（4）（3）（2）（1）（0）

（2）归并序列

一次归并：

（6，7）（4，5）（2，3）（0，1）

或

（5，7）（4，6）（1，3）（0，2）

二次归并：

（4，5，6，7）（0，1，2，3）

或

（1，3，5，7）（0，2，4，6）

三次归并：

（0，1，2，3，4，5，6，7）

由归并算法可知，其核心是序列中包含的有序序列个数，与位置无关，其中有序序列在归并时，任何两组序列都可以组合归并，最后形成升序或降序序列。

归并排序强调原始序列中每2个数的比较和条件交换，互连网络的互连特点与归并排序的原理相符，是实现归并排序的良好载体。由归并排序算法可知，实现归并排序，需要一个支持如图1所示的功能模块。

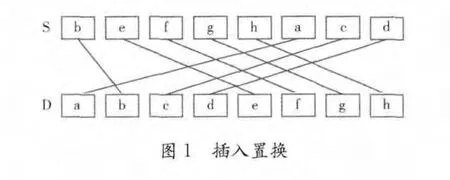
设 （b，e，f，g，h）为一组升序， （a，c，d）为一组升序，通过图1，可以将 （b，e，f，g，h，a，c，d）变换为升序序列 （a，b，c，d，e，f，g，h），即通过图1所示的功能，可以将具有K （0＜K≤N，K，N为正整数，N为源序列中数据的个数）组升序的源序列变换为具有K／2组升序序列的目的序列。

1.2 互连网络的选择

动态阻塞网络主要有STARAN网络、Butterfly网络、Ω网络、数据变换网络、榕树网络、Delta网络、基准网络［2，4－6］等。数据变换网络和榕树网络支持数据的重复、收缩、扩展等置换，若实现输入与输出位宽相同的排序，会造成功能的冗余，从而导致资源的浪费。iButterfly网络、Butterfly网络、Ω网络、简化数据变换网络、逆基准网络和基准网络是实现输入数据与输出数据一一对应的排序的较好选择，且以上几种网络都是拓扑等价的，由于iButterfly网络、Butterfly网络可拆分性强，互连函数简单，可以同时实现多组小位宽的排序，iButterfly、Butterfly网络具有较高的研究价值。

8－8Butterfly网络如图2所示。

对Butterfly网络研究发现，Butterfly网络支持左、右插入置换，与归并排序算法具有很强的相似性，如图3（a）所示，设控制序列C中1的个数为sum，将源数据序列S中最右侧相邻sum比特数据，按顺序填充到1对应的位置，其余数据按照相反顺序填充到0对应的位置；图3（b）与图3（a）相似，只是方向相反，其中采用控制序列C生成网络路由信息的算法及其高速实现在参考文献中已经有具体的方法［7－10］。

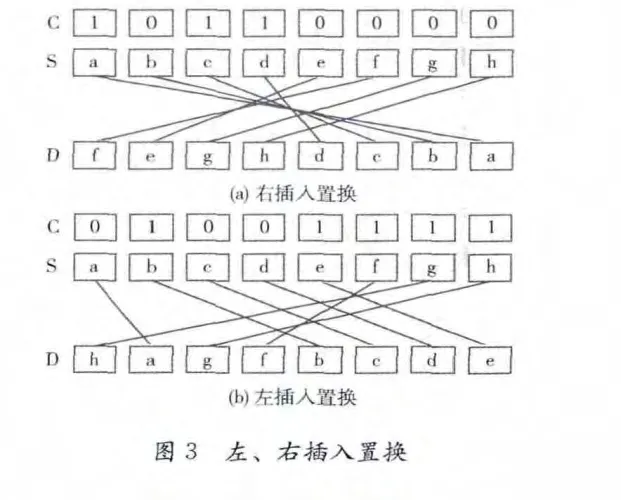
由图3可知，将左、右插入置换的结果进行简单的处理就可以得到图1所示的插入置换，支持归并排序算法，但归并排序算法主要用于将无序的源序列排列成有序序列，而比特置换是将有序的源序列变换为任意的无序序列，即归并排序的逆过程，iButterfly网络与Butterfly网络互逆，对iButterfly网络研究发现，iButterfly网络支持与插入置换互逆的左、右抽取置换，如图4所示。

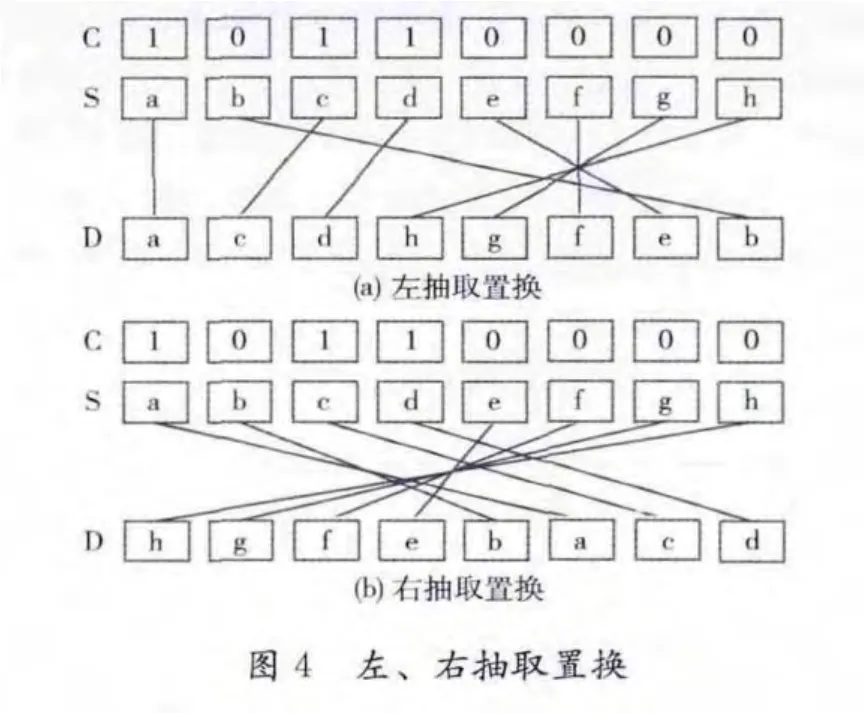
抽取置换与插入置换为互逆的过程，即抽取置换可以还原插入置换的结果，因此，拟以插入置换实现排序为基础，对抽取置换实现比特置换进行研究。

2 基于互连网络比特置换实现

2.1 左、右抽取置换实现比特置换

如图3（a）、图3（b）所示，Butterfly网络支持插入置换和右插入置换，且多次通过单独的左、右插入置换也可以实现排序，因此对采用左插入置换、右插入置换单独实现排序进行了研究。首先分析采用右插入置换 （图3（a））的方法实现排序的方法。

定义1 存在无序序列N，若目的序列为升序序列，则从输入数据的最右端开始，每出现一次升序，记1，则N中存在升序序列个数为num （N）＝M，1≤M≤N；若为目的序列为降序，则按照升序的统计方法，统计序列中的降序，记num （N）＝M，1≤M≤N。

由定义1和图3可知，需要进行M－1次插入置换，当数据进行第u（u＞1）次插入置换时，前面已经定位好的数据，很有可能被本次数据定位打乱，形成新的序列，可以发现，采用右插入置换的方法，需要对初始的无关数据清零，即将图3（a）中，C序列和S序列相与。将处理后的数据进行右插入置换操作，最后将插入后的数据相或，即可得到排序结果。

同理，采用抽取置换实现比特置换与插入置换实现排序的过程相同，需要进行M－1次抽取置换和logN2次或操作即可以实现比特置换。对抽取置换进行深入分析，可以发现，当数据进行第u（u＞1）次抽取置换时，只需要将已经抽取好的数据对应的控制信息填充为1，不会打乱已经排好的顺序，可以很好的避免或操作，基于此，提出了另一种比特置换实现方式。

定义2 存在无序序列N，若目的序列为升序序列，则从输入数据的最右端开始，每出现一次升序，记1，剩余数据反序，然后统计新序列中的右端升序，则N中存在升序序列个数为num （N）＝M，1≤M≤N；若为目的序列为降序，则按照升序的统计方法，统计序列中的降序，记num （N）＝M，1≤M≤N。

抽取实现比特置换见表1。

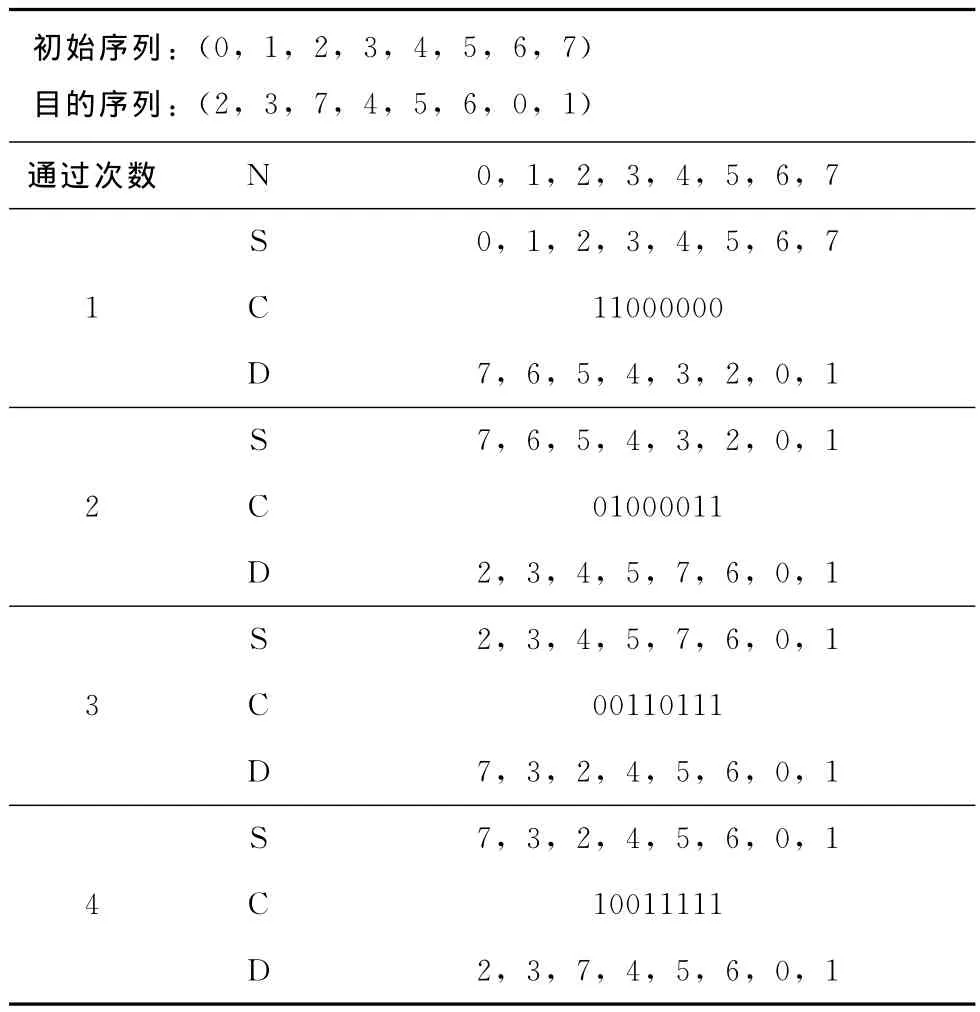
表1 抽取实现比特置换

此类实现方法不仅需要左、右抽取置换，还需要异或操作，虽然能够减少通用处理器中比特置换实现所需的指令条数，但需要消耗大量的存储资源，且操作复杂。对于num （N）≤2的混乱序列，只需要一次通过即可实现，该类序列一共有2N种。对于num （N）＞2的混乱序列，该类方法并不能很好的满足比特置换的需求。因此，结合归并排序算法，对左、右抽取置换实现比特置换的方式进行了改进。

2.2 改进抽取置换实现比特置换

归并排序主要通过减少初始乱序中的有序序列个数来实现排序算法，图1所示的插入置换功能才能更好的满足排序算法，对左、右插入置换分析发现，将左、右插入置换的初始序列中无关数据清0，然后进行插入置换，将两者结果相或，可得到图1的结果，因此，研究在排序和比特置换过程中，控制序列C的生成方式。

定义3 存在无序序列N，若目的序列为升序序列，则从输入数据的最左端开始，每出现一次升序，加1，则N中存在升序序列个数为num （N）＝M，1≤M≤N；若为目的序列为降序，则按照升序的统计方法，统计序列中的降序，记num （N）＝M，1≤M≤N。

事实1：存在序列N的num （N）＝M，则存在序列T，num （T）＝｜｜，通过改进的数据定位功能，使得序列N变换为序列T。

结合归并算法和改进的插入置换，提出了控制序列C生成算法。

N1，N2，N3，…，Nm表是前｜｜个序列，｜｜表示上取整，sort表示升序排列。

改进的插入置换实现排序 （以8比特为例）见表2。

表2 改进的插入置换实现排序 （以8比特为例）

左、右抽取置换进行处理，可以得到该进的左、右抽取置换，如图5所示。

改进的插入置换和改进的抽取置换互为逆过程，因此，若从固定序列到任意序列的比特置换操作，只需将插入过程反序，将插入的源序列作为抽取的目的序列，控制信息生成方式相同。见表3。

表3 抽取置换实现比特置换

2.3 改进插入、抽取置换硬件架构

通过以上分析，提出了改进后的插入置换硬件架构和改进后的抽取置换硬件架构。

如图6、图7所示，改进插入置换硬件架构主要包括路由信息生成电路，Butterfly网络和前后处理电路。改进抽取置换硬件架构主要包括路由信息生成电路，iButterfly网络和前后处理电路。

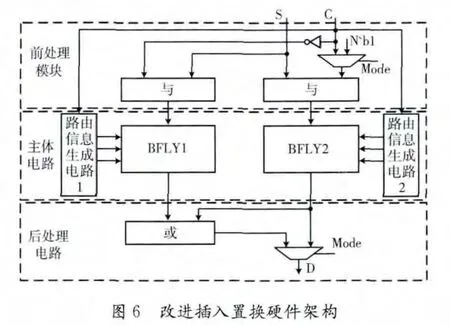
前处理电路为2个与门和一个非门，将初始输入数据S与控制信息C、～C或N比特1相与，当输入数据num（N）≤2时，Mode选择N比特1与S相与。当num （N）＞2时，Mode选择C、～C与S相与，将S中对应C和～C中对应0位置的数据清0后参与插入、抽取置换，两架构前处理模块相同。

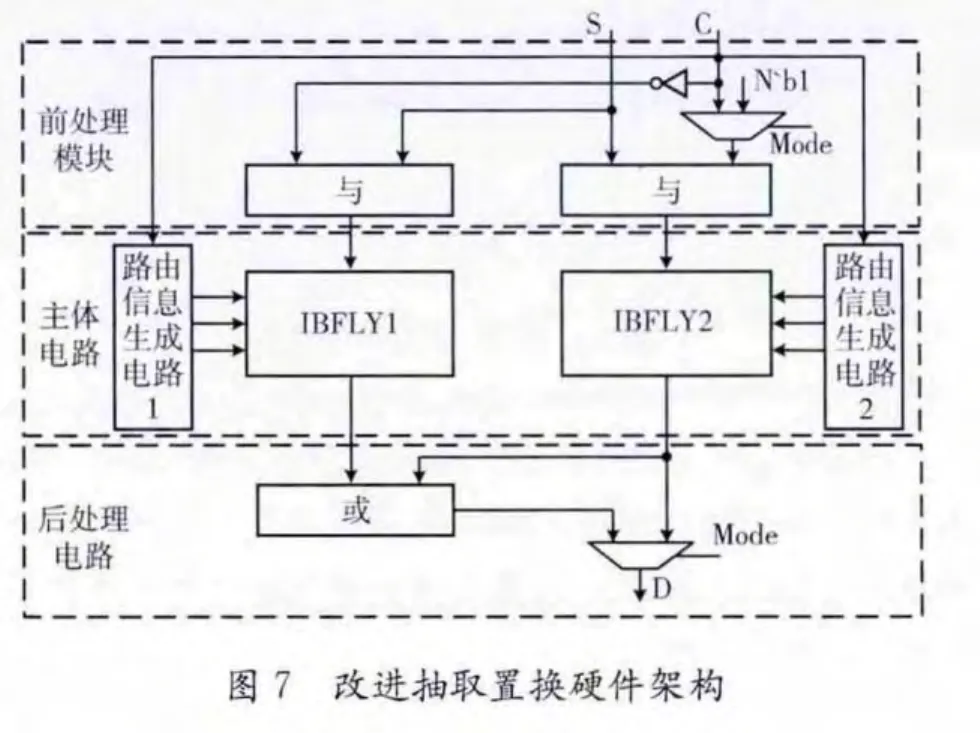
路由信息生成电路和互连网络为架构的核心，图6中路由信息1和BFLY1，负责左插入置换，路由信息2和BFLY2，负责将右插入置换；图7中路由信息1和IBFLY1，负责左抽取置换，路由信息2和IBFLY2，负责将右抽取置换；路由信息生成算法相同，仅控制方式和主体电路不同。

后处理电路选择要输出的结果，针对插入置换，当输入数据num （N）＞2时，Mode选择BFLY1和BFLY2相或得结果输出。当num （N）≤2时，Mode选择BFLY2结果输出。对于抽取置换，当输入数据num （N）＞2时，Mode选择IBFLY1和IBFLY2相或结果输出。当num （N）≤2时，Mode选择IBFLY2结果输出。

3 功能验证和性能评估

为了保证本文提出的置换硬件架构的功能和性能，本文对硬件架构进行了编码实现和逻辑综合。

如表4所示，在CMOS 180nm下，分别对位宽为32bit、64bit、128bit插入置换的架构进行评估，由评估结果可知，当位宽较小时，其消耗的资源和关键路径会急剧减小。

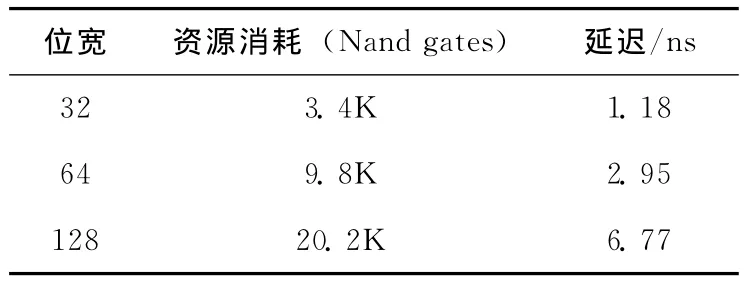
表4 架构性能分析

表5 为以64bit为基本的处理单元实现DES算法中的比特置换，采用改进的抽取置换实现比特置换，可以有效地降低处理器中比特置换需要的指令条数，且灵活性较强。若采用小位宽的比特置换实现大位宽的比特置换，只需将数据利用移位和与操作进行分组，分组后的数据再比特置换即可。

表5 DES中比特置换适配

4 结束语

本文结合比特置换操作特点、归并排序算法、互连网络拓扑结构和互连函数等的特点，提出了多次通过互连网络实现比特置换的方法，提出了专门的控制序列生成算法，结合已有的路由信息生成算法，由控制序列实时生成网络路由信息。结果表明，该方法便于硬件实现，且能够通过较少的次数完成比特置换操作，有效的缓和比特置换实现时资源与速度的矛盾。

随着比特置换处理位宽的增大，本文提出架构的关键路径和资源消耗会急剧增加，下一步需要对提出架构的硬件实现方式进行优化，降低关键路径的长度，同时对小位宽置换实现大位宽置换进行深入研究。

［1］Hilewitz Yedidya.Advance bit manipulation instructions：Architecture，implementation and applications ［D］.NewJersey：Princeton University，2008.

［2］Yedidya Hilewitz，Ruby B Lee.A new basis for shifters in general－purpose processors for existing and advanced bit manipulations［J］.IEEE Transactions on Computers，2009，58（8）：1035－1048.

［3］AzariaPaz.A theory of decomposition into prime factors of layered interconnection networks ［J］.Discrete Applied Mathematics，2011，159 （7）：628－646.

［4］John Garofalakis，Eleftherios Stergiou.An analytical model for the performance evaluation of multistage interconnection networks with two class priorities ［J］.Future Generation Computer Systems，2013，29 （1）：114－129.

［5］George R Exner.Aluthge transforms and n－contractively of weighted shifts ［J］.Journal of Operator Theory，2009，61（2）：419－438.

［6］Kurian AP，Puthusserypady S.Self－synchronizing chaotic stream ciphers［J］.Signal Processing，2008，88 （10）：2442－2452.

［7］XU Jianbo，DAI Zibin.Reconfigurable design on extract and insert unit of stream cipher ［J］.Electronic Technology Applications，2011 （7）：65－67 （in Chinese）.［徐建博，戴紫彬.面向序列密码抽取与插入单元可重构设计研究 ［J］.电子技术应用，2011 （7）：65－67.］

［8］David Arroyo.Cryptanalysis of a one round chaos－based substitution permutation network ［J］.Signal Processing，2013，93（5）：1358－1364.

［9］Chang PeiChann，WeiHsiuHuang.A block mining and recombination enhanced genetic algorithm for the permutation flow shop scheduling problem ［J］.Int J Production Economics，2013，141 （1）：45－55.

［10］Sun G，Wu C.The lower bounds on the second order nonlinearity of three classes of Boolean functions with high nonlinearity ［J］.Inform Sci，2009，179 （3）：267－278.