基于primal RankRLS方法的本体映射算法*

兰美辉， 徐坚， 高炜

(1.曲靖师范学院 计算机科学与工程学院，云南 曲靖 655011;2.云南师范大学 信息学院，云南 昆明 650092)

1 引 言

作为一种表示、存储和管理信息的工具，本体被广泛应用于生物制药[1]、教育科学[2]等各个领域.本体映射的本质是寻找不同本体间相似程度大的概念，从而在不同的本体间建立联系[3].近年来,排序学习算法被广泛应用于本体映射，其本质是得到排序函数，通过该函数将实例映射成实数，再通过比较实数间的差值来判定两概念的相似程度.相关内容可参考文献[4-9].

设图G1、G2、…、Gk分别对应本体O1、O2、…、Ok，令G=G1+G2+…+Gk.本文利用primal RankRLS算法得到本体映射算法.文章的结构组织如下：首先简单介绍RankRLS算法[10]；其次，在第三节中针对多本体图的结构特征将primal RankRLS算法融入本体概念相似度计算，进而得到本体映射；最后，通过一个具体实验验证新算法的有效性.

2 RankRLS简介

设X为输入空间.排序函数f：X→可以看成一个得分函数，它将X中每个数据映射成一个实数，数据之间的排名通过比较实数间的大小来确定，实数值越大，排名越高.排序学习算法的目标即是找到最优的排序函数.

设RX为从输入空间X到实数R的所有函数的集合.H⊆RX为假设空间(即排序函数f∈H).对任意映射Φ：X→F，内积k(x,x')≤Φ(x)、Φ(x')称为核函数，其中x、x'∈X.n×n对称核矩阵K如下：

由输入空间X和核函数k:X×X→决定的再生核希尔伯特空间(RKHS)记为Hk,X.RankRLS算法A可形式化表示为

(1)

其中

(2)

λ表示正则化常数,c(f(S),G)为代价函数.根据表示理论，使(1)达到最小的f∈Hk,X可表示为

(3)

这里ai∈R.令

(4)

其中实值参数wi、zi>0.则

(5)

设A∈Rn是最小化(5)的解，则

A=(MMTK+λI)-1MN

(6)

3 新算法描述

对于单本体图的概念相似度计算，将RankRLS算法融入本体映射算法，由于zi一般取与边标记yi相关的数(例如：直接取zi=yi)，因此只需根据本体自身的结构设计边权值函数w即可.但在多本体映射中，还需处理另外一个问题，即在多本体图中，顶点的数量会非常庞大，此时选取样本点的数量也会非常大，远远超过数据本身的维数，导致算法的计算量会非常大.因此，需要将学习理论中降维的思想运用于排序学习算法.具体的做法是运用改进的RankRLS算法-primal RankRLS算法融入本体相似度计算.

3.1 运用primal RankRLS算法

对于样本S=(x1,…,xn)，取特征空间为Rl.令矩阵

H=(Φ(x1),…,Φ(xn)).

则最优化(1)得到的函数(3)的具体形式可表示为

f(x)= Φ(x)THA=Φ(x)TW，

这里，W=HA表示RankRLS算法在特征空间的解所对应的超平面的赋范向量，其维数等于特征空间的维数l，而与n无关；A是式(3)中由ai∈R决定的向量.此类方法称为primal RankRLS, 它能大大降低计算复杂度，使其由特征空间的维数l决定，而与n无关.

式(1)可写为

这里，J(W,G)=(N-MTHTW)T(N-MTHTW)+λWTW.

对J(W,G)关于W求导可得：

令导数的值为0，则可得关于W的解为：

W=(HMMTHT+λI)-1HMN.

(7)

该解对应原来RankRLS算法的解(6).

通过解最优化模型(6)得到排序函数f.对任意v∈V(Gi)，其中1≤i≤k.选择阈值M，返回集合{u∈V(G-Gi)，|f(u)-f(v)|≤M}作为顶点v的映射.

4 实 验

实验构建了两个“Computer”本体O1、O2,其结构如图1、图2所示.采用P@N[11]准确率来评价实验，对实验结果进行分析，P@1平均准确率达62.50%，P@3平均准确率达70.83%，P@5平均准确率达79.17%，所以该算法是有效的.

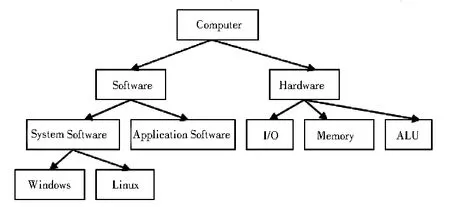
图1 “Computer”本体O1结构图

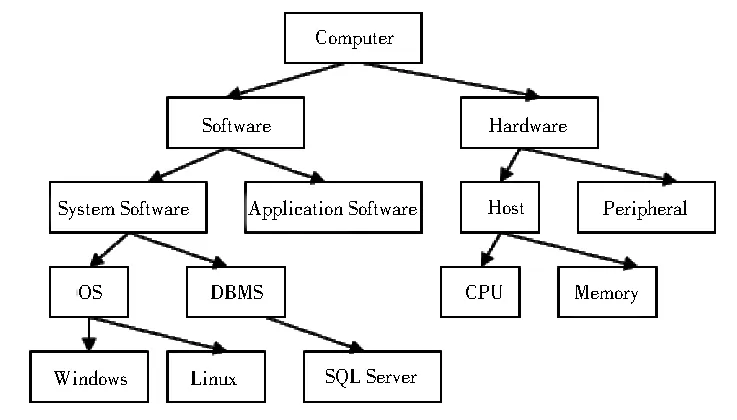
图2 “Computer”本体O2结构图

5 结束语

本文运用primal RankRLS学习算法对所有多本体图的所有顶点给出了一个序列，并根据两概念对应顶点对应实数的差值来判断它们的相似程度，由此得到本体映射.算法适用于多本体图顶点数量庞大的情况，支持大规模运算，具有广阔的应用前景.

参 考 文 献:

[1] HE X,WANG Y,GAO W.Ontology similarity measure algorithm based on KPCA and application in biology science[J].Journal of Chemical and Pharmaceutical Research，2013,5(12):196-200.

[2] BOUZEGHOUB A,ELBYED A.Ontology mapping for web-based educational systems interoperability[J].Interoperability in Business Information Systems,2006,1(1):73-84.

[3] SU X,GULLA J A.Semantic enrichment for ontology mapping[C].Natural Language Processing and Information Systems:9th International Conference on Applications of Natural Languages to Information Systems,Salford,UK,2004,Proceedings.Springer,2006,3136:217-228.

[4] JOACHIMS T.Optimizing search engines using clickthrough data[C].Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining,Washington,DC,USA,2002,133-142.

[5] CHUA T S,NEO S Y,GOH H K.Trecvid 2005 by nus pris[R].NIST TRECVID,2005.

[6] CORTES C,MOHRI M,RASTOGI A.Magnitude-preserving ranking algorithms[C].Proceedings of the 24th International Conference on Machine Learning,Corvallis,USA,2007,169-176.

[7] COSSOCK D,ZHANG T.Subset Ranking Using Regression[C].Proceedings of the 19th annual conference on Learning Theory,Pittsburgh,USA,2006,Springer-Verlag,2006,605-619.

[8] YAN R,HAUPTMANN A G.Efficient margin-based rank learning algorithms for information retrieval[C].Image and Video Retrieval:5th International Conference,Tempe,USA,2006,Proceedings Springer,2006,4071,113-122.

[9] RUDIN C.Ranking with a P-Norm Push[C].Proceedings of the 19th annual conference on Learning Theory,Pittsburgh,USA,2006,Springer-Verlag,2006,589-604.

[10]PAHIKKALA T,TSIVTSIVADZE E,AIROLA A, et al.An efficient algorithm for learning to rank from preference graphs[J].Mach Learn,2009,75(1):129-165.

[11]CRASWELL N,HAWKING D.Overview of the TREC 2003 web track[C].Proceedings of the 12th Text Retrieval Conference,Gaithersburg,USA,2003,NIST Special Publication,2003:78-92.