TC4钛合金试样渐进破坏试验与数值研究

刘 超， 孙 秦， 刘彦杰

(西北工业大学 航空学院，西安710072)

金属材料的单向拉伸试验为研究材料基本力学性能提供了数据参考。模拟金属棒材试件在单向拉伸状态下的裂纹形成与扩展直至完全断裂的全过程非常必要。数值仿真与真实试验相比成本低，并能获得真实试验难以测量的数据。因此，基于断裂力学或损伤力学为基本理论进行数值模拟延性金属构件的断裂过程一直是工程材料力学性能研究中的热点。在对光滑圆试样和带缺口试样的有限元仿真计算中，通常选用含旋转的轴对称单元(二维单元)来划分网格，将本应选用体单元划分网格进行分析的三维应力问题进行简化。三维应力状态下的数值计算更接近于试件单向拉伸直至断裂的整个过程。

杨庆生等［1］基于自适应有限元法的基本原理并假设裂纹沿着单元之间的路径连续扩展，发展了一种可随裂尖连续移动的网格动态加密和释放方法。黄向平等［2］讨论了自适应有限元模拟裂纹扩展的网格生成技术，通过修改裂纹周围单元的形状及单元间的邻接关系，实现网格动态划分对裂纹扩展的跟踪。上述研究均基于断裂力学基本理论并用有限元法进行数值分析，其局限性为必须确定裂纹扩展的路径或不断地重新划分网格。文献［3 ～5］分别利用边界元方法、热权函数法和多虚拟裂纹扩展技术、有限元法研究了三维状态下I 型裂纹扩展。然而其局限性为均采用断裂力学方法研究，所选构件必须含有初始裂纹，无法模拟无初始裂纹构件的裂纹萌生。文献［6］在总结前人［7，8］研究的基础上提出了Gurson 模型，Tvergaard 和Needleman［9～12］随后对初始Gurson 模型进行了修正。应用GTN 本构模型能够模拟通过空穴形核和长大的累积微观断裂，因此可以应用于模拟金属的延性断裂。

TC4 钛合金以其强度高、耐蚀性好、耐热性高的特点广泛应用于航空航天工业中，主要用于制造发动机的风扇和压气机盘及叶片以及飞机结构中的梁和隔框等重要承力构件。但人们通常关注合金的制备工艺对性能影响的研究，最近赵嘉琪等［13］研究了α 污染层对铸态合金冲击性能的影响，刘晓华等［14］研究了焊接接头的疲劳性能，但是少有关于合金受力过程的报道。本工作采用GTN准则与有限元数值计算相结合的方法对TC4 钛合金光滑圆试样和两种不同缺口形式的试样进行静力破坏过程的数值模拟。模拟时除了选用含旋转的轴对称单元(二维单元)来划分网格的简化计算外，又采用三维应力状态下体单元划分网格的方法来模拟TC4 钛合金棒材试件单向拉伸试验的过程。并与试验结果进行了对比分析。

1 TC4 钛合金静强度单向拉伸试验

1.1 TC4 钛合金光滑圆试样和带缺口试样的静力拉伸试验

单向拉伸试验所选材料为高强度变形TC4 钛合金，其名义化学成分如表1 所示［15］。

三种试样的TC4 钛合金单向拉伸试验分别为:光滑圆试样的单向拉伸试验(图1a 定义为试样a)，两种带有不同大小缺口试样的单向拉伸试验(图1b和图1c，定义为试样b 和试样c)。三种形状试样拉伸试验均在Instron8801 试验机上进行，试样尺寸如图1 所示。三种形状试样断裂后的宏观形貌如图2所示。TC4 钛合金工程应力-应变曲线和真实应力-应变曲线如图3 所示。其中真实应力-应变曲线中未包含颈缩后的无效数据，因为利用颈缩前的数据就能完成基体无损伤真实应力-应变曲线的构造。

表1 TC4 钛合金的化学成分(质量分数/%)Table 1 Chemical compositions of TC4 titanium alloy(mass fraction/%)

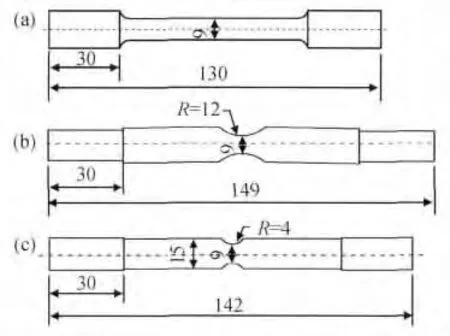
图1 试样示意图Fig.1 Illustration of specimens (unit:mm) (a)specimen a;(b)specimen b;(c)specimen c

图2 3 种拉伸试样宏观断裂形貌Fig.2 Macroscopic fracture morphology of three specimens(a)specimen a;(b)specimen b;(c)specimen c

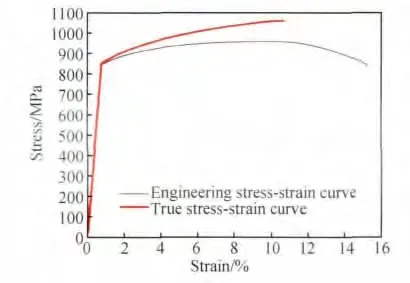
图3 应力-应变曲线Fig.3 Stress-strain curve

2 损伤模型和本构关系

2.1 GTN 模型

Gurson 模型中考虑了静水压力和空穴体积分数对屈服面的影响。材料的空穴体积分数f 是一个从0 到1 的数，分别对应无损伤材料和完全损伤材料。Tvergaard 和Needleman 随后对Gurson 模型进行修正，其表达式如下:

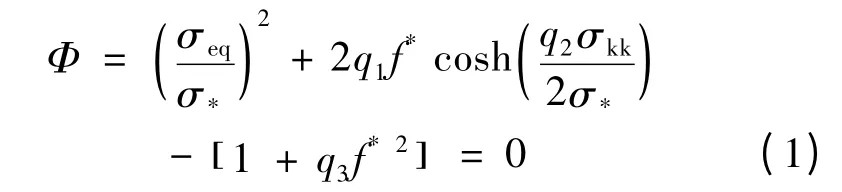
式(1)中σeq为Von-Mises 等效应力，σ*为基体的流变应力，σkk为第一应力不变量，q1，q2，q3为考虑到空穴周围非均匀应力场和相邻空穴之间相互作用的修正系数，且q3=q21。f*为材料空穴体积分数的方程，如式(2)和式(3):

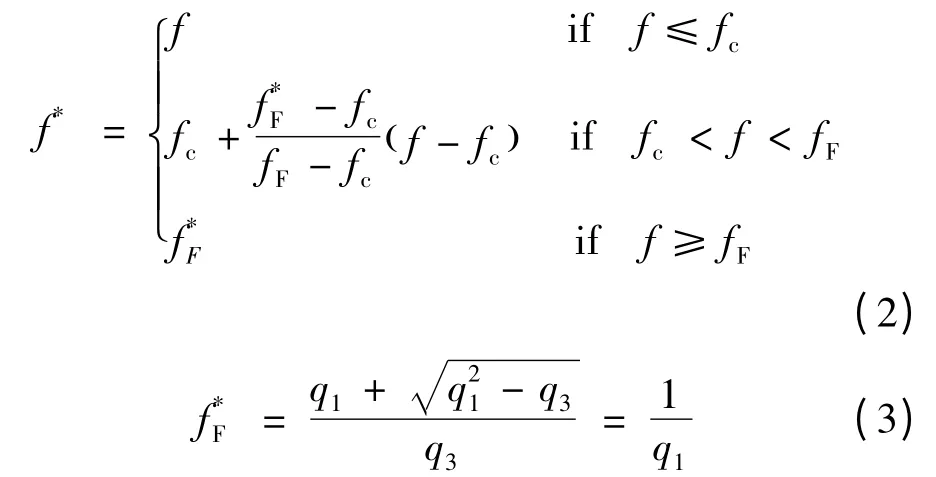
式(2)中fc表示空穴体积分数的临界值，当f 达到fc时材料的应力承载能力便迅速衰减。fF表示应力承载能力完全丧失时的空穴体积分数。f*F为关于q1，q2，q3的方程。空穴的形成情况可用下式表示:

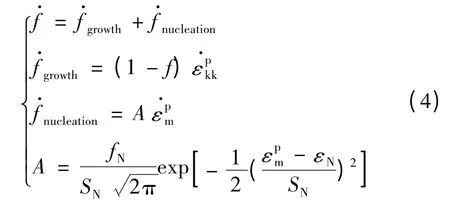
2.2 金属大变形的本构关系

由正交性条件和塑性加载的一致性条件，张克实［16］给出了适用于金属大变形的GTN 塑性本构方程如下:

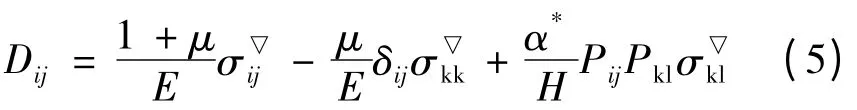
式(5)的逆行式如式(6)所示:

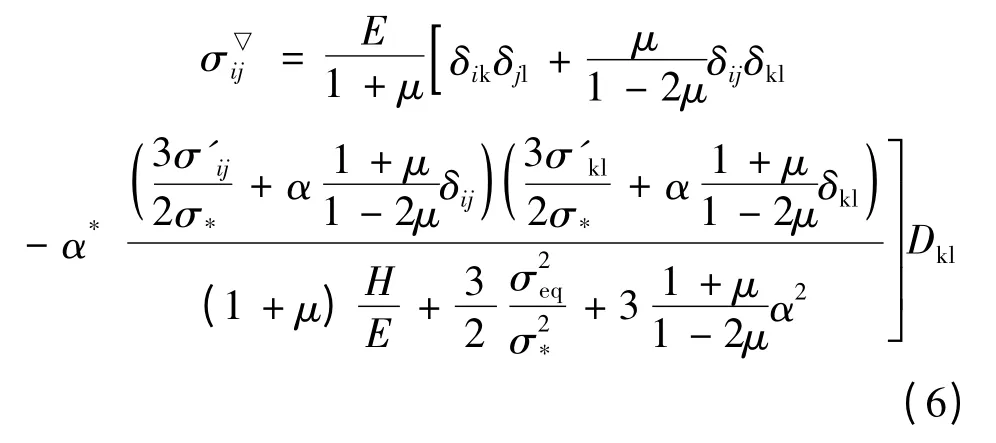
式(5)和式(6)中

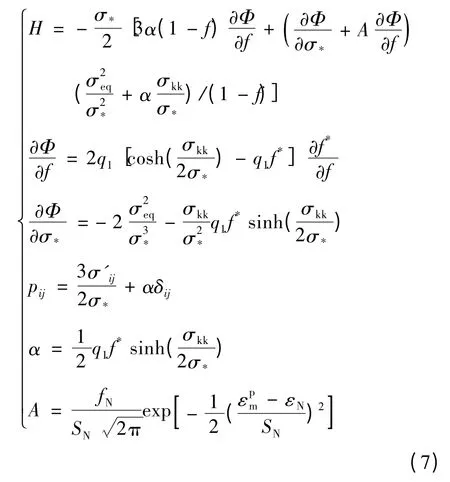
Dij是形变率张量且vi是物质点的速度，xi是瞬时坐标;σ▽ij是柯西应力σij的Jaumann 率;E，μ 为弹性模量和泊松比;σ'ij为应力偏张量;α*在单向拉伸时取值为1;δij是克罗内克符号;σeq为Von-Mises 等效应力;σ*为基体的流变应力;Φ 为式(1)所表示的空穴材料的塑性势。

3 三种试样单向拉伸的数值计算

3.1 光滑圆试样、带缺口试样单向拉伸试验的数值仿真计算

三维有限元模型根据光滑圆试样和两种不同缺口半径的试样全尺寸建模，二维有限元模型选取横截面的1/2 且沿长度方向的纵轴为对称轴，如图4和图5 所示，在长度方向(y 方向)一端施加位移约束，另一端添加位移载荷，后处理中可通过计算约束端支反力的方式确定力载荷。划分网格时两端稀疏，预计断裂的危险区域加密网格。

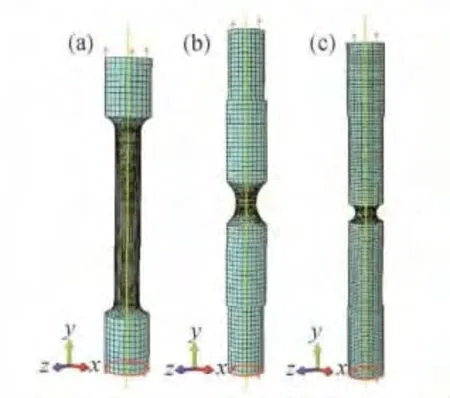
图4 三维有限元模型图Fig.4 Illustration of the 3-dimensional finite element model(a)specimen a;(b)specimen b;(c)specimen c

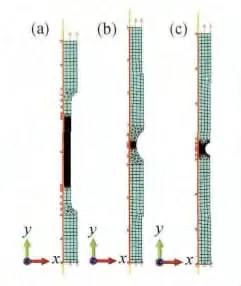
图5 二维有限元模型图Fig.5 Illustration of the 2-dimensional finite element model(a)specimen a;(b)specimen b;(c)specimen c

三维有限元模型中单元类型采用带有沙漏控制的8 节点缩减积分体单元(C3D8R)。在稀疏区与加密区之间用四面体单元(C3D4)过渡。二维有限元模型中单元类型采用沙漏控制的4节点缩减积分轴对称单元(CAX4R)。稀疏区与加密区之间用轴对称单元(CAX3)进行过渡。加密区最小单元尺寸取0.1mm。数值计算中所选材料密度ρ =4400kg/m3，泊松比μ =0. 34，弹性模量E =1.09 ×105MPa 可由弹性段试验数据获得。应用GTN 损伤模型进行数值计算需要的无损伤材料的应力-应变曲线获取方法可通过材料真实应力-应变曲线进行适当处理得出［17］，材料弹性数据保持不变，进入塑性后在曲线上远离真实应力最大值的某一点处将其延伸，并选择延伸起点应变为0.025，如图6 所示。

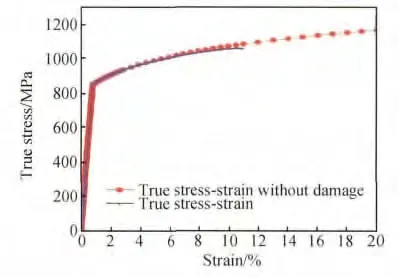
图6 真实应力-应变曲线Fig.6 True stress-strain curve

将图6 中的真实应力-应变曲线应用式(8)进行处理，即可得到材料进入塑性后无损伤的真实应力-塑性应变曲线，如图7 所示。

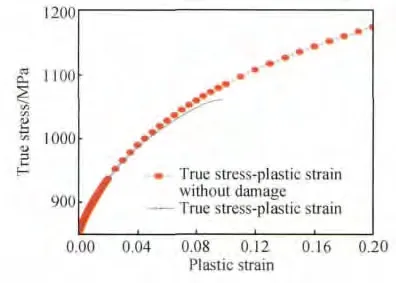
图7 真实应力-塑性应变曲线Fig.7 True stress-plastic strain curve

图7 中所示无损伤情况下真实应力-塑性应变曲线即为数值计算所需要输入的塑性数据，可表示为式(9)的形式。

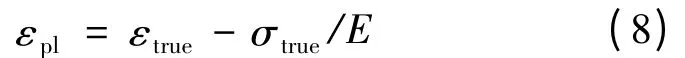
式(8)中εpl表示塑性应变，εtrue表示真实应变，E 为弹性模量，σtrue为真实应力。

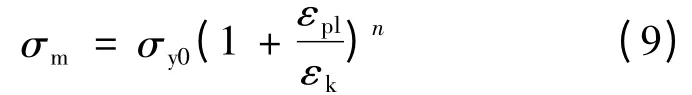
式(9)中εpl表示塑性应变，εk表示参考应变，σy0初始屈服应力，σm为无损伤曲线中硬化阶段的真实应力，n 为硬化指数。计算中所选无损伤真实应力-塑性应变曲线参数为σy0=850MPa，εk=0.018，n =0.13。

数值计算中对于绝大多数金属材料而言选用q1= 1.5 ，q2= 1 ，q3= 2.25 ，fN是一个小于1 的数，通常取值范围在(0.01，0.07)之间，εN取值范围在(0.1，0.3)，SN取值范围在(0.05，0.1)，空穴体积分数的初值f0= 0 ，即假设材料初始状态是完全无任何损伤的。fc和fF可根据试样断裂发生时载荷-位移曲线中的数据确定。且fc和fF相比，断裂发生时关键空穴体积分数fc起决定作用。通过数十次有限元数值计算，并与真实试验所得载荷-位移曲线进行反复对比，并使最大误差小于5%，最终确定的GTN 损伤模型参数如表2 所示。

表2 数值仿真选用的GTN 损伤模型参数Table 2 GTN damage model parameters for simulation

应用上述GTN 模型参数分别对本工作所选三种单向拉伸试样进行数值计算后，三维应力状态下有限元计算所得载荷-位移曲线相对应的预测宏观断裂形貌与试验结果对比，如图8 所示。

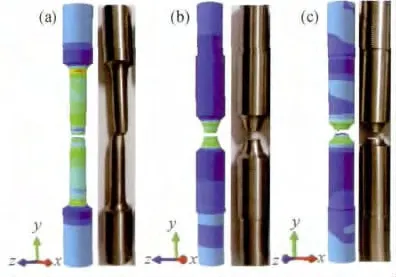
图8 对比各试样宏观断裂形貌的试验结果和仿真结果Fig.8 Comparison of macroscopic fracture morphology of three specimens between experimental and simulation results(a)specimen a;(b)specimen b;(c)specimen c

通过图8 对比各试样宏观断裂形貌的试验结果和仿真结果可知，GTN 模型预测出的三种试样的宏观断裂形貌，与真实试样宏观断裂形貌基本一致。仿真结果和光滑圆试样拉断后的断面收缩情况，均能反映出光滑圆试样在拉伸过程中出现过明显的颈缩现象。所得各试样载荷-位移曲线与数值仿真所得载荷-位移曲线如图9 所示。

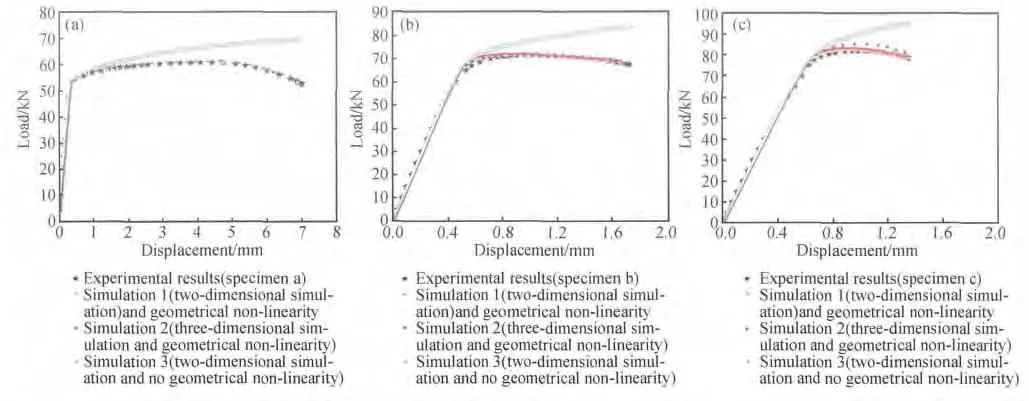
图9 试验数据和仿真结果的载荷-位移曲线Fig.9 Comparisons of load-displacement curves between experimental and simulation results(a)specimen a;(b)specimen b;(c)specimen c

由图9 可知，应用GTN 模型在考虑几何非线性［18］时可以很好地预测出TC4 光滑圆试样和两种带有不同尺寸缺口的试样的载荷-位移曲线，清晰地反映了三种试样在单向拉伸直至断裂的整个过程。二维有限元模型计算结果与三维有限元模型计算结果略有偏差，但与真实试验载荷-位移曲线结果相比误差均小于5%。当不考虑几何非线性的影响时所得结果在弹性段相差不大，但是在塑性大变形阶段，载荷-位移曲线明显比考虑几何非线性时显得“刚硬”的多，即在塑性变形阶段相同位移条件下的载荷要明显大于考虑几何非线性作用的结果。因此，从数值模拟结果验证了研究延性金属大变形问题时考虑几何非线性作用的必要性。

4 结论

(1)通过二维和三维有限元模型对TC4 光滑圆试样和两种不同缺口尺寸的试样进行建模，利用GTN 模型对三种试样的静强度拉伸试验进行预测。结果表明数值计算所得载荷-位移曲线与真实试验所得结果基本一致，较好地反映了三种试样的静强度渐进破坏过程。

(2)在三维应力状态下使用GTN 模型进行数值计算后预测所得三种试样的TC4 钛合金宏观断裂形貌与真实试验所得结果基本一致。

［1］杨庆生，杨卫.断裂过程的有限元模拟［J］. 计算力学学报，1997，14(4):407 －412.(YANG Q S，YANG W. Finite element simulation of fracture process［J］.Chinese Journal of Computational Mechanics，1997，14(4):407 －412.)

［2］黄向平，王建华.裂纹跟踪的网格生成技术［J］. 上海交通大学学报，2001，35(4):493 －495.(HUANG X P，WANG J H. Mesh generation technique of tracing crack propagation［J］. Journal of Shanghai Jiaotong University，2001，35(4):493 －495.)

［3］邓建刚，薛和洋，黎在良，等. 三维裂纹扩展轨迹的边界元数值模拟［J］. 应用力学学报，2003，20(2):49 －53.(DENG J G，XUE H Y，LI Z L，et al. Boundary element numerical simulation of three-dimensional crack growth trajectory［J］. Chinese Journal of Applied Mechanics，2003，20(2):49 －53. )

［4］卢炎麟，黄鲜萍，姜献峰，等. 三维热权函数法和多虚拟裂纹扩展技术［J］. 计算力学学报，2003，20(3):302 －308.(LU Y L，HUANG X P，JIANG X F，et al. 3-D thermal weight function method and multiple virtual crack extension technique［J］. Chinese Journal of Computational Mechanics，2003，20(3):302 －308. )

［5］DUARTE C A，HAMZEH O N，LISZKA T J，et al.A generalized finite element method for the simulation of three dimensional dynamic crack propagation［J］. Computer Methods in Applied Mechanics and Engineering，2001，190(17):2227 －2262.

［6］GURSON A L. Continuum theory of ductile rupture by void nucleation and growth［J］. Journal of Engineering Materials and Technology，1977，99(1):2 －15.

［7］RICE J R，TRACEY D M. On the ductile enlargement of voids in triaxial stress fields［J］. Journal of the Mechanics and Physics of Solids，1969，17(3):201 －217.

［8］MCCLINTOCK F A. A criterion for ductile fracture by the growth of holes［J］. Journal of the Mechanics，1968，35:363 －371.

［9］TVERGAARD V. Influence of voids on shear instabilities under plane strain conditions［J］. International Journal of Fracture，1981，17 (4):389 －407.

［10］TVERGAARD V. Material failure by void coalescence in localized shear band［J］. International Journal of Solids and Structures，1982，18 (8):659 －672.

［11］TVERGAARD V. On localization in ductile materials containing spherical voids［J］. International Journal of Fracture，1982，18 (4):237 －246.

［12］TVERGAARD V，NEEDLEMAN A. Analysis of the cupcone fracture in a round tensile bar［J］. Acta Metallurgica，1984，32 (1):157 －169.

［13］赵嘉琪，吴国清，程祥军，等. α 污染层对ZTC4 钛合金铸态试样冲击性能的影响［J］. 材料工程，2013(6):59－62.(ZHAO J Q，WU G Q，CHENG X J，et al. Effects of the contamination of a layer on the impact properties of ZTC4 titanium casting sample［J］.Journal of Materials Engineering ，2013(6):59 －62.)

［14］刘晓华，马英杰，李晋炜，等.TC4 钛合金电子束焊接接头低周疲劳性能研究［J］.航空材料学报，2013，33(3):53 －57.(LIU X H，M Y J，LI J W，et al.Low cycle fatigue properties of electron beam welded TC4 titanium alloy［J］. Journal of Aeronautical Materials，2013，33(3):53 －57.)

［15］颜鸣皋，刘伯操，李金桂，等. 中国航空材料手册［M］.北京:中国标准出版社，2002.(YAN M G，LIU B C，LI J G，et al. China Aeronautical Materials Handbook ［M］. Beijing:Chinese Standard Press，2002.)

［16］张克实，李世辉，郑长卿. 裂尖细观断裂研究—大应变情形下应力、变形和空穴演变的分析［J］. 西北工业大学学报，1988，6(4):435-444.(ZHANG K S，LI S H，ZHANG C Q. On micro-fracture of crack tip-analyses of the stress，strain and void development under large deformation conditions［J］. Journal of Northwestern Polytechnical University，1988，6(4):435 －444.)

［17］CUESTA I I，ALEGRE J，LACALLE R. Determination of the Gurson-Tvergaard damage model parameters for simulating small punch tests［J］. Fatigue ＆ Fracture of Engineering Materials ＆ Structures，2010，33:703 －713.

［18］庄茁，由小川，廖剑晖，等. 基于ABAQUS 的有限元分析和应用［M］. 北京:清华大学出版社，2009.(ZHUANG Z，YOU X C，LIAO J H，et al. Finite Element Analysis and Application Based on ABAQUS［M］. Beijing:Tsinghua University Press，2009.)