基于直通型CT试样测试方法的断裂韧度研究

姚 瑶， 蔡力勋， 包 陈， 石凯凯， 吴海莉

(西南交通大学 力学与工程学院，成都610031)

断裂韧度是评价航空材料性能的一项重要指标而广受关注。党宁等［1］研究退火对ZTi6Al4V 钛合金断裂韧度的影响，曹晶晶等［2］研究了助溶剂对原位转化炭纤/氧化铝复合材料的断裂韧度的影响，最近的众多研究显示断裂韧度是材料研究者们关注的主要性能指标。有效的断裂韧度评价方法才能提供更为准确有效的实验数据。

紧凑拉伸(compact tension，CT)试样是断裂韧度测试规范［3～5］所推荐的标准试样构形之一。若在裂纹嘴位置测量裂纹张开位移则称为直通型CT(straight-notched CT)试样［6，7］。该类试样操作便利，在特殊服役环境下断裂性能的实验室测定时得到应用，如辐照环境下核反应堆压力容器钢的J 阻力曲线评定［8］。在现行测试规范中，仅提供针对台阶型CT 试样(即测量加载线位移)完整的J 积分计算公式，而对于直通型CT 试样，无论是ISO、国标中推荐的柔度法，还是ASTM 中推荐的载荷分离法，均未提供完整的J 积分算式，其关键在于缺乏用于塑性J 积分计算的塑性因子ηp，且ASTM 中现有的载荷分离式存在明显的量纲不等问题。对于直通型CT 试样的J 阻力曲线评定，有效的方法是将测得的裂纹嘴张开位移V0换算为加载线位移VLL，然后按照台阶型CT 试样的计算公式获得J 阻力曲线。对于直通型CT 试样的V0-VLL换算关系，蔡力勋，金蕾，包陈等［9～12］分别提出了裂尖小范围屈服条件下以及发生较大转动时直通型CT 试样对应的V0-VLL转换公式，但所得公式的精度还有待进一步讨论。本工作对现有载荷分离理论进行完善，解决量纲不等问题。通过有限元精细分析，推导得到精度较高且形式简单的V0-VLL转换公式，并采用三种工程材料实现直通型CT 试样获取断裂韧度的测试方法。

1 用于断裂韧度测试的载荷分离理论

现有载荷分离理论［13～15］指出，试样单位厚度上所承受的载荷P 可以表示为试样几何函数G(a/W)与试样变形函数H(Vp/W)的乘积:

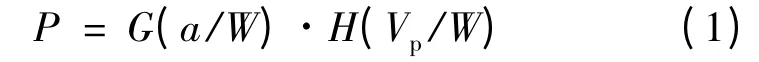
式中，a 为试样裂纹长度，W 为试样宽度，Vp为试样塑性变形。为了验证不同试样构型载荷分离假设的成立性，定义了载荷分离参数Sij:

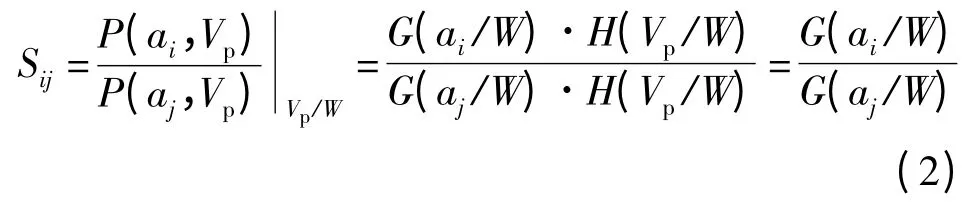
由此可见，对某种构型试样，若Sij在整个Vp范围内保持恒定，则载荷分离法成立。CT 试样裂纹几何函数G(a/W)可表示为:

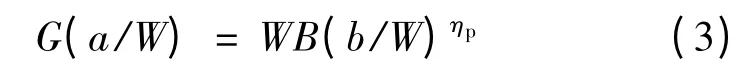
式中，B 为试样厚度，b 为试样剩余韧带长度，ηp为塑性因子。

载荷分离式(1)存在明显的量纲不等问题，违背量纲相似理论。为此根据π 定理，可以考虑引入参考载荷Pr对载荷分离理论进行改进，于是载荷分离理论可以修正表述为:

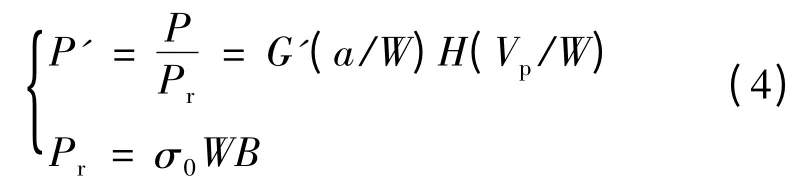
其中σ0为材料名义屈服应力。结合式(4)及式(2)，定义新的载荷分离参数S'ij，以此验证载荷分离的成立性:

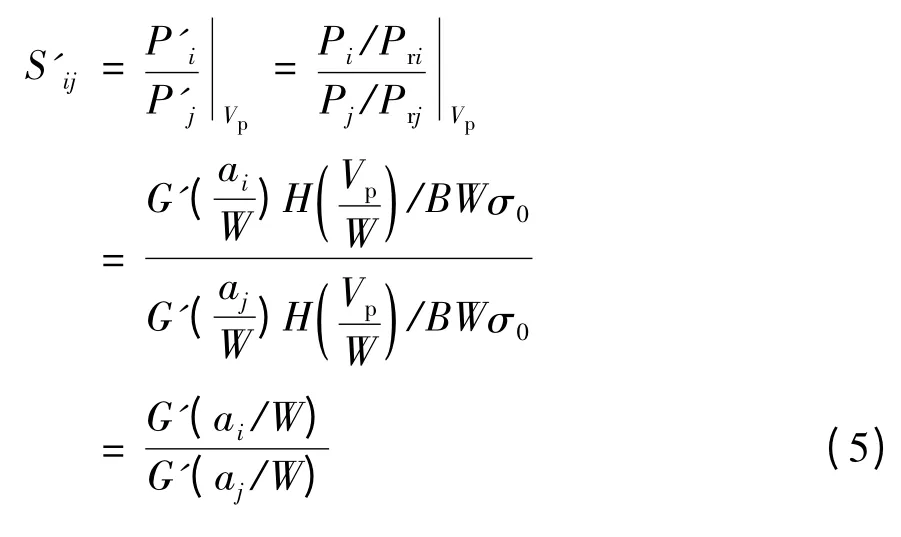
与现行载荷分离法类似，对于同种材料初始裂纹长度不同的两个钝裂纹试样，若在加载过程中S'ij保持恒定，则该构型试样载荷分离理论成立。

基于改进的载荷分离理论，在规则化法中［14］，将载荷P' 除以几何函数G'得到规则化载荷P'N，其中G'函数可由有限元结果拟合得到:

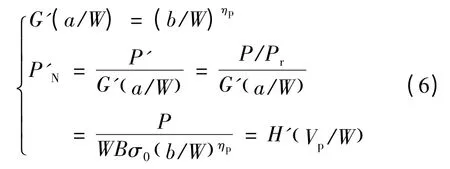
由上式可知，无量纲规则化方法的关键技术在于P'N-Vp/W 曲线的标定。参考ASTM 标准，对SET试样的P'N-Vp/W 曲线标定步骤为:将试验结束时的载荷、位移数据用最终裂纹长度af进行规则化处理，从裂纹终止数据点(Pfinal，Vfinal)作切线到经由a0进行规则化处理的数据点。除去Vp/W ＜0.001的数据点以及切点右边的数据点外(但包含裂纹终止点)，将(P'N，Vp/W)数据按式(7)进行拟合，由标定点确定式中参数c0，c1，c2和c3，进而求解实时裂纹长度a 及J 阻力曲线。

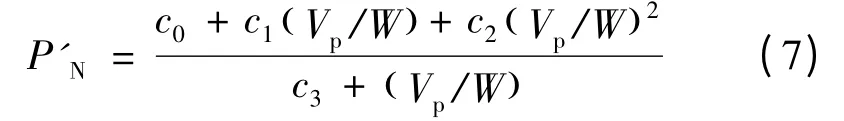
2 直通型CT 试样的COD 转换新公式

2.1 有限元网格精度研究

对于符合幂律硬化特征的大变形材料，其单轴本构关系可用Hollomon 模型描述［16］:

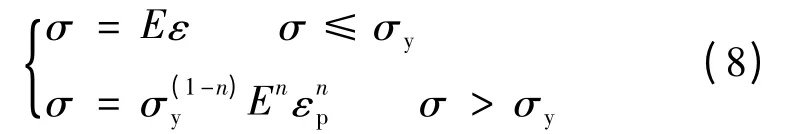
其中，n 为应变硬化指数，σy为名义屈服应力，σp为塑性应变。有限元分析表明，弹性泊松比对计算结果无影响，故取为0.3。为了得到适用范围较为广泛的COD 转换公式，考虑不同初始裂纹长度(a/W=0.5 ～0. 7)及不同材料硬化水平(σy= 100 ～800MPa，n=0.05 ～0.3)进行分析。

有限元计算时，选定单元之后，网格密度对结果的精度会产生显著的影响。一般来说，随着网格密度的增加，计算精度会随之提高，但盲目增加，不仅会使计算时间成倍上涨，有时还会影响计算精度［17］。为确定合理的模型网格密度，对直通型CT 试样不同裂尖网格密度进行对比计算。定义裂尖2mm 范围内网格数约为8000 时为一倍网格密度，后继网格模型以该裂尖区网格数的倍数来加密。图1 所示为直通型CT 试样不同网格密度与20 倍网格密度工况下VLL结果之间的相对误差。由图可知，随着网格密集程度的增加，相对误差逐渐减小并趋于稳定，因此综合考虑计算成本、计算精度等因素，确定采用如图2 所示的8倍网格密度进行有限元分析。

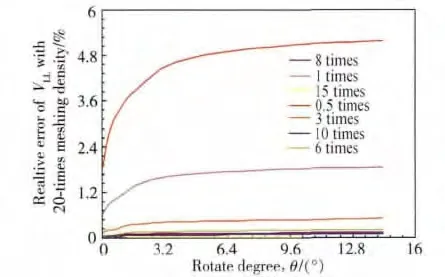
图1 不同裂尖网格密度加载线张开位移VLL与20 倍网格密度结果之间的相对误差Fig.1 Relative errors of VLL between different mesh density and 20 times

图2 有限元计算模型Fig.2 Finite element model

2.2 有限元精细计算结果分析

文献［11］基于台阶型CT 试样(stepped-notch CT，即在加载线测量裂纹张开位移的CT 试样)和直通型CT 试样的裂纹长度柔度计算式推导裂尖小范围屈服条件下直通型CT 试样的V0-VLL换算公式:

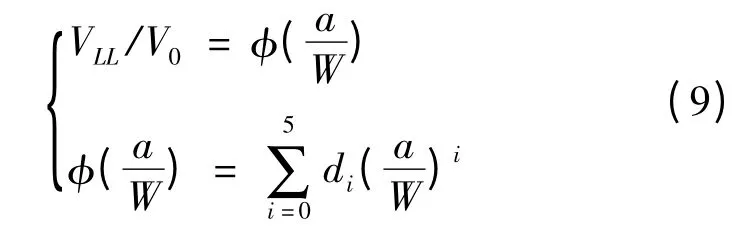
式中，a 为裂纹长度，W 为试样宽度，系数di分别为d0= 0. 2255，d1= 1. 8352，d2= － 2. 8064，d3=1.8742，d4=0.3276，d5= －0.6812。

文献［12］根据刚性转动假设和功等效的方法，推导了直通型CT 试样在裂纹面发生较大转角时的VLL-V0转换公式:

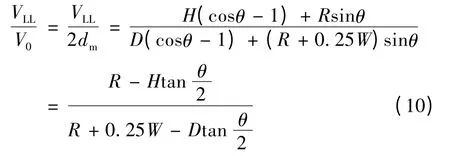
其中，dm为直通型CT 试样裂纹嘴缺口张开位移V0测量值的一半，R 为转动半径，H 为加载孔中心到裂纹面的距离，θ 为直通型CT 试样两裂纹面绕转动中心转角的一半，D 为裂纹嘴COD 引伸计标距的一半。转动半径R 可由下式进行计算:

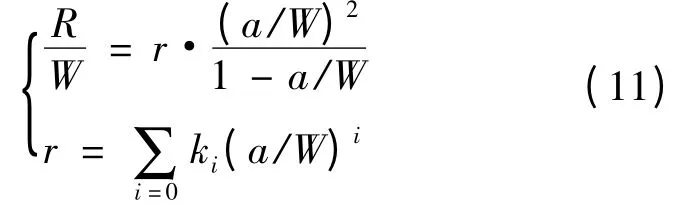
其中，k0=150.1554，k1= －1427.620，k2=5712.630，k3= －12131.87，k4=14357.50，k5= －8967.939，k6=2309.530。

有限元计算结果如图3 所示，图中仅列出两种裂纹长度对应的计算结果，其余a/W 结果均有类似趋势。由图分析可知，上述各公式与有限元结果之间均存在较大误差。由于影响V0-VLL换算公式精度的因素较多，要得到考虑众多因素的统一表达式较为困难，因此，需提出一个形式简单且精度较高的转换关系式。

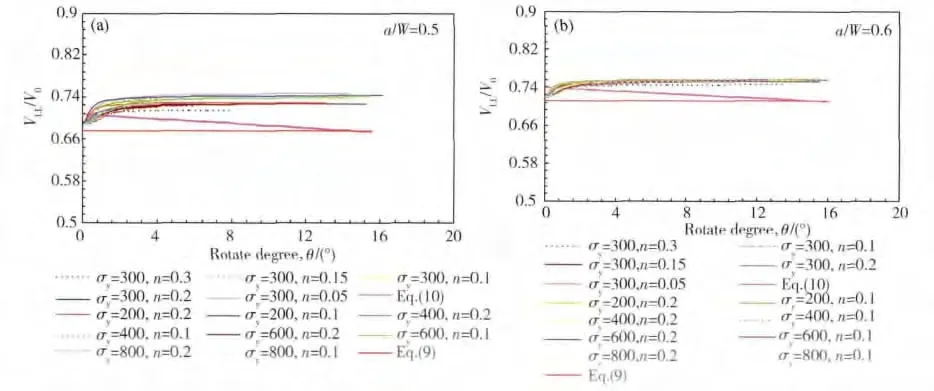
图3 不同裂纹长度a/W、不同材料对应的转换比VLL/V0Fig.3 Results of VLL/V0 for different crack length a/W and material properties (a)a/W=0.5;(b)a/W=0.6

2.3 直通型CT 试样的COD 转换新公式

当转动角度较小时，转动中心与材料的属性相关，其中需考虑的非线性参量较多，因此得到与所有材料常数耦合的精确函数关系较为困难，故依据图4 所示几何关系，提出如下转换公式。

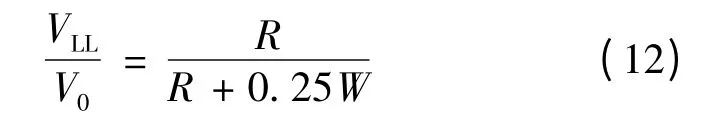
其中，转动半径R 由式(11)计算。该公式形式十分简单，忽略直通型CT 试样转动的影响，且与材料参数无关，计算方便。

对上述不同转换公式与有限元结果之间的最大相对误差进行分析，可以看出，当0.5≤a/W≤0.7时，本工作提出的COD 转换公式的误差集中在1%左右，较原有公式精度有了较大改善，且形式简单，计算方便。

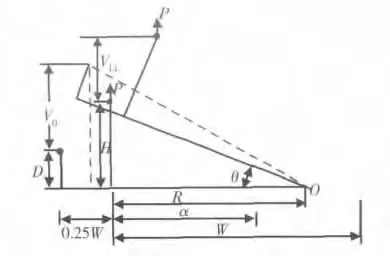
图4 直通型CT 转动图解Fig.4 Schematic explanation for rotation correction of Straight-notch CT specimen

直通型CT 试样无量纲载荷分离法求解流程如图5 所示。其中包含式(11)转换半径R 中实时裂纹长度a 的求解过程，即根据试验结束之后由工具显微镜测得的初始裂纹长度a0和终止裂纹长度af可建立实时裂纹长度a 的线性表达式，将此作为裂纹长度a 的第一次迭代值a1，带入转换公式中可以得到加载线位移VLL，由无量纲规则化方法处理即可得到新的实时裂纹长度a2和相应的J 积分值J2，由于试验中的裂纹长度并不是线性增长，因此此时得到的J 积分值并不准确。将a2代入式(11)中重复上述过程，直到Ji+1=Ji时迭代结束，此时得到的即为真实的裂纹长度a 和J 积分值。进而可计算相应的断裂韧度值。

2.4 转换公式的有效性验证

选取P91 管材10Cr9Mo1VNbN 加工不同初始裂纹长度(a/W=0.7，0.65，0.6，0.55 和0.5)CT 钝裂纹试样，如图6 所示，该类试样在加载过程中裂纹不发生扩展。钝裂纹试样裂纹顶端的圆孔直径为3mm，采用双燕尾槽设计，可同时测得裂纹嘴张开位移V0和加载线VLL。该合金的弹性模量E =2.06 ×105MPa，屈服强度σs= 490MPa，抗拉强度σb=650MPa。试验设备为美国电液伺服材料试验机MTS809 (250KN)，TestStarII 控 制 系 统，采 用MTS632.03F-30(标距为12mm)COD 引伸计测量试样裂纹嘴张开位移，MTS632.02F-20(标距为5mm)COD引伸计测量试样加卸载张开位移。试验机载荷传感器和应变引伸计精度为0.5 级。通过计算机对试验过程进行闭环控制和实时数据采集。加载过程为位移控制，速率为0.02mm/s，当加载线COD 引伸计达到4mm 时停止试验。验证试验装置如图7 所示。表1 给出各转换公式与试验结果的最大相对误差。

图7 验证试验Fig.7 Experimental facility

由表1 中结果可以看出，当0. 5 ≤a/W≤0. 7时，本工作提出的新公式与试验结果的最大误差均在1.3%以内，特别在0.5≤a/W≤0.65 区间内，新公式与试验结果误差均小于1%。可见，本工作的转换公式计算精度比较高，且表达形式简洁。

3 直通型CT 试样断裂韧度试验

选取汽轮机低压转子材料 1Cr12Mo，30Cr2Ni4MoV 以及P91 管材10Cr9Mo1VNbN 分别加工成图8 所示的初始裂纹长度不同的尖裂纹试样，低压转子材料的拉伸力学性能如表2 所示。试验前采用等ΔK 方式对试样进行疲劳裂纹预制，为了裂纹均匀扩展，预制裂纹完成后对剩余韧带部分开侧槽。将试样以位移控制方式进行单调加载，速率为0.02mm/s，当载荷下降5%之后停止试验。将试样取下进行热着色，然后以二次疲劳方式勾划裂纹前沿，打开试样(如图9)并在工具显微镜下按照9 点平均法测量试样预制后的裂纹长度及试验终止时的裂纹长度。

表1 10Cr9Mo1VNbN 钝裂纹试样试验结果与各公式最大误差Table 1 The maximum errors between test results and equations mentioned

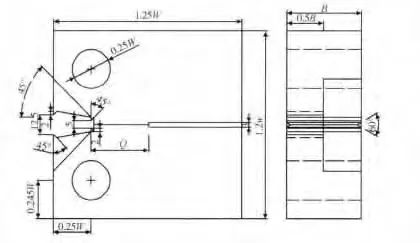
图8 CT 尖裂纹试样构形Fig.8 Crack-tip CT specimen

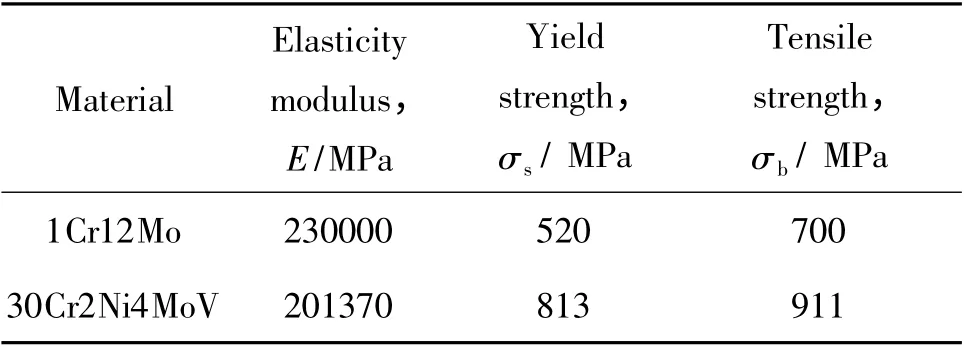
表2 各材料拉伸力学性能Table 2 Material properties of tension

图9 CT 试样裂纹断面Fig.9 Crack section of CT specimen

试验测试中得到了裂纹嘴张开位移V0，通过本工作提出的转换公式(12)可将其转换为加载线位移V'LL。图10 ～图12 所示分别为由载荷分离法得到的三种合金尖裂纹试样的JR阻力曲线。图中同种材料、同一试样对应着两条JR曲线，其中一条为由试验测得的加载线位移VLL计算得到，另一条则为由裂纹嘴张开位移转换为加载线位移V'LL计算得到。可以看出，同种材料同一试样的两条阻力曲线几乎重合，最大相对误差均在5%以内。

根据国标GB/T 21143—2007［3］，拟合JR阻力曲线时，至少需要六个数据点，且在四个等间距裂纹扩展区内，至少有一个数据点才为有效，如图13 所示。过Δa 最大值点作钝化线的平行线，与横坐标的交点定义为Δamax，该值应满足:

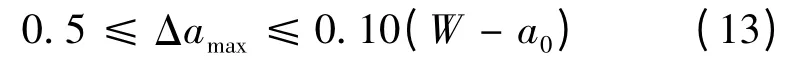
其中钝化线方程为:

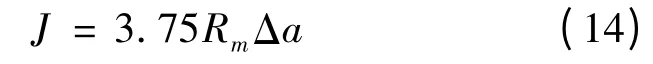
式中，Rm为试验温度下的抗拉强度。将过Δamax点钝化线的平行线定义为有效裂纹扩展量的右边界，过Δa=0.1 处钝化线的平行线定义为左边界线，最小Jmax为JR曲线上边界线。其中，试样的Jmax按照如下公式计算:

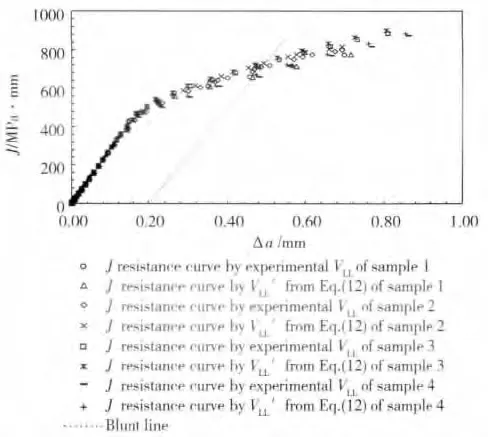
图10 10Cr9Mo1VNbN 材料JR 阻力曲线Fig.10 J resistance curves of 10Cr9Mo1VNbN

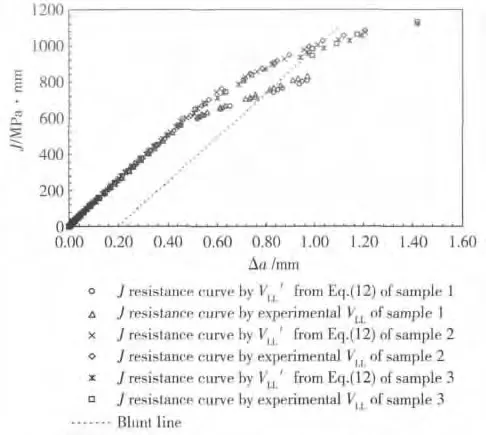
图11 1Cr12Mo 材料JR 阻力曲线Fig.11 J resistance curves of 1Cr12Mo

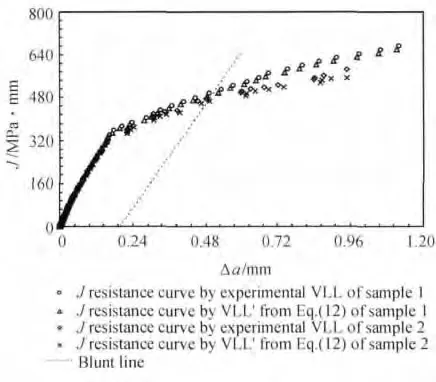
图12 30Cr2Ni4MoV 材料JR 阻力曲线Fig.12 J resistance curves of 30Cr2Ni4MoV

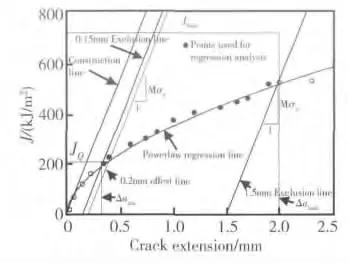
图13 有效性判定示意图Fig.13 The diagram of validity judgement

其中，Rp0.2为试验温度下的屈服强度。

对0.1mm 和Δamax边界线之间的数据点按如下所示指数方程拟合JR阻力曲线。

表3 所示为各合金试样对应的断裂韧度值以及JR阻力曲线参数拟合结果。钝化线的0.2mm 偏置线与 JR阻力曲线的交点即为 JQ。对于30Cr2Ni4MoV 合金符合如上所述有效性判据，固该合金的JIC平均取值为418MPa·mm。

4 结论

(1)提出了修正的载荷分离公式P' = P/Pr=G'(a/W)H(Vp/W)，Pr= σ0WB，并根据有限元计算给出了几何函数G'的表达式，使得载荷分离理论符合π 定理。

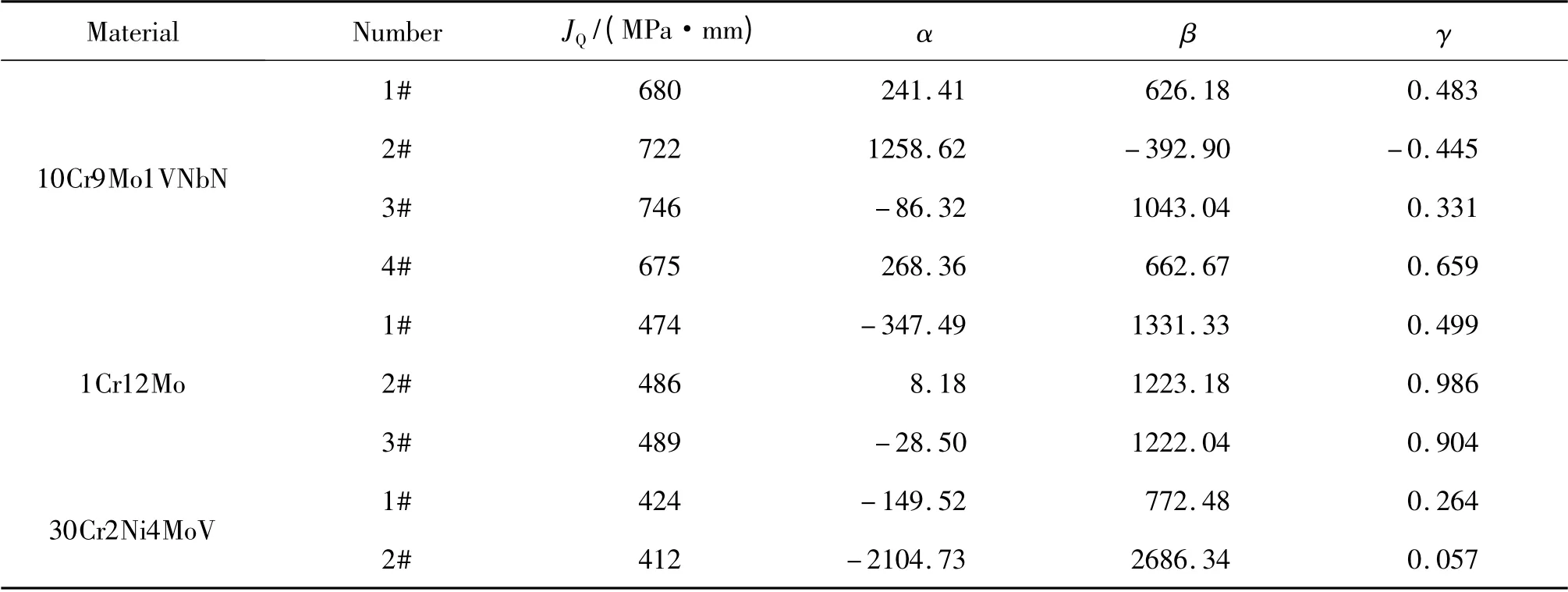
表3 各合金尖裂纹试样断裂韧度值Table 3 The fracture toughness properties of three materials

(2)基于对直通型CT 试样的精细有限元分析，提出了精度高、形式简洁的COD 转换公式VLL/V0= R/(R +0.25W)，进而提出了基于直通型CT 试样的断裂韧度载荷分离测试新方法。

(3)根据本工作提出的方法，采用不同初始裂纹长度10Cr9Mo1VNbN 钝裂纹CT 试样对新转换公式的有效性和精确性进行了试验验证，结果表明误差均小于1. 3%。通过载荷分离法获得了1Cr12Mo， 30Cr2Ni4MoV 以 及 P91 管 材10Cr9Mo1VNbN 三种材料的断裂韧度和JR阻力曲线，试验值与公式计算值的最大相对误差均在5%以内。

［1］党宁，赵嘉琪，南海，等. 退火态ZTi6Al4V 铸造钛合金的断裂韧度研究［J］. 航空材料学报，2012，32 (4):87－91.(DANG N，ZHAO J Q，NAN H，et al.Fracture toughness of ZTi6Al4V casting titanium alloy under different annealed conditions［J］. Journal of Aeronautical Materials，2012，32(4):87 －91.

［2］曹晶晶，陈华辉，杜飞，等. 助熔剂对原位转化炭纤维/氧化铝复合材料组织结构与性能的影响［J］.材料工程，2013(12):54 －58.(CAO J J，CHEN H H，DU F，et al.Effect of sintering additives on microstructures and properties of in-situ transformed carbon fiber/alumina composites［J］. Journal of Materials Engineering，2013(12):54 －58.

［3］刘涛，高怡斐，李颖，等. GB/T 21143—2007 金属材料准静态断裂韧度的统一试验方法［S］. 北京:中国标准出版社，2008.

［4］International Organization for Standardization. ISO 12135-2002(E)International standard of unified method of test for the determination of quasistatic fracture toughness［S］.Switzerland:International Organization for Standardization，2002.

［5］ASTM International. ASTM E1820-08a Standard test methods for measurement of fracture toughness［S］. Annual Book of ASTM Standards:Vol 301. Philadelphia，PA:American Society for Testing and Materials，2008.

［6］姚蘅. ASTM E813—87 JIC断裂韧性试验方法:节译稿［S］. 北京:冶金部钢铁研究总院，1988:20 －37.

［7］姚蘅，邓枝生，邓其源. GB/T 2038—1991 金属材料延性断裂韧度JIC试验方法［S］. 北京:中国标准出版社，2002:387 －411.

［8］RICE J R，BOSENGREN G F. Plane strain deformation near a crack tip in a power-law hardening material［J］.Journal of the Mechanics and Physics of Solids，1968，16(1):1 －12.

［9］蔡力勋，陈洪军，包陈. 关于断裂力学柔度测试技术的新思考［J］. 核动力工程，2006 (10):134 －138.(CAI L X，CHEN H J，BAO C. The new thought of compliance testing technology about fracture mechanics［J］. Nuclear Power Engineering，2006 (10):134 －138. )

［10］蔡力勋，包陈，金蕾. 金属材料断裂力学柔度测试技术问题与发展［J］. 中国测试，2009，35(1):9 －18.(CAI L X，BAO C，JIN L. Compliance testing technology used for fracture properties of metallic materials :problems and development［J］. China Measurement and Test，2009，35(1):9 －18.)

［11］金蕾，蔡力勋. 基于材料断裂韧度测试的COD 换算方法研究［J］.机械强度，2010，32(1):116 －120.(JIN L，CAI L X，BAO C. Study on crack open displacement transform formulas based on testing of material fracture toughness［J］. Journal of Mechanical Strength，2010，32(1):116 －120.)

［12］包陈，蔡力勋，石凯凯. 直通型CT 试样COD 弹塑性换算研究［J］. 北京科技大学学报，2011，33(7):863 －867.(BAO C，CAI L X，SHI K K. Study on crack opening displacement elastic-plastic transform formula for front-force compact tension (FFCT)specimen［J］. Journal of University of Science and Technology Beijing，2011，33(7):863－867.)

［13］EMST H A，PARIS P C，LANDES J D. Estimations on Jintegral and tearing modulus T from a single specimen test record［J］. Fract Mech，ASTM STP 743，American Society for Testing and Materials，1981:476 －502.

［14］SHAROBEAM M H，LANDES J D. The load separation criterion and methodology in ductile fracture mechanics［J］. Int J Fract，1991，47:81 －104.

［15］WAINSTAIN J，FRONTINI P M，CASSANELLI A N. J-R curve determination using the load separation parameter Spbmethod for ductile polymers［J］. Polym Test，2004，23:591.

［16］HOLLOMON J H. Tensile deformation［J］. Aime Trans，1945，12(4):1 －22.

［17］高素荷. 网格划分密度与有限元求解精度研究［J］. 机械设计，2007，27:161 －163.(GAO S H. The theory and practice of high speed raster photography［J］. Mechanical Design，2007，27:161 －163.)