基于小裂纹理论的GH4169高温合金的疲劳全寿命预测

张 丽， 吴学仁

(北京航空材料研究院 航空材料检测与评价北京市重点实验室 先进高温结构材料国防科技重点实验室，北京100095)

基于断裂力学研究长裂纹和小裂纹(10 μm ～1 mm)扩展行为时，发现“小裂纹效应”的存在，即在相同的名义应力强度因子范围ΔK 的作用下，小裂纹的扩展速率高于长裂纹，并且在低于长裂纹扩展门槛值ΔKth的情况下小裂纹仍能扩展［1，2］。“小裂纹效应”已经在试验中得到证实，尤其在压缩加载，如负应力比条件下更为明显。小裂纹和长裂纹扩展行为的差异通常认为是由于疲劳裂纹闭合现象引起的。疲劳裂纹闭合是由于残留在前进中的裂纹尾迹上的塑性变形引起的。大量的研究［3～7］表明，金属材料和结构的疲劳裂纹主要起始于材料初始微观结构缺陷，如加工划痕、夹杂颗粒、孔洞或滑移损伤等。这使得裂纹起始寿命大大缩短。同时也使得小裂纹没有能够导致闭合的尾迹塑性变形的历史，因此小裂纹的闭合程度不及长裂纹。如果小裂纹是完全张开的，则应力强度因子范围全部有效，因而裂纹扩展速率将比稳定状态的裂纹扩展速率大。而长裂纹门槛值是随着载荷下降时裂纹闭合上升而建立起来的。因此稳定状态的裂纹扩展行为将可能介于小裂纹与长裂纹门槛行为之间。

自20 世纪80年代中期以来，国内外疲劳断裂界对小裂纹扩展行为，对经典的S-N 疲劳/耐久性与现代损伤容限之间的联系，以及利用断裂力学原理进行疲劳全寿命预测的可行性进行了系统深入的研究。北京航空材料研究院与美国国家航空航天局(NASA)兰利研究中心对中美两国的两种航空高强铝合金曾进行了长达8年的合作研究，发展了一种基于断裂力学理论，把ΔK 与裂纹闭合概念相结合，适用于小裂纹扩展分析的全寿命预测方法，即基于小裂纹理论的疲劳全寿命预测方法［1，2］。“小裂纹理论”是指将疲劳过程处理为裂纹从微缺陷(或微裂纹)至断裂失效的扩展过程。这也是应用该寿命预测方法的基本前提。

GH4169(Inconel718)是一种沉淀强化镍基高温合金，被广泛应用于航空发动机构件，齐欢［8］总结了合金的发展过程。合金的疲劳性能也受到关注，近期黄嘉等［9］研究了惯性摩擦焊后焊接接头的疲劳性能。在以往对该合金小裂纹行为的研究中，也发现了“小裂纹效应”的存在。Connolley 等［10］和Huang 等［11］在各自的研究中均发现了该合金在疲劳早期，材料夹杂开裂形成微裂纹，裂纹的起始寿命所占比例非常小。从目前对GH4169 合金疲劳裂纹扩展行为的研究来看，该合金已经满足了基于小裂纹理论的疲劳全寿命预测方法的基本前提条件。

本工作以航空发动机涡轮盘用高温合金GH4169 材料为研究对象，进行了室温恒幅载荷作用下应力比为0.1 和0.5 的小裂纹和长裂纹扩展试验，以及单边缺口拉伸试样的高周疲劳试验。基于小裂纹理论的疲劳全寿命预测模型，采用FASTRAN软件［12］对GH4169 合金的疲劳全寿命进行预测，并利用高周疲劳试验S-N 数据来验证该方法的适用性。

1 材料与试验

试验材料为涡轮盘用镍基高温合金GH4169，其热处理制度为直接时效热处理。合金微观结构如图1 所示。平均晶粒尺寸约为15μm，个别晶粒尺寸达到50μm 左右。该合金中存在两种不同形貌的夹杂:颜色较深的为Ti(C，N)，多为方形，尺寸为5 ～30μm;颜色较浅的为Nb(C，N)，形状、大小各异。材料在室温下的拉伸性能为σ0.2=1390MPa，σb=1530MPa。

图1 GH4169 合金的微观结构Fig.1 Microstructure of superalloy GH4169

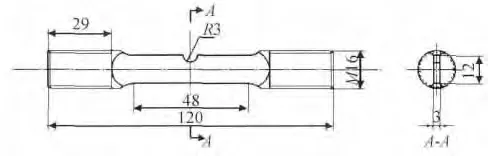
图2 SENT 试样形状和尺寸Fig.2 Geometry and sizes of SENT specimen (unit:mm)

考虑到涡轮盘的一种服役损伤形式是在枞树形根部或螺栓孔等处产生疲劳裂纹，盘的定寿必须考虑缺口处的疲劳行为。因此选择单边缺口拉伸(SENT)试样作为小裂纹试样和高周疲劳试样，试样的形状和尺寸如图2 所示。试样缺口根部的应力集中使得此处容易产生如图3 所示的自然萌生的表面裂纹，裂纹起始于试样缺口根部，以半椭圆形裂纹扩展。采用弹性本构模型计算试样缺口基于毛截面的理论应力集中系数Kt为4.37。用于小裂纹试验的试样经过低应力机械抛光至镜面。采用薄膜复型法监测小裂纹起始和扩展过程。

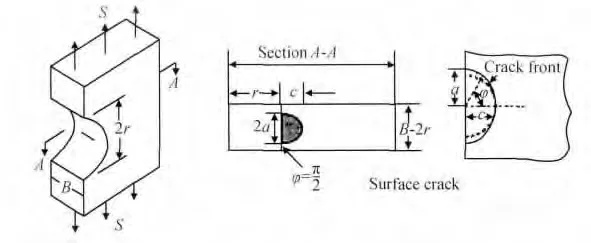
图3 GH4169 合金小裂纹起始位置及形状Fig.3 Small crack initiation site and shape of superalloy GH4169

GH4169 合金的长裂纹扩展数据通过对紧凑拉伸(CT)试样在恒幅载荷作用下的裂纹扩展行为来获得。试样宽度为40mm，厚度为10mm。所有试样均在涡轮盘上切取。

2 塑性诱导裂纹闭合模型

Newman 的塑性诱导的裂纹闭合模型［13，14］原本是针对有限宽板的中心裂纹建立的，随后又推广到孔边穿透裂纹。该模型是建立在Elber 的裂纹闭合概念和Dugdale 裂尖塑性区模型基础上的，但对后者又作了修正，即考虑了裂纹尾迹上的残留塑性变形。有关该模型的细节可参考文献［15］。但是，该模型一个最重要的特征是引入约束因子α 来模拟裂纹前缘的三维约束效应。

经循环塑性区修正的有效应力强度因子范围［16］由下式给出:

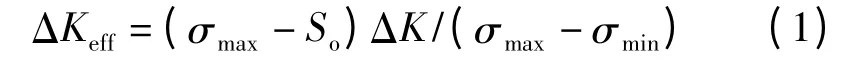
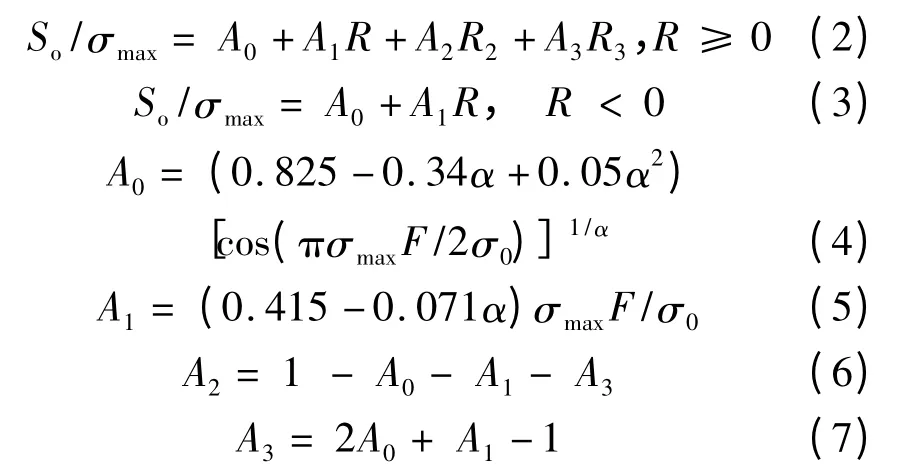
式中，σmax为最大应力，R 为应力比，So为裂纹张开应力，α 为应力状态约束系数，在1 ～3 中取值，1为平面应力，3 为平面应变，σ0为杆元流动应力，F为边界修正因子。

式(1)～(7)被用来建立裂纹扩展的da/dNΔKeff基线数据，这些基线数据被用在FASTRAN 程序中预测疲劳寿命。

3 裂纹扩展行为

为了进行疲劳全寿命预测，必须要有材料的裂纹扩展速率da/dN－ΔKeff基线数据。这需要通过长裂纹和小裂纹的扩展试验来确定，长裂纹的扩展曲线还可用于验证小裂纹效应是否存在。

3.1 小裂纹扩展行为

采用SENT 试样进行了应力比为0.1 和0.5 的小裂纹扩展试验，利用薄膜复型法记录了试样缺口根部沿缺口壁的小裂纹的起始和扩展过程。小裂纹均起始于试样表面的夹杂:Ti(C，N)和Nb(C，N)，并获得了不同循环周次对应的小裂纹长度的数据。大部分试样产生了一条导致断裂的主裂纹，仅三根试样产生了两条主裂纹，两条主裂纹同时扩展，在疲劳后期两条主裂纹合并，最终导致试样断裂。表1给出了这些试样的小裂纹长度和寿命等数据。采用薄膜复型法监测到的最小裂纹仅为十几个微米长。此处，Ni为首次发现小裂纹时的寿命，Np为小裂纹扩展寿命，该值由小裂纹扩展至穿透试样厚度时的寿命值减去Ni得到，Nf为试样断裂时的寿命，即疲劳全寿命。疲劳裂纹的起始寿命所占比例在8% ～39%之间，小裂纹的扩展寿命所占比例很大，在60% ～90%之间。这些结果表明，GH4169 合金具备基于小裂纹理论的疲劳全寿命预测模型的基本要求。

利用断裂力学理论进行裂纹扩展寿命预测的重要前提之一是高精度的应力强度因子解，即K 值。Wu 和Newman 等［17］基于三维权函数和有限元计算，得到了SENT 试样半椭圆表面裂纹K 值的计算式:

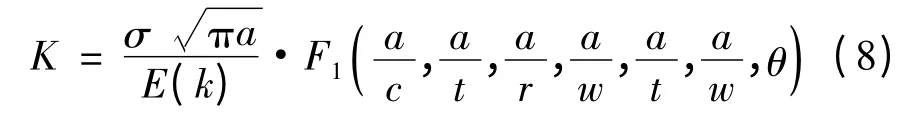
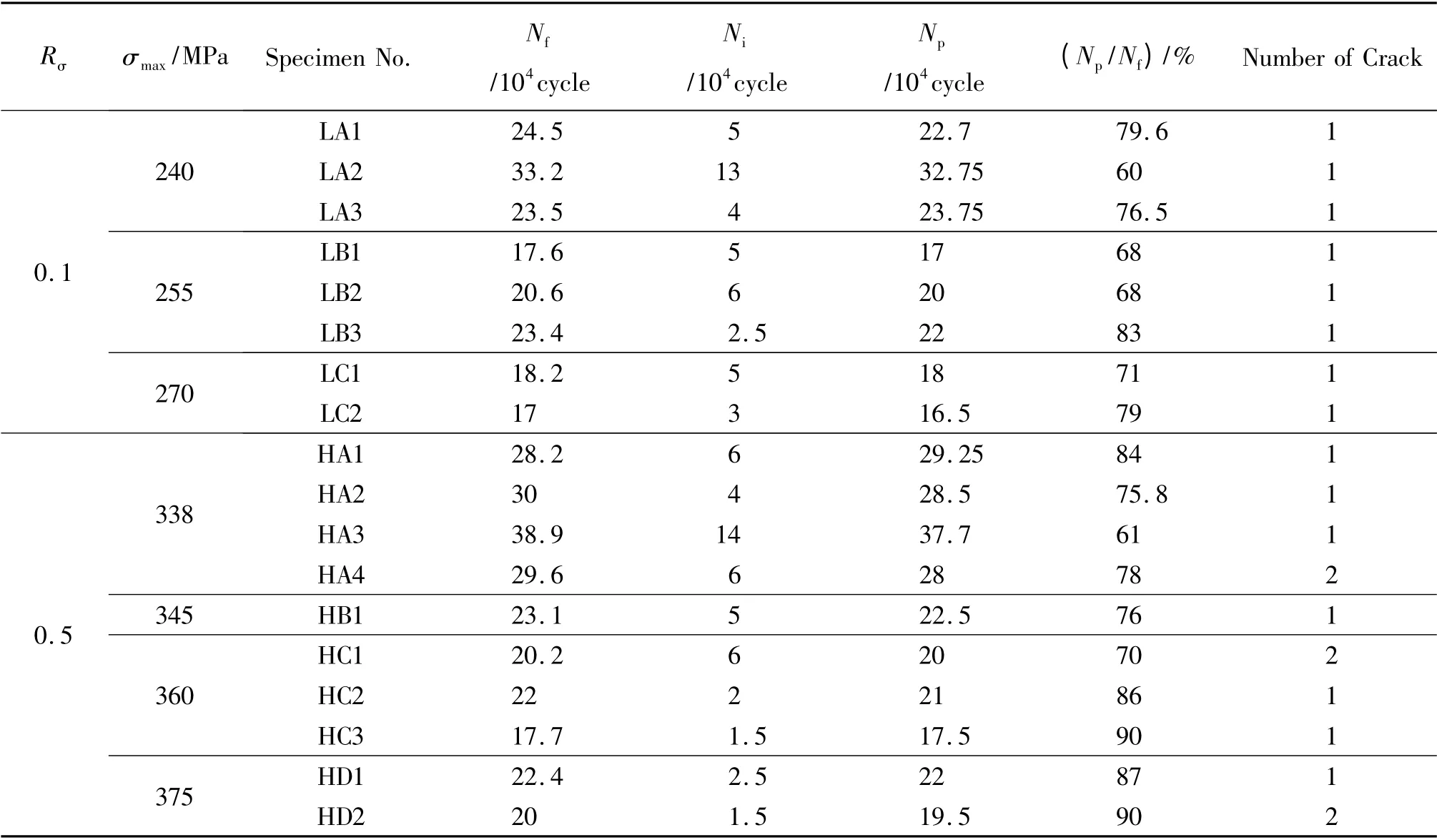
表1 小裂纹长度及寿命数据Table 1 Data of small crack lengths and lives

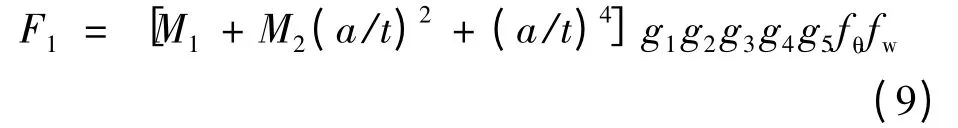
式中:σ 为名义拉伸应力;E(k)为形状因子;g1，g2，g3，g4，g5，fθ，fw的具体定义见文献［17］，在本工作的计算中假设裂纹长度a 与裂纹深度c相等。

采用割线法对薄膜复型法得到的(2a，N)数据进行计算，获得小裂纹扩展的da/dN 数据，与根据式(8)，(9)计算得到的ΔK 数据关联，得到如图4所示的小裂纹扩展数据。小裂纹扩展速率具有较大的分散性，尤其在低ΔK 区。同一应力比下，加载应力的变化对小裂纹扩展速率的影响不大。这些小裂纹数据将用于帮助选择近门槛值区的da/dN－ΔKeff基线数据。

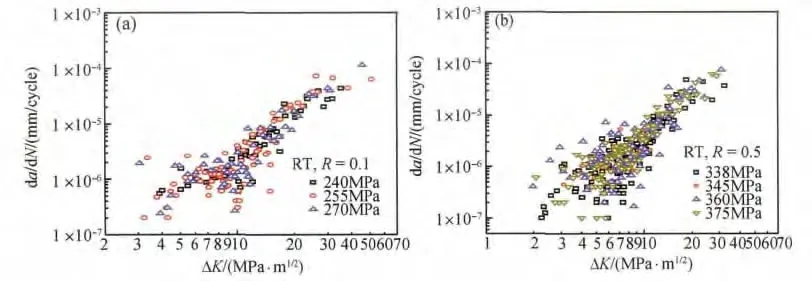
图4 小裂纹扩展数据Fig.4 Data of small crack growth (a)R=0.1;(b)R=0.5

3.2 长裂纹扩展行为

图5a 给出了CT 试样在应力比R = 0.1 和0.5下的长裂纹扩展数据。利用Newman 裂纹闭合公式(式(1)～(7))进行裂纹扩展速率da/dN 与ΔKeff的关联，如图5b 所示。通过试算发现，当约束系数α为2.5 时，所有的数据能归并到几乎是一条da/dNΔKeff的曲线上。图中实线是长裂纹扩展da/dNΔKeff基线数据。此处没有采用方程式来对裂纹扩展速率与ΔKeff做关联，而是选取了不同速率处对应的ΔKeff值，尤其在转折点，即建立了一个da/dN-ΔKeff对应的表格。这样做是因为表格能比多参量的方程式更为精确地描述基线数据，尤其在转折过渡区。

在门槛值区域，长裂纹扩展试验采用降载法，在达到门槛值后，再用升载法继续试验以获取更多的da/dN 数据。采用这种方法得到的近门槛值区域的数据很可能会受到裂纹闭合的影响，特别是在应力比R 不太高的情况下。因此，这样测得的门槛值以及近门槛值区域的数据不适用于小裂纹扩展速率的计算。该区域的基线数据将通过与小裂纹扩展数据的比较来进行估计。

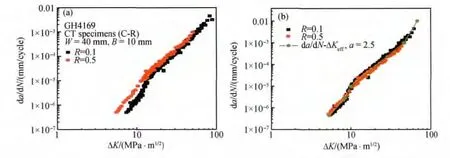
图5 长裂纹扩展数据Fig.5 Data of long crack growth (a)da/dN－ΔK;(b)da/dN－ΔKeff;

图6 给出了两个应力比下的长裂纹和小裂纹扩展数据的对比。图中若非特别说明，均为da/dNΔK 数据。由图可见，两种应力比下，该合金均有明显的小裂纹效应，尤其在近门槛值区域。因此，基于线弹性断裂力学进行寿命预测时，必须考虑小裂纹扩展行为，否则将会得到非保守的寿命估计。在高裂纹扩展速率区(da/dN ＞105mm/cycle)，小裂纹扩展速率基本上与长裂纹速率归并到一起。因此，该范围的长裂纹扩展da/dN－ΔKeff基线数据可用于寿命预测。但由于“小裂纹效应”的存在，在da/dN＜105mm/cycle 时，与小裂纹扩展速率偏差较大的数据将不适合用于寿命预测，必须根据小裂纹扩展数据进行估算，得到图6a 和图6b 中所示的虚线部分。

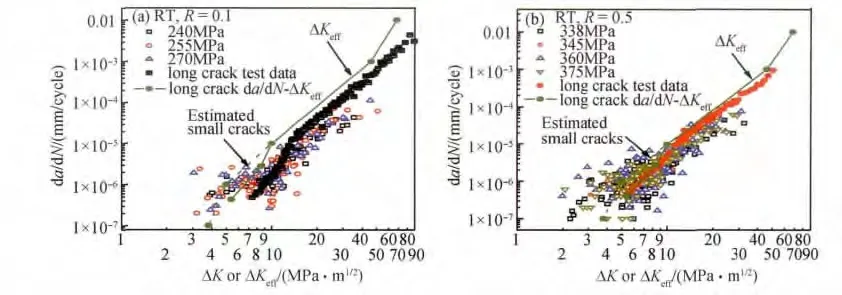
图6 长裂纹和小裂纹扩展数据对比Fig.6 Comparison of long－and small－crack growth data (a)R=0.1;(b)R=0.5

综合考虑小裂纹和长裂纹的扩展行为，得到用于寿命预测的da/dN－ΔKeff基线数据，见表2。表3给出了寿命预测中所选用的部分参数，其中E 为弹性模量，KF为断裂韧度，m 为断裂韧度参数。至此，已经得到FASTRAN 寿命预测的大部分数据，但仍缺少一个所需的主要条件，即初始裂纹尺寸ai和ci值。

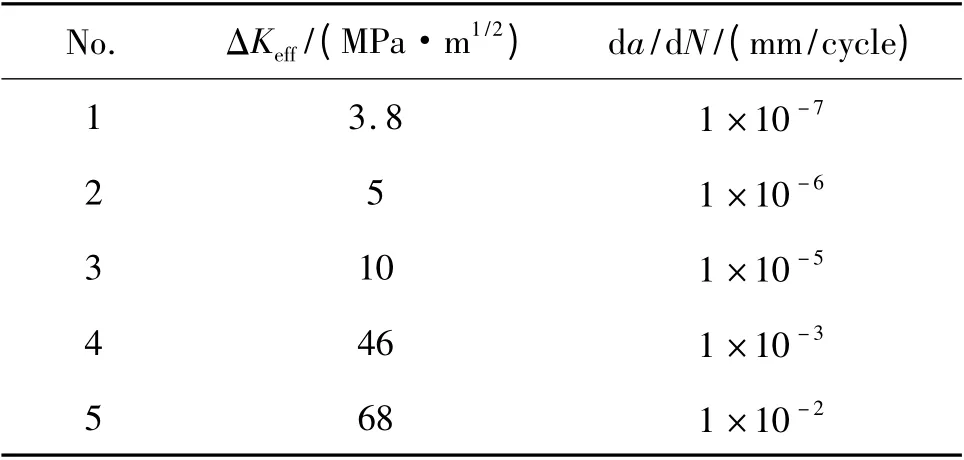
表2 da/dN－ΔKeff基线数据Table 2 The baseline data of da/dN－ΔKeff

表3 力学性能Table 3 Mechanic properties of GH4169

4 疲劳裂纹源分析

基于断裂力学的FASTRAN 寿命预测模型，初始裂纹尺寸是必需的主要条件，或称为等效初始缺陷尺寸(EIFS)。通常确定初始裂纹尺寸的方法有三种［18］:一是经验取值，二是根据试验结果迭代或外推，三是通过分析材料的金相照片或试样的疲劳断口形貌来确定。显然，第三种方法更加直接准确。本工作采用对疲劳试样的断口形貌分析的方法来确定初始裂纹尺寸。

采用SENT 试样进行了应力比为0.1 和0.5 的高周疲劳试验，试验方法按照HB 5287—1996 进行，得到了疲劳寿命区间为5 ×104～1 ×107循环周次的寿命数据。该试验目的有三:(1)对试样断口形貌进行观察分析，获得该合金疲劳裂纹源的信息;(2)对疲劳极限进行试算得到(ΔKeff)th值;(3)利用高周疲劳S-N 数据对FASTRAN 预测模型进行评价。

利用扫描电子显微镜(SEM)和能谱分析仪(EDS)对试样断口形貌进行观察分析，发现疲劳裂纹均起源于试样表面的夹杂，如图7 所示。Murakami［19］提出，对于形状不规则的裂纹(如夹杂、孔洞等缺陷起始的裂纹)，不采用其真实面积来计算K 值，而采用能够将初始不规则形状全部包含在内的光滑轮廓所包含的面积作为等效面积。根据该原则对疲劳源区的夹杂进行等效面积处理，如图7 中虚线所示，得到的夹杂处的等效面积area。考虑到小裂纹起始后很快以半圆形裂纹向前扩展的情况，假设裂纹沿长度和深度方向的初始尺寸相等，即ai=ci，根据半圆的面积公式，计算得到初始裂纹尺寸，即

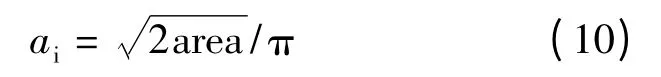
图7 疲劳源区扫描电镜照片Fig.7 SEM photos of fatigue initiation sites

对计算得到的初始裂纹尺寸进行统计，裂纹尺寸分布在5 ～20μm。将所有尺寸分为八个区间作为横坐标，每2个微米为一个区间，分别为5 ～7μm，7 ～9μm 至17 ～19μm，最后一个区间为19 ～20μm。以每个区间内初始裂纹的个数为纵坐标得到如图8所示的结果。可见夹杂尺寸ai=ci主要分布在7 ～9μm 和9 ～11μm 区间内。

5 疲劳寿命预测

至此，已经具备了对一个疲劳全寿命方法进行评价的所有条件。该寿命预测方法的全部基础是由起源于材料的微观缺陷处(在GH4169 合金中微观缺陷为材料夹杂)的裂纹扩展。在这个全寿命预测方法中，假设在第一个循环时裂纹就已经存在并开始扩展。利用裂纹闭合模型和基准的da/dN－ΔKeff曲线来预测从初始裂纹尺寸(即材料夹杂)直至断裂的全过程的裂纹扩展行为。利用SENT 试样的疲劳试验结果对预测结果进行评价，模型的流程如图9 所示。

图8 初始缺陷尺寸统计分布Fig.8 Statistical distribution of initial defect sizes

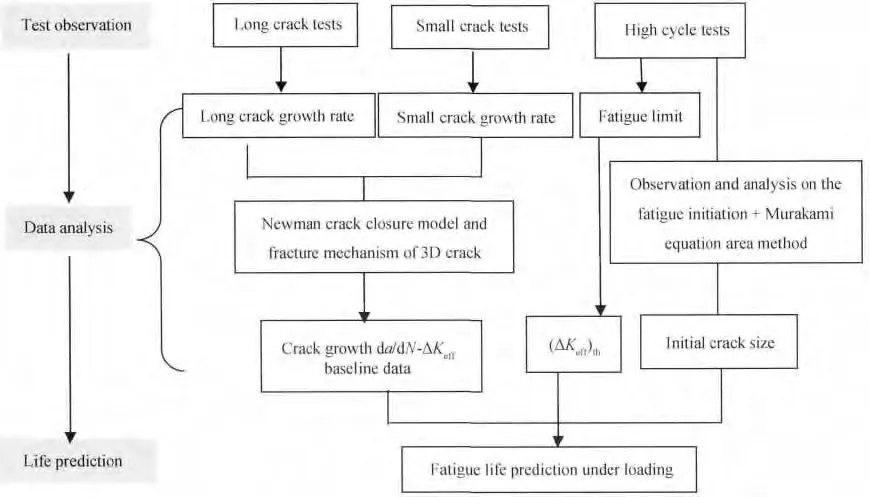
图9 FASTRAN 模型的总体流程图Fig.9 General scheme of the model presented in FASTRAN

根据图9 所示的FASTRAN 模型总体方案流程计算得到了GH4169 合金在恒幅载荷下的疲劳寿命(S-N)数据，见图10，无箭头符号表示试样做到断裂，带箭头符号表示试验在试样断裂前就停止了。初始裂纹尺寸ai=ci分别取7 ～11μm 范围内不同的值进行试算，初始裂纹半高bi=0μm。采用的有效应力强度因子范围与裂纹扩展速率的关系见表2。利用FASTRAN 程序对疲劳全寿命作了预测，图中实线代表了预测的疲劳寿命。结果表明，当ai=ci=8μm 时，得到的预测结果与试验结果吻合良好。

为进一步评价FASTRAN 寿命预测程序，计算了不同初始裂纹尺寸的寿命值，并与试验数据作对比。根据试样断口分析结果可知大部分初始裂纹尺寸分布在7 ～11μm 范围内，故分别采用7μm 和11μm 作为裂纹初始尺寸，依然采用表2 给出的da/dN－ΔKeff基线数据来预测疲劳全寿命，结果如图11所示。采用这两个初始裂纹尺寸值计算得到的疲劳寿命，除少数几个点，均能很好地将试验数据包含在寿命分散带内。这些结果表明基于小裂纹理论的疲劳全寿命预测方法适用于对室温恒幅载荷作用下GH4169 合金疲劳全寿命的预测。

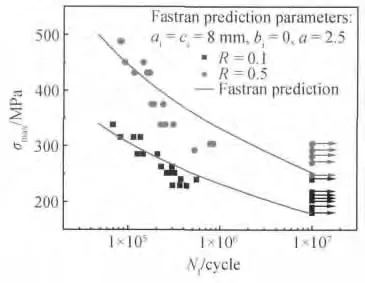
图10 SENT 试样的预测与试验疲劳寿命对比Fig.10 Comparison of experimental and predicted fatigue lives of SENT specimens

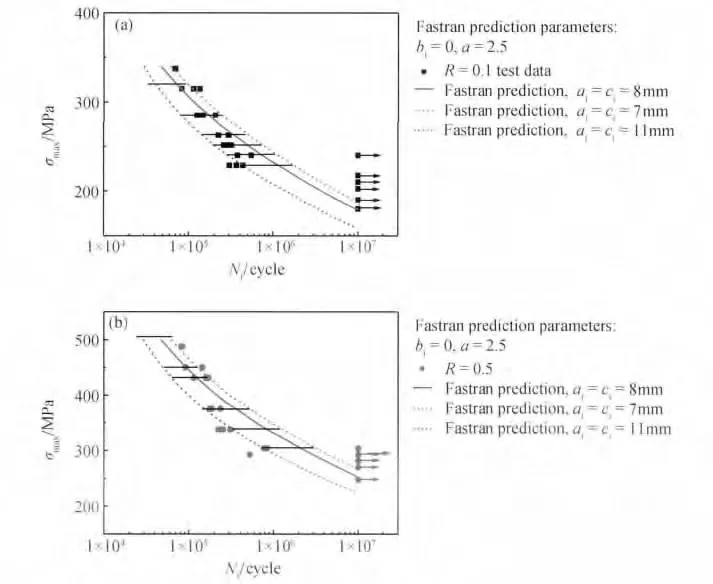
图11 寿命预测值与试验结果的对比Fig.11 S-N data comparison of predicted and experimental fatigue lives

6 结论

(1)室温下GH4169 合金的疲劳裂纹多起源于材料夹杂，疲劳全寿命的大部分消耗在小裂纹扩展阶段。在长裂纹扩展速率低于10－5mm/cycle 的区域，具有明显的小裂纹效应，寿命预测必须考虑小裂纹扩展行为。

(2)在疲劳试验过程中导致高周疲劳失效的夹杂物的等效初始裂纹尺寸ai主要分布在7 ～11μm范围内。

(3)当初始裂纹尺寸ai= ci= 8μm 时，利用FASTRAN 软件预测得到GH4169 合金的疲劳全寿命，预测结果与试验结果符合良好。分别以7μm 和11μm 作为初始裂纹尺寸，预测得到的寿命分散带，将大部分的试验数据包含在内。

［1］NEWMAN J C，WU X R，VENNERI S L，et al. Small crack growth and fatigue life predictions for high－strength aluminum alloys:part II :crack closure and fatigue analyses［J］. Fatigue and Fracture of Engineering Materials and Structures，2000，23:59 －72.

［2］吴学仁，刘建中. 基于小裂纹理论的航空材料疲劳全寿命预测［J］. 航空学报，2006，27(2):219 －226.(WU X R，LIU J Z. Total fatigue life prediction for aeronautical materials by using small－crack theory ［J］. Acta Aeronautica et Astronautica Sinica，2006，27(2):219 －226.)

［3］BARTER S A，MOLENT L，WANHILL R J H. Typical fatigue－initiating discontinuities in metallic aircraft structures［J］. International Journal of Fatigue，2012，41:11 －22.

［4］MURAKAMI Y. Material defects as the basis of fatigue design［J］. International Journal of Fatigue，2012，41:2 －10.

［5］BESEL M，BRÜCKNER－FOIT A，MOTOYASHIKI Y，et al. Lifetime distribution of notched components containing void defects ［J］. Archive of Applied Mechanics，2006，76:645 －653.

［6］LAZ P J，HILLBERRY B M. Fatigue life prediction from inclusion initiated cracks［J］. International Journal of Fatigue，1998，20:263 －270.

［7］周晓明，汪武祥，王旭青，等. SiO2非金属夹杂物对镍基粉末高温合金微观力学行为的影响［J］. 航空材料学报，2006，26(3):1 －6.(ZHOU X M，WANG W X，WANG X Q，et al. Effect of SiO2non－metallic inclusion on micro－mechanical behavior of nickel－base P/M superalloy［J］. Journal of Aeronautical Materials，2006，26(3):1 －6.)

［8］齐欢.INCONEL 718 (GH4169)高温合金的发展与工艺［J］.材料工程，2012(8):92 －100.(QI H. Review of INCONEL 718 alloy:its history，properties，processing and developing substitutes［J］. Journal of Materials Engineering，2012(8):92 －100.)

［9］黄嘉，季英萍，秦丽晔，等.GH4169 合金惯性摩擦焊接接头疲劳裂纹扩展性能［J］.航空材料学报，2013，33(6):45 －50.(HUANG J，JI Y P，QIN L Y，et al. Fatigue crack growth behavior of inertia friction welded joints of GH4169 alloy［J］.Journal of Aeronautical Materials，2013，33(6):45 －50.)

［10］CONNOLLEY T，REED P A S，STARINK M J. Short Crack initiation and growth at 600℃in notched specimens of Inconel 718［J］. Materials Science and Engineering:A，2003，340:139 －154.

［11］HUANG X Y，YU H C，XU M Q，et al. Experimental investigation on microcrack initiation process in nickel－based superalloy DAGH4169 ［J］. International Journal of Fatigue，2012，42:153 －164.

［12］NEWMAN J C. FASTRAN－ΙΙ —— a fatigue crack growth structural analysis program［R］. NASA TM 104159，1992.

［13］NEWMAN J C. A crack－closure model for predicting fatigue crack growth under aircraft spectrum loading［C］//CHANG J B，HUDSON，ed. Methods and Models for Predicting Fatigue Crack Growth under Random Loading.ASTM STP 748. 1989:53 －84.

［14］NEWMAN J C. A nonlinear fracture mechanics approach to the growth of small cracks ［R］. AGRAD－CP－328.1983.

［15］NEWMAN J C. A crack closure model for predicting fatigue crack growth under air craft spectrum loading［R］.ASTM STP 748. 1981:53 －84.

［16］NEWMAN J C. A crack opening stress equation for fatigue crack growth［J］. International Journal of Fracture，1984，24:R131 －R135.

［17］WU X R，NEWMAN J C，ZHAO W，et al. Small crack growth and fatigue life predictions for high－strength aluminum alloys:part Ι:experimental and fracture mechanics analysis［J］. Fatigue Fract Engng Mater Struct，1998，21:1289 －1306.

［18］ZERBST U，MADIA M，HELLMANN. An analytical fracture mechanics model for estimation of S-N curves of metallic alloys containing large second phase particles［J］. Engineering Fracture Mechanics，2012，82:115 －134.

［19］MURAKAMI Y. Metal fatigue:effects of small defects and nonmetallic inclusions ［M］. Oxford:Elsevier Science Ltd:2002.