一种基于特征子图的不确定图分类算法

刘 意，王 勇＊，尚学群

（1西北工业大学 理学院；2西北工业大学 计算机学院，陕西 西安710072）

图分类在化学、生物信息学、计算机科学等许多领域都有重要的研究和应用价值．例如，在生物和化学领域判断一种化合物是否有毒就是很常见的实例，其中分子化合物中原子构成图的顶点，原子键构成图的边，从大量有毒的分子化合物结构图中寻找频繁子图，这样的子图可以用来判断其他分子化合物是否有毒．目前，图分类的方法主要包括基于频繁子图的分类方法［1－4］和基于图核函数的分类方法［5－6］，它们在一定程度上解决了图分类问题．然而由于硬件条件、人为原因和环境等因素的影响，图结构中存在大量的不确定性，不确定图不同节点之间的联系是以一定概率存在的，因此不能简单地采用以往的分类方法来处理不确定图分类．而现实中的应用对不确定图的分类提出需求，例如，人类大脑不同区域功能之间联系就存在不确定性，通过对大脑区域结构图的分类，可以判断人是否患有某种脑部疾病，因此研究不确定图分类是很有必要的．基于上述原因，研究不确定图分类算法，这种算法也适用于确定图分类（确定图是特殊的不确定图）．先根据频繁子图构造特征子图［7］，然后由特征子图产生分类规则．本文在文献［2］构造分类模型的基础上，考虑不确定图的特点，采用以蕴含子图概率作为权重的方法，使分类模型可以适用于不确定图分类，同时提出AGF（Apriori for Graph Frequent Sets）频繁子图挖掘算法，将频繁子图挖掘问题转换为频繁项集挖掘问题，可以高效地发掘频繁子图．

1 构造特征子图

本文研究不确定图分类问题．算法的步骤是：首先采用AGF算法挖掘频繁子图，再从频繁子图集中筛选特征子图，最后通过特征子图生成分类规则．

1．1 挖掘频繁子图

在给出频繁子图挖掘算法之前，先通过定义引出子图期望支持度的计算公式．

定义1（不确定图） 一个不确定图G＝（V，E，p），其中V＝ ｛v1，v2，…vn｝表示顶点集，E⊆V×V表示边集，p：E→ （0，1］表示边上的概率．相应的，确定图表示为G＝（V，E）．不确定图集合表示为D＝｛G1，G2，…Gn｝，D可以分为D＋和D－，分别为不确定图的正例和负例集合．

假设不确定图的各个边是独立的，一个不确定图G包含某个确定图G的概率为

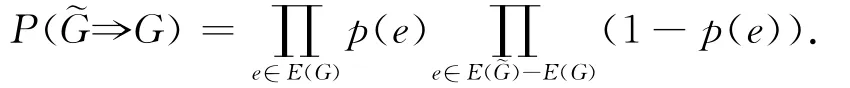
定义2（子图） 子图g＝ （V′，E′）为某个确定图G＝（V，E）的子图当且仅当V′⊆V且E′⊆E，记为g⊆G．通常情况下，子图是针对确定图而言的概念．

对于不确定图，g为G的子图用概率表示为

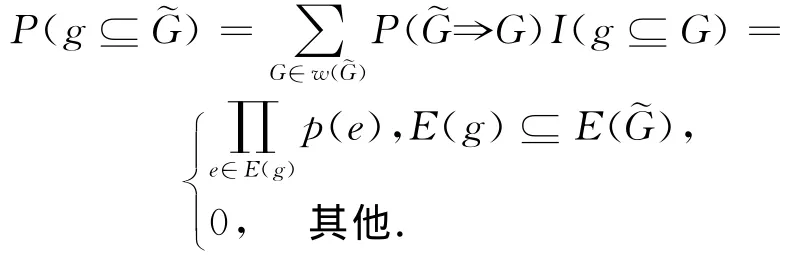
其中

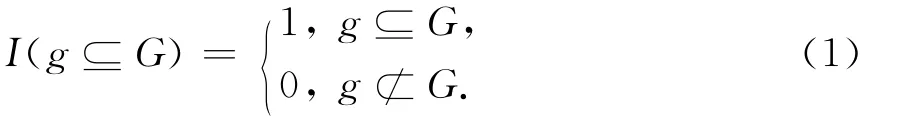
可以计算出子图g在不确定图集合D中的期望支持度：

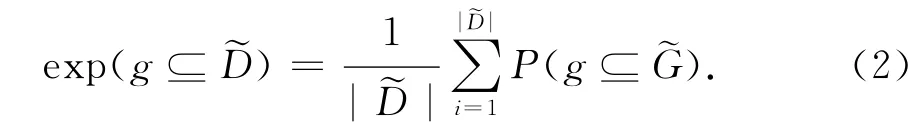
公式（2）可以用来计算子图的期望支持度．给定最小支持度min＿sup，当子图g满足exp（g⊆D）＞min＿sup，则g为频繁子图，记为fre＿g．

定理1 给定不确定图集合D，子图在D中的期望支持度满足Apriori性质，即对任意的子图g和g′，若g是g′的子图，那么exp（g⊆D）≥exp（g′⊆D）．

以定理1为理论依据，挖掘频繁子图可以采用Apriori算法中的剪枝方法．

由于子图的连接方式有很多种，候选子图产生问题一直是频繁子图挖掘的难点．近年来，有关频繁子图挖掘算法一直将注意力集中在如何有效地生成候选子图［8－10］．将频繁子图的挖掘转换为频繁项集的挖掘，可以简化繁琐的过程，从而节省时间．

下面介绍AGF算法．假设每个不确定图拥有相同的顶点及顶点标号，也就是说，不同的不确定图的差异在于两个顶点之间的边存在性以及存在的概率．这样的假设是有意义的，比如对人脑结构的分析，每个人的脑结构都是一样的，而人脑不同部分之间的联系是不确定的．

通过对图的顶点个数和标号的限定，把频繁子图挖掘转化为传统的频繁项集的挖掘，具体做法如下：对于每一个不确定图（图1），可以用其邻接矩阵来表示．这样，每个边就用两个点表示，进而每个子图可以用字符串表示．下面举例说明字符串的表示：图1中，v0v1表示边e1（下标由小到大），e1e2e3表示整个不确定图（下标由小到大），从而v0v1v0v2v2v3也表示整个图．这样，每个图以及每个子图，采用上

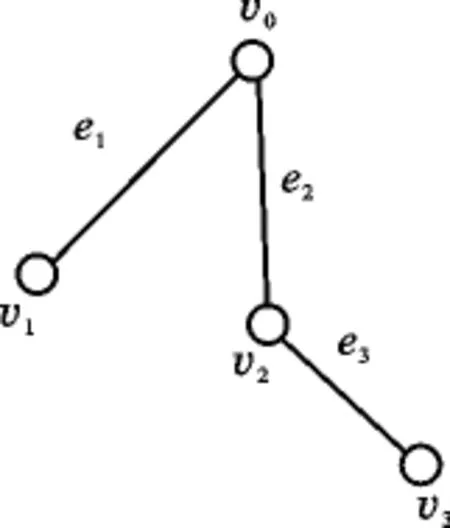
图1 某不确定图Fig．1 An uncertain graph

在使用Apriori算法时，有一点需要注意，由于子图都是联通的，所以，在计算频繁二项集时，需要简单的处理：两个频繁一项集合并时，必须有公共顶点．比如v0v1和v2v3就不能合并．可以发现，仅仅在处理二项集时，才需要这样的处理．把不确定图集合D＋和D－中的频繁子图集合记为F＋和F－．

以正例集合为例，具体算法如下：

输入：D＋／／由带有顶点标号的图数据集合正例转换来的字符串；min＿sup／／最小支持度

输出：F＋／／正例频繁图数据集合

1．2 构造特征子图

并不是每个频繁子图对分类都有意义，比如当某个子图g在两个不确定图集合中都频繁但支持度相差很小，那么它的支持度比就很小，认为它不是特征子图．

定义3（特征子图） 对于D中的某个频繁子图fre＿g，其支持度为sup1，fre＿g在另一个不确定图集合1中的支持度为sup 2．可以计算支持度比：

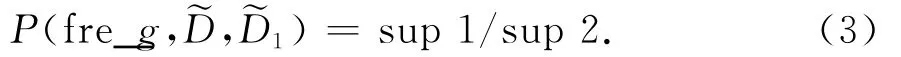
给定最小支持度比min＿p，当P（fre＿g，D，D1）≥min＿p，认为fre＿g为特征子图，记为fea＿g．

构造特征子图就是对频繁子图正例集合F＋和负例集合F－的筛选，去除其中的非特征子图，从而得到特征子图集合．分别记为F＋和F－．

需要注意的是，存在这样一种可能，对于一个被测不确定图G，某个特征子图的真子集仍然是特征子图．那么在利用特征子图分类时，这个子集作为分类特征的意义不大，应该筛选掉．即对于被测图G，g1和g2都是特征子图，若g1⊂g2，筛选掉g1．

2 具体分类实现

学习步．对于不确定图集合D＋和D－，首先通过AGF算法分别得到频繁子图集合F＋和F－，再由公式（3）和最小支持度比筛选出特征子图集合F＋和F－．

与确定图不同，不确定图蕴含某个子图是以一定概率存在的，在利用特征子图对不确定图分类的过程中，需要将概率考虑进去，即在文献［2］利用特征子图构造模型的基础上，增加概率作为权重．

对于一个待判断的不确定图G，进行如下操作：

步骤1 分别对F＋和F－中的每个成员fea＿gi与待判断图G做子图匹配，对于不确定图来说，蕴含某个子图的概率可以利用公式（1）计算得到P（fea＿gi⊆G）．

步骤2 由公式（3）可知，当正例集合D1中的某个特征子图fea＿gi在负例集合D2中越频繁，则P（fea＿gi，D1，D2）越 小，在D2中越不频繁，则P（fea＿gi，D1，D2）越大，即特征越明显．对不确定图G，计算得分数s．

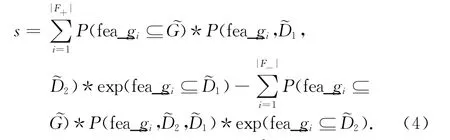
步骤3 根据得分数s，对G分类．如果s＞0，不确定图G归为D1；否则，不确定图G归为D2．

3 实验结果与分析

数据集来自于LONI网站的对老年痴呆患者大脑结构的观察，可以从相关网站（http∥adni．loni．ucla．edu）申请得到．数据集分为正例和负例两类，正例为老年痴呆患者的脑部结构图，负例为正常人的脑部结构图，每类各200个实例，其中100个用来学习，100个用来测试．如图2所示，两个图分别表示正例和负例的大脑结构区域联系图，其中点代表大脑结构中的各个区域，加权边代表各个区域以一定的概率存在相互的联系．不同的实例具有相同的顶点个数以及顶点位置，这也正好符合前面做的假设．在实验开始前需要用邻接矩阵表示结构图．

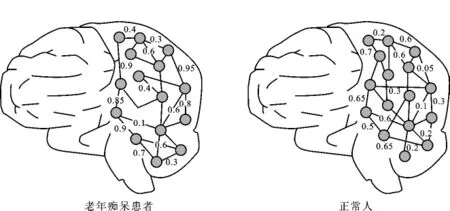
图2 老年痴呆患者和正常人的脑部结构图Fig．2 An example figure of an Alzheimer patient and a healthy people

通过实验观察，实验结果的准确率是由最小支持度min＿sup和最小支持度比min＿p来控制的，且在本实验中主要由min＿sup控制，这和实验数据的特点有关．

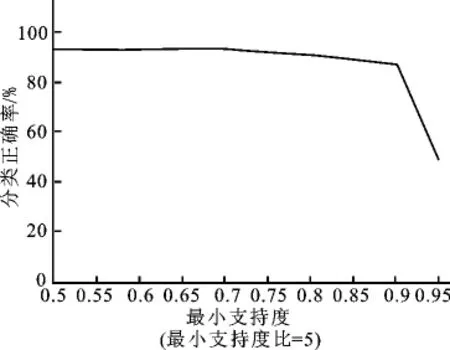
图3 最小支持度与分类正确率关系图Fig．3 The diagram of the smallest support and the accuracy of classification

图3和图4都可以说明在min＿sup设置合适时，比如0．8，该算法具有良好的分类正确率．当min＿sup取值过大，会因为过滤掉许多本身具有良好分类能力的子图而影响分类能力，当min＿sup取值过小，则影响算法的效率．从图3可以看出，当min＿sup＝0．95时，正确率非常低，而随着min＿sup的减小，正确率迅速增高并且在min＿sup＝0．8后趋于平缓，其后基本稳定在90%以上．当min＿sup低于0．5后，实验不予考虑，因为已经不属于频繁子图的范畴．从图4也同样可以看出，随着min＿sup的

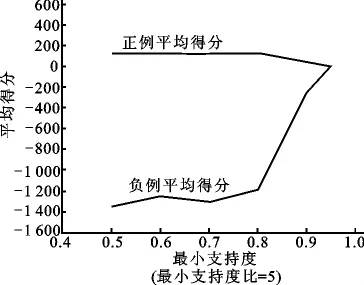
图4 最小支持度与平均得分的关系图Fig．4 The diagram of the smallest support and the score

逐渐降低，正例平均得分逐渐增高且在min＿sup＝0．8后趋于平缓，负例平均得分逐渐降低且在min＿sup＝0．8后趋于平缓，随着min＿sup的降低，二者得分之差越来越大，可以理解为算法将正负例区分的越来越明显．

4 结语

研究了一种新的频繁子图挖掘算法——AGF算法．通过论证该算法具有高效性，同时也具有局限性，即研究对象必须为同构图．在利用AGF算法高效生成频繁子图的前提下，提出针对不确定图的分类算法．通过对实验结果的观察及分析，可以得出：在最小支持度min＿sup和最小支持度比min＿p设置合适的情况下，算法对不确定图具有良好的分类能力．

［1］Deshpande M，Kuramochi M，Karypis G．Frequent substructure based approaches for classifying chemical compounds［J］．IEEE Transactions on Knowledge and Data Engineering，2005，17（8）：1036－1050．

［2］刘勇，李建中，朱敬华．一种新的基于频繁闭显露模式的图分类方法［J］．计算机研究与发展，2007，44（7）：1169－1176．

［3］王桂娟，印鉴，詹卫许．一种新的基于嵌入集的图分类方法［J］．计算机研究与发展，2012，49（11）：2311－2319．

［4］Liu Yang，Wu Bin，Wang Hongxu．BPGM：A big graph mining tool［J］．Tsinghua Science and Technology，2014，19（1）：33－38．

［5］Horvath T，Garner T，Wrobel S．Cyclic pattern kernels for predictive graph mining［C］／／Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining．Seattle：Association for Computing Machinery，2004：158－167．

［6］肖港松，陈晓云．基于代价敏感的图分类算法［J］．福州大学学报：自然科学版，2012，40（3）：316－321．

［7］Cheng Hong，Yan Xifeng，Han Jiawei．Discriminative frequent pattern analysis for effective classification［C］／／IEEE 23rd International Conference on Data Enginering．Istanbul：IEEE Computer Society，2007：716－725．

［8］陈立宁，罗可．Apriori算法用于频繁子图挖掘的改进方法［J］．计算机科学与应用，2011，47（10）：113－117．

［9］高琳，杨建业，覃桂敏．动态网络模式挖掘方法及其应用［J］．软件学报，2013，24（9）：2042－2061．

［10］邹兆年，李建中，高宏．从不确定图中挖掘频繁子图模式［J］．软件学报，2009，20（11）：2965－2976．