超－π－Brauer特征标理论

钟艳林，郑秉文

(1.闽南理工学院;2.北华大学)

0 引言

对于Brauer特征标，有人建立这样的理论:设G是有限群，p为一个固定的素数，G0为G的p－正则元的集合，而cl(G0)表示G的p－正则元所在的共轭类的集合.IBr(G)表示G的不可约p－Brauer特征标的集合.

假设IBr(G)被划分为族Y，并且假定对每一个，选择一个非零Brauer特征标θY，其不可约Brauer成分都在Y中.若可以找到G0的一个划分为K的族使得Brauer特征标θY在K∈K上取常值，并且|Y|=|K|.还要求{1}∈K.在这种情况下，称θY为G的超 －Brauer特征标.

1 新的一节

对于π－Brauer特征标是否也可以建立类似的理论呢?在该文中，将讨论关于π－Brauer特征标的一些结论.设G为π－可分群，G*为G的π－正则元的集合，cl(G*)表示G的π－正则类的集合.Iπ(G)表示G的不可约π－Brauer特征标的集合.首先来看几个引理.

定义1 设π是一个素数集合，如果|G|的每个素因子均在π中，称有限群G为π群［1］.

定义2 称有限群G为π群，如果存在G的一个正规群列G=N0≥N1≥N2≥…≥Nr=1，使 Ni/Ni+1为 π 群，i=0，1，2，…，r－ 1.

引理3 设χ∈Bπ(G)，G为π －可分群，则Oπ'(G)⊆ kerχ.

引理4 设G为π－可分群.对每个子集Y∈Y，θY是一个非的π－Brauer特征标，它的不可约成分都在Y中.假如|Y|=|K|，并且θY在集合K∈K中取常值.那么下面结论等价:

(1)子集{1}∈K.

(2)每个π－Brauer特征标θY是δY的一个倍数..

(3)任意的φ∈I*(G)是某一个π－Brauer特征标θY的一个成分.

证明 注意到Iπ(G)是π－正则共轭类函数空间的一组基底并且子集Y∈Y是无交的，因此θY是线性无关的.设S是在子集K∈K上取常值的复值函数空间.因为所有的θY属于S并且|Y|=|K|，故{θY|Y∈Y}是空间S的一组基底［2］.

假设(1)成立，注意到ρ*在K的所有成员上去常值，于是存在适当的复数aY使得

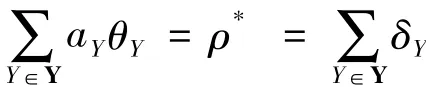
因为Iπ(G)是线性无关的，且Y∈Y是两两无交的，从而对所有的Y∈Y，aYθY=δY，于是(2)得证.而且，通过比较次数还可以得到aY是一个有理数.

因δY是非零的π－Brauer特征标，由(2)可立刻推(3).

现假定(3)，由此来证明(1).设K∈K包含1，又设g∈K.由于每个π－Brauer特征标θY在K上取常值，于是θY(g)=θY(1).注意到Iπ(G)={ψ*| ψ*∈ Bπ'(G)}. 于是 θY=，其中aψ是一个正整数.因为每个φ∈Iπ(G)是π－Brauer特征标θY的一个成分，于是g∈ker(φ)对所有的ψ∈Bπ'(G)都成立.由G为 π － 可分群可得g=1［3］.

引理5 设G为π－可分群，则σ∈Aut(C)置换作用在集合Bπ″(G)上.特别地，它置换作用在 Iπ(G)上.

证明 σ以χσ(g)=χ(g)σ的方式作用在Irr(G)上，其中σ∈Aut(G)and χ∈Irr(G).设χ∈ Bπ'(G)，(W，γ)∈ nuc(χ).不难证明，对任意的σ∈Aut(C)，(W，γσ)∈nuc(χσ)［4］.因为γ是π'－特殊的，所以γσ是π'－特殊的，进而χσ∈Bπ'(G).命题得证.

定理6 设G为π－可分群，K与Y分别为G*和Iπ(G)的划分，且假定π－Brauer特征标δY在K∈K上取常值，其中Y∈Y，则|Y|≤|K|.如果 |Y|=|K|，则有

(a)π －Brauer特征标集合{δY|}Y∈Y生成一个在K的成员上取常值的定义在G*上的复值函数空间.

(b)划分Y决定K，并且K是唯一最粗糙的与Y相谐调的G*的划分.特别地，K的成员是π－正则共轭类的并.

(c)K的某个成员恰由G的单位元组成，而Y的某个成员恰由G的主π－Brauer特征标组成.

(d)如果r是一个与|G|π'互素的正整数并且g∈G*，则映射g→gr诱导出K上的一个置换.

(e)若划分K也唯一确定Y，则复数域C的每一个自同构诱导出Y上的一个置换.

证明 用V表示在K∈K取常值的复值函数空间，则

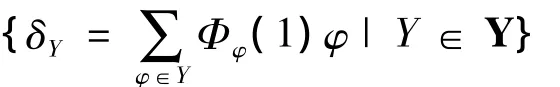
是V的一个线性无关子集.因为dim(V)=|K|，所以|Y≤|K||.假定|Y=|K||.由此得出{δY|Y∈Y}成为V的基，从而(a)的证明完成.

现在，证明(b).用K0表示G*的唯一最粗糙的与Y相谐调的划分.换句话说，在G*上定义关系 ～，u～v当且仅当对所有的Y∈Y，δY(u)=δY(v).于是K0的成员就是在此关系下的等价类.(特别地，如果u，v∈G*在G中共轭，则u～v，从而K0的成员是正则类的并.)因K的每个成员包含在K0的某个成员中，故|K0|≤|K|=|Y|.而由第一段的证明得出，|K0|≥|Y|，于是，|K0|=|Y|=|K|，K=K0.(b)的证明完成.

如果r是与|G|π'互素的正整数，则存在整数 s，t∈Z 使得rs+|G|π't=1.假设gr=hr，其中 g，h ∈ G*，则 g=grs+|G|π't=hrs+|G|π't=h.由此推得映射g→gr定义了G*的一个置换.如果把这个映射应用到K的成员上，则可得G*的一个新的划分L.因为(r，|G|π')=1，再由Galois理论，存在一个Galois自同构σ∈Gal(Q|G|π'/Q)使得对所有的φ∈Iπ(G)和g∈G*均有φ(gr)= φ(g)σ［5］.因此，若K∈K且Y∈Y，则当g跑遍K时，均可得到δY(gr)=δY(g)σ是常值.所以π－Brauer特征标δY在L的成员上取常值.因|L|=|K|=|Y|故由(b)得到L=K，从而(d)成立.

假设σ是复数域C的一个自同构.根据引理5可知，σ置换Iπ(G).将σ作用在Y的每一个成员上，从而得到Iπ(G)的一个新的划分Z.如果z∈Z，则存在y∈Y使得z=Yσ.注意到δz=(δY)σ在 K∈ K上取常值.现在，因 |Z|=|Y|=|K|且K唯一确定Y，故Z=Y，从而σ在Y上诱导一个置换.从而(e)成立.

最后给出两个具有非平凡超－π－Brauer特征标理论的π－可分群的例子.

例1 Let G=C3×D70，D70是70阶的二面体群.容易知道 G是可解群.取π ={5，7}.使GAP［6］，G 的 π － Brauer特征标表见表1.

表1 G的π－Brauev特征标表

Iπ(G)的分划 Y 是{{φ2}，{φ2}，{φ3，φ4}，{φ5，φ6}}，对应的超 － π － 正则类是{{1}，{2G}，{，}，{，}}. 此外对应的超 － π －Brauer 特 征 标 是 δ{φ1}=35φ1，δ{φ2}=35φ2，δ{φ3，φ4}=35φ3+35φ4，δ{φ5，φ6}=35φ5+35φ6.

例2 Let G=C77×A5.取π =(7，11).那么G是π－可分群.使用GAP，G的π－Brauer特征标表见表2.

表2 使用GAP，G的π－Brauer特征标表

G的超 － π － 正则类是{{1}，{2G}，{3G}，{，.}}，超 － π － Brauer特征标是 δ{φ1}=77φ1，δ{φ2，φ3}=231φ2+231φ3，δ{φ4}=308φ4，δ{φ5}=385φ5.

［1］ 徐明曜.有限群导引:第二版.北京:科学出版社，1999.

［2］ Chen X Y，Zeng J W.Super－Brauer characters and superregular classes.Monatsh Math，2011，163:15 －23.

［3］ Cossey J P，Lewis M L，Navarro G.The number of lifts of a Brauer character with a normal vertex.J Algebra，2011，328:484－487.

［4］ Liu Y J，Song X L.A note on degrees of irreducible －Brauer characters.Arch Math(Basel)，2008(3):199 －204.

［5］ Navarro G.Nilpotent Characters.Pacific J Math，1995，169:343－351.

［6］ The Gap Group，GAP:Groups，Algorithms，and Programming，Version 4.12，2009，http://www.gap－system.org.