从涨落的角度讨论三种系综分布之间的关系*

呼和满都拉，冀文慧，杨洪涛，胡晓颖

(集宁师范学院)

0 引言

热力学统计物理学的研究对象从少量个体变为由大量个体组成的群体，导致规律性质和研究方法的根本变化，大量粒子系统所遵循的统计规律是不能归结为力学规律的.统计物理是由微观到宏观的桥梁，它为各种宏观理论提供依据，已经成为气体、液体、固体和等离子体理论的基础，并在化学和生物学的研究中发挥作用.气体动理论(曾称气体分子运动论)是早期的统计理论.它揭示了气体的压强、温度、内能等宏观量的微观本质，并给出了它们与相应的微观量平均值之间的关系.平均自由程公式的推导，气体分子速率或速度分布律的建立，能量均分定理的给出，以及有关数据的得出，使人们对平衡态下理想气体分子的热运动、碰撞、能量分配等等有了清晰的物理图像和定量的了解，同时也显示了概率、统计分布等对统计理论的特殊重要性.而在统计物理中对系综的研究尤为重要.

统计理论系综是平衡态的普遍理论，它适用于任何多粒子系统，包括粒子之间的相互作用尤其重要作用的情形，例如稠密气体、液体、相变和临界现象等.最早是由波尔兹曼提出的.以后，Gibbs建立了经典统计系综的完整的理论表述.在量子力学建立后，经过泡利、冯·诺依曼、狄拉克、克拉莫兹和朗道等人的努力，建立起以量子力学为基础的统计系综理论.

1 统计系综理论的讨论

当我们的研究对象从单个或少数粒子变成由大量粒子和准粒子组成的，具有大量随机变化自由度的宏观系统的.由于大量随机自由度的存在，用纯粹的力学方法已不能解决问题了，应运产生了新的研究方法——系综理论.系综是大量系统(N个)的集合.系统中的每个系统和被研究系统具有完全相同的结构，受到完全相同的宏观约束，但可能处于不同的微观态.系综是统计物理中假想的工具，而不是实际的客体，实际的客体是组成系综的单元——系统.根据不同的宏观条件，我们将常见的稳定系统分为三种系统:由孤立系统组成的微正则系统;由恒温封闭系统组成的正则系综和由开放系统组成的巨正则系综.在统计系综中，三种系综分布存在紧密的关系，微正则分布是作为基本假设提出的，正则分布和巨正则分布是在这一假设基础上导出的.这三种分布所对应的系综宏观条件各不相同，但在确定系统的统计性质时，这三种分布完全等效.在原理上，我们是以微正则系综为出发点.据此推导出正则系综和巨正则系综.虽然这三种系综所描述的系统，其宏观条件有所不同，但在处理实际问题时，这种差异并不会表现出来.其结论都是相同的.或者说，三种统计系综在处理问题上具有等效性.这种等效性源于实际系统都含有大量粒子，由系综平均值求出的宏观量相对涨落非常小，因此系综分布函数存在一个很大的峰，这个峰值处几乎包括了全部的概率.

1.1 微正则分布

微正则系综是指系综里的每个体系具有相同的能量(通常每个体系的粒子数和体积也是相同的).

其物理意义是:经典微正则系综中所有系统的微观态代表点，稳定而均匀地分布在空间的能量壳层内.

1.2 正则分布

正则分布对应的是正则系综，它说明系综里的每个体系都可以和其他体系交换能量(每个体系的粒子数和体积仍然是固定且相同的)，但是系综里所有体系的能量总和是固定的.系综内各体系有相同的温度.系统与大热源接触且处于平衡，具有确定的粒子数N，温度T，体积V.若系统有Nr个自由度.

从物理意义上讲，配分函数是系统的有效状态和;从数学上讲，它是为了方便而引入的一个生成函数.通过系统的能量函数来得到系统的配分函数是利用系综理论处理实际问题的关键.因为有了配分函数就可以通过热力学公式得到该系统的热力学性质.

1.3 巨正则分布

正则系综的推广，每个体系都可以和其他体系交换能量和粒子，但系综内各体系的能量总和以及粒子数总和都是固定的.(系综内各体系的体积相同.)系综内各个体系有相同的温度和化学势.当系统与热源，粒子源相接触，其体积V，温度T以及化学势具有确定值时.

这三种分布所对应的系综宏观条件各不相同，但在确定系统的统计性质时，这三种分布是完全等效的.

2 三种系综的涨落

在热力学统计物理学中的涨落有很多，但是上面三种系综的涨落主要有两个方面，下面分别从能量涨落，粒子数涨落分析讨论三个系综的关系:

2.1 能量涨落

涨落是大量微观粒子的一种统计平均行为，是大量微观粒子如分子、原子、电子等无规则热运动的结果.下面就具体介绍能量的涨落.能量张落的定义式是:

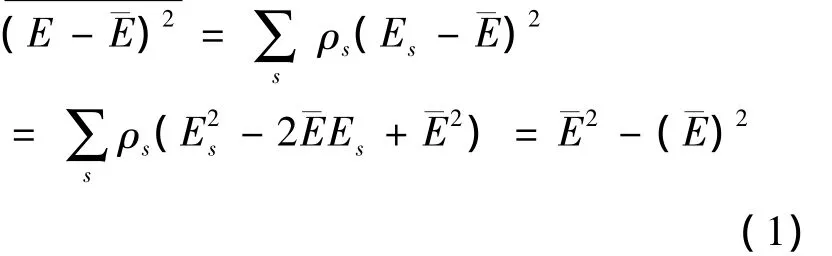
正则分布

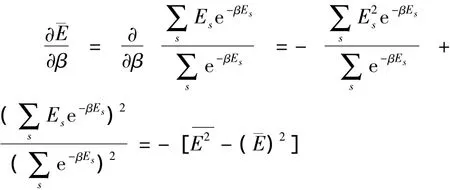
所以

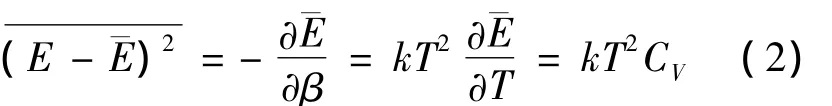
能量的相对涨落为:

由此，说明正则系统与微正则系统是等价的，微正则系综处于孤立系中，能量E有确定值，因此能量涨落为0，所以微正则分布是正则分布忽略能量E的涨落的结果.

通过以上两例说明:正则分布能量的相对涨落与N－1成正比，对于宏观系统来说，能量的相对涨落是完全可忽略的.能量E与¯E有较大的偏

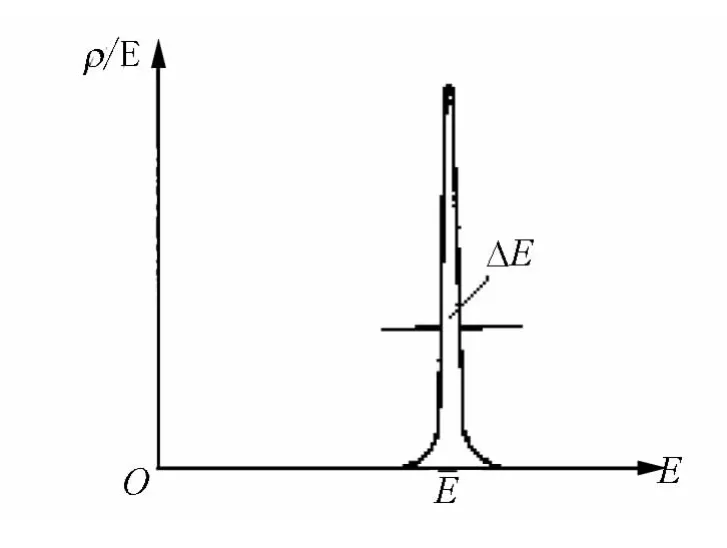
图1

2.2 粒子数涨落

巨正则分布中的粒子数的绝对涨落:

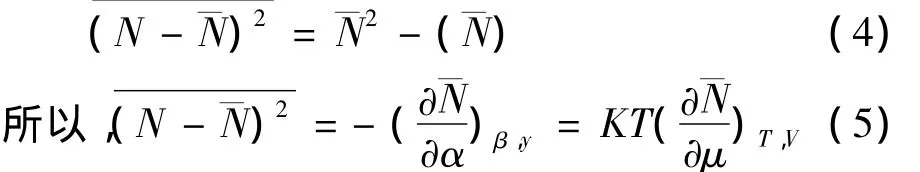
粒子数的相对涨落为:

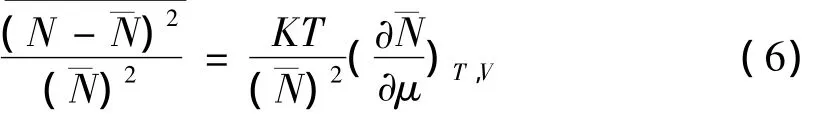
还可用另一种形式表示:

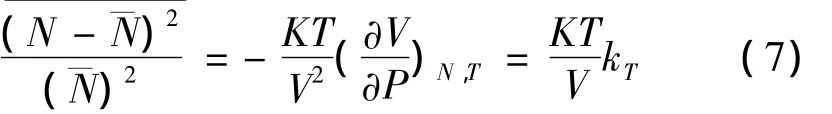
下面分别以单、双原子为例讨论:

(1)单原子分子理想气体

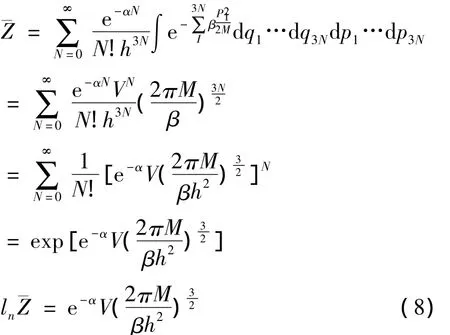
系统的粒子数为:

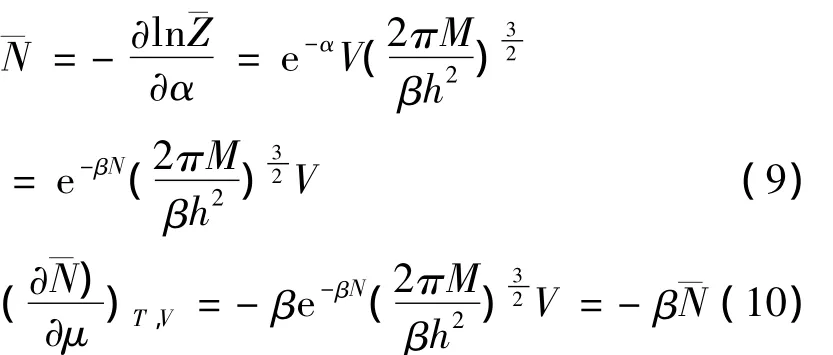
粒子数的相对涨落:

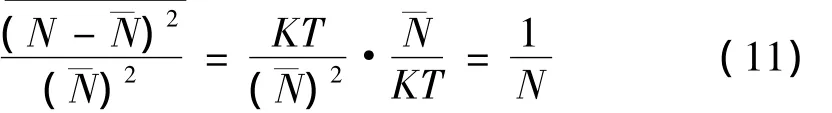
(2)以双原子分子为例:

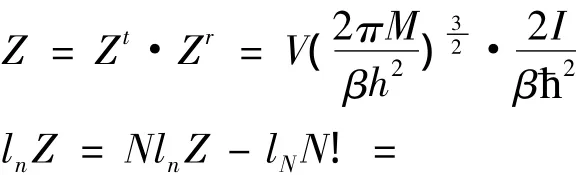
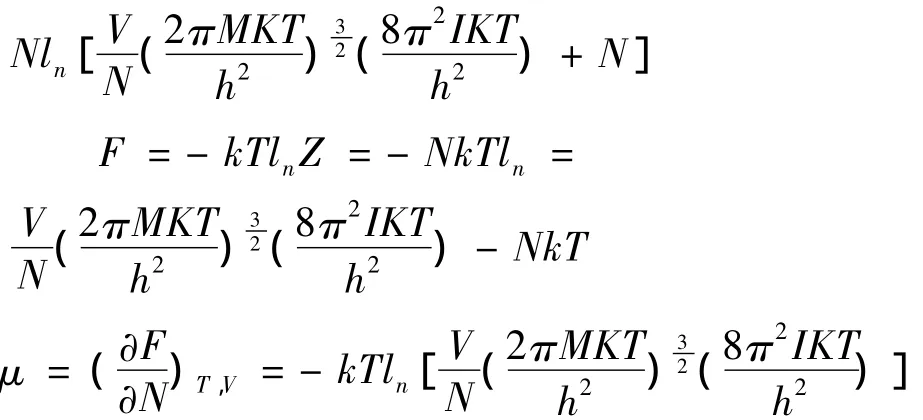
将此式代入(7)并将pV=¯NKT代入(7)得:

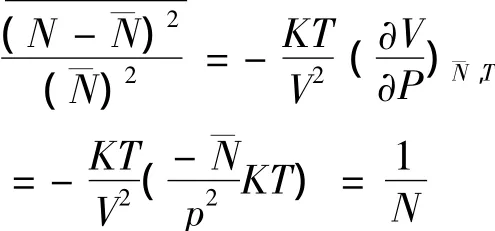
通过以上例子说明:粒子数的相对涨落与N－1成正比，对于宏观系统粒子数的相对涨落可忽略.

2.3 正则分布的能量涨落

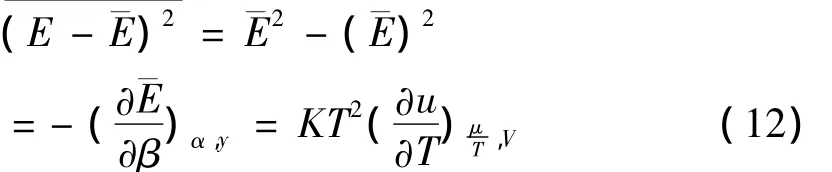
因为

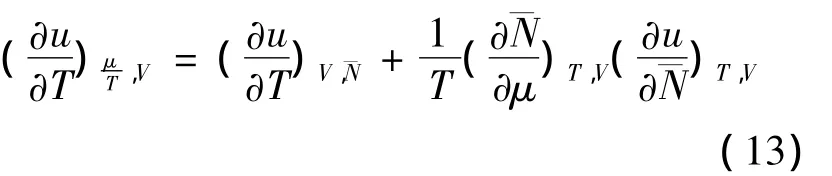
所以

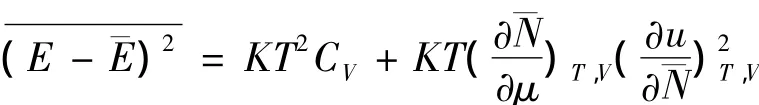
说明:正则系综的能量涨落是巨正则系综的能量涨落忽略粒子数N的能量涨落的结果.

3 结束语

综上所述，三种统计系综的关系是:它们是等价的，但应用的广泛程度不同，方便应用的条件不同.三种系综等价的含义为:虽然组成三种系综的系统所处的宏观条件有原则上的区别，但在热力学极限下用三种系综计算同一个宏观系统的热力学量时，会得到相同的结果.也就是，我们可以不管系统所处的实际系统，按照方便，采用任何一种系综进行计算，结果都是相同的.

三种系综是等价的是因为对于微观系统，能量的相对涨落是极小的，所以正则系综和微正则系综是等价的，用微正则分布和正则分布求得的热力学量实际上相同.用这两种分布求热力学量实质上相当于选取不同的特性函数，即分别选取自变量为(N，V，E)的内能U和自变量为(N，V，T)的自由能F(N，V，T)为特性函数.对于微观系统，由于粒子数的相对涨落是很小的，因而正则分布和巨正则分布等价，即使在粒子数相对涨落很大的情形，巨正则分布与正则分布仍将给出相同的热力学信息.用巨正则分布与用正则分布求热力学量相当于选取不同的特性函数，即分别选取巨热力学势Ω(T，μ，V)和自由能F(N，V，T)为特性函数.实际上，对粒子数相对涨落很大的情形，使用巨正则分布比较方便.

直接应用微正则系综往往比较困难，由于计算Ω(E，N，V)必须满足能量守恒和粒子数守恒两个约束条件，而计算Z(T，V，N)解除了对能量守恒的约束而变得比较容易.虽然理论上微正则分布与正则分布等价，但实际上正则分布比微正则分布应用更广泛，也方便得多.巨正则系综的巨配分函数Z(T，V，μ)的计算因同时消除了能量守恒和粒子数守恒的约束而变得更容易.

总之，从理论角度考虑，微正则系综是系综理论的基础，正则分布和巨正则分布是由微正则分布导出的;在应用上，三种系综是等价的，实际上，巨正则系综由于其巨配分函数计算最简单而应用最广.

［1］ 汪志成.热力学·统计物理:第四版［M］.北京:高等教育出版社，2006.

［2］ 缪胜清.热力学统计物理习题选解［M］.合肥:安徽大学出版社，1998.

［3］ 苏汝铿.统计物理学:第二版［M］.北京:高等教育出版社，2006.

［4］ 郑瑞伦.热力学·统计物理学［M］.重庆:西南师范大学学报，2003.

［5］ 苏安.热学与热力学统计物理［M］.教育与职业，2008.