具有攻击角约束的非奇异终端滑模导引律设计

周慧波，宋申民，刘海坤

（1. 哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001；2. 哈尔滨师范大学 数学科学学院，哈尔滨 150009）

具有攻击角约束的非奇异终端滑模导引律设计

周慧波1,2，宋申民1，刘海坤2

（1. 哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001；2. 哈尔滨师范大学 数学科学学院，哈尔滨 150009）

为了满足导弹拦截高速大机动目标时高精度制导的需求，首先对二维平面内的弹目相对运动方程进行状态扩张，对于影响制导性能的目标总扰动采用了扩张状态观测器的方法进行动态补偿。然后在非奇异终端滑模面的基础上选取了两种滑模趋近律，设计了两种具有攻击角约束的非奇异终端滑模导引律。最后数值仿真结果表明，在观测器对扩张系统状态进行实时有效估计的前提下，针对不同的期望视线角和目标机动方式，所设计的两种导引律在满足期望的性能要求的同时，可实现导弹对目标的高精度快速打击。

扩张状态观测器；非奇异终端滑模面；趋近律；有限时间；导引律

随着精确制导武器的不断发展，在制导律设计中除了对脱靶量的要求外，在许多应用场合中还需要对制导末端的角度进行约束，以便使战斗部发挥最大效能，取得最佳毁伤效果[1]。因此有必要对带末端攻击角度约束要求的制导律进行深入研究，以满足这种特殊的制导任务。

自从Kim和Grider于1973年基于线性化模型，针对再入飞行器在垂直平面内提出一种最优攻击角度控制导引律以来[2]，一些学者针对不同的应用问题，提出了不同的攻击角度约束导引律[3-6]。文献[3]选取包含视线角和期望视线角两种信息的非奇异终端滑模面，设计了有限时间收敛的导引律。文献[4]运用滑模变结构的方法研究了导弹和目标之间三种拦截情况的攻击角约束问题，在导引律实现中采用饱和函数代替符号函数的方法减少滑模面的抖动。文献[5-6]采用终端滑模面研究了导弹制导和控制问题，但对于终端滑模面易出现奇异问题没有考虑。以上文献中将目标加速度机动作为未知的有界扰动进行估计，但这些界往往很难获得，若控制律中的这些数据取得太大，会影响控制效率；取得太小，将不能保证滑动模态的存在。因此，如何提高目标状态的估计精度，实现稳定、可靠而精确的目标跟踪具有十分重要的现实意义。

扩张状态观测器是一种新型的非线性状态观测器。通过把系统中的内外扰动扩张成新的一阶状态，再利用特定的非光滑非线性误差反馈，然后选择适当的观测器参数得到系统所有状态的观测值，其中也包括对象模型的不确定性和未知扰动的观测值。这非常适合于目标机动形式未知、只有量测输出和控制输入的机动目标加速度的估计问题[7-8]。本文运用此方法，对导弹制导系统中的目标机动进行实时估计。

传统滑模控制方法设计的线性滑模面，当系统状态到达滑模面后将渐近收敛到系统的平衡点，而不是有限时间收敛的，有限时间收敛在工程应用中更具有现实意义[9-10]。终端滑模控制方法实现了系统状态的有限时间收敛，获得了比传统滑模控制方法更好的收敛性能[11]。但终端滑模控制方法存在奇异问题，对此文献[12]提出一种克服奇异问题的非奇异终端滑模控制方法以改善控制性能。而为了提高到达阶段的动态品质和抑制传统滑模控制中的抖振，文献[13]利用传统幂次趋近律与指数趋近律的线性组合提出了一种快速幂次趋近律，在消弱滑模抖振的同时能改善状态远离滑模面时速度过小的劣势。

本文利用快速幂次趋近律和指数趋近律分别结合非奇异终端滑模面设计了具有攻击角约束的导引律，并和已设计的传统非奇异终端滑模导引律做比较。对于制导系统中未知的目标机动采用扩张状态观测器的方法进行动态补偿。仿真结果表明所设计导引律在收敛时间、抑制滑模抖动方面具有良好的性能。

1 问题描述

考虑如图1所示拦截平面内的弹目相对运动，导弹和目标均视为质点，并分别用 M,T表示，它们的连线称为视线。图 1中，r代表目标和导弹之间的相对距离，代表r对于时间的导数， Vt、 Vm分别代表目标和导弹速度，q代表视线角，代表q相对于时间的导数，分别代表目标和导弹的速度方向角。

假定导弹和目标的速度均为常值，攻击时刻攻角很小，则由图1可以导出如下微分方程描述：()

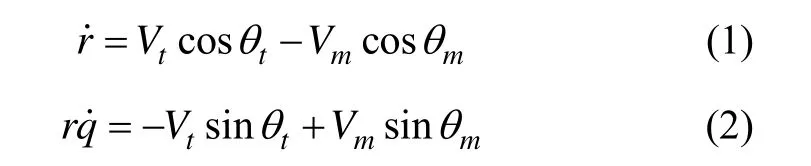
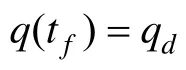
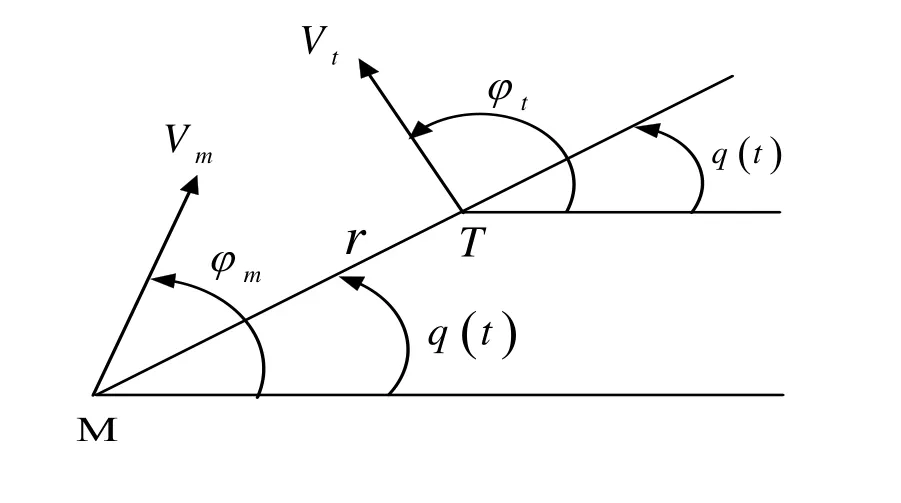
图1 导弹和目标相对运动关系Fig.1 Relative motion geometry of missile and target

在末制导过程中，由于受到导引头角跟踪系统功率、接收机过载等因素的限制，导引头存在最小作用距离 r0，当弹目相对距离小于或等于 r0时，制导回路断开，导弹在惯性作用下飞向目标，使得制导过程满足如下假设：

假设1[14]系统(2)中的时变参数 r(t)满足：

2 导引律的设计

为下文导引律证明方便，给出如下两个引理。

引理1[15]考虑非线性系统(4)：

引理2[13]考虑非线性系统(4)，如果存在连续、正定函数 V(t)满足如下的微分不等式：

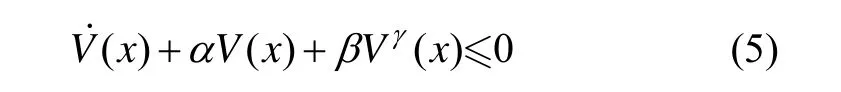
式中，α ,β ＞ 0，0 ＜ γ＜ 1均为常数，那么系统状态到达稳定点的时间T满足下面不等式：

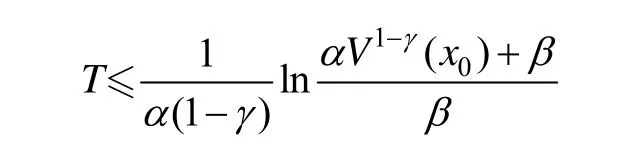
进一步，选取状态变量：

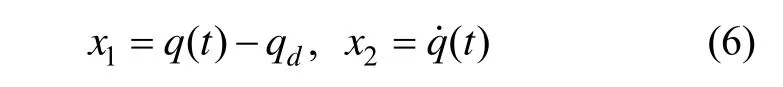
对式(6)求导，整理后可得视线角约束下制导状态方程为：

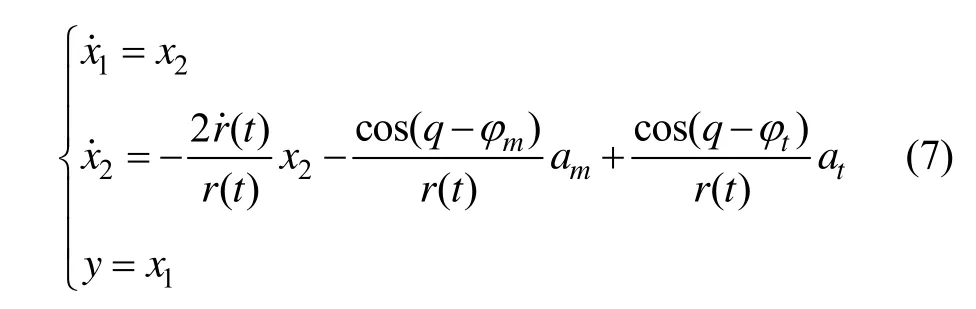
在实际制导过程中，如果目标进行机动，机动加速度 at是个很难获得的量，将其视为系统干扰，并在制导过程中是有界量，一般满足约束条件：

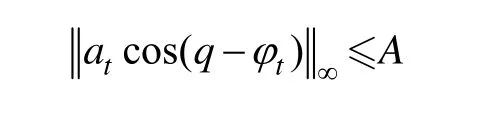
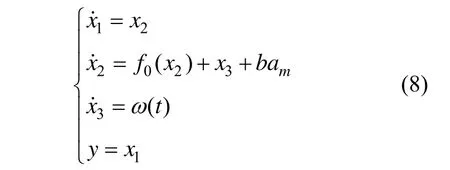
利用文献[16]的思想对系统(8)设计扩张状态观测器：

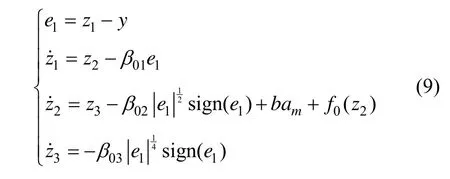
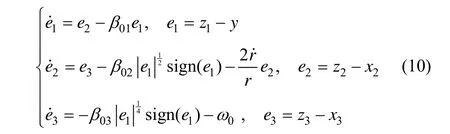
当系统(10)进入稳态时，方程右端全收敛于零。从而可以得到：

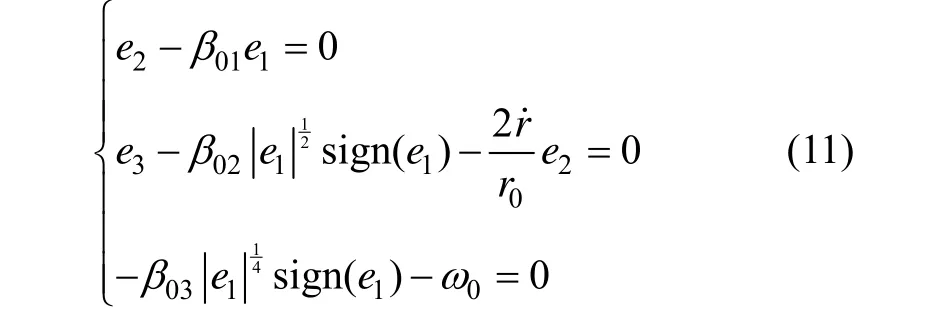
因此，由假设1可知，误差系统(11)的稳态误差为：

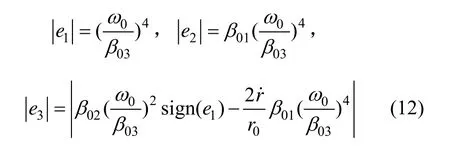
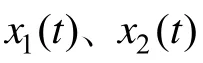
对系统(8)选取如下滑模面：

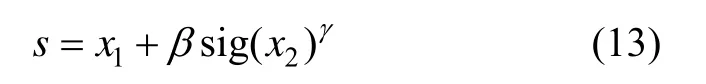
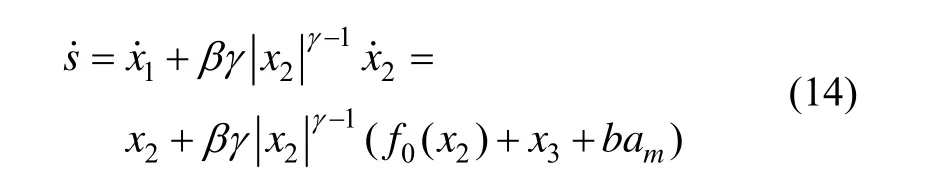
在滑模面方程(13)的基础上，分别选取不同的趋近律并设计相应的导引律。

2.1 指数趋近律

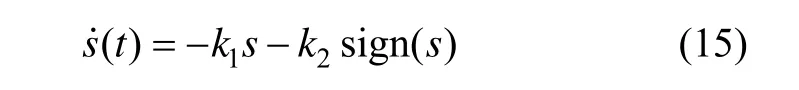
由式(14)结合式(15)，求得：

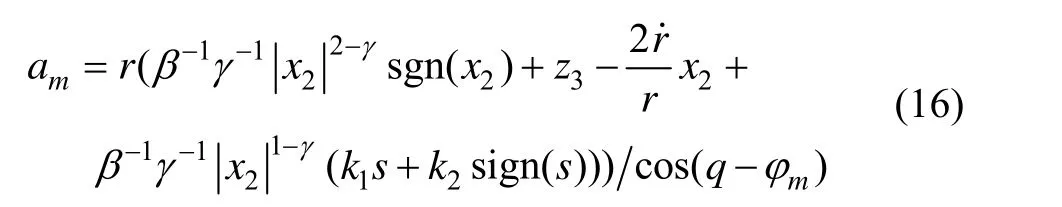
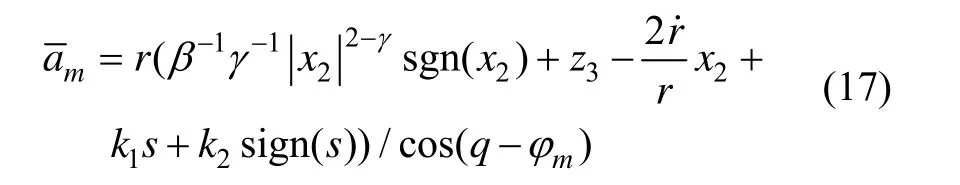
定理 1 对于系统(8)，在导引律(17)的作用下，系统(8)在有限时间内收敛到滑动模态 s= 0，并在有限时间内使得系统状态 x1,x2收敛到零，即视线角 q(t)收敛到 qd且视线角速率 q˙(t )收敛到零。

证明 选取Lyapunov函数：

对式(18)求导，并将式(14)和导引律(17)代入得：

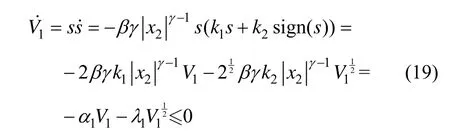
对式(20)求导，可得：

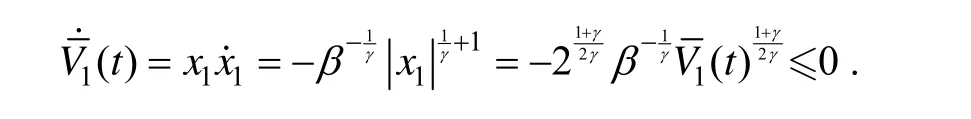
2.2 快速幂次趋近律

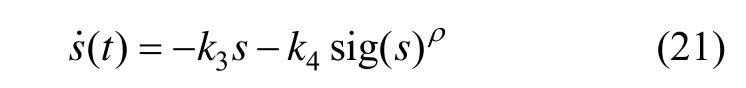
由式(14)结合式(21)，求得：

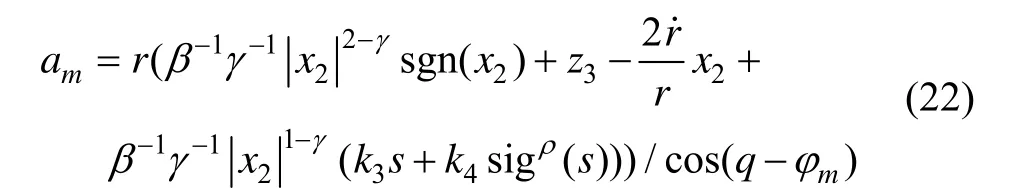
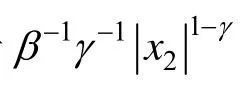
同样，由于因子的存在，为了避免系统的奇异现象，针对系统(8)设计导引律为：

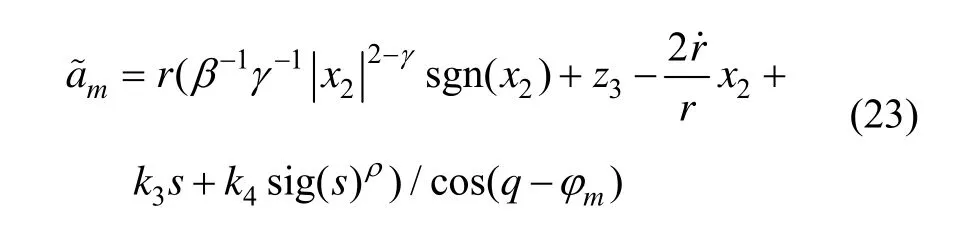
定理 2 对于系统(8)，在导引律(23)的作用下，系统(8)在有限时间内收敛到滑动模态 s= 0，并在有限时间内使得系统状态 x1,x2收敛到零，即视线角 q(t)收敛到 qd且视线角速率 q˙(t )收敛到零。

证明 选取Lyapunov函数：

对式(24)求导，并将式(14)和导引律(23)代入得到：

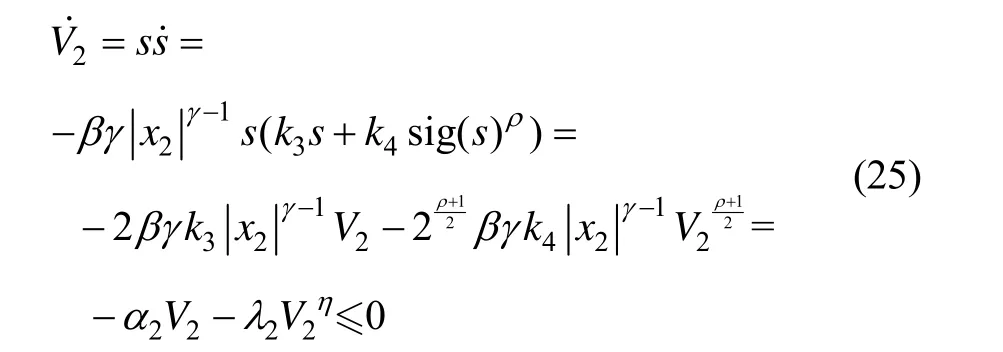
为了下文表述方便，称此导引律 a~m为基于快速幂次趋近律的非奇异终端滑模导引律，简便记为FNTSM。

关于非奇异终端滑模导引律的设计已有很多研究成果，文献[3]中设计的具有视线角约束的导引律为：

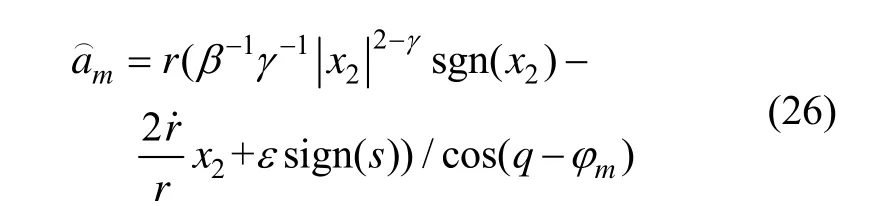
注1 由于导引律(26)中有因子“εs ign(s)”，其中的增益“ε” 包含了对目标机动的有界估计，选取过大过小都导致系统性能变差，而本文所设计基于趋近律的两种导引律，对于目标机动则使用扩张状态观测器的方法进行实时动态补偿，避免了估计目标机动的界。

注2 导引律ENTSM和NTSM方法中都含有“sign(s)”因子，为完全消除抖振，在仿真时将导引律中的符号函数用饱和函数sat(s)替代，其形式如下：

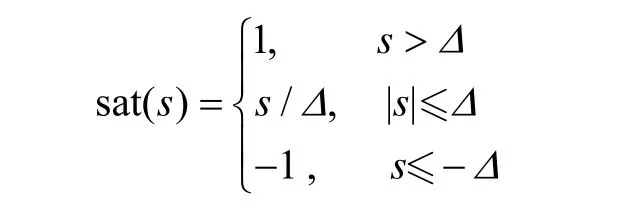
式中，Δ为边界层。

3 数值仿真分析

设某型导弹在某一高度上飞行，马赫数为3.5，音速为295.07m/s，目标的飞行速度为900 m/s，目标和导弹在铅垂面内运动。 设末制导初始时刻 t= 0，导弹在惯性系下的位置为 xm(0)= 0km ， ym(0)= 16km ，导弹初始弹道偏角为 φm(0)=50°，目标的初始位置为xt(0)=1 km， yt(0)=16.4 km，目标初始弹道偏角为φt(0)=60°。导引头中断寻的制导距离为 r0=100 m，之后导弹以惯性飞向目标。为了对比说明本文所设计导引律的鲁棒性，给出如下三种目标机动形式。

情况1： at=9gcos(πt /4)m/s2的余弦机动；

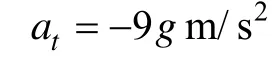
情况3： at= 9 gm/s2的常值机动。

目标做余弦机动时(情况 1)，相应的脱靶量和命中时间由表1给出，图2和图3分别给出相应的视线角速率、视线角、滑模面和导弹法向过载的变化曲线。由表 1可见，三种方法的脱靶量都较小。与导引律NTSM对比可知，本文设计的ENTSM 和FNTSM两种导引律的脱靶量更有优势。在导弹命中时间上， 在=20°时基本一致，但当 qd=30°时，NTSM的制导时间比前两种方法的时间长。

图2中(a)和(c)为 qd=20°时的视线角速率和期望视线角，图2(a)中可见三种方法都收敛到零，但NTSM提前发散且收敛时间较长，视线角速率曲线有震荡，这也导致图2(c)和图3(c)中相应的期望视线角和滑模面曲线的误差较大，而另两种方法的期望视线角和滑模面曲线的误差很小，特别是FNTSM方法比ENTSM方法更有优势。图2中(b)和(d)为 qd=30°时的视线角速率和期望视线角的变化曲线。在期望视线角增大的情况下，NTSM的视线角速率和视线角曲线振荡更剧烈，这也使得图3(b)和(d)中的过载长时间饱和，滑模面曲线也振荡到制导结束，导致制导性能变差。而由图2(b)和(d)可见，ENTSM和FNTSM方法仍然能使视线角速率曲线快速收敛到零，视线角曲线收敛到期望值。图3(b)和(d)中相应的过载曲线饱和时间很短并快速变小，滑模面曲线光滑无抖振且快速收敛到零。

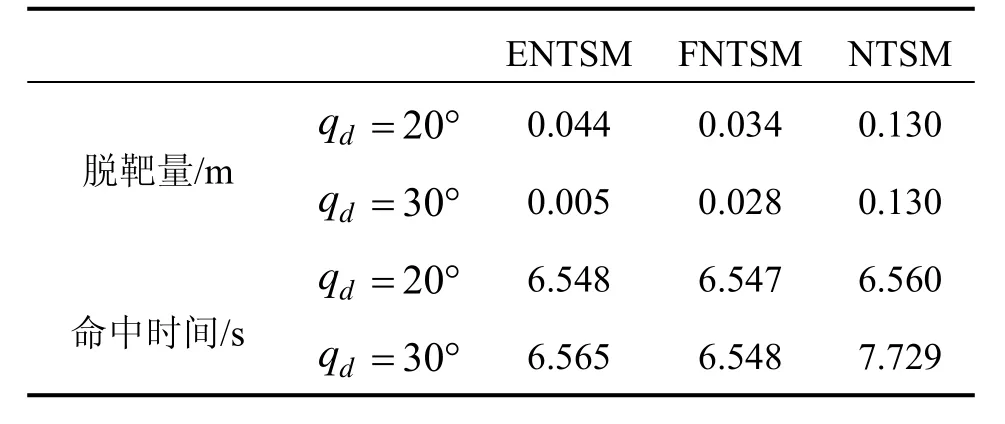
表1 余弦机动时的脱靶量和命中时间Tab.1 Miss-distances and interception times for consine maneuvering

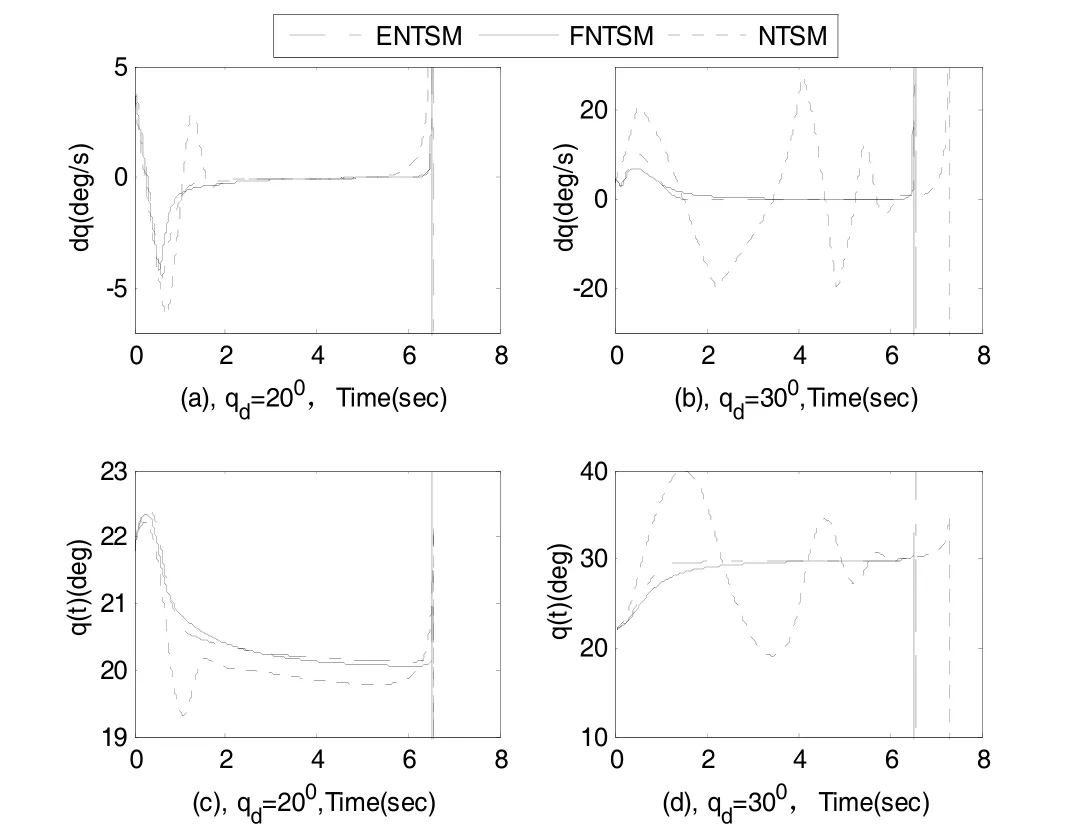
图2 视线角速率和视线角Fig.2 Line-of-sight angular rate and line-of-sight angle

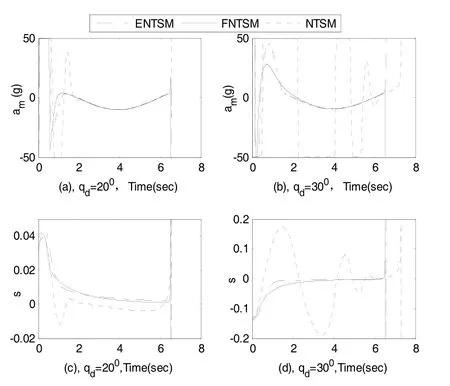
图3 导弹法向过载和滑模面Fig.3 Missile normal acceleration and sliding mode surface

进一步给出目标做阶跃机动时(情况 2)，三种方法的脱靶量和命中时间由表2给出，图4和图5分别给出相应的视线角速率、视线角、滑模面和导弹法向过载的变化曲线。

由表 2可见，当 qd=20°时脱靶量都很小，导弹命中时间也基本一致。但当 qd=30°时，ENTSM和NTSM导引律的脱靶量相近，而FNTSM的脱靶量和命中时间变化都不大。同样由图4和图5可见，方法NTSM 在 qd=30°时视线角速率和滑模面曲线振荡加剧，使得期望角误差变大，过载曲线饱和严重。而ENTSM和FNTSM方法在两种期望视线角情况下，都能使视线角速率和滑模面曲线收敛到零，过载曲线也快速的响应目标的阶跃机动，饱和时间短且在3 s后迅速稳定在一个定值。但FNTSM方法始终比ENTSM方法在制导精度上略胜一筹，这也体现了该方法选取的快速幂次趋近律的优越性。同时ENTSM和NTSM方法的制导精度与边界层参数的选取有关，过大过小都导致其性能变差。因此在收敛速度、抗外部扰动和内部参数摄动等方面，FNTSM方法更稳定强健。

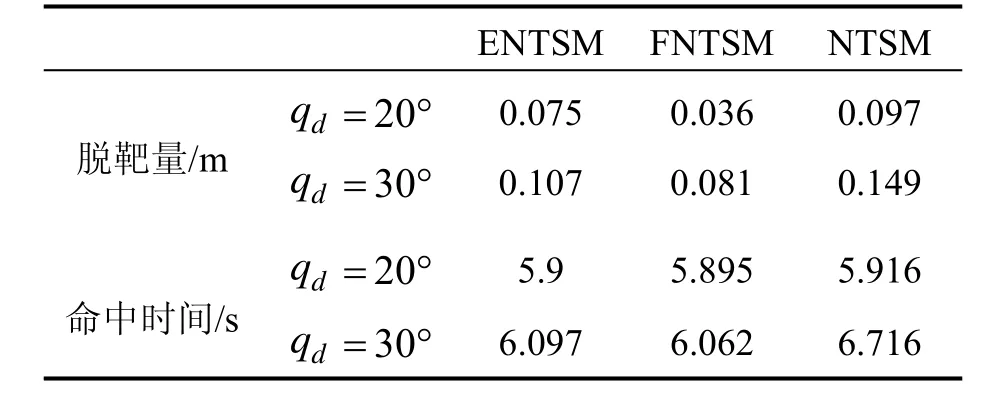
表2 阶跃机动时脱靶量和命中时间的对比Tab.2 Miss-distances and interception times

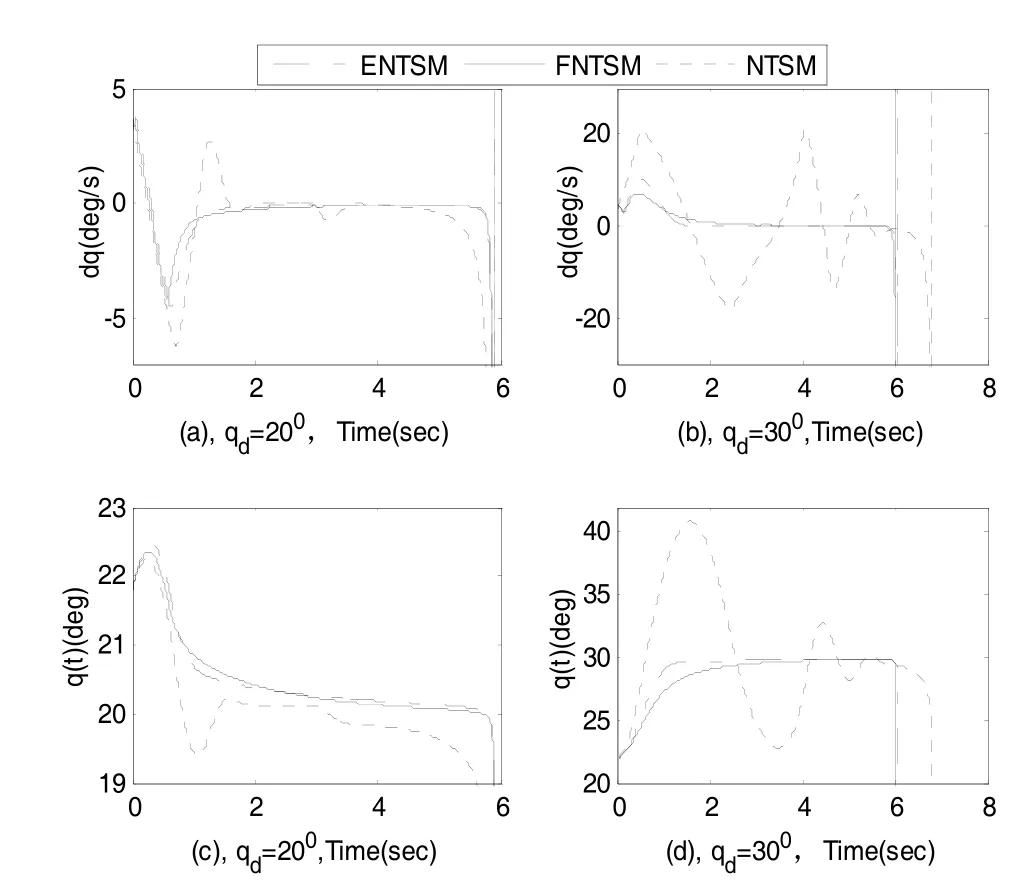
图4 视线角速率和视线角Fig.4 Line-of-sight angular rate and line-of-sight angle

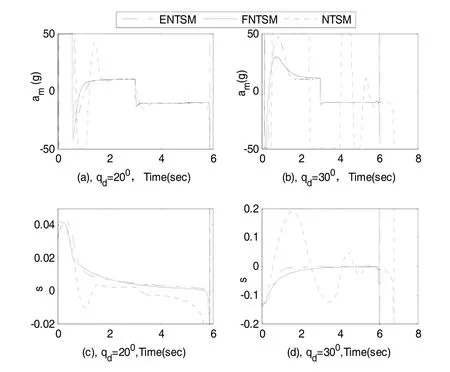
图5 导弹法向过载和滑模面Fig.5 Missile normal acceleration and sliding mode surface

对于目标做常值机动时的情况与前两种情况类似，限于篇幅不做进一步的讨论。文中所使用的扩张状态观测器只通过图 6给出目标做余弦机动时，ENTSM和FNTSM方法在两种期望视线角情况下的误差曲线图，可见在观测器的作用下，所用时间不到3s时，就可以快速、准确的跟踪到目标总扰动的值，相应误差曲线趋于零，体现了所选用观测器的实时有效性。其余情况类似不赘述。

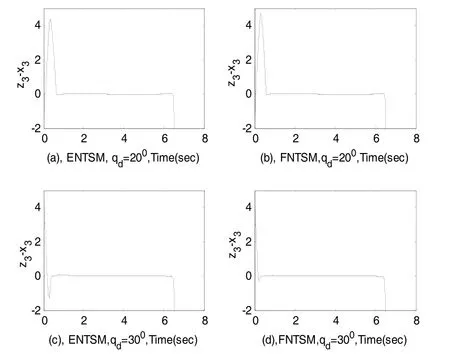
图6 余弦机动时的观测误差Fig.6 Observation error for consine maneuvering

4 结 论

运用指数趋近律和快速幂次趋近律，确保了系统到达滑模面的速度，结合非奇异终端滑模确保系统状态在有限时间内收敛到零，同时利用扩张状态观测器对系统状态和未知的目标扰动进行快速估计，设计了具有攻击角约束的导引律。针对不同的期望视线角和目标机动方式，与以往文献中已设计的传统非奇异终端滑模导引律比较，体现了本文所设计的两种导引律对于提高到达滑模面的速度和抑制滑模面抖动具有良好的性能和普适性。而运用扩张状态观测器估计目标加速度的方法具有算法简单、收敛速度快、估计精度高的优点，且无须建立机动目标模型，具有较好的工程应用前景。

（

）：

[1] 孙胜. 有限时间收敛寻的导引律[D]. 哈尔滨：哈尔滨工业大学，2010.

SUN Sheng. Guidance laws with finite time convergence for homing missiles[D]. Harbin: Harbin Institute of Technology, 2010.

[2] Kim M, Grider K V. Terminal guidance for impact attitude angle constrained flight trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, 9(5): 852-859.

[3] 王钊，李世华，费树岷. 非奇异终端滑模导引律[J].东南大学学报，2009，39(supⅠ)：87-90.

WANG Zhao, LI Shi-hua, FEI Shu-min. Nonsingular terminal sliding mode guidance law[J]. Journal of Southeast University, 2009, 39(supⅠ ): 87-90.

[4] Shima T. Intercept-angle guidance[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 484-493.

[5] Shashi R K, Sachit R, Debasish G. Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1230-1246.

[6] Sachit R, Debasish G. Terminal impact angle constrained guidance laws using variable structure systems theory[J]. IEEE Transactions on Control Systems Technology, 2013 (99): 1-10.

[7] 姚郁，王宇航. 基于扩张状态观测器的机动目标加速度估计[J]. 系统工程与电子技术，2009，31(11)：2682-2684+2692.

YAO Yu, WANG Yu-hang. Acceleration estimation of maneuvering targets based on extended state observer[J]. Systems Engineering and Electronics, 2009, 31(11): 2682-2684+2692.

[8] Zhu Z, Xu D, Liu J M, et al. Missile guidance law based on extended state observer[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5882-5891.

[9] Zhou D, Sun S, Teo K L. Guidance laws with finite time convergence[J]. Journal of guidance, control, and dynamics, 2009, 32(6): 1838-1846.

[10] Sun S, Zhou D, Hou W. A guidance law with finite time convergence accounting for autopilot lag[J]. Aerospace Science and Technology, 2013, 25(1): 132-137.

[11] 穆朝絮，余星火，孙长银. 非奇异终端滑模控制系统相轨迹和暂态分析[J]. 自 动 化 学 报，2013，39(6)： 902-908.

MU Chao-xu, YU Xing-huo, SUN Chang-yin. Phase trajectory and transient analysis for nonsingular terminal sliding mode control systems[J]. Acta Automatica Sinica, 2013, 39(6): 902-908.

[12] Feng Y, Yu X, Man Z. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167.

[13] Yu S H, Yu X H, Shirinzadeh B Y, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11): 1957-1964.

[14] 马克茂，贺风华，姚郁. 目标机动加速的估计与导引律实现[J]. 宇航学报，2009，30(6)：2213-2219.

MAO Ke-mao, HE Feng-hua, YAO Yu. Estimation of target maneuver acceleration and guidance law implementation in homing terminal guidance[J]. Journal of Astronautics, 2009, 30(6): 2213-2219.

[15] Hong Y G. Finite-time stabilization and stabilizability of a class of controllable systems[J]. Systems & Control Letters, 2002, 46(4): 231-236.

[16] Xia Y, Zhu Z, and Fu M, Back-stepping sliding mode control for missile systems based on an extended state observer[J]. IET control theory & applications, 2011, 5(1): 93-102.

Nonsingular terminal sliding mode guidance law with impact angle constraint

ZHOU Hui-bo1,2, SONG Shen-min1, LIU Hai-kun2
(1. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China; 2. School of Mathematical Sciences, Harbin Normal University, Harbin 150009, China)

In order to realize high-precision guidance when a missile intercepts high-speed maneuvering targets, the states in missile-target relative motion equations were extended in two-dimension plane, and an extended state observer was selected to implement motion compensation for the total disturbance that affects guidance performance. After that, two reaching laws were proposed based on a nonsingular terminal sliding mode surface, and two nonsingular terminal sliding-mode guidance laws with impact angle constraints were proposed. The numerical simulation demonstrate that, by using the observer to make real-time effective estimation for the extension of system state, the two designed guidance laws could meet the expected performance requirements, and the missiles could attack the targets quickly and precisely for different desired line-of sight angle and the manner of the target maneuver.

extended state observer; nonsingular terminal sliding mode surface; reaching law; finite time; guidance law

1005-6734(2014)05-0606-06

10.13695/j.cnki.12-1222/o3.2014.05.010

V448.133

A

2014-05-28；

2014-09-21

国家自然科学基金创新群体项目（61021002）；黑龙江省自然科学基金（A201111）

周慧波（1977—），女，博士研究生，研究方向为飞行器制导与控制。E-mail：zhouhb0306@sina.com

联 系 人：宋申民（1968—），男，教授，博士生导师，研究方向为非线性系统的稳定性分析、鲁棒控制、导弹制导与飞行器控制。E-mail：songshenmin@hit.edu.cn