基于EMD-FFT的水电机组振动信号检测

陈喜阳，闫海桥，孙建平

（华中科技大学能源与动力工程学院，湖北 武汉 430074）

0 引 言

水电机组设备在运行中不断受到机械或电气损伤，过流部件还经历空蚀破坏、泥沙磨损及尾水涡带、周期性脱流和卡门涡等水力激振力作用，振动信号可能是由机械、水力或电磁中的某一个因素产生的，也可能是由多个因素耦合作用引起的综合结果，体现出明显的非平稳特性[1-2]。为了对水电机组故障展开诊断，有必要提取与物理作用对应信号的动态特征，捕捉非平稳振动信号中与振源对应的突变成份时频征兆。当前水电机组振动信号分析方法依然立足于传统的FFT（快速傅立叶变换算法），从时域变换到频域时，丢失了时间信息，仅能求解到整体信号的频谱，无法确认各频率成份发生时刻，难以把握非平稳信号的局部细节信息，容易造成对机组实际运行性能的误判。

如何有效同时提取非平稳信号时域与频域特征，一直是信号处理领域的研究热点。Dennis Gabor提出了短时傅立叶变换,先用一个在有限区间外恒为零的光滑函数去乘所需分析的信号，再进行FFT，得到信号的局部特性，但所加窗口形状大小固定不变，使其在实际应用中受限制，效果不够理想[3]。EMD（empirical mode decomposition）经验模态分解作为一种自适应分解方法，在不同趋势或尺度上对原始信号逐层展开分解，衍生一序列的本征模函数（intrinsic mode function，IMF），通过对 IMF 分量进行Hilbert变换，获取该信号的时间-瞬时频率-瞬时幅值的特征分布[4]。EMD与传统FFT本质区别在于不需设定任何基函数，仅依据信号的局部特征尺度，自适应的对非平稳信号进行平稳化处理，已在旋转机械振动信号分析领域得到了应用。文献[4]对滚动轴承振动信号EMD分解，产生IMF分量，计算各IMF信息熵，设定熵阈值取舍IMF分量，对重构信号进行Hilbert包络谱分析，诊断实例验证该方法捕捉了轴承故障的特征频率。文献[5]将EMD分解后的IMF，进一步细分为包络和纯调频信号，然后对纯调频信号反余弦求取瞬时频率，获得了振动信号频率和幅值随时间动态变化趋势。文献[6]对水电机组摆度信号EMD分解产生的各IMF分量进行FFT，提取了摆度信号中蕴含的微弱涡带信息。文献[7]采用EMD与指标能量理论，提取了水电机组尾水管动态特征，可识别涡带是否发生及严重程度。EMD在上述应用实例中，均能有效捕捉到信号的时间信息以及频率信息，但由于缺乏严格的正交性，使得各IMF分量出现模态混淆现象，不同分量中通常包含频率相近的信号，导致分解结果的时间-瞬时频率-瞬时幅值中瞬时幅值出现失真而造成误判[8]。

针对上述状况，本文提出了一种融合FFT和EMD经验模态分解的EMD-FFT时频分析方法，算法思想为:利用EMD时频聚焦性，自适应的将原始信号进行平稳化分解，从IMF分量中捕获非平稳信号的突变成份发生时段，并通过FFT获得该时段原始信号的频率与幅值信息，准确获取了非平稳信号的时间-瞬时频率-瞬时幅值。仿真算例和水电机组振动分析实例表明，EMD-FFT克服了FFT丢失了时间信息和EMD中所得幅值信息不准的缺陷，可有效的捕捉突变信号的时间-瞬时频率-瞬时幅值特征量，为水电机组非平稳振动信号检测提供了一种新时频分析方法。

1 EMD-FFT时频分析方法

EMD-FFT根据非平稳信号自身的局部时间特征尺度，自适应按照频率从高到低分解为若干IMF本征模函数序列，实现了非平稳信号在不同尺度或趋势上的平稳化处理过程，捕捉突变信号发生时刻，并对该时段的原始信号进行FFT分析，最终检测到该非平稳信号的时间-瞬时频率-瞬时幅值特征量。EMD-FFT实质是利用EMD经验模态分解精准地捕获突变信号的时域信息，并结合FFT获取频率及幅值信息，算法流程如下:

（1）计算原始信号x（t）所有极大值点和极小值点。

（2）运用三次样条曲线插值拟合出x（t）的上、下两条包络曲线。

（3）求取x（t）上、下包络线的均值，记为μ，然后用 x（t）减去 μ，得到剩余分量 h（t）=x（t）-μ。

（4）判断h（t）是否满足IMF的两个条件:在所有的数据序列中，极值点的个数与过零点的个数相等或者最多相差一个；所有的极大值点确定的上包络线与所有的极小值点确定的下包络线的平均值为零。若h（t）不满足IMF条件，将其作为原始数据即x（t）=h（t），重复以上步骤 （1） 到 （4），直到得到一个IMF； 否则，将h （t）作为x（t）的一个IMF分量，即 c（t）=h（t）。

（5） 将 c（t）从 x（t）中分离出来，得到的剩余分量 r（t）作为原始数据，重复以上步骤（1）到（5），直到r（t）只有一个极值点为止，此时r（t）为残余分量。

（6） 原始信号通过上述（1）到（5）变换后，实现了非平稳信号在不同频率或趋势上的平稳化处理过程，绘制所有的IMF波形图，确定突变信号成份所对应的时段，获取该突变信号时间信息。

（7）通过FFT计算该时段原始信号的频率与幅值信息，综合EMD所获得的时间信息，最终提取非平稳信号的时间-瞬时频率-瞬时幅值特征量。

2 仿真算例

为了验证EMD-FFT在检测非平稳信号动态特性的效果，下面以一个仿真的振动信号为例，说明EMD-FFT时频分析的具体实施过程，并与单一的FFT分析及EMD分析结果对比。仿真信号解析表达式为:

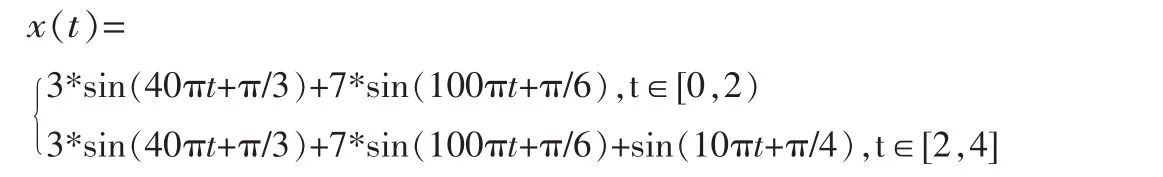
由表达式可知，仿真信号在0～4 s时间范围内主要由20、50 Hz两个标准的正弦信号组成，从2 s时刻开始另叠加一个5 Hz的正弦信号。分别采用传统的FFT、EMD和EMD-FFT对仿真信号展开分析。

FFT对原始信号在0～4 s时域上的分析如图1所示。由图1可以看出:原始波形时域图上无法准确划分叠加的5 Hz正弦信号的具体时刻；频谱图清晰描绘出仿真信号在0～4s时间存在3种频率信号，分别为20、50 Hz和5 Hz，但丢失了各频率成份信号作用的时间信息；FFT计算结果还显示20 Hz频率信号对应的幅值为3，50 Hz频率信号对应的幅值为7，5 Hz频率信号对应的幅值为0.5，其中50 Hz和20 Hz两个频率成分的幅值与仿真信号对应频率的幅值一致，但是5 Hz频率成分的幅值却与实际的不同，出现了衰减，传统的FFT无法准确提取仿真信号中各频率成份的幅值。

图1 原始仿真信号时域波形及频谱

单一FFT分析结果表明，频谱分析方法仅能获取信号整体时域的频谱信息，无法提供各频率成份作用的时间信息，特别针对非平稳信号，还难以有效提取突变信号成份的幅值信息。

EMD分解建立在信号自身的时间尺度特征上，无需预先设定任何先验性的基函数，在非平稳信号分析方面具有一定特色，对仿真信号的经验模态分解产生的各IMF及其频谱分析如图2和3所示:EMD按照不同趋势或尺度，自适应的分解产生一序列IMF，各阶IMF分量包含了原仿真信号的不同时间尺度的局部特征信号，随着分解层数的增加，IMF的频率越来越低；1IMF和2IMF的波形持续在整个时间段内，1IMF频率与幅值为50.02 Hz和6.995，2IMF频率与幅值为20.01Hz和2.888，与仿真信号中的50 Hz和20 Hz信号特征基本一致；3IMF的波形表明该尺度信号仅在虚线圈区域存在，在2 s时刻左右叠加进来的突变信号成份，3IMF频率及幅值为5.002 Hz和0.463。

EMD分析结果揭示，经验模态分解可相对准确的划分各频率成份信号的发生时刻，捕捉突变信号的时间信息及频率信息，但所获取的突变信号的幅值有较大程度衰减，这主要由于EMD分解原理缺乏严格正交性制约，导致相近频率信号分布到不同IMF分量而造成的幅值失真。

FFT能提取待分析时段信号的频谱信息，仅当该频率成份为相对稳定信号时，所提取的幅值信息才比较准确，而EMD可将非平稳信号进行平稳化处理，能有效划分突变信号作用的时间区域。本文所构建的EMD-FFT通过经验模态分解，划分突变信号的作用时间，对该时段的原始信号展开FFT分析，获取该突变成份的时间-频率-幅值特征。图4所示的EMD-FFT时频分析结果表明: 5.005 Hz突变信号作用时间域为2～4 s，幅值为1.004，与仿真信号接近，50 Hz和20 Hz作用于整个0～4 s的幅值也与仿真信号保持一致。

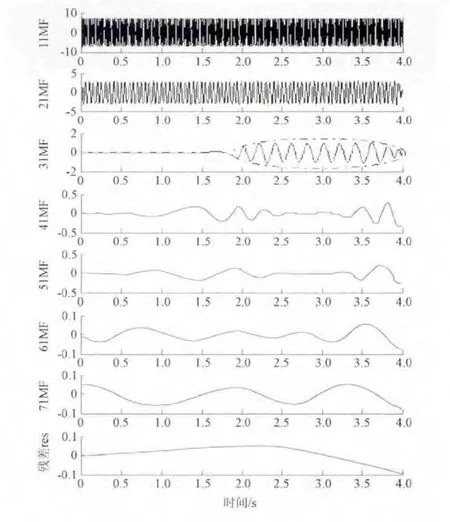
图2 原始仿真信号EMD分解

图3 各阶IMF频谱

图4 突变信号 （2～4 s）时域波形及频谱图

对照FFT、EMD和EMD-FFT分析结果可知，EMD-FFT可作为一种有效的动态信号检测手段，克服了传统FFT分析存在丢失时间信息和EMD提取的突变信号幅值衰减的缺陷，能相对精准捕捉突变信号的时间-频率-幅值特征。

3 EMD-FFT应用于水电机组非平稳信号的征兆提取

下面结合某水电厂机组 （额定转速为75 r/min，转频为1.25 Hz）连续升负荷试验的下导摆度Y信号，采用EMD-FFT时频分析，提取突变信号部分的时频特征。原始信号采样频率为1024 Hz，采样点数据长度为159744点，为了便于计算，这里首先对该信号进行32抽1的重新采样，则采样频率调整为32 Hz，重新采样后时域波形如图5。

图5 下导摆度Y时域波形

由图5可以看出，水电机组作为涉及水、机、电的大型复杂系统，影响运行因素众多，连续升负荷过程中的下导摆度Y信号体现出较强的非平稳特征，某负荷区域振动强烈，发生突变。按照EMDFFT时频分析流程，首先借助EMD经验模态分解，从各IMF分量时域波形 （如图6）中，可观察到突变分量主要集中分布到5IMF和6IMF中，确定突变成份作用时间区域为60～100 s之间，提取该时间区域的Y信号，展开FFT分析，获取该突变信号成份频谱特征见表1（仅给出前8位的频率和幅值）。

图6 突变信号 （60～100 s）时域波形图及频谱

表1 变负荷过程中下导摆度Y突变成份频谱分析结果

由水轮机工作原理可知，机组在特定负荷区间运行时，尾水管内会形成强制旋涡或旋转涡带，引发较强低频压力脉动，该脉动频率一般为1/6～1/2转频。EMD-FFT所提取的突变信号发生在60～100s之间，主要频率为0.25～0.35 Hz之间，机组负荷为388-465 MW，处于涡带工况，突变信号是由尾水涡带引起，该方法有效捕捉到变负荷过程中下导摆度Y突变成份的时间-频率-幅值特征。EMD-FFT提取的突变信号频率分布在0.25～0.35 Hz之间，原因可能有二:一是FFT分析存在能量泄漏；二是连续变负荷，水力因素造成的低频振动强度和频率在时间域上本身就具有一定差异。

4 结 论

针对FFT和EMD在非平稳信号分析时存在一定缺陷，综合两者优势，构建了一种EMD-FFT的信号时频分析方法。EMD-FFT通过EMD分解，自适应地将非平稳原始信号进行平稳化处理，确定突变成份发生时刻，利用FFT对EMD确定的时段内信号频谱分析，最终获得突变信号的时间-频率-幅值特征。仿真结果表明，EMD-FFT克服了FFT丢失时间信息和EMD幅值衰减的缺陷，为非平稳信号中突变成份的动态检测提供了一种新手段，并应用到水电机组连续变负荷过程中，成功捕捉了下导摆度Y信号中因尾水涡带导致低频突变信号成份的时间-频率-幅值信息。

［1］王恒超，陈喜阳，何志锋.基于插值重采样的信号FFT分析方法研究［J］.水力发电，2012，38（3）:21-23.

［2］张梦禾，陈喜阳，张润时.三峡左岸6号机组振动分析及量化征兆提取策略［J］.水力发电，2012，38（4）:24-27.

［3］陈喜阳.水电机组稳定性监测中状态分析方法研究［D］.南京:南京南瑞集团，2008.

［4］朱瑜，王殿，王海洋.基于EMD和信息熵的滚动轴承故障诊断［J］.轴承，2012（6） :50-53.

［5］胡劲松，杨世锡，任达千.一种基于EMD的振动信号时频分析新方法研究［J］.振动与冲击，2008，27（8）:71-73，154，178.

［6］司青花，王瀚，何苗，等.EMD谱方法提取水轮机动态特征信息［J］.大电机技术，2011（6） :56-59.

［7］王瀚，罗兴锜，薛延刚，等.EMD指标能量提取水轮机尾水管动态特征信息［J］.水力发电学报.2012，31（5）:286-290.

［8］胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题［J］.振动、测试与诊断，2011，31（4）:429-434，532.