粗粒料二维与三维孔隙率的对应关系研究

何咏睿 ，朱 晟 ，2，武利强 ，2

（1.河海大学水工结构研究所，江苏 南京 210098；2.河海大学水文水资源与水利水电工程科学国家重点实验室，江苏 南京 210098）

0 引 言

近年来我国高土石坝发展十分迅速，粗粒料作为土石坝的主要材料，其力学特性对坝体的变形有着决定性的影响。对粗粒料进行二维数值试验时，孔隙率是影响粗粒料力学性质的重要因素，对粗粒料的强度与变形均有很大的影响。为使二维数值试验中的二维模型与模拟的三维实体力学性质等价，必须实现二维模型的孔隙率与三维实体的等价。现今常用的二维与三维孔隙率转换公式是由等粒径颗粒体组成的结构推导而出，仅用密实度进行修正，未考虑粒径分布对孔隙率的影响[1-3]，无法实现二维模型孔隙率和实体的三维孔隙率完全等价。鉴于此，本文参考不同土石坝工程的粗粒料级配，设计一系列具有代表性的级配组，对每组用二维颗粒流程序（pfc2d）和三维颗粒流程序 （pfc3d）模拟极值孔隙率试验，统计出不同级配下二维与三维极值孔隙率，探讨粒径分布及压实程度对二维与三维孔隙率转换关系的影响，拟合出二维与三维孔隙率的转换公式，并与常用的转换公式进行比较。

1 数值试验的级配确定

土石坝为当地材料坝，受料场原生条件的限制，不同工程所用粗粒料级配差异较大。为了使所选用的级配曲线组具有代表性，探寻不同工程粗粒料级配的共有特征，在采用重型振动碾进行薄层碾压施工的工程中，粗粒料的级配设计均以talbot曲线[4]为母线。

参照水布垭和三板溪[5-6]等工程级配设计方法，以talbot曲线为母线设计试验级配。根据DL/T 5356—2006《水利水电工程粗粒土试验规程》，选定最大粒径为60 mm，引入分形维数定义talbot曲线形状指数[7]，设置分形维数n分别为2.7、2.6、2.5、2.4、2.3、2.2、2.1、2.0，所得的级配曲线组见图1。曲线组构成的区域几乎涵盖现代采用连续级配理论设计的堆石坝进行数值试验的级配。因此，根据这组级配研究得到的规律适用于现代及今后按连续级配理论设计的堆石坝粗粒料的数值试验研究中。

图1 各分形维数下的级配

2 数值试验

2.1 颗粒流程序模拟粗粒料极值孔隙率试验的可行性分析

由等粒径颗粒结构推导出的常用二维与三维孔隙率转换关系为[3]

式中，ε2d为二维孔隙率；ε3d为三维孔隙率；ξ为修正系数；Dr为相对密度。

用pfc2d和pfc3d模拟等粒径颗粒料的极值孔隙率试验，校验得出的二维与三维孔隙率是否符合公式（1），以此决定研究方案的可行性。为加快计算速度，pfc2d数值模拟中设置颗粒直径为0.005 m、2000个；pfc3d中设置颗粒直径为0.005 m、5000个。将pfc2d模拟极值孔隙率试验后得出的极值孔隙率按公式（1）转换成三维孔隙率，与pfc2d、pfc3d模拟极值孔隙率试验得到的极值孔隙率统计于表1。表1中，按公式转换得到的三维孔隙率与pfc3d模拟得到的孔隙率非常近似，证明用颗粒流程序模拟极值孔隙率试验探究二维与三维孔隙率转换关系的方案可行。

表1 等粒径颗粒组的二维、三维极值孔隙率

2.2 pfc模拟极值孔隙率试验

2.2.1 试验参数的确定

数值试验参数通过一组硅质岩堆石料三轴试验曲线反算调整获得[8-9]，数值试验的细观参数见表2。其中，Kn、Ks分别为颗粒的法向及切向接触刚度；f为颗粒间摩擦系数。

表2 数值试验的细观参数

2.2.2 数值模拟步骤

（1）建立边界:在pfc3d中建立底半径为0.15 m，高为0.34 m的圆筒模型。在pfc2d中建立宽为0.3 m、高为0.34 m的矩形模型。

（2）制样:在边界中根据设计的级配曲线制样，按照水利水电实验规程，粗粒料按60～40、40～20、20～10、10～5 mm以及5 mm以下进行粒组筛分，但依此生成颗粒后发现pfc3d中颗粒数目达几十万个，远远超出电脑负荷。因此，将5 mm以下的颗粒全部用5～10 mm颗粒进行等质量替换。

（3）模拟松填法求最大孔隙率:颗粒在重力作用下自由下落，通过控制颗粒速度确保颗粒落距2～5 cm，颗粒下落稳定后为最大孔隙率状态。

（4）模拟振动台法求最小孔隙率:在颗粒表面置加重底板，使其对颗粒产生14 kPa的平均压力。设定底部墙体运动方程为正弦曲线，振幅为0.002 m，频率为251.3 rad/s，模拟振动台振动，追踪配位数变化，稳定后停止振动，颗粒达到最密实状态。

（5）卸除加重底板，颗粒释放应力自由回弹后为最小孔隙率状态。

2.2.3 模拟结果

根据公式（1），将pfc2d数值模拟得到的孔隙率换算成三维孔隙率，与pfc2d、pfc3d模拟得到的极值孔隙率统计于表3。

3 结果分析

3.1 数据有效性分析

从表3看出，三维孔隙率均大于二维孔隙率，这是由于二维模型中假定所有的颗粒球心均处在一个平面上，而实际三维实体中颗粒球心无规律分布于空间，更容易形成 “弓形”架构。

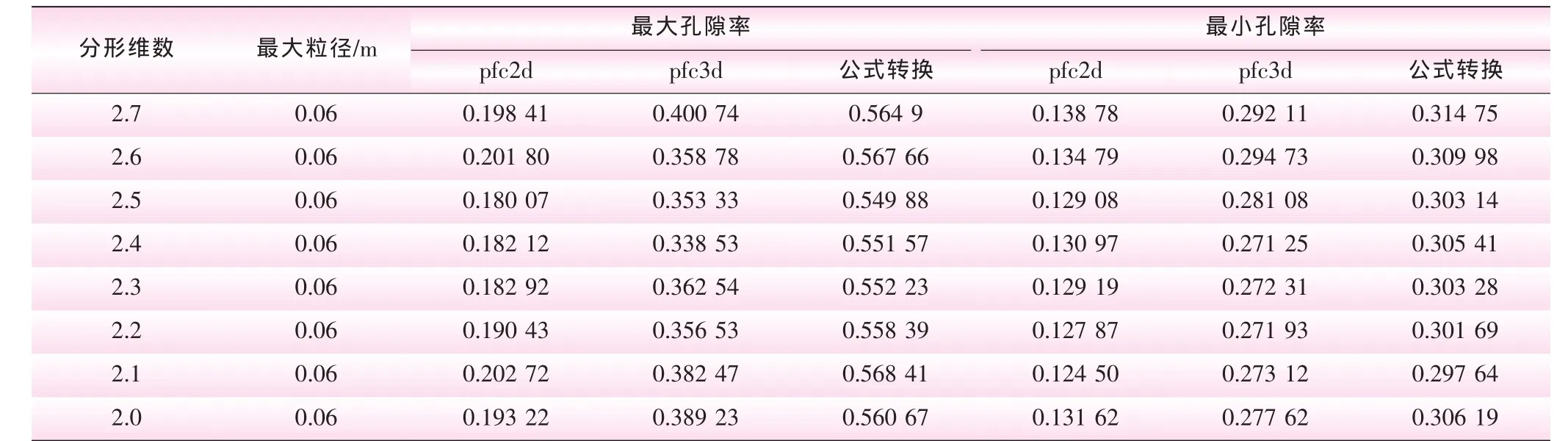
表3 各级配的极值孔隙率

由于pfc3d运算对颗粒数目的限制，制样中简化了0～5 mm的颗粒，不可避免地给极值孔隙率值带来一定误差。表3中，分形维数由2.7减至2.0，极值孔隙率总体上呈先减后增的趋势，在分形维数为2.5左右达到最小，这与Ochiai M等[10]得到的规律相吻合。本文旨在探究粗粒料的二维与三维极值孔隙率转换关系，pfc2d与pfc3d数值试验中粗粒料级配的简化是同步的，且所得数据符合实际规律，故得到的转换关系是可靠的。

3.2 拟合公式

绘制pfc数值试验得到的三维孔隙率关于二维孔隙率的散点图 （见图2），将二维极值孔隙率按公式 （1）换算得到三维孔隙率，在图2中绘入公式换算得到的三维孔隙率与二维孔隙率对应点。图2中，按照公式换算得到的三维孔隙率较pfc3d模拟得到的均偏大，且在Dr=0.0时相差较大。这是由于公式 （1）由等粒径颗粒体推导而来，仅用相对密度进行修正，忽略了粒径分布对孔隙率的影响，而级配良好的颗粒堆积体孔隙率明显小于级配差的，故按照公式计算的孔隙率均大于pfc3d模拟得到的。

对不同分形维数下二维与三维极值孔隙率进行相关性分析可知，二维与三维极值孔隙率呈高度线性相关，相关系数达0.94，可用直线y=1.4618x+0.08794拟合，并绘制拟合直线于图2中。显然，相比于公式 （1），该直线能更好地反应粗粒料二维与三维极值孔隙率的关系，且相对密度分别为0.0与1.0时，二维与三维孔隙率的对应点分别密集分布在直线的 x=0.12～0.14、0.18～0.20段。由此推测，其他相对密度下粗粒料二维与三维孔隙率对应点会密集分布在0.14～0.18段，但需进一步证实。

图2 二维与三维孔隙率对应点

4 结 论

通过设计一系列具有代表性的粗粒料级配，用pfc2d、pfc3d模拟极值孔隙率试验探究粗粒料二维与三维孔隙率的对应关系，得出如下结论:

（1）实际三维结构比二维模型的孔隙率大。二维模型假定所有的颗粒球心均处在一个平面上，而三维结构中颗粒球心无规律分布于空间中，更易形成 “弓形”架构，故孔隙更大。

（2）相同压实度下，等粒径颗粒体比级配良好的颗粒体的孔隙率大。根据常用二维与三维孔隙率转换公式求得的三维孔隙率会大于实际三维孔隙率，且在相对密度为0时相差较大。

（3）设计级配下，粗粒料的二维极值孔隙率与三维极值孔隙率呈高度线性相关，用直线拟合后具有良好的归一性。相对密度分别为0.0与1.0时，二维与三维孔隙率的对应点分别密集分布在直线的两段，推测其他密实度下二维与三维孔隙率对应点也会密集分布在该直线的某段，但需进一步研究证实。

（4）本次数值试验探究粗粒料的二维与三维孔隙率对应关系，没有考虑粗粒料的颗粒形状和破碎的影响，考虑颗粒形状和破碎后粗粒料的二维与三维孔隙率对应关系尚待进一步探究。

［1］MITCHEL J K.岩土工程土性分析原理［M］.高国瑞，译.南京:南京工学院出版社，1988.

［2］日本土质工学会.粗粒料的现场压实［M］.北京:水利水电出版社，1999.

［3］张刚.管涌现象细观机理的模型试验与颗粒流数值模拟研究［D］.上海:同济大学，2007.

［4］王永明，朱晟，任金明，等.筑坝粗粒料力学特性的缩尺效应研究［J］.岩土力学，2013，34（6）:1799-1807.

［5］李昌彩.水布垭面板堆石坝前期关键技术研究［M］.北京:水利水电出版社，2005.

［6］赵海斌.超硬岩筑坝材料现场爆破与现场碾压试验研究［R］.长沙:中国水电顾问集团中南勘测设计研究院，2006.

［7］朱晟，武利强，魏匡民，等.一种基于分形理论的粗粒料缩尺方法: 中国，CN103134906A［P］.2013-06-05.

［8］王永明，任金明，武利强，等.pfc模拟筑坝粗粒料力学特性的有效性分析［J］.水电能源科学，2012，30（10）:72-75.

［9］周健，池毓蔚，池永，等.砂土双轴试验的颗粒流模拟［J］.岩土工程学报，2000，22（6）:701-704.

［10］OCHIAI M,OZAO R,YAMAZAKI Y,et al.Self-similarity law of particle size distribution and energy law in size reduction of solids［J］.Physica A:Statistical Mechanics and its Applications,1992,191（2）:295-300.